UNIT 2
Partial differentiation
Question-1: Find all the second order partial derivative;
z = x cos y – y cos x
Solution: here, first we will find first order derivative,
 = cos y + y sin x ,
= cos y + y sin x , 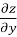 = - x sin y – cos x
= - x sin y – cos x
Now,
 =
= 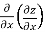 =
=  ) = y cos x
) = y cos x
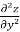 =
=  =
= 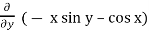 = - x cos y
= - x cos y
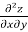 =
= 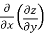 =
= 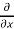 (- x sin y – cos x) = - sin y + sin x
(- x sin y – cos x) = - sin y + sin x
 =
= 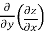 =
= 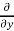 (cos y + y sin x ) = - sin y + sin x
(cos y + y sin x ) = - sin y + sin x
Here we notice,  =
= 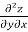
Question-2: Find all of the second partial derivatives of the function:
f( x, y, z) = 3x³ 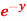 sin z
sin z
Solution: We notice here that, the function has three variables,
Now first we will find all of the first order partial derivatives ,
 = 9x²
= 9x²  sin z ,
sin z , 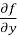 = - 3x³
= - 3x³ 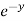 sin z ,
sin z , 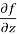 = 3x³
= 3x³  cos z
cos z
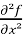 =
= 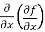 =
= 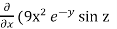 ) = 18 x²
) = 18 x²  sin z
sin z
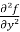 =
=  =
=  = 3x³
= 3x³ 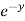 sin z
sin z
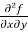 =
= 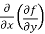 =
= 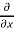 (
(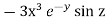 ) =
) = 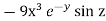
 =
=  =
= 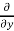 (9x²
(9x²  sin z ) = - 9x²
sin z ) = - 9x²  sin z
sin z
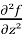 =
= 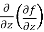 =
=  3x³
3x³  cos z) = - 3x³
cos z) = - 3x³ 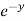 sin z
sin z
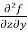 =
= 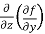 =
= 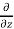 (- 3x³
(- 3x³ 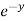 sin z ) = - 3x³
sin z ) = - 3x³ 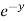 cos z
cos z
 =
=  =
=  (9x²
(9x²  sin z) = 9x²
sin z) = 9x² 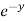 cos z
cos z
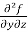 =
= 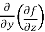 =
= 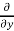 (3x³
(3x³ 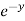 cos z) = - 3x³
cos z) = - 3x³ 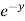 cos z
cos z
 =
=  =
= 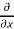 (3x³
(3x³ 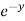 cos z) = 9x³
cos z) = 9x³ 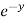 cos z)
cos z)
Question-3: Verify Euler’s theorem for the following function:
u = x³ + y³ + 3 xy²
Solution: Here u is homogeneous function of degree 3.
To verify,
x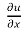 + y
+ y  = nu
= nu
Here,
u = x³ + y³ + 3xy²
Differentiating partially with respect to x, we get
 = 3x² + 0 + 3y² = 3x² + 3y²
= 3x² + 0 + 3y² = 3x² + 3y²
Or x  = 3x³ + 3xy² ----------------------- (1)
= 3x³ + 3xy² ----------------------- (1)
Now , differentiating partially with respect to y, we get
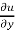 = 0 + 3y² + 6xy
= 0 + 3y² + 6xy
Or y 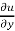 = 3y³ + 6xy² ---------------------------(2)
= 3y³ + 6xy² ---------------------------(2)
Adding equation (1) and (2), we get
x 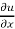 + y
+ y 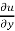 = 3x³ + 3xy² + 3y³ + 6xy²
= 3x³ + 3xy² + 3y³ + 6xy²
= 3x³ + 3y³ + 9xy²
= 3( x³ + y³ + 3xy² )
x  + y
+ y 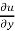 = 3u
= 3u
Hence Euler’s theorem is verified.
Question-4: If u = log ( x³ + y³ + z³ - 3xyz) , then show that

Solution: here , log ( x³ + y³ + z³ - 3xyz)
Differentiate it partially with respect to x, we get


Similarly,
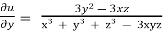 ,
,
And
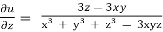
Now adding all these results,


= 
= 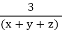
Now we will perform following steps in order to get the result,
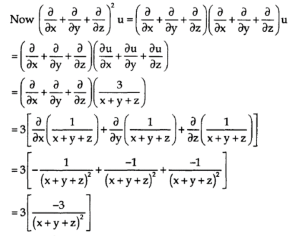
= 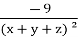
Question-5: If u = 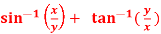 , show that,
, show that,
x 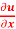 + y
+ y 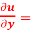 0
0
Solution : here, differentiate u partially with respect to x,
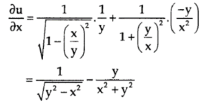
Or,
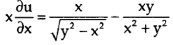
Now partially differentiate w.r.t y,
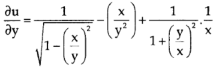
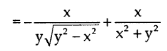
y  =
= 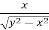 +
+ 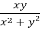
By adding, we get
x  + y
+ y  0 hence proved.
0 hence proved.
Question-6: if ,
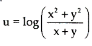
Prove that - x  + y
+ y 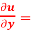 1
1
Solution: we are given,
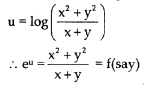
Here f is a homogeneous function of degree 1,
By Euler’s theorem,

Or x 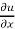 + y
+ y  1. Hence proved.
1. Hence proved.
Question-7: If,
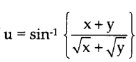
Then prove that , x 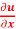 + y
+ y 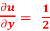 tan u
tan u
Solution: it is given that,
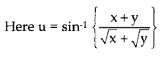
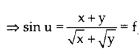
Here f is a homogeneous function of degree ½
By using Euler’s theorem,
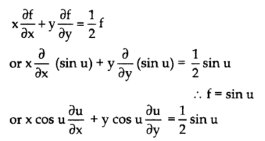
So, x 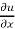 + y
+ y 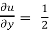 tan u. hence proved.
tan u. hence proved.
Question-8: if u = 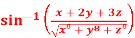 , show that
, show that
, x 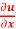 + y
+ y 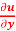 + z
+ z 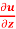 + 3 tan u = 0.
+ 3 tan u = 0.
Solution: it is given that, u = 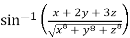
Sin u = 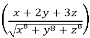 = f
= f
Here f is a homogeneous function ,
By Euler’s theorem,
x 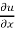 + y
+ y 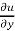 + z
+ z 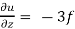
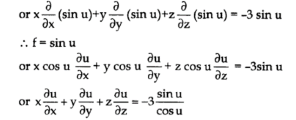
So that,
x  + y
+ y 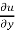 + z
+ z  + 3 tan u = 0 hence proved.
+ 3 tan u = 0 hence proved.
Question– 9: if ∅( x , y, z) = 0, then show that,
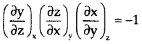
Solution: here first we treat x as constant, we get
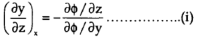
Now we treat y as constant,
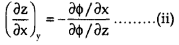
Similarly,
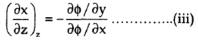
By multiplying equation (1) , (2), and (3), we get
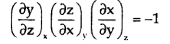
Hence proved.
Question-10: if u = u(y –z, z – x, x – y)
Prove that, x  + y
+ y 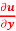 + z
+ z 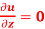
Solution : here , u = u(y –z, z – x, x – y)
Suppose, X = y-z , Y = z-x, Z = x-y ………………………. (i)
So, u = u(X , Y , Z)
Now,
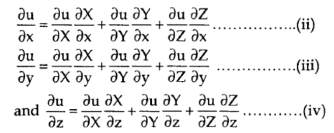
With the help of (i), (ii), (iii) (iv) gives,
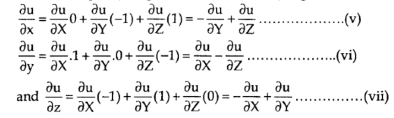
Adding (v) , (vi) and (vii), we get,
x 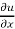 + y
+ y 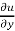 + z
+ z 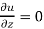
Hence proved.