UNIT-2

PARTIAL DIFFERENTIATION 1

Q 1: If . Then prove that

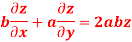
Given 

   Partially differentiating z with respect to x keeping y as constant

Again partially differentiating given z with respect to y keeping x as constant

On b.eq(i) +a.eq(ii) we get

Hence proved.

Q 2: If Show that

Given 

 Partially differentiating z with respect to x keeping y as constant

Again partially differentiating z with respect to x keeping y as constant

Partially differentiating z with respect to y keeping x as constant

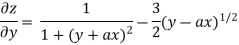
 Again partially differentiating z with respect to y keeping x as constant

From eq(i) and eq(ii) we conclude that

Q 3  : Find the value of n so that the equation

Satisfies the relation 

Given   

  Partially differentiating V with respect to r keeping as constant

 Again partially differentiating given V with respect to keeping r as constant

Now, we are taking the given relation

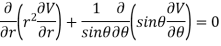
Substituting values using eq(i) and eq(ii)

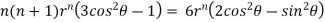
On solving we get 

Q 4 : If then show that when

Given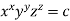 

Taking log on both side we get

Partially differentiating with respect to x we get

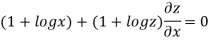
…..(i)

         Similarly partially differentiating with respect y we get

……(ii)

LHS 

Substituting value from (ii)

   Again substituting value from (i) we get

.()                

When

=RHS

Hence proved

Q 5 :If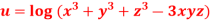

Then show that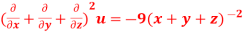 

Given 

Partially differentiating u with respect to x keeping y and z as constant

Similarly paritially differentiating u with respect to y keeping x and z as constant

  …….(ii)

  ……..(iii)

LHS: 

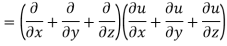
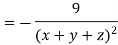
Hence proved

Q 6: Show that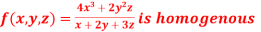

Given

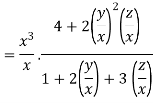
Therefore f(x,y,z) is an homogenous equation of degree 2 in x, y and z

Q 7: If

Let

Thus u is an homogenous function of degree 2 in x and y

Therefore by Euler’s theorem

substituting the value of u

Hence proved

Q 8: If , find the value of

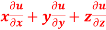
Given 

Thus u is an homogenous function of degree 6 in x ,y and z

Therefore by Euler’s theorem

Q 9: If 

Given 

Thus u is an homogenous equation of degree -1 in x and y

Therefore by Euler’s theorem

Q 10: Solve the following using chain Rule

Y=

Solution:

Then ,

Substituting U = in the above we have

Q 11:

There really isn’t all that much to do here other than using the formula

So, technically we’ve computed the derivative. However,we should probably go ahead and substitute in for x and y as well doing this gives