UNIT-3
PARTIAL DIFFERENTIATION 2
Q 1: Let x(u,v) = u2 – v2, y(u,v)=uv.find the jacobain j(u,v).
Solution:
Given that x(u,v) =u2-v2 and y(u,v)= 2uv
We know that,
J(u,v)= 
Therefore, J(u,v) = 4u2+4v2
Q 2: Find  if u= 2xy, v= x2 – y2 and x = r.cos
if u= 2xy, v= x2 – y2 and x = r.cos , y = r.sin
, y = r.sin
Solution:


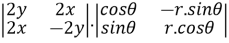
= 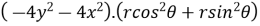
= 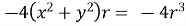
Q 3: Expand in power of
in power of  up to second terms.
up to second terms.
Given function 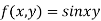
Here 
Now, 


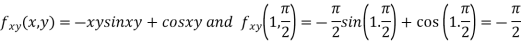
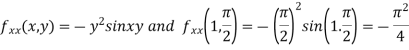
 and
and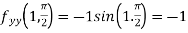
The Taylor’s expansion in power  is
is
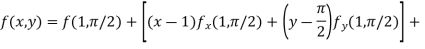




Q 4: Expand the  in power of x and y up to third term?
in power of x and y up to third term?
Given function 
Now, 









By Maclaurins expansion
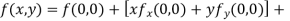

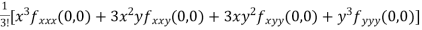 +…
+…


Q 5: Let z = f(x, y)
A5)
Now for stationary point dz = 0
 &
&
This gives the set of values of x and y for which maxima or minim occurs
Now find 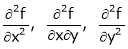
We called it as r, s, t resp.
Thus function has maximum or minimum
ifrt – s2>0
i.e. 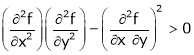
further if

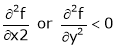
Q6: Decampere a positive number ‘a’ in to three parts, so their product is maximum
A6)
Let x, y, z be the three parts of ‘a’ then we get.
 … (1)
… (1)
Here we have to maximize the product
i.e. 
 By Lagrange’s undetermined multiplier, we get,
By Lagrange’s undetermined multiplier, we get,

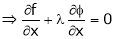 … (2)
… (2)
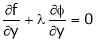 … (3)
… (3)
 … (4)
… (4)
i.e.
 … (2)’
… (2)’
 … (3)’
… (3)’
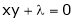 … (4)
… (4)



And 

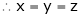
From (1)



Thus 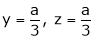 .
.
Hence their maximum product is  .
.
Q 7: Find the point on plane  nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
A7) Let  be the point on sphere
be the point on sphere 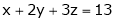 which is nearest to the point
which is nearest to the point 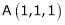 . Then shortest distance.
. Then shortest distance.
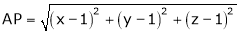

 Let
Let 
Under the condition  … (1)
… (1)
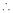 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have

 … (2)
… (2)

 … (3)
… (3)
i.e.  &
&

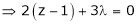 … (4)
… (4)
From (2) we get 
From (3) we get 
From (4) we get 
 Equation (1) becomes
Equation (1) becomes
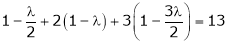
i.e. 
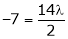


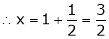
y = 2

If 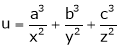 where x + y + z = 1.
where x + y + z = 1.