Unit – 4

INTEGRAL CALCULUS

Q 1: Find the value of 1/2 ?

Solution:

Let

Then

When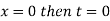

And then t=

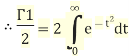
Squaring both sides we get

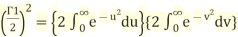where u and v is any variable in place of t.

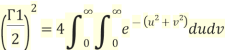
   Converting it in polar co-ordinates

  Since 

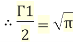
Q2:

By the definition of gamma function we know that

Putting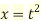

Then

When then

then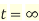

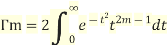
Similarly

So,  ()(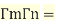

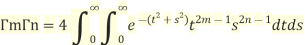
Converting into polar co-ordinates

Let

Also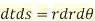

Where 

using definition

Or  

Q 3: Compute

     We have  

.

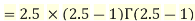
Q 4: Express in terms of gamma function

Given   I =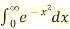 

Let

Then

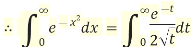
Q 5: Prove that

We know that

Putting

….(1)

Again putting

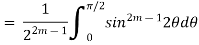
Let

When

Or    ….(2)

From (1) and (2) we get

Q 6: Solve the following

Solution:

= 

=

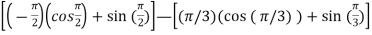
= (0+1)-

= 1+

=

Q 7: solve the integral

Solution:

Given,

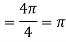
Q 8: Solve the following by using Leibniz Rule

Differentiate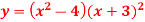 

Solution:

Using,

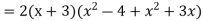
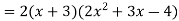
Q 9: Solve the following

Solution:

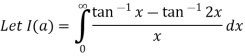
And Hence,

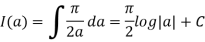
To get rid of the constant C , notice that I(1)=0, so

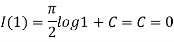
Therefore,