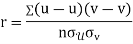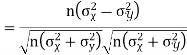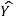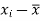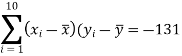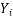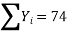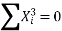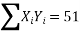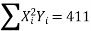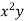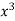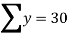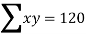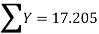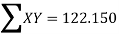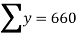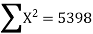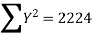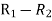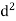UNIT 5
Statistics
Q1) Fit a least square line for the following data. Also find the trend values and show that ∑(Y– )=0 ∑(Y–
)=0 ∑(Y–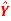 )=0.
)=0.
X | 1 | 2 | 3 | 4 | 5 |
Y | 2 | 5 | 3 | 8 | 7 |
A1):
X | Y | XY | X2 |
| Y– |
1 | 2 | 2 | 1 | 2.4 | -0.4 |
2 | 5 | 10 | 4 | 3.7 | +1.3 |
3 | 3 | 9 | 9 | 5.0 | -2 |
4 | 8 | 32 | 16 | 6.3 | 1.7 |
5 | 7 | 35 | 25 | 7.6 | -0.6 |
∑X=15 | ∑Y=25 | ∑XY=88 | ∑X 2=55 | Trend Values | ∑(Y-
|
The equation of least square line Y=a +bX
Normal equation for ‘a’ ∑Y=na+b 25=5a+15b —- (1)
Normal equation for ‘b’ ∑XY = a∑X+b∑X2 88=15a+55b —-(2)
Eliminate a a from equation (1) and (2), multiply equation (2) by 3 and subtract from equation (2).
Eliminate a from equation (1) and (2), multiply equation (2) by (3) and subtract from equation (2). Thus we get the values of a and b
Here a=1.1 and b=1.3 , the equation of least square line becomes
Y=1.1+1.3X
Q2) Using least square method to fit a straight line of the following data
X | 8 | 2 | 11 | 6 | 5 | 4 | 12 | 9 | 6 | 1 |
y | 3 | 10 | 3 | 6 | 8 | 12 | 1 | 4 | 9 | 14 |
Solution:
First we calculate  for the given data
for the given data

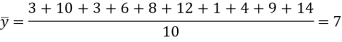
Now we calculate 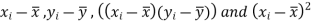
i |
|
|
|
|
|
|
1 | 8 | 3 | 1.6 | -4 | -6.4 | 2.56 |
2 | 2 | 10 | -4.4 | 3 | -13.2 | 19.36 |
3 | 11 | 3 | 4.6 | -4 | -18.4 | 21.16 |
4 | 6 | 6 | -0.4 | -1 | 0.4 | 0.16 |
5 | 5 | 8 | -1.4 | 1 | -1.4 | 1.96 |
6 | 4 | 12 | -2.4 | 5 | -12 | 5.76 |
7 | 12 | 1 | 5.6 | -6 | -33.6 | 31.36 |
8 | 9 | 4 | 2.6 | -3 | -7.8 | 6.76 |
9 | 6 | 9 | -0.4 | 2 | -0.8 | 0.16 |
10 | 1 | 14 | -5.4 | 7 | -37.8 | 29.16 |
|
|
|
|
|
|
|
Calculate the slope
m =  = -131/118.4
= -131/118.4 
calculate the y-intercept
use the formula to calculate the y-intercept
b = 
= 7-(-1.1*6.4)

The required line equation is
Y= -1.1x+14.0
Q3)
X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Y | 2 | 6 | 7 | 8 | 10 | 11 | 11 | 10 | 9 |
Solution:
X |
|
|
|
|
|
|
|
1 | -4 | 2 | 16 | -64 | 256 | -8 | 32 |
2 | -3 | 6 | 9 | -27 | 81 | -8 | 54 |
3 | -2 | 7 | 4 | -8 | 16 | -14 | 28 |
4 | -1 | 8 | 1 | -1 | 1 | -8 | 8 |
5 | 0 | 10 | 0 | 0 | 0 | 0 | 0 |
6 | 1 | 11 | 1 | 1 | 1 | 11 | 11 |
7 | 2 | 11 | 4 | 8 | 16 | 22 | 44 |
8 | 3 | 10 | 9 | 27 | 81 | 30 | 90 |
9 | 4 | 9 | 16 | 64 | 256 | 36 | 144 |
N=0 |
|
|
|
|
|
|
|
∑Y i =Na+b∑X i +c∑
∑X i Y i =a∑X i +b∑ +c∑
+c∑
∑ Y i =a∑
Y i =a∑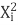 +b∑
+b∑ +c∑
+c∑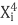
The required parabola is of the form y= ax2+bx+c
∴74=9a+b(0)+60c∴9a+60c=74…(i)
51=a(0)+60b+0c ∴60b=51 ∴b=5160 =0.85411=60a+0b+708 c∴60a+708c=411…(ii)
Solving (i) and (ii) simultaneously, we get
a=10.004 , c=-0.267
The Equation of parabola is therefore,
y=10.004+0.85X−0.267X 2
=10.004+0.85(x−5)−0.267(x−5) 2
=10.004+0.85x−4.25−0.267(x 2 −10x+25)
=10.004+0.85x−4.25−0.267x 2 +2.67x−6.675
∴ y = −0.921+3.52x−0.267x 2
Q4) Find the least square approximation of degree two to the data
X | 0 | 1 | 2 | 3 | 4 |
y | -4 | -1 | 4 | 11 | 20 |
Solution:
x | y | xy |
|
|
|
|
0 | -4 | 0 | 0 | 0 | 0 | 0 |
1 | -1 | -1 | 1 | -1 | 1 | 1 |
2 | 4 | 8 | 4 | 16 | 8 | 16 |
3 | 11 | 33 | 9 | 99 | 27 | 81 |
4 | 20 | 80 | 16 | 320 | 64 | 256 |
|
|
|
|
|
|
|
the normal equations are:



Here,
n = 5, 


by substituting all the above values in normal equations we get,
30 = 5a+10b+30c
120=10a+30b+100c
434=30a+100b+354c
By solving the above equations we get
a = -4, b=2,c=1.
Therefore the required polynomial is
Y= -4x+2x+x2 and errors =0
Q5) Determine the constants a and b by the method of least square such that 
X | 2 | 4 | 6 | 8 | 10 |
y | 4.077 | 11.084 | 30.128 | 81.897 | 222.62
|
Solution:
The given relation is 
Taking logarithms on both sides we get,
log y = log a+ bx…..(1)
let,
log y = Y
x = X
log a = A
b = B
now we have,
 ….(2)
….(2)
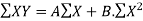 ….(3)
….(3)
Now we need to find 
X=x | Y =ln(y) |
| xy |
2 | 1.405 | 4 | 2.810 |
4 | 2.405 | 16 | 9.620 |
6 | 3.405 | 36 | 20.430 |
8 | 4.405 | 44 | 35.240 |
10 | 5.405 | 100 | 54.050 |
|
|
|
|
The normal equations to fit the straight line is
Y = logey
Y= ln(y)
17.025 = 5A +30B…..(4) 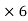
122.150 = 30A+220B….(5)
By solving 4 and 5 we get
30A +180B = 102.15…(4)
30A+220B = 122.150…(5)
We get a = 0.405 ,b = 0.5
A =log a 
a = 1.499
since we have X=x and Y=y
log y=Y,
And we know y= aebx
Y = (1.499)e0.5x is the required exponential curve.
Q6) Fit the curve of the form y= aebx for the following data
X | 0 | 2 | 4 |
Y | 8.12 | 10 | 31.82 |
Solution:
The given relation is 
Taking logarithms on both sides we get,
log y = log a+ bx logee…..(1)
the required normal equations are,
 ….(2)
….(2)
 ….(3)
….(3)
We have n=3
x | Y | Y= logey | xy | X2 |
0 | 8.12 | 2.0943 | 0 | 0 |
2 | 10 | 2.3026 | 4.6052 | 4 |
4 | 31.82 | 3.4601 | 13.8404 | 16 |
|
|
|
|
|
The normal equations become
3A +6b = 7.8750
6A + 20 b = 18.4456
By solving the above two equations we get
A = 1.361 and b = 0.3415
Since A =logea 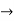 a = e1.361 = 6.9317
a = e1.361 = 6.9317
The curve of the fit is 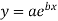
Thus,the required equation is,

Q 7) Ten students got the following percentage of marks in Economics and Statistics
Calculate the  of correlation.
of correlation.
Roll No. |
|
|
|
|
|
|
|
|
|
|
Marks in Economics |
|
|
|
|
|
|
|
|
|
|
Marks in |
|
|
|
|
|
|
|
|
|
|
Solution:. Let the marks of two subjects be denoted by  and
and  respectively.
respectively.
Then the mean for  marks
marks  and the mean ofy marks
and the mean ofy marks 
 and
and are deviations ofx’s and
are deviations ofx’s and  ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | y | X=x-65 | Y=y-66 | X2 | Y2 | XY |
78 36 98 25 75 82 90 62 65 39 | 84 51 91 60 68 62 86 58 53 47 | 13 -29 33 -40 10 17 25 -3 0 -26 | 18 -15 25 -6 2 -4 20 -8 -13 -19 | 169 841 1089 1600 100 289 625 9 0 676 | 324 225 625 36 4 16 400 64 169 361 | 234 435 825 240 20 -68 500 24 0 494
|
|
|
|
|
|
|
|

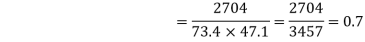
Q8: Find the correlation  betweenx and
betweenx and  , when the lines ofregression are:
, when the lines ofregression are:  and
and 
Solution. Let the line of regression ofx on  be
be 
Then, the line ofregressionofy on  is
is 

and
 which is not possible. So our choice of regression line is incorrect.
which is not possible. So our choice of regression line is incorrect.
The regression line ofx on  is
is 
And, the regression line ofy on  is
is 
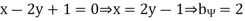
And 

Hence the correlation coefficient between 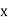 and
and  is
is 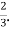
Q9) The following regression equations were obtainedfrom a correlation table:

Find the value of  the correlation coefficient,
the correlation coefficient,
(b) the mean 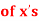 and
and
(c) the mean of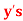
Solution.

(a) From (1), 
(b) From (2), 
From (3) and (4)


Coefficient of correlation 

(b) (1) and (2) pass through the point  .
.
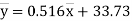 (5)
(5)
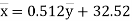 (6)
(6)
On solving (5) and (6), we get

Q10) Compute Spearman’s rank correlation coefficient r for the following data:
Person | A | B | C | D | E | F | G | H | I | J |
Rank Statistics | 9 | 10 | 6 | 5 | 7 | 2 | 4 | 8 | 1 | 3 |
Rank in income | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Solution:
Person | Rank Statistics | Rank in income | d= |
|
A | 9 | 1 | 8 | 64 |
B | 10 | 2 | 8 | 64 |
C | 6 | 3 | 3 | 9 |
D | 5 | 4 | 1 | 1 |
E | 7 | 5 | 2 | 4 |
F | 2 | 6 | -4 | 16 |
G | 4 | 7 | -3 | 9 |
H | 8 | 8 | 0 | 0 |
I | 1 | 9 | -8 | 64 |
J | 3 | 10 | -7 | 49 |


Q11) If X and Y are uncorrelated random variables,  the
the  of correlation between
of correlation between 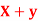 and
and 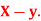
Solution.
Let  and
and 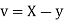
Then 
Now 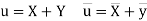
Similarly 
Now 




Also 
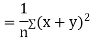

 (As
(As  and
and  are not correlated, we have
are not correlated, we have 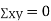 )
)
Similarly