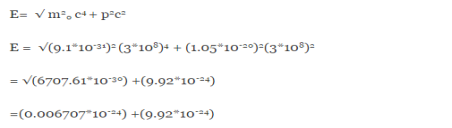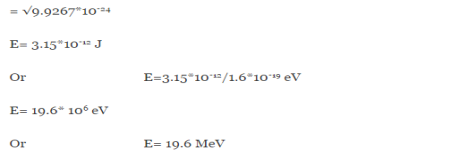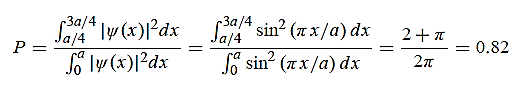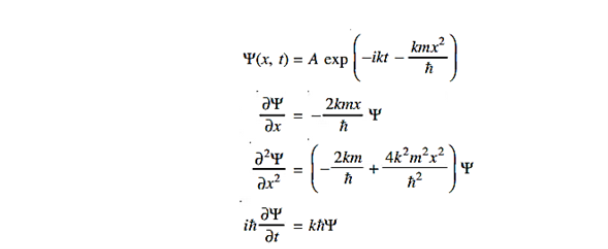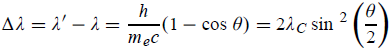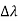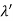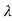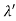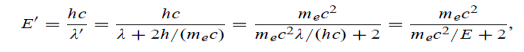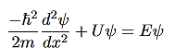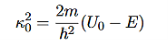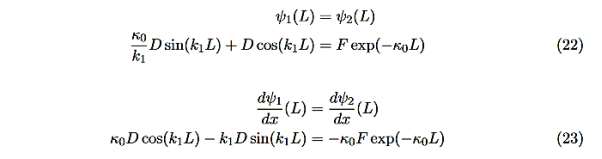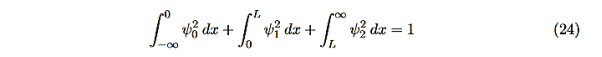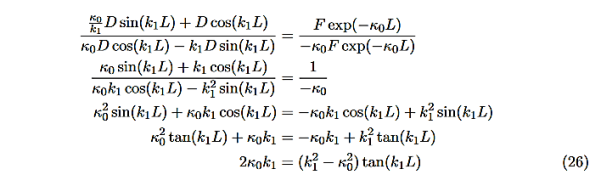behaves as a group of waves (matter waves) whose wavelength λ and wave vector
behaves as a group of waves (matter waves) whose wavelength λ and wave vector  are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed. λ =
are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed. λ =  =
=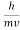 …….(1)
…….(1)  =
=  …….(2) Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation. λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment. However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c. Therefore
…….(2) Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation. λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment. However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c. Therefore =
=  = λ Q2) What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?A 2) (a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s)p = 4.92 × 10–24 kg m/sde Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/sλ= 0.135 nm(b)For the ball:Mass m’ = 0.150 kg, Speed v’= 30.0 m/s.Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s)p’= 4.50 kg m/sde Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 mThe de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement. Q3) What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volts?A 3)Accelerating potential V = 100 V. The de Broglie wavelength λ is λ= h /p = 1 227/
= λ Q2) What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?A 2) (a)For the electron: Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s. Then, momentum p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s)p = 4.92 × 10–24 kg m/sde Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/sλ= 0.135 nm(b)For the ball:Mass m’ = 0.150 kg, Speed v’= 30.0 m/s.Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s)p’= 4.50 kg m/sde Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 mThe de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement. Q3) What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volts?A 3)Accelerating potential V = 100 V. The de Broglie wavelength λ is λ= h /p = 1 227/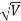 nmλ.1 227/
nmλ.1 227/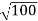 nm = 0.123 nmThe de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths. Q4) What is Heisenberg’s Uncertainty Principle?A 4)According to classical physics, given the initial conditions and the forces acting on a system, the future behaviour (unique path) of this physical system can be determined exactly. That is, if the initial coordinates
nm = 0.123 nmThe de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths. Q4) What is Heisenberg’s Uncertainty Principle?A 4)According to classical physics, given the initial conditions and the forces acting on a system, the future behaviour (unique path) of this physical system can be determined exactly. That is, if the initial coordinates , velocity
, velocity 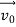 , and all the forces acting on the particle are known, the position
, and all the forces acting on the particle are known, the position 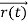 , and velocity
, and velocity  are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.Does this hold for the microphysical world? Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle.In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.Does this hold for the microphysical world? Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle.In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
|
v = 20m/s,m = 0.5kg,h = 6.626 × 10-34 m2 kg / sΔp =p×1×10−6As we know that,
P = m×v = 0.5×20 = 10kgm/s
Δp = 10×1×10−6Δp = 10-5Heisenberg Uncertainty principle formula is given as,∆x∆p
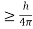 ∆x
∆x  ∆x
∆x 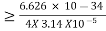 ∆x =0.527 x 10-29 mQ6) Prove non-existence of electrons in the nucleus?A 6)One of the applications is to prove that electron cannot exist inside the nucleus. But to prove it, let us assume that electrons exist in the nucleus. As the radius of the nucleus in approximately 10-14m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given byAccording to uncertainty principle∆x ∆p =h/2πThus ∆p=h/2π∆xOr ∆p=6.62 x10-34/2 x 3.14 x 10-14Or ∆p=1.05 x 10-20 kg m/ secIf this is p the uncertainty in the momentum of electron, then the momentum of electron should be at least of this order that is p=1.05*10-20 kg m/sec.An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formulaE =
∆x =0.527 x 10-29 mQ6) Prove non-existence of electrons in the nucleus?A 6)One of the applications is to prove that electron cannot exist inside the nucleus. But to prove it, let us assume that electrons exist in the nucleus. As the radius of the nucleus in approximately 10-14m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given byAccording to uncertainty principle∆x ∆p =h/2πThus ∆p=h/2π∆xOr ∆p=6.62 x10-34/2 x 3.14 x 10-14Or ∆p=1.05 x 10-20 kg m/ secIf this is p the uncertainty in the momentum of electron, then the momentum of electron should be at least of this order that is p=1.05*10-20 kg m/sec.An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formulaE = 
|
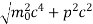
|
 =
= 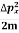 =
= Where m is the mass of the particle.Energy even at O K is given by the above equation. This minimum energy is called the zero-point energy.This implies that even at zero kelvin, the particle is never at rest. If it is so, then ∆pX = 0, which is not possible. [It gives ∆x = ∞]3. Existence of proton, neutron and alpha particles within the nucleus.We know that the rest mass of the protons and neutron is of the order of 1.67x 10-27 kg. Hence, the value of momentum 5.27 x 10-21 kg.m/sec from calculation and also the value of v come out to be 3x 105m/sec. The corresponding value of kinetic energy of a neutron or a proton isE =
Where m is the mass of the particle.Energy even at O K is given by the above equation. This minimum energy is called the zero-point energy.This implies that even at zero kelvin, the particle is never at rest. If it is so, then ∆pX = 0, which is not possible. [It gives ∆x = ∞]3. Existence of proton, neutron and alpha particles within the nucleus.We know that the rest mass of the protons and neutron is of the order of 1.67x 10-27 kg. Hence, the value of momentum 5.27 x 10-21 kg.m/sec from calculation and also the value of v come out to be 3x 105m/sec. The corresponding value of kinetic energy of a neutron or a proton isE = 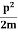 =
= 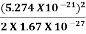 =8.33 x 10-15J =
=8.33 x 10-15J =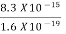 eV
eV  52.05 keVSince the rest mass of the a-particle is nearly four times the proton mass, therefore the alpha particle should have a minimum kinetic energy of one fourth of 52.05 keV, or about 13 keV. Since the energy carried by the protons or neutrons emitted by the nuclei are greater than 52 keV and for a-particle more than 13 keV, these particles can exist in the nuclei.4. Size of Elementary cell in Phase spaceWe have studied in our previous class that state of a microsystem is defined by six variables – three are due to position and three due to momentum. Hence, a system of N particles needs 6 N variables If ∆ x and ∆px be the uncertainly in position and in momentum measurements, then ∆ x ∆ px =
52.05 keVSince the rest mass of the a-particle is nearly four times the proton mass, therefore the alpha particle should have a minimum kinetic energy of one fourth of 52.05 keV, or about 13 keV. Since the energy carried by the protons or neutrons emitted by the nuclei are greater than 52 keV and for a-particle more than 13 keV, these particles can exist in the nuclei.4. Size of Elementary cell in Phase spaceWe have studied in our previous class that state of a microsystem is defined by six variables – three are due to position and three due to momentum. Hence, a system of N particles needs 6 N variables If ∆ x and ∆px be the uncertainly in position and in momentum measurements, then ∆ x ∆ px =  ; Similarly ∆ y ∆ py =
; Similarly ∆ y ∆ py =  , And ∆ z ∆ pz =
, And ∆ z ∆ pz =  , Multiplying these three equations, we get ∆ x ∆ y ∆ z ∆ px ∆ py ∆ pz = (
, Multiplying these three equations, we get ∆ x ∆ y ∆ z ∆ px ∆ py ∆ pz = (  )3 in the units (J3 S3).The above product is called the volume of elementary cell in phase space.So, volume of an elementary cell in phase space
)3 in the units (J3 S3).The above product is called the volume of elementary cell in phase space.So, volume of an elementary cell in phase space  10-101 units, (for quantum statistics) being
10-101 units, (for quantum statistics) being 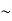
 .5. Accurate limit of frequency of radiation emitted by an atomConsider the radiation emitted from an excited atom. The energy of this atom will decrease when it emits one or more photons of characteristic frequency. The average period between excitation of the atom and the release of energy is about 10-8 seconds.Thus, uncertainly in energy is ∆ E
.5. Accurate limit of frequency of radiation emitted by an atomConsider the radiation emitted from an excited atom. The energy of this atom will decrease when it emits one or more photons of characteristic frequency. The average period between excitation of the atom and the release of energy is about 10-8 seconds.Thus, uncertainly in energy is ∆ E 
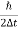 Or ∆ E
Or ∆ E 
 J Or ∆ E
J Or ∆ E  5.3 x 10-27 J Frequency of light is uncertain by ∆ ν =
5.3 x 10-27 J Frequency of light is uncertain by ∆ ν =  =
=  Hz
Hz  0.8 x 107 HzAs a result, the radiation from an excited atom does not have the noted precise frequency new ν - ∆ ν and ν + ∆ ν. Q8) Derive the Schrodinger wave equation?A 8)Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x. So We have E= K+V =
0.8 x 107 HzAs a result, the radiation from an excited atom does not have the noted precise frequency new ν - ∆ ν and ν + ∆ ν. Q8) Derive the Schrodinger wave equation?A 8)Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x. So We have E= K+V = mv2+V(x) =
mv2+V(x) = +V(x) ……….. (1) By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk. Using this equation (1) for the energy will becomeℏω =
+V(x) ……….. (1) By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk. Using this equation (1) for the energy will becomeℏω = 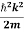 + V(x) ……….. (2) A wave with frequency ω and wave number k can be written as usual asψ(x, t) =Aei(kx−ωt) ……….. (3) the above equation is for one dimensional and for three dimensional we can write it as ψ(r, t) =Aei(k·r−ωt) ……….. (4) But here we will stick to one dimension only.
+ V(x) ……….. (2) A wave with frequency ω and wave number k can be written as usual asψ(x, t) =Aei(kx−ωt) ……….. (3) the above equation is for one dimensional and for three dimensional we can write it as ψ(r, t) =Aei(k·r−ωt) ……….. (4) But here we will stick to one dimension only. =−iωψ ⇒ ωψ=
=−iωψ ⇒ ωψ=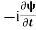 ……….. (5)
……….. (5)  =−k2ψ ⇒ k2ψ = -
=−k2ψ ⇒ k2ψ = -  ……….. (6) If we multiply the energy equation in Eq. (2) by ψ, and using (5) and (6) , we obtain ℏ(ωψ) =
……….. (6) If we multiply the energy equation in Eq. (2) by ψ, and using (5) and (6) , we obtain ℏ(ωψ) =  ψ+ V(x) ψ ⇒
ψ+ V(x) ψ ⇒ 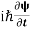 = -
= - 
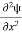 + V(x) ψ ……….. (7) This is the time-dependent Schrodinger equation. If we put the x and t in above equation then equation (7) takes the form as given below
+ V(x) ψ ……….. (7) This is the time-dependent Schrodinger equation. If we put the x and t in above equation then equation (7) takes the form as given below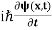 = -
= - 
 + V(x) ψ(x,t) ……….. (8) In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the
+ V(x) ψ(x,t) ……….. (8) In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the  term becomes ∇2ψ. The term |ψ(x)|2 gives the probability of finding the particle at position x. Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7) But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
term becomes ∇2ψ. The term |ψ(x)|2 gives the probability of finding the particle at position x. Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7) But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields  = -
= - 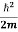
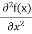 + V(x) f(x) ……….. (9) We already know that E=
+ V(x) f(x) ……….. (9) We already know that E= . However ψ(x, t) is general convention to also use the letter ψ to denote the spatial part. So we will now replace f(x) with ψ(x) Eψ = -
. However ψ(x, t) is general convention to also use the letter ψ to denote the spatial part. So we will now replace f(x) with ψ(x) Eψ = - 
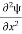 + V(x) ψ ……….. (10) This is called the time-independent Schrodinger equation.The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics. Q9) The mass of an electron is 9.1×10–31 kg. Its uncertainty in velocity is 5.7×105 m/sec. Calculate uncertainty in its position?A 9)Given m= 9×10–31ΔV= 5.7×105 m/sec Δx=?h= 6.6×10–34 Joule-Sec.Δx.Δv ≥h/4πmΔx≥h/4πmΔv≥6.6×10–34/9×3.14×9.1×10–31×5.7×105≥ 0.010×10–8≥ 1×10–10m Q10) The mass of a ball is 0.15 kg & its uncertainty in position to 10–10m. What is the value of uncertainty in its velocity?A 10)Given m=0.15 kg. h=6.6×10-34 Joule-Sec.Δx = 10 –10 mΔv=?Δx.Δv ≥h/4πmΔv≥h/4πmΔx≥6.6×10-34/4×3.14×0.15×10–10≥ 3.50×10–24m Q11) The mass of a bullet is 10gm & uncertainty in its velocity is 5.25×10–26 cm/sec. Calculate the uncertainty in its position?A 11)m=10 gm. h=6.6×10–27 erg-secΔv= 5.25×10–26 cmΔx=?Δx.Δv ≥h/4πmΔx≥h/4πmΔv≥6.6×10-34/4×3.14×10×5.25×10–26≥ 0.10×10–2m≥ 1×10–3 cmQ12) List the conditions wave function should satisfy?A 12)The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x. The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as ψ(x, y, z, t) = a + ib and its complex conjugate as ψ*(x, y, z, t) = a – ib. The product of wave function and its complex conjugate is ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2 a2 + b2 is a real quantity. However, this can represent the probability density of locating the particle at a place in a given instant of time. The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number. We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one. For the probability interpretation to make sense, the wave function must satisfy certain conditions.
+ V(x) ψ ……….. (10) This is called the time-independent Schrodinger equation.The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics. Q9) The mass of an electron is 9.1×10–31 kg. Its uncertainty in velocity is 5.7×105 m/sec. Calculate uncertainty in its position?A 9)Given m= 9×10–31ΔV= 5.7×105 m/sec Δx=?h= 6.6×10–34 Joule-Sec.Δx.Δv ≥h/4πmΔx≥h/4πmΔv≥6.6×10–34/9×3.14×9.1×10–31×5.7×105≥ 0.010×10–8≥ 1×10–10m Q10) The mass of a ball is 0.15 kg & its uncertainty in position to 10–10m. What is the value of uncertainty in its velocity?A 10)Given m=0.15 kg. h=6.6×10-34 Joule-Sec.Δx = 10 –10 mΔv=?Δx.Δv ≥h/4πmΔv≥h/4πmΔx≥6.6×10-34/4×3.14×0.15×10–10≥ 3.50×10–24m Q11) The mass of a bullet is 10gm & uncertainty in its velocity is 5.25×10–26 cm/sec. Calculate the uncertainty in its position?A 11)m=10 gm. h=6.6×10–27 erg-secΔv= 5.25×10–26 cmΔx=?Δx.Δv ≥h/4πmΔx≥h/4πmΔv≥6.6×10-34/4×3.14×10×5.25×10–26≥ 0.10×10–2m≥ 1×10–3 cmQ12) List the conditions wave function should satisfy?A 12)The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x. The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as ψ(x, y, z, t) = a + ib and its complex conjugate as ψ*(x, y, z, t) = a – ib. The product of wave function and its complex conjugate is ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2 a2 + b2 is a real quantity. However, this can represent the probability density of locating the particle at a place in a given instant of time. The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number. We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one. For the probability interpretation to make sense, the wave function must satisfy certain conditions. 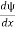 must also be continuous everywhere except where V(x) is infinite.
must also be continuous everywhere except where V(x) is infinite. 0 as x
0 as x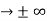 .
.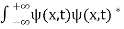 dx =1 Only wave function with all these properties can yield physically meaningful result. Q13) What is Physical significance of wave function?A 13)
dx =1 Only wave function with all these properties can yield physically meaningful result. Q13) What is Physical significance of wave function?A 13)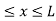 ………. (1)V=
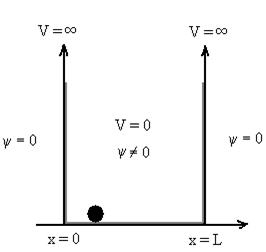
………. (1)V=  for x <0, x>L ………. (2)
for x <0, x>L ………. (2)
|
 ψ +
ψ + E ψ =0 …………….(2) Substituting
E ψ =0 …………….(2) Substituting 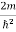 E = k2 …………….(3) writing the SWE for 1-D we get
E = k2 …………….(3) writing the SWE for 1-D we get  + k2 ψ =0 …………….(4) The general equation of above equation may be expressed asψ = Asin (kx + ϕ) …………….(5)Where A and ϕ are constants to be determined by boundary conditionsCondition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A
+ k2 ψ =0 …………….(4) The general equation of above equation may be expressed asψ = Asin (kx + ϕ) …………….(5)Where A and ϕ are constants to be determined by boundary conditionsCondition I: We have ψ = 0 at x = 0, therefore from equation 0 = A sinϕ As A 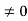 then sinϕ =0 or ϕ=0 …………….(6)Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5)0 = Asin kL As A
then sinϕ =0 or ϕ=0 …………….(6)Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5)0 = Asin kL As A  then sinkL =0 or kL=nπk =
then sinkL =0 or kL=nπk =  …………….(7)where n= 1,2,3,4………Substituting the value of k from (7) to (3)
…………….(7)where n= 1,2,3,4………Substituting the value of k from (7) to (3) 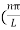 )2 =
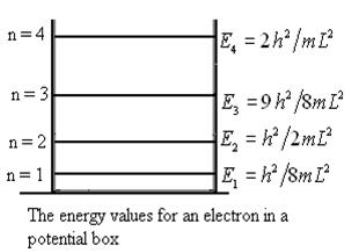
)2 =  E This gives energy of level En =
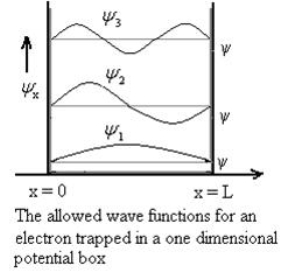
E This gives energy of level En =  n=1,2,3,4…so on …………….(8)
n=1,2,3,4…so on …………….(8) From equation En is the energy value (Eigen Value) of the particle in a well. It is clear that the energy values of the particle in well are discrete not continuous.
|
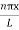 …………….(9)The probability density |ψ(x,t)|2 = ψ ψ*|ψ(x,t)|2 = A2sin2
…………….(9)The probability density |ψ(x,t)|2 = ψ ψ*|ψ(x,t)|2 = A2sin2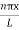 …………….(10)The probability density is zero at x = 0 and x = L. since the particle is always within the well
…………….(10)The probability density is zero at x = 0 and x = L. since the particle is always within the well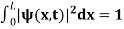 …………….(11)
…………….(11)

 =1A =
=1A =  Substituting A in equation (9) we getψ = ψn =
Substituting A in equation (9) we getψ = ψn =  sin
sin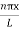 n=1,2,3,4….. …………….(12)The above equation (12) is normalized wave function or Eigen function belonging to energy value En
n=1,2,3,4….. …………….(12)The above equation (12) is normalized wave function or Eigen function belonging to energy value En
|
|
 1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q16) Consider a one-dimensional particle which is confined within the region 0
1031, the quantum nature of this radiation is unimportant. As a result, this radiation can be treated fairly accurately by the classical theory of electromagnetism.Q16) Consider a one-dimensional particle which is confined within the region 0  x
x a and whose wave function is (x, t) =sin(πx/a) exp-iωt.(a) Find the potential V(x).(b) Calculate the probability of finding the particle in the interval a/4
a and whose wave function is (x, t) =sin(πx/a) exp-iωt.(a) Find the potential V(x).(b) Calculate the probability of finding the particle in the interval a/4  x
x  3a/4.A 16)Since the first time derivative and the second x derivative of (x, t), are given by
3a/4.A 16)Since the first time derivative and the second x derivative of (x, t), are given by
Hence V(x,t) is time independent and given by
(b) The probability of finding the particle in the interval a/4
|
|
|
 where A and k are constants. Find the explicit form of the potential V (x). A 19)
where A and k are constants. Find the explicit form of the potential V (x). A 19)
Substituting these values in the time dependendent Schrödinger equation, we have
|
|
 , called the wavelength shift, and that
, called the wavelength shift, and that 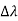 depends not on the intensity of the incident radiation, but only on the scattering angle. Compton succeeded in explaining his experimental results only after treating the incident radiation as a stream of particles—photons—colliding elastically with individual electrons. Here we will discuss elastic scattering of a photon from a free electron as shown in figure. Consider that the incident photon, of energy E =hν and momentum p = hν /c, collides with an electron that is initially at rest. If the photon scatters with a momentum
depends not on the intensity of the incident radiation, but only on the scattering angle. Compton succeeded in explaining his experimental results only after treating the incident radiation as a stream of particles—photons—colliding elastically with individual electrons. Here we will discuss elastic scattering of a photon from a free electron as shown in figure. Consider that the incident photon, of energy E =hν and momentum p = hν /c, collides with an electron that is initially at rest. If the photon scatters with a momentum at an angle θ while the electron recoils with a momentum
at an angle θ while the electron recoils with a momentum  the conservation of linear momentum yields
the conservation of linear momentum yields =
= 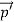 +
+  …………(1)Which leads
…………(1)Which leads
Energy Conservation The energies of the electron before and after the collision are given, respectively, by E0 =mec2 ………..(3)
Since the energies of the incident and scattered photons are given by E = hν and E0 = hν’, respectively, conservation of energy dictates that E + E0 = E’ + Ee ………..(4)
Which leads to
Squaring both sides of (5) and simplifying, we get
Hence wavelength shift is given by
Where λC = h/mec = 2.426 x 10-12 m is called the Compton wavelength of the electron.
|
(a) In the case where the photons backscatter i.e. θ = π The wavelength shift becomes
(b) Since the energy of the scattered photons E’ is related to the wavelength
Where E = hc/
(c) If E = 150 MeV, the kinetic energy of the recoiling electrons can be obtained from conservation of energy Ke = E – E’
|
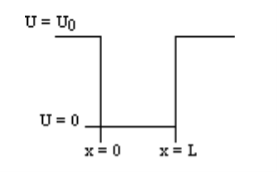
 x
x L (2)U=U0 L < x. (3)We want to solve Schroedinger’s Equation for this potential to get the wave functions and allowed energies for E < U0. We will refer to the three regions as regions 0, 1, and 2 with associated wave functions ψ0,ψ1,ψ2.
L (2)U=U0 L < x. (3)We want to solve Schroedinger’s Equation for this potential to get the wave functions and allowed energies for E < U0. We will refer to the three regions as regions 0, 1, and 2 with associated wave functions ψ0,ψ1,ψ2.
|
that can be rearranged to give
It is convenient to define two new variables (both positive), one for regions 0 and 2, and one for region 1—they are wavenumbers:
and Schrödinger’s equation becomes
In regions 0 and 2 the general solution is a linear combination of exponentials with the same form, but with different constants, namely
In region 1 we have the same general solution that we had for the infinite square well,
Equations (10) to (12) have 7 unknowns—A,B,C,D,F,G and the energy E that is im-plicitly contained in the variables κ0,k1. Therefore we need to get 7 equations to be ableto solve for the unknowns. We will first use the requirement that the wavefunction remain finite everywhere. Consider ψ2 as x→∞. For this to remain finite we must require G= 0. Similarly, as x→−∞, we require A= 0. Our solutions become
The next step is to require that the wavefunction and its first derivative be continuous everywhere, and in our case we look at the boundaries, x= 0 and x=L.
Hence ψ0=D exp(+κ0x).Take derivatives of the wave functions,
There remain 3 unknowns, D,F, and E. Finding them is a bit messier! Consider the boundary conditions at x=L,
We are not going much farther, but if we divided Equation (22) by Equation (23), we can see that the constants D and F cancel leaving us with one rather difficult equation to solve for energy E (remember this is implicitly included in the values of k1and κ0.) There is one remaining condition, normalization, that for this problem is
Even without solving the entire problem we can make some conclusions about the wave-function and the allowed energy levels. Recall that for an infinite square well potential of width L the allowed energies are quantized and
Here is Equation(22)/Equation(23)
Now put in the values ofκ0andk1from Equations (6) and (7) and do some algebra to get
This equation is a single equation in a single unknown, E < U0. Once we have the details of our particle (its mass) and the potential energy (depth U0 and width L), we can solve it. There is no analytic solution, only a numerical one. From equation (25) With n being any positive integer. Outside the well the wavefunction is 0. We are certain that the particle is somewhere inside the box, so ∆x ∞ =L. With the finite well, the wavefunction is not zero outside the well,
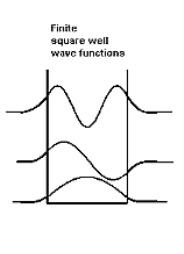
Figure 9: Wave function in Finite well So ∆x finite> L, hence from the uncertainty principle, ∆pfinite x<∆p∞x. This suggests that the average value of momentum is less for the finite well, and therefore that the kinetic energy inside the well is less for the finite well than for the infinite well. Indeed this is borne out with detailed analysis. In addition, the number of allowed energy levels is finite, and there is a possibility that a well may be sufficiently narrow or sufficiently shallow that no energy levels are allowed. Also note that the non-zero wave functions in regions 0 and 2 mean that there is a non-zero probability of finding the particle in a region that is classically forbidden, a region where the total energy is less than the potential energy so that the kinetic energy is negative.
|