EM
UNIT-1ENGINEERING MECHANICS Q1) A 90 N force is applied to the control rod AB. Determine moment of this Force about point B.A 1) Solution:- As we don’t know perpendicular distance betn force & point ‘ B ’, Let us resolve the force into two components.
X – Component of force Fx = 90 Cos 25 = 81.567 NY – Component of force Fy = 90 Sin 25 = 38.036Now taking moments about point B.MB = [Fx x (3 Sin 65)] - [Fy x (3 Cos 65)]MB = (81.65 x 2.72) – (38.036 x 1.27) = 221.843 – 48.31MB = 173.53 N.m Q2) Determine the FR when three forces such as 80 N, 100 N, and 30 N are acting on an object simultaneously and 30 N force is opposite to the other two forces.S2)Given:F1 = 80 NF2 = 100 NF3 = -30 NF3 is a negative value because it is acting opposite to the other two forceThe formula for resultant force isFR = F1+F2+F3FR = 80 + 100 – 30FR = 150 N Q 3) Find support reactions for the loading as shown below:
= 221.843 – 48.31MB = 173.53 N.m Q2) Determine the FR when three forces such as 80 N, 100 N, and 30 N are acting on an object simultaneously and 30 N force is opposite to the other two forces.S2)Given:F1 = 80 NF2 = 100 NF3 = -30 NF3 is a negative value because it is acting opposite to the other two forceThe formula for resultant force isFR = F1+F2+F3FR = 80 + 100 – 30FR = 150 N Q 3) Find support reactions for the loading as shown below:
A 3) Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0 Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN
Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0 Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN  Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN
Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN  Q 4) Find the reactions at support A & B.
Q 4) Find the reactions at support A & B.
A 4) Resolving forces vertically∑fy = 0RVA – 30 – 80 + RB = 0RVA + RB = 110 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0 Taking moments at A∑ MA = 0(30 × 0.6) + [80 × (4.07 + 0.6)]- (6 × RB) = 018 + 373.6 – 6RB = 06RB = 391.6RB= 65.267 kNPut above value in equation (1)RVA + RB = 110RVA + 65.267 = 110RVA = 110 – 65.267RVA = 44.733 kN Q 5) Explain the different types of beams?A 5) Beam – It is horizontal structural member on which different types of loads can be supported. It takes load from floor or roof & transfers to column.The beam may be sometimes constructed in the inclined position for architectural point of view.Types of Beam: -
Resolving forces vertically∑fy = 0RVA – 30 – 80 + RB = 0RVA + RB = 110 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0 Taking moments at A∑ MA = 0(30 × 0.6) + [80 × (4.07 + 0.6)]- (6 × RB) = 018 + 373.6 – 6RB = 06RB = 391.6RB= 65.267 kNPut above value in equation (1)RVA + RB = 110RVA + 65.267 = 110RVA = 110 – 65.267RVA = 44.733 kN Q 5) Explain the different types of beams?A 5) Beam – It is horizontal structural member on which different types of loads can be supported. It takes load from floor or roof & transfers to column.The beam may be sometimes constructed in the inclined position for architectural point of view.Types of Beam: -Simply supported beam – A beam which is just resting on the supports at the end without any connection is known as simply supported beam. It is generally used for vertical landing system.
2. Overhanging Beam – A beam which is supported at the intermediate point other than ends is called as overhanging beam. Here portion of beam is extended beyond the support
3. Cantilever Beam –A beam which is fixed at one end is called as cantilever beam
Here, there are three reactions components:Vertical reaction at A (RVA) Horizontal reaction at A (RHA) Fixing moment at A (MA) We can assume any direction for above components.4. Continuous Beam: A beam having more than two supports is called as continuous beam.
5. Compound Beam: When two or more beams are joined together by using internal hinge; or when one beam rests over another beam by using internal roller, then such beam is called as compound beam.
Q5) Two forces of 100 N & 150 N are acting simultaneously at a point. What is the resultant of these two forces, if the angle between them is 450?A5)
Given: P = 100 N Q = 150 N θ = 45o R =? α=? Solution:According to law of parallelogram of force,R = √ P2 + Q2 + 2PQ Cos θR = √ 1002 + 1502 + 2 x 100 x 150 x Cos 450R = 231.76 NR ≈ 232 N - - - Answer - - - magnitudetanα = Q Sin θ / P + Q Cos θ = 150 Sin 450 / 100 + 150 Cos 450 = 106.066 / 206.066 α = 27.290. . . . . Direction Q 6) The sum of two forces is 270 N & their resultant is 180 N. If Resultant is Perpendicular to P, find the two forces P & Q.A 6)Given:
P + Q = 270 NR = 180 N α = 900Solution : According to law of parallelogram,Tanα = Q Sin θ / P + Q Cos θTan 90 = Q Sin θ / P + Q Cos θ∞ = Q Sin θ / P + Q Cos θHere if P + Q Cos θ = 0, then only above term will become infinity.Thus, P + Q Cosθ= 0 P = - Q Cos θ-P = Q Cosθ . . . . (1)Now, R2 = P2 + Q2 + 2PQ Cos θ 1802 = P2 + Q2 + 2P (-P) . . . from equation (1) 1802 = P2 + Q2 + (-2P2) 1802 = P2 -2P2 + Q2 1802 = - P2 + Q2 1802 = Q2 - P2 1802 = (Q- P) (Q+ P) = (Q- P) x 270 Q- P = 1802 / 270Q- P = 120 . . . (ii)& we know thatQ + P = 270 . . . (iii)Solving (ii) & (iii) i.e. add eqn (ii) & (iii) Q – P = 120 + Q + P = 270 _______________ 2Q + 0 = 390 
 2Q = 390Q = 195 N &P = 75 N . . . Answer Q 7) Explain the newton’s laws?A 7) Principles of Statics1- Newton’s 1stLaw: -Everybody continues to be in its state of rest or in the state of uniform motion along straight line unless it is acted upon by external unbalanced force.2. Newton’s 2ndLaw:-When unbalanced force acts on particle, it will have an acceleration which is proportional to the magnitude of force. This acceleration will be in the direction of force along straight line.Rate of change of momentum of body is directly proportional to the force acting on it & it is in the direction of force.3. Newton’s 3rdLaw:-Forces of action & reaction between bodies in contact will have same magnitude, line of action but opposite direction. Q 8) What is mechanics explain with classifications?A 8) Mechanics:-The branch of physical science that deals with state of the rest of the motion is called as mechanics.Engineering Mechanics: -The branch of applied science, which deals with laws & Principals of Mechanics along with their applications to the real life engineering problem.Engineering Mechanics is essential for an engineer in Planning, designing & construction of various structures & machines.Classification of Engineering Mechanics: -
2Q = 390Q = 195 N &P = 75 N . . . Answer Q 7) Explain the newton’s laws?A 7) Principles of Statics1- Newton’s 1stLaw: -Everybody continues to be in its state of rest or in the state of uniform motion along straight line unless it is acted upon by external unbalanced force.2. Newton’s 2ndLaw:-When unbalanced force acts on particle, it will have an acceleration which is proportional to the magnitude of force. This acceleration will be in the direction of force along straight line.Rate of change of momentum of body is directly proportional to the force acting on it & it is in the direction of force.3. Newton’s 3rdLaw:-Forces of action & reaction between bodies in contact will have same magnitude, line of action but opposite direction. Q 8) What is mechanics explain with classifications?A 8) Mechanics:-The branch of physical science that deals with state of the rest of the motion is called as mechanics.Engineering Mechanics: -The branch of applied science, which deals with laws & Principals of Mechanics along with their applications to the real life engineering problem.Engineering Mechanics is essential for an engineer in Planning, designing & construction of various structures & machines.Classification of Engineering Mechanics: -  Engineering Mechanics
Engineering Mechanics



 Mechanics of Solids Mechanics of Fluids
Mechanics of Solids Mechanics of Fluids  Mechanics of Rigid Bodies Mechanics of Deformable Bodies
Mechanics of Rigid Bodies Mechanics of Deformable Bodies




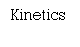
 Statics Dynamics In our syllabus, we are going to study the mechanics of Rigid Bodies i.e. Statics & Dynamics.Statics: -It is the branch of Engineering Mechanics which deals with the forces and their effects (acting) upon the bodies which are at rest.Dynamics: -It is the branch of engineering Mechanics which deals with forces & their effects (acting) upon the bodies which are in motion.Dynamics is again divided into two categories:1. Kinetics2. KinematicsKinetics:-It is the branch of Dynamics which deals with the bodies in motion by considering the forces which cause the motion.Kinematics:-It is the branch of Dynamics which deals with the bodies in motion without considering the force which is responsible for the motion.Mass (m ) :-The quantity of matter possessed by a body,S.I. unit: - gram (g) Kilogram (kg)1 kg = 1000 gWeight (W):-Force acting on the object due to gravity.It is the product of mass & gravitational Acceleration.W = m x gS.I. Unit: - Newton (N)Kilo Newton (KN)1 KN = 1000 N. Q 9) Find the support reactions for given beam. A 9)
Statics Dynamics In our syllabus, we are going to study the mechanics of Rigid Bodies i.e. Statics & Dynamics.Statics: -It is the branch of Engineering Mechanics which deals with the forces and their effects (acting) upon the bodies which are at rest.Dynamics: -It is the branch of engineering Mechanics which deals with forces & their effects (acting) upon the bodies which are in motion.Dynamics is again divided into two categories:1. Kinetics2. KinematicsKinetics:-It is the branch of Dynamics which deals with the bodies in motion by considering the forces which cause the motion.Kinematics:-It is the branch of Dynamics which deals with the bodies in motion without considering the force which is responsible for the motion.Mass (m ) :-The quantity of matter possessed by a body,S.I. unit: - gram (g) Kilogram (kg)1 kg = 1000 gWeight (W):-Force acting on the object due to gravity.It is the product of mass & gravitational Acceleration.W = m x gS.I. Unit: - Newton (N)Kilo Newton (KN)1 KN = 1000 N. Q 9) Find the support reactions for given beam. A 9)
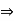 Resolving force horizontally∑fX = 0RHA = 0Resolving forces vertically∑fy = 0RVA + RB = 0 --------------- (1)Taking moments at A
Resolving force horizontally∑fX = 0RHA = 0Resolving forces vertically∑fy = 0RVA + RB = 0 --------------- (1)Taking moments at A 40 – 7RB = 0
40 – 7RB = 0 RB =
RB = 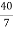 RB = 5.71 kN
RB = 5.71 kN  Put above value in equation (1)RVA + RB = 0RVA + 5.71 = 0 RVA = - 5.71 kN RVA = 5.71 kN
Put above value in equation (1)RVA + RB = 0RVA + 5.71 = 0 RVA = - 5.71 kN RVA = 5.71 kN 
Resolving forces horizontally∑fX = 0RHA = 0Resolving forces vertically∑fy = 0RVA – 240 + RB = 0RVA + RB = 240 -------------- (1)Taking moment at A∑ MA = 0(240 × 3) – 80 – 6RB = 0640 – 6RB = 0RB = 106.67 kN  Put this value in equation (1)RVA + RB = 240RVA = 240 – 106.67RVA = 133.33 kN
Put this value in equation (1)RVA + RB = 240RVA = 240 – 106.67RVA = 133.33 kN  Q10) Find support reactions for the loading as shown below:
Q10) Find support reactions for the loading as shown below:
Answer 10) Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN
Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN  Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN
Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN 
|
 = 221.843 – 48.31MB = 173.53 N.m Q2) Determine the FR when three forces such as 80 N, 100 N, and 30 N are acting on an object simultaneously and 30 N force is opposite to the other two forces.S2)Given:F1 = 80 NF2 = 100 NF3 = -30 NF3 is a negative value because it is acting opposite to the other two forceThe formula for resultant force isFR = F1+F2+F3FR = 80 + 100 – 30FR = 150 N Q 3) Find support reactions for the loading as shown below:
= 221.843 – 48.31MB = 173.53 N.m Q2) Determine the FR when three forces such as 80 N, 100 N, and 30 N are acting on an object simultaneously and 30 N force is opposite to the other two forces.S2)Given:F1 = 80 NF2 = 100 NF3 = -30 NF3 is a negative value because it is acting opposite to the other two forceThe formula for resultant force isFR = F1+F2+F3FR = 80 + 100 – 30FR = 150 N Q 3) Find support reactions for the loading as shown below:
|
 Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0 Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN
Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0 Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN  Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN
Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN  Q 4) Find the reactions at support A & B.
Q 4) Find the reactions at support A & B.
|
 Resolving forces vertically∑fy = 0RVA – 30 – 80 + RB = 0RVA + RB = 110 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0 Taking moments at A∑ MA = 0(30 × 0.6) + [80 × (4.07 + 0.6)]- (6 × RB) = 018 + 373.6 – 6RB = 06RB = 391.6RB= 65.267 kNPut above value in equation (1)RVA + RB = 110RVA + 65.267 = 110RVA = 110 – 65.267RVA = 44.733 kN Q 5) Explain the different types of beams?A 5) Beam – It is horizontal structural member on which different types of loads can be supported. It takes load from floor or roof & transfers to column.The beam may be sometimes constructed in the inclined position for architectural point of view.Types of Beam: -
Resolving forces vertically∑fy = 0RVA – 30 – 80 + RB = 0RVA + RB = 110 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0 Taking moments at A∑ MA = 0(30 × 0.6) + [80 × (4.07 + 0.6)]- (6 × RB) = 018 + 373.6 – 6RB = 06RB = 391.6RB= 65.267 kNPut above value in equation (1)RVA + RB = 110RVA + 65.267 = 110RVA = 110 – 65.267RVA = 44.733 kN Q 5) Explain the different types of beams?A 5) Beam – It is horizontal structural member on which different types of loads can be supported. It takes load from floor or roof & transfers to column.The beam may be sometimes constructed in the inclined position for architectural point of view.Types of Beam: -
|
(single overhanging beam)
(doubly overhanging beam)
|
|
|
|
|
|

 2Q = 390Q = 195 N &P = 75 N . . . Answer Q 7) Explain the newton’s laws?A 7) Principles of Statics1- Newton’s 1stLaw: -Everybody continues to be in its state of rest or in the state of uniform motion along straight line unless it is acted upon by external unbalanced force.2. Newton’s 2ndLaw:-When unbalanced force acts on particle, it will have an acceleration which is proportional to the magnitude of force. This acceleration will be in the direction of force along straight line.Rate of change of momentum of body is directly proportional to the force acting on it & it is in the direction of force.3. Newton’s 3rdLaw:-Forces of action & reaction between bodies in contact will have same magnitude, line of action but opposite direction. Q 8) What is mechanics explain with classifications?A 8) Mechanics:-The branch of physical science that deals with state of the rest of the motion is called as mechanics.Engineering Mechanics: -The branch of applied science, which deals with laws & Principals of Mechanics along with their applications to the real life engineering problem.Engineering Mechanics is essential for an engineer in Planning, designing & construction of various structures & machines.Classification of Engineering Mechanics: -
2Q = 390Q = 195 N &P = 75 N . . . Answer Q 7) Explain the newton’s laws?A 7) Principles of Statics1- Newton’s 1stLaw: -Everybody continues to be in its state of rest or in the state of uniform motion along straight line unless it is acted upon by external unbalanced force.2. Newton’s 2ndLaw:-When unbalanced force acts on particle, it will have an acceleration which is proportional to the magnitude of force. This acceleration will be in the direction of force along straight line.Rate of change of momentum of body is directly proportional to the force acting on it & it is in the direction of force.3. Newton’s 3rdLaw:-Forces of action & reaction between bodies in contact will have same magnitude, line of action but opposite direction. Q 8) What is mechanics explain with classifications?A 8) Mechanics:-The branch of physical science that deals with state of the rest of the motion is called as mechanics.Engineering Mechanics: -The branch of applied science, which deals with laws & Principals of Mechanics along with their applications to the real life engineering problem.Engineering Mechanics is essential for an engineer in Planning, designing & construction of various structures & machines.Classification of Engineering Mechanics: -  Engineering Mechanics
Engineering Mechanics



 Mechanics of Solids Mechanics of Fluids
Mechanics of Solids Mechanics of Fluids  Mechanics of Rigid Bodies Mechanics of Deformable Bodies
Mechanics of Rigid Bodies Mechanics of Deformable Bodies




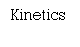
 Statics Dynamics In our syllabus, we are going to study the mechanics of Rigid Bodies i.e. Statics & Dynamics.Statics: -It is the branch of Engineering Mechanics which deals with the forces and their effects (acting) upon the bodies which are at rest.Dynamics: -It is the branch of engineering Mechanics which deals with forces & their effects (acting) upon the bodies which are in motion.Dynamics is again divided into two categories:1. Kinetics2. KinematicsKinetics:-It is the branch of Dynamics which deals with the bodies in motion by considering the forces which cause the motion.Kinematics:-It is the branch of Dynamics which deals with the bodies in motion without considering the force which is responsible for the motion.Mass (m ) :-The quantity of matter possessed by a body,S.I. unit: - gram (g) Kilogram (kg)1 kg = 1000 gWeight (W):-Force acting on the object due to gravity.It is the product of mass & gravitational Acceleration.W = m x gS.I. Unit: - Newton (N)Kilo Newton (KN)1 KN = 1000 N. Q 9) Find the support reactions for given beam. A 9)
Statics Dynamics In our syllabus, we are going to study the mechanics of Rigid Bodies i.e. Statics & Dynamics.Statics: -It is the branch of Engineering Mechanics which deals with the forces and their effects (acting) upon the bodies which are at rest.Dynamics: -It is the branch of engineering Mechanics which deals with forces & their effects (acting) upon the bodies which are in motion.Dynamics is again divided into two categories:1. Kinetics2. KinematicsKinetics:-It is the branch of Dynamics which deals with the bodies in motion by considering the forces which cause the motion.Kinematics:-It is the branch of Dynamics which deals with the bodies in motion without considering the force which is responsible for the motion.Mass (m ) :-The quantity of matter possessed by a body,S.I. unit: - gram (g) Kilogram (kg)1 kg = 1000 gWeight (W):-Force acting on the object due to gravity.It is the product of mass & gravitational Acceleration.W = m x gS.I. Unit: - Newton (N)Kilo Newton (KN)1 KN = 1000 N. Q 9) Find the support reactions for given beam. A 9)
|
 Resolving force horizontally∑fX = 0RHA = 0Resolving forces vertically∑fy = 0RVA + RB = 0 --------------- (1)Taking moments at A
Resolving force horizontally∑fX = 0RHA = 0Resolving forces vertically∑fy = 0RVA + RB = 0 --------------- (1)Taking moments at A 40 – 7RB = 0
40 – 7RB = 0 RB =
RB = 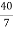 RB = 5.71 kN
RB = 5.71 kN  Put above value in equation (1)RVA + RB = 0RVA + 5.71 = 0 RVA = - 5.71 kN RVA = 5.71 kN
Put above value in equation (1)RVA + RB = 0RVA + 5.71 = 0 RVA = - 5.71 kN RVA = 5.71 kN 
|
 Put this value in equation (1)RVA + RB = 240RVA = 240 – 106.67RVA = 133.33 kN
Put this value in equation (1)RVA + RB = 240RVA = 240 – 106.67RVA = 133.33 kN  Q10) Find support reactions for the loading as shown below:
Q10) Find support reactions for the loading as shown below:
|
 Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN
Resolving forces vertically∑fy = 0RVA – 50 – 20 – 120 + RB = 0RVA + RB = 190 -------------- (1)Resolving forces horizontally∑fX = 0RHA = 0Taking moments at A∑ MA = 0(50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0100 + 80 + 720 – 8RB = 0900 – 8RB = 0RB – 112.5 kN  Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN
Put above value in equation (1)RVA + 112.50 = 190RVA = 77.5 kN 
0 matching results found













