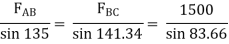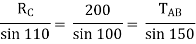EM
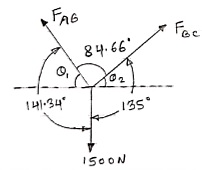
UNIT-3Centroids and Moments of Inertia Q 1) Find the axial force in the bar AB & AC as shown in figure. Consider the free body diagram of all forces at B.
Consider the free body diagram of all forces at B.
Q1 = tan -1 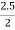 = 51.34ºQ2 = tan-1
= 51.34ºQ2 = tan-1  = 45ºLet the forces developed in the member AB & AC are FAB &FBCrespectively. The force diagram will be as follows at B.
= 45ºLet the forces developed in the member AB & AC are FAB &FBCrespectively. The force diagram will be as follows at B.
Q 2) Find the tensions in the string AB, BC, CD, DE of the given system as shown in figure. String BC is horizontal & pulley D is frictionless.
A 2)  The string passes over the pulley & is attached to weight w = 400 N. Thus TCD = TDE = 400 N Consider joint C & apply Lami’s theorem
The string passes over the pulley & is attached to weight w = 400 N. Thus TCD = TDE = 400 N Consider joint C & apply Lami’s theorem
Now consider FBD at joint B
By using Lami’s theorem 
 TAB = 230.94 N
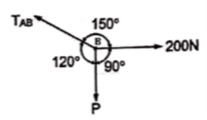
TAB = 230.94 N Q 3) Two identical spheres having weight 1000 N are kept in a container as shown in figure. Find the reaction at all contact surfaces. A 3)
Q 3) Two identical spheres having weight 1000 N are kept in a container as shown in figure. Find the reaction at all contact surfaces. A 3)  Consider the free body diagram of sphere B as shown below:
Consider the free body diagram of sphere B as shown below:
By lami’s theorem 

 RRR = 939.69 N
RRR = 939.69 N
 = RAB Now consider FBD of sphere A
= RAB Now consider FBD of sphere A
∑Fx = 0-RB cos 20 – RQ cos 70 + Rp = 0-342.02 cos 20 – RQ sin 70 + Rp = 0 Rp = 321.39 + 0.34 RQ ------------------(1)∑ fy = 0RQ sin 70 – 342.02 sin 20 – 1000 = 0
Rp = 321.39 + 0.34 RQ ------------------(1)∑ fy = 0RQ sin 70 – 342.02 sin 20 – 1000 = 0 RQ = 1188.66 N - put in equation (1)
RQ = 1188.66 N - put in equation (1) Rp = 725.5 N Q 4) Two members AB & BC are supporting a load of 200 kN as shown in figure. Find the forces developed in the members AB & BC
Rp = 725.5 N Q 4) Two members AB & BC are supporting a load of 200 kN as shown in figure. Find the forces developed in the members AB & BC
 Consider the free body diagram of joint B as shown in figureAssume that member BC is in compression & AB is in tension. By using Lami’s theorem at B,
Consider the free body diagram of joint B as shown in figureAssume that member BC is in compression & AB is in tension. By using Lami’s theorem at B,
-ve sign indicates that member AB is not in Tension but is in compression.Now, 
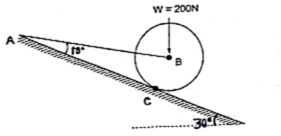
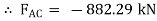 -ve sign indicates that member BC is not in compression but in tension.Q 5) A Spheres of weight 200 N rests on a smooth inclined plane. A sphere is kept in equilibrium by means of cable as shown. Find tension in cable and reaction.
-ve sign indicates that member BC is not in compression but in tension.Q 5) A Spheres of weight 200 N rests on a smooth inclined plane. A sphere is kept in equilibrium by means of cable as shown. Find tension in cable and reaction.
A 5)  Consider the FBD of sphere B as shown in figure above.
Consider the FBD of sphere B as shown in figure above.
Applying lami’s theorem, we have
Q 6) The bar AB supports a load of 500 kN as shown in figure. The bae is kept in equilibrium by means of horizontal rope. Find tension in rope and reaction at A
 Consider the FBD as shown
Consider the FBD as shown
Applying conditions of equilibrium,∑fx = 0RHA – TCD = 0RHA = TCD ------- (1)∑fy = 0RVA – 500 = 0 RVA = 500 kNTaking moment about point A,∑MA = 0-(TCD × 5 ) + (500 × 9) = 0-TCD × 5 = -4500TCD =
RVA = 500 kNTaking moment about point A,∑MA = 0-(TCD × 5 ) + (500 × 9) = 0-TCD × 5 = -4500TCD = 
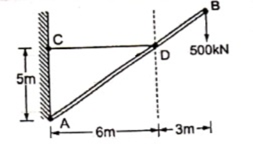
 TCD = 900 kNPutting the value in equation (1)RHA = TCDRHA = 900 kN Q 7) A bar of weight 200 N is hinged at A and pulled by the string attached at B as shown in figure. The length of bar is 5m. Find the support reactions at A & corresponding tension in string.
TCD = 900 kNPutting the value in equation (1)RHA = TCDRHA = 900 kN Q 7) A bar of weight 200 N is hinged at A and pulled by the string attached at B as shown in figure. The length of bar is 5m. Find the support reactions at A & corresponding tension in string.
A 7)  Consider triangle AEC
Consider triangle AEC
Q8) Explain roller supports?A 8)Roller Support: - Roller support is show in two ways as shown: A free body diagram of roller support is shown in figure given below Roller support offers only one reaction; which is always perpendicular to the base or plane of roller. All the steel trusses of the bridges have one of their ends supported on roller. Main advantages of the support are that beam can easily move towards left or right due to expansion & contraction. Q 9) Explain hinge support?A 9) Hinge support
In this case, end of the beam is hinged to the support as shown in figure above. This type of support offers two reactions, one is parallel to base and perpendicular to the base All the steel trusses of the bridges have one of their end roller supported & other end is hinged Main advantage of this support is that beam remains stable. If both ends of the beam are roller supported, then beam cannot be stable. Thus, one support of beam is made roller supported and other is hinged Q 10) Explain the types of beams?A 10) Types of Beam: -Simply supported beam – A beam which is just resting on the supports at the end without any connection is known as simply supported beam. It is generally used for vertical landing system.
2. Overhanging Beam – A beam which is supported at the intermediate point other than ends is called as overhanging beam. Here portion of beam is extended beyond the support
3. Cantilever Beam –A beam which is fixed at one end is called as cantilever beam
Here, there are three reactions components:Vertical reaction at A (RVA) Horizontal reaction at A (RHA) Fixing moment at A (MA) We can assume any direction for above components.4. Continuous Beam:A beam having more than two support is called as continuous beam.
5. Compound Beam:When two or more beams are joined together by using internal hinge; or when one beam rests over another beam by using internal roller, then such beam is called as compound beam.
 Consider the free body diagram of all forces at B.
Consider the free body diagram of all forces at B.
|
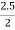 = 51.34ºQ2 = tan-1
= 51.34ºQ2 = tan-1  = 45ºLet the forces developed in the member AB & AC are FAB &FBCrespectively. The force diagram will be as follows at B.
= 45ºLet the forces developed in the member AB & AC are FAB &FBCrespectively. The force diagram will be as follows at B.
FBC = 942.81 N
|
|
 The string passes over the pulley & is attached to weight w = 400 N. Thus TCD = TDE = 400 N Consider joint C & apply Lami’s theorem
The string passes over the pulley & is attached to weight w = 400 N. Thus TCD = TDE = 400 N Consider joint C & apply Lami’s theorem
|
|

 TAB = 230.94 N
TAB = 230.94 N Q 3) Two identical spheres having weight 1000 N are kept in a container as shown in figure. Find the reaction at all contact surfaces. A 3)
Q 3) Two identical spheres having weight 1000 N are kept in a container as shown in figure. Find the reaction at all contact surfaces. A 3)  Consider the free body diagram of sphere B as shown below:
Consider the free body diagram of sphere B as shown below:
|


 RRR = 939.69 N
RRR = 939.69 N
 = RAB Now consider FBD of sphere A
= RAB Now consider FBD of sphere A
|
 Rp = 321.39 + 0.34 RQ ------------------(1)∑ fy = 0RQ sin 70 – 342.02 sin 20 – 1000 = 0
Rp = 321.39 + 0.34 RQ ------------------(1)∑ fy = 0RQ sin 70 – 342.02 sin 20 – 1000 = 0 RQ = 1188.66 N - put in equation (1)
RQ = 1188.66 N - put in equation (1) Rp = 725.5 N Q 4) Two members AB & BC are supporting a load of 200 kN as shown in figure. Find the forces developed in the members AB & BC
Rp = 725.5 N Q 4) Two members AB & BC are supporting a load of 200 kN as shown in figure. Find the forces developed in the members AB & BC
|
 Consider the free body diagram of joint B as shown in figureAssume that member BC is in compression & AB is in tension. By using Lami’s theorem at B,
Consider the free body diagram of joint B as shown in figureAssume that member BC is in compression & AB is in tension. By using Lami’s theorem at B,
|

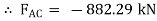 -ve sign indicates that member BC is not in compression but in tension.Q 5) A Spheres of weight 200 N rests on a smooth inclined plane. A sphere is kept in equilibrium by means of cable as shown. Find tension in cable and reaction.
-ve sign indicates that member BC is not in compression but in tension.Q 5) A Spheres of weight 200 N rests on a smooth inclined plane. A sphere is kept in equilibrium by means of cable as shown. Find tension in cable and reaction.
|
 Consider the FBD of sphere B as shown in figure above.
Consider the FBD of sphere B as shown in figure above.
|
|
|
 Consider the FBD as shown
Consider the FBD as shown
|
 RVA = 500 kNTaking moment about point A,∑MA = 0-(TCD × 5 ) + (500 × 9) = 0-TCD × 5 = -4500TCD =
RVA = 500 kNTaking moment about point A,∑MA = 0-(TCD × 5 ) + (500 × 9) = 0-TCD × 5 = -4500TCD = 
 TCD = 900 kNPutting the value in equation (1)RHA = TCDRHA = 900 kN Q 7) A bar of weight 200 N is hinged at A and pulled by the string attached at B as shown in figure. The length of bar is 5m. Find the support reactions at A & corresponding tension in string.
TCD = 900 kNPutting the value in equation (1)RHA = TCDRHA = 900 kN Q 7) A bar of weight 200 N is hinged at A and pulled by the string attached at B as shown in figure. The length of bar is 5m. Find the support reactions at A & corresponding tension in string.
|
 Consider triangle AEC
Consider triangle AEC
EC = 1.61 m Consider triangle AEC
Applying conditions of equilibrium ∑fX = 0 -TBD cos15 + RHA = 0 -------- (1) ∑fy = 0 RVA – 200 – TBD sin15 = 0 RVA – 200 – 0.26TBD = 0 ---------(2) Taking moment at A ∑MA = 0 -(TBD cos15 × 3.2) + (TBD sin15 × 3.84) + (200 × 1.92) = 0 -3.09 TBD + 0.99 TBD + 384 = 0 -2.1 TBD = -384
RVA = 200 + 0.26TBD = 200 + (0.26 × 182.86) RVA = 247.54 N
|
|
|
(singly overhanging beam)
B
(doubly overhanging beam)
|
|
|
|
0 matching results found