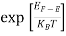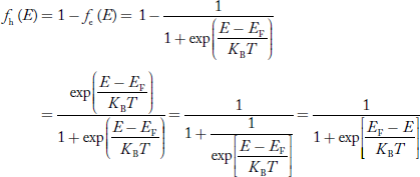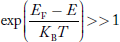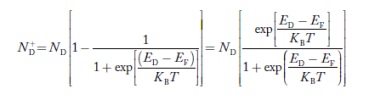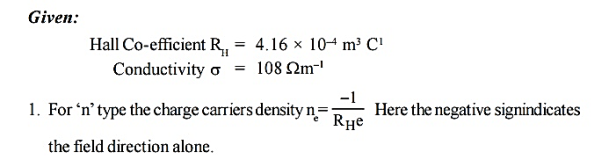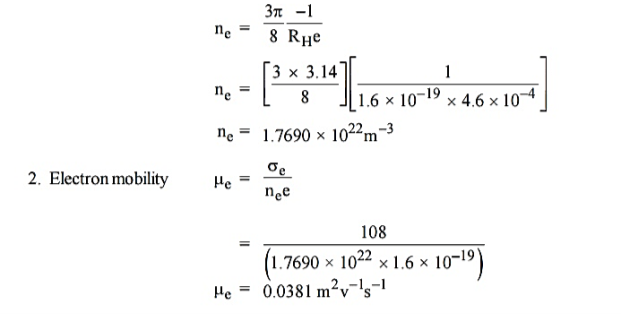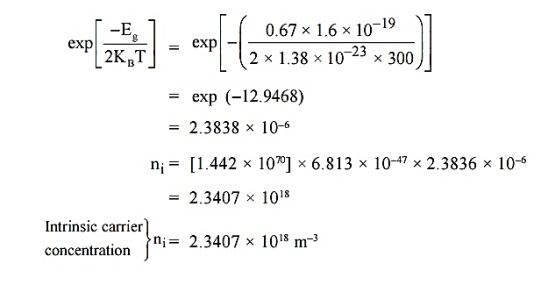undefined | unit 2 semiconductor physics

Back to Study material

UNIT-2SEMICONDUCTOR PHYSICSQ1) For an intrinsic Semiconductor with a band gap of 0.7 eV, determine the position of EF at T = 300 K if m*h = 6m*eA1)

Q2) A semiconducting crystal with 12 mm long, 5 mm wide and 1 mm thick has a magnetic density of 0.5 Wbm–2 applied from front to back perpendicular to largest faces. When a current of 20 mA flows length wise through the specimen, the voltage measured across its width is found to be 37μV. What is the Hall coefficient of this semiconductor?A2)

Q3) Calculate the intrinsic concentration of charge carriers at 300 K given that m *e =0.12m o, m *h =0.28mo and the value of brand gap = 0.67 eV. A 3)

Q4) What do you meant by Built-In Potential?A 4)The Voltage drop across the depletion region under equilibrium conditions, known as the built-in potential (Vbi), is a junction’s parameter of sufficient importance to merit further consideration. We will now find a relationship for Vbi. Consider a non-degenerately doped pn junction maintained under equilibrium conditions with x = 0 positioned at the metallurgical boundary. The ends of the equilibrium depletion region are taken to occur at — xp and xp on the p- and n-sides of the junction respectively We know

…………… (1)

Integrating across the depletion region gives

…………… (2)

Under equilibrium conditions.

…………… (3)

Solving for ξ in equation (3) and making use of the Einstein relationship. We obtain

…………… (4)

Substituting Equation (4) into Equation (2), and completing the integration then yields

…………… (5)

For the specific case of a non-degenerately doped step junction where ND and NA are the n- and p-side doping concentrations, one denies.

…………… (6)

…………… (7)

and therefore

…………… (8)

It is useful to perform a sample computation to gauge the relative magnitude of the built in voltage. Choosing ND= NA = 1015/ cm3 and a Si diode maintained at 300 K,

One computes Vbi= (0.0259) ln(1030/1020) 0.6 V. This is a typical result. In non-degenerately doped diodes Vbi < EG/q, or Vbi is less than the band gap energy converted into volts. Non-degenerately doped Ge, Si, and GaAs diodes maintained at room temperature exhibits a Vbi less than 0.66 V, 1.12 V. and 1.42 V respectively.

From the energy band diagram, we observed

…………… (9)

…………… (10)

…………… (11)

Clearly, for a Non-degenerately doped diode bosh (Ei — EF) p-side, and (EF — Ei) n-side are less than EG/2, making Vbi < EG/q Moreover, in a Non-degenerately doped step junction under equilibrium conditions,

…………… (12)

…………… (13)

Equations (12 and13) and Equation (9) are valid only for Non-degenerately dopings, there are no doping-related restrictions on the validity of Equation (11).Q 5) Define Fermi function also discuss effect of temperature on Fermi functionA 5)Fermi function F (E):Fermi-Dirac distribution function represents the probability of an electron occupying a given energy level at absolute temperature. It is given by

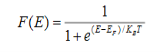Where KB Boltzmann Constant T Temperature If g(E) is the density of states and f(E) gives the probability of occupation of those states at a given temperature, the number of occupied states, n(E), is given by n(E) =

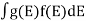(1) If the number of occupied states in an energy band needs to be calculated the integration needs to be performed over the entire band. This will be a function of temperature, since the Fermi function is temperature dependent. Equation 1 can be used to calculate the concentration of electron and holes in semiconductors, which decides their conductivity.Effect of temperature on Fermi Function:Case (i) Probability of occupation for E < EF at T = 0K

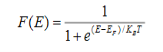When T = 0K and E < EF, we haveF(E) =

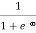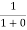= 1Thus at T = 0K, there is 100 % chance for the electrons to occupy the energy levels below the Fermi level.

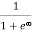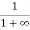Figure 3: Fermi distributionCase (ii) Probability of occupation for E>EF at T = 0K When T = 0K and E > EF, we have F(E) =

= 0Thus, there is 0 % chance for the electrons to occupy energy levels above the Fermi energy level. From the above two cases, at T = 0K the variation of F(E) for different energy values becomes a step function.Case (iii) Probability of occupation at ordinary temperatureAt ordinary temperature, the value of probability starts reducing from 1 for values of E slightly less than EF. With the increase of temperature, i.e., T> 0K, Fermi function F (E) varies with E. At any temperature other than 0K and E = EFF(E) =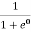

= 50%Hence, there is 50 % chance for the electrons to occupy Fermi level. Further, for E > EF the probability value falls off rapidly to zero. Case (iv) At high temperatureWhen kT >> EF, the electrons lose their quantum mechanical character and Fermi distribution function reduces to classical Boltzmann distribution Q6) Explain Fermi level for intrinsic semiconductors and what is the effect of temperature on Fermi level?A 6)Fermi LevelWe know that in intrinsic semiconductor Electron concentration ‘n’ = Hole concentration ‘p’ Equating Equations (15) and (27), we get

images

Taking logarithms on both sides, we get

……………… (29)

Normally, mh* is greater than me*, since ln

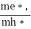is very small so that EF is just lie in the middle of energy gap Temperature effect on Fermi levelFermi level slightly rises with increase of temperature.But in case of pure intrinsic semiconductor like Si and Ge, mh* ≈ me* so in these cases Fermi level lies at the middle of energy gap.Q7) Derive expression for carrier concentration for intrinsic semiconductors? A 7)Intrinsic semiconductors—carrier concentrationHere we will calculate the number of electrons excited into conduction band at temperature T and also the hole concentration in the valence band. It is assumed that the electrons in the conduction band behave as if they are free particles with effective mass me* and the holes near the top of the valence band behave as if they are free particles with effective mass mh*. Here we will calculate the electron concentration, hole concentrationDensity of Electrons in Conduction BandThe number of free electrons per unit volume of semiconductor having energies in between E and E + dE is represented as N(E) dE dE = width of Energy bandTherefore, we have:N(E) dE = ge(E) dE fe (E) ………. (1) ge(E) = The density of electron states per unit volumefe(E) = Fermi-Dirac distribution function i.e. probability that an electron occupies an electron stateThe number of electrons present in the conduction band per unit volume of material ‘n’ is obtained by integrating N(E) dE between the limits Ec and Ect Where Ec = the bottom energy levels of conduction band

Ect = the bottom and top energy levels of conduction band

n = ……….(2)

can be written as

n = =

n = - ……….(3)

we know that above Ect, there is no electrons.

Hence, Equation (3) becomes

n = -

n = ……….(4)

The Fermi-Dirac distribution function fe(E) can be represented as:

(E) = ……….(5)

Compared to the exponential value, so the ‘1’ in the denominator can be neglected.

So >>1

Hence, (E) = = ……….(6)

The density of electron states ge(E) in the energy space from E = 0 to E can be written as:

(E) = [ ]3/2 (E - 0) ½ ……….(7)

where me* is the effective mass of an electron and h is Planck’s constant.

(E)dE = [ ]3/2 (E - 0) ½dE ……….(8)

To evaluate n, the density of states is counted from Ec, since the minimum energy state in conduction band is Ec. so eq (8) can become

(E)dE = [ ]3/2 (E - Ec) ½dE ……….(9)

Substituting Equations (6) and (9) in (4) gives

n = 3/2 (E-)1/2dE

n = [ ]3/2 1/2dE ………… (10)

The above equation can be simplified by the following substitution:

Put ɛ = E − Ec ………… (11)

So, dɛ = dE

In Equation (11), Ec is constant, as we change the variable E to ε in Equation (10), the integral limits also change.

In Equation (11), as E → Ec then ε → 0 and E → ∞, then ε also → ∞.

the exponential term in Equation (10) becomes:

= exp [] = exp []

………… (12)

Substituting Equations (11) and (12) in (10), we get:

n = [ ]3/2 dE

n = [ ]3/2 dE ………… (13)

Above integral (I) can be simplified by substitution. Put ε = x2

so that dɛ = 2x dx

I =2x dx

=dx

= =T)3/2 ………… (14)

Substituting Equation (14) in (13) gives:

n = [ ]3/2T)3/2

n =

n = ………… (15)

The term is almost a constant compared with the exponential term as the temperature changes. So, it is a pseudo constant and is given by the symbol NC. So, we have

n =Nc ………… (16)

Density of Holes in Valence Band

The number of holes per unit volume of semiconductor in the energy range E and E + dE in valence band is represented as P(E) dE. Proceeding same way (as in case of electrons) we have

Therefore, we have:

P(E) dE = gh(E) dE fh(E) ………. (17)

dE = width of Energy band

gh(E) = The density of holes’ states per unit volume

fh(E) = Fermi-Dirac distribution function i.e. probability that a hole occupies an electron state

The number of electrons present in the conduction band per unit volume of material ‘n’ is obtained by integrating P(E) dE between the limits Evb and EV

where EV = the bottom energy levels of valence band

Evb = the bottom and top energy levels of valence band

The total number of holes present in the valence band per unit volume of material ‘p’ is obtained by integrating P(E) dE

………. (18)

Equation (18) can be represented as:

………. (19)

Now we know that below Evb no holes are present. Hence, Equation (19) becomes

………. (20)

We know hole can also be defined as absence of an electron.

presence of a hole = the absence of an electron

Hence, the Fermi-Dirac function of holes fh(E) in the valence band is:

images

Compared to exponential, the ‘1’ in the denominator is negligible,

images

Hence,

………. (21)

The density of hole states between E and E + dE in valence band can be written similar to Equation (8.9) for electrons.

………. (22)

Where mh* is the effective mass of hole.

Substituting Equations (21) and (22) in (20),

………. (23)

The above equation can be simplified by the substitution:

Put ɛ = EV − E ............. (24)

so dɛ = − dE

In Equation (24), EV is constant, as we change the variable E to ε in Equation (23), the integral limits also change.

In Equation (24),

as E → EV then ε → 0

and E→ −∞, then ε → ∞

the exponential term in Equation (23) becomes:

............. (25)

Substituting Equations (24) and (25) in (23), we get:

…………. (26)

From Equation (14), we know the integral value T)3/2 put here and we get

…………. (27)

….The term is almost constant compared with the exponential term as the temperature changes. So, it is a pseudo constant and is given by the symbol NV. So, we have

…………… (28)

Q 8) Where Fermi level lie in case of p type and n type extrinsic semiconductor?OrDerive expression for Carrier Concentration in Extrinsic Semiconductors.A 8)Carrier Concentration in Extrinsic SemiconductorsThe number of charge carriers present per unit volume of a semiconductor material is called carrier concentration. Suppose donor and acceptor atoms are doped in a semiconductor. At temperature T K,n = number of conduction electronsp = number of holes N−A = number of acceptor ions N+D = number of donor ions We know that the below equation hold good in semiconductor. The total negative charge due to conduction electrons and acceptor ions is equal to holes and donor ions in unit volume of material.So the material will be considered neutral if,n + N−A = p + N+D ……….(34) Equation (34) is called charge neutrality equation. In the above equation

………..(35)

concentration of acceptor ions N−A = acceptor concentration x probability of finding an electron in acceptor level

………..(36)

Similarly, the donor ions concentration is

………..(37)

In n-type material Note nn represents electrons in n-type material pn represents holes concentration in n-type material. there are no acceptor atoms so N−A = 0. At 0 K, all the electron states in donor level are occupied by electrons. As the temperature is increased from 0 K, some of the electrons jump from these donor states into the conduction band.Also the concentration of holes is extremely less compared with the concentration of conduction electrons [p << n]From Equation (34) we have n = p N+D(Or) n ≈ N+D …………(38) [since p << N+D]At temperature T K,As the temperature increase Almost all the donor atoms donate electrons to conduction band.

So, in n-type material, the free electron concentration is almost equal to the donor atoms. So we can rewrite the above equation asnn ≈ ND …………….(39)where nn represents electrons in n-type materialalso the hole concentration in n-type material can be obtained by applying law of mass action nn pn =ni2

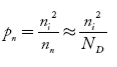…………..(40)where pn represents holes concentration in n-type material. In n-type material at 0 K, the Fermi energy level lies in the middle of Ec and ED images

At temperature> 0K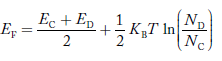

……….(41)With increase in temperature the Fermi level shifts upwards according to Equation (61) slightly due to ionization of donor atoms. 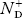With further increase of temperature, electron-hole pairs are generated due to the breaking of covalent bonds, hence Fermi level shifts downwards.In p-type semiconductorNote pp represents holes in p-type materialnp represents electrons in p-type materialThere are no donor atoms so means no ions present images

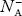= 0. At 0 K, all the acceptor levels are not occupied by electrons. As the temperature is increased from 0 K, some electrons jump from top valence band energy levels to the acceptor states, leaving holes in the valence band and acceptor ions images

are formed. At some room temperature T K, concentration of conduction electrons is extremely less compared with hole concentration.∴ From Equation (34), we have n + N−A = p ……………(42)(or) N−A ≈ p ……………. (43) [since n << N−A]At temperature T K, in p-type material, the hole concentration is almost equal to the acceptor atoms in unit volume of the material. So, Equation (43) can be written aspp ≈ NA ……………….(44)where pp represents holes in p-type materialThe electron concentration in p-type material can be obtained by applying law of mass action as nppp = ni2

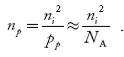…………….(45)where np represent free electron concentration in p-type material.

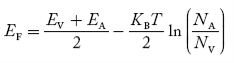In p-type material, the Fermi level lies in between EV and EA at 0 K

As the temperature is increased from 0 K, the Fermi level shifts downwards slightly as per Equation (46) due to ionization of acceptor atoms. And with further increase of temperature, electron-hole pairs are generated due to the breaking of covalent bonds, so Fermi level shifts upwards.Q 9) Derive hall coefficient? Show how hall coefficient and mobility are related? A 9)When the magnetic field is applied perpendicular to a current-carrying conductor, then a voltage is developed in the material perpendicular to both the magnetic field and current in the conductor. This effect is known as Hall Effect and the voltage developed is known as Hall voltage (VH). Hall Effect is useful to identify the nature of charge carriers in material and hence to decide whether the material is an n-type semiconductor or p-type semiconductor, also to calculate carrier concentration and mobility of carriers.Hall Effect can be explained by considering a rectangular block of an extrinsic semiconductor in which current is flowing along the positive X-direction and magnetic field B is applied along Z-direction as shown in Figure.

11 Figure: Hall EffectSuppose if the semiconductor is n-type, then mostly the carriers are electrons and the electric current is due to the drifting of electrons along negative X-direction or if the semiconductor is p-type, then mostly the carriers are holes and the electric current is due to drifting of the holes along positive X-direction. As these carriers are moving in the magnetic field in the semiconductor that means they experience Lorentz force represented by FLFL = Bevd Where vd is the drift velocity of the carriers. (already explained in the previous section).We can obtain the direction of this force by applying Fleming’s left-hand rule in electromagnetism.Fleming’s left-hand rule can be explained as If we stretch the thumb, forefinger, and middle finger in three perpendicular directions so that the forefinger is parallel to the magnetic field and the middle finger is parallel to the current direction, then the thumb represents the direction of the force on the current-carrying carriers. So the Lorentz force is exerted on the carriers in the negative Y-direction. Due to Lorentz force, more and more carriers will be deposited at the bottom face (represented by face 1in the figure) of the conductor. The deposition of carriers at the bottom face is continued till the repulsive force due to accumulated charge balances the Lorentz force. After some time of the applied voltage, both the forces become equal in magnitude and act in opposite direction, then the potential difference between the top and bottom faces is equal to Hall voltage and that can be measured.At equilibrium, the Lorentz force on a carrier FL = Bevd ……………..(1)and the Hall force FH = eEH ……………..(2)Where EH is the Hall electric field due to accumulated charge.At equilibrium, FH = FLeEH = Bevd∴ EH = Bvd ……………..(3)If ‘d’ is the distance between the upper and lower surfaces of the slab, then the Hall fieldEH =

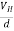……………..(4)In n-type material, Jx = –nevdvd = -

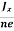……………..(5)Where n is free electron concentration, substituting (5) in (3), we have ∴ EH = -B

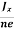……………..(6)For a given semiconductor, the Hall field EH is proportional to the current density Jx and the intensity of magnetic field ‘B’ in the material.i.e. EH ∝ JxB(or) EH = RHJxB ……………..(7)Where RH = Hall coefficientEquations (6) and (7) are the same so, we haveRHJxB =-B

RH = -

= -

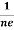……………..(8)Where ρ is the charge density Similarly for p-type materialRH =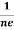

……………..(9)Using Equations (8) and (9), carrier concentration can be determined.Thus, the Hall coefficient is negative for n-type material. In n-type material, as the more negative charge is deposited at the bottom surface, so the top face acquires positive polarity and the Hall field is along negative Y-direction. The polarity at the top and bottom faces can be measured by applying probes. Similarly, in the case of p-type material, a more positive charge is deposited at the bottom surface. So, the top face acquires negative polarity and the Hall field is along positive Y-direction. Thus, the sign of the Hall coefficient decides the nature of (n-type or p-type) material. The Hall coefficient can be determined experimentally in the following way:Multiplying Equation (7) with ‘d’, we haveEHd = VH = RHJxBd ……………..(10)From (Figure 15) we know the current density JxJx =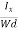

Where W is the width of the box. Then, Equation (10) becomesVH = RH

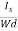Bd = RH

RH =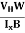

……………..(11)Substituting the measured values of VH, Ix, B, and W in Equation(11), RH is obtained. The polarity of VH will be the opposite for n- and p-type semiconductors.The mobility of charge carriers can be found by using the Hall effect, for example, the conductivity of electrons isn = neμnOr we can rewrite it asμn =

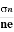=n RH ……………..(12)by using equation (11)μn = n

……………..(13)Q10) Discuss the application of the Hall Effect?A 10)• Using magnetic flux leakage – To properly inspect items such as pipes or tubes, Hall Effect probes work with something called magnetic flux leakage. This is a way of testing such items, and being able to spot potential corrosion, erosion, or pitting. This is specifically used in steel items and can give important information about lifespan or safety.• Sensors to detect rotation speed – A Hall Effect probe can be used in bicycle wheels, speedometers in the automotive world, electronic types of ignition systems, and gear teeth.• Used to detected movement – You will often find a Hall Effect probe used in such items as Go-Kart controls, smartphones, paintball guns, or airsoft guns, as well as some GPS systems.• Ferrite Toroid Hall Effect current transducers – This is mainly used in electronic compasses, making use of the magnetic field to show direction.• Split-ring clamp-on sensors – These types of Hall Effect probes are used to test equipment without having to take the whole circuit board apart, e.g. complex items.• Analog multiplication – Anything which needs a power measurement, e.g. sensing, and is also used in small computers.• General power measurement – Any device which needs to be tested for its power input can be done by a Hall Effect probe.• Position and motion sensors – This is mainly used in a DC motor, often the brushless type.• The automotive world – Hall Effect probes are used widely in the automotive world, especially in fuel injection and ignition. Wheel rotation sensors also use Hall Effect probes, e.g. for anti-lock braking.

For determination of the type of given semiconductor.

For N-type, Hall coefficient RH= negative
For P-type, Hall coefficient RH= Positive

To determine carrier concentration n and p; that is n=p=1/e𝑅𝐻

Determination of mobility of charge carriers μn =

=n RH. Where 𝜎= electrical conductivity

To determine the sign of charge carriers whether the conductivity is due to electrons or holes.

Main Advantages of Using Hall SensorsWhy is a Hall Effect probe advantageous in all of these instances? Because the probes are not affected by outside influences, e.g. water or dirt. They can also easily sense the measure of the output they need when they are placed in the right position. On top of this, Hall Effect probes are safer, because the voltage never actually makes it directly to the sensor/probe. This makes this type of measurement overall so much safer than other methods.As you can see, understanding how something is put into practice in the real world helps you to understand it in real terms. The Hall Effect is certainly very commonplace these days, in much more methods and applications than we realize. While certainly very useful in the automation world, even basic items such as a compass make large use of this scientific approach.Q 11) The Hall coefficient of certain silicon specimen was found to be –7.35 × 10–5 m3 C–1 from 100 to 400 K. Determine the nature of the semiconductor. If the conductivity was found to be 200 –1 m–1. Calculate the density and mobility of the charge carrier. A 11)

Q12) An N-type semiconductor has hall coefficient = 4.16 × 10–4 m3 C–1. The conductivity is 108 m–1. Calculate its charge carrier density ‘ne’and electron mobility at room temperature. A 12)

Q13) In an N-type semiconductor, the concentration of electron is 2 × 1022 m–3. Its electrical conductivity is 112 m–1. Calculate the mobility of electrons. A 13)

Q14) Calculate the intrinsic concentration of charge carriers at 300 K given that m *e =0.12m o ,m *h =0.28mo and the value of brand gap = 0.67 eV. A 14)

Q15) Explain Bipolar junction transistor its type and working?A 15) Bipolar junction transistor or BJT is simply known as Transistor. A transistor consists of two pn junctions formed by sandwiching either p-type or n-type semiconductor between a pair of opposite types.The prefix 'trans' means the signal transfer property of the device while 'istor ' classifies it as a solid element in the same general family with resistors. Accordingly there are two types of transistors

n-p-n transistor

p-n-p transistor

An n-p-n transistor is composed of two n-type semiconductors separated by a thin section of p-type as shown in Figure 1 (i). However, a p-n-p transistor is formed by two p-sections separated by a thin section of n-type as shown in Figure 1(ii).

Figure1: (i) n-p-n transistor (ii) p-n-p transistorIn each type of transistor, the following points may be noted: (i) Transistor may be regarded as a combination of two diodes connected back to back. (ii) There are three terminals, one taken from each type of semiconductor. (iii) The middle section is a very thin layer. The thin layer plays an important role in the function of a transistor. A transistor has two pn junctions. one junction is forward biased and the other is reverse biased. The forward biased junction has a low resistance path whereas a reverse biased junction has a high resistance path. The weak signal is introduced in the low resistance circuit and output is taken from the high resistance circuit. Therefore, a transistor transfers a signal from a low resistance to high resistance. A transistor (pnp or npn) has three sections of doped semiconductors. The section on one side is the emitter and the section on the opposite side is the collector. The middle section is called the base and forms two junctions between the emitter and collector.

Figure 2: (i) p-n-p transistor (ii) n-p-n transistorEmitter: The section on one side that supplies charge carriers (electrons or holes) is called the emitter. The emitter is always forward biased w.r.t. base so that it can supply a large number of majority carriers. In Figure 2 (i), the emitter (p-type) of pnp transistor is forward biased and supplies hole charges to its junction with the base. Similarly, in Figure 2 (ii), the emitter (n-type) of npn transistor has a forward bias and supplies free electrons to its junction with the base. Collector: The section on the other side that collects the charges is called the collector. The collector is always reverse biased. Its function is to remove charges from its junction with the base. In Figure 2 (i), the collector (p-type) of pnp transistor has a reverse bias and receives hole charges that flow in the output circuit. Similarly, In Figure 2 (ii), the collector (n-type) of npn transistor has reverse bias and receives electrons. Base: The middle section which forms two pn junctions between the emitter and collector is called the base. The base emitter junction is forward biased allowing low resistance for the emitter circuit. The base-collector junction is reverse biased and provides high resistance in the collector circuit. Before studying action of transistor, some important facts about transistor should be keep in mind.

The transistor has two pn junctions i.e. it is like two diodes. The junction between emitter and base may be called emitter-base diode or simply the emitter diode. The junction between the base and collector may be called collector-base diode or simply collector diode.

The emitter diode is always forward biased whereas collector diode is always reverse biased.

Three regions of transistor are emitter, base and collector. The base is much thin as compared to emitter while "collector is wider than both. To keep it simple it is assumed emitter and collector is considered to be of same size.

The emitter is heavily doped so that it can inject a large number of charge carriers (electrons or holes) into the base. The base is lightly doped and very thin it passes most of the emitter injected charge carriers to the collector. The collector is moderately doped.

The resistance of emitter diode (forward biased) is very small as compared to collector diode (reverse biased). Therefore, forward bias applied to the emitter diode is generally very small whereas reverse bias on the collector diode is much higher.

Working of Transistor (i) Working of npn transistor: As discussed in the npn transistor emitter-base junction is forward biased to emitter-base junction and collector-base junction is reverse biased. The forward bias causes the electrons in the n-type emitter to flow towards the base. This constitutes the emitter current Ie. Ie = Ib + Ic

Figure 3: n-p-n transistorAs these electrons flow through the p-type base, they tend to combine with holes. As the base is lightly doped and very thin, therefore, only a few electrons (less than 5%) combine with holes to constitute base current Ib. The remainder i.e. more than 95% cross over into the collector region to constitute collector current Ic In this way, almost the entire emitter current flows in the collector circuit. It is clear that emitter current is the sum of collector and base currents i.e.(ii) Working of pnp transistor: In the pnp transistor emitter-base junction is forward biased to emitter-base junction and collector-base junction is reverse biased. The forward bias causes the holes in the p-type emitter to flow towards the base. This constitutes the emitter current Ie. As these holes cross into n-type base, they tend to combine with the electrons. As the base is lightly doped and very thin, therefore, only a few holes (less than 5%) combine with the electrons.

Figure 4: p-n-p transistorThe remainder (more than 95%) cross into the collector region to constitute collector current Ic. In this way, almost the entire emitter current flows in the collector circuit. It may be noted that current conduction within pnp transistor is by holes. However, in the external connecting wires the current is still by electrons. Thus the input circuit (i.e. emitter-base junction) has low resistance because of forward bias whereas output circuit (i.e. collector base junction) has high resistance due to reverse bias. As we have seen, the input emitter current almost entirely flows in the collector circuit. Therefore, a transistor transfers the input signal current from a low resistance circuit to a high-resistance circuit.Q16) Discuss the type of Bipolar Junction Transistor’s Configuration? A 16) Transistor’s Configuration:- 1) Common Base configuration(C.B)2) Common emitter Configuration(C.E)3) Common Collector Configuration(C.C) COMMON BASE CONFIGURATION

The notation and symbols of pnp and npn transistors are given below:

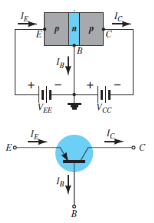
Description: pnp_Cb.png Description: npn_cb.png

Figure 5: PNP CB and NPN CB (Ref. 2)

Here the base is common to both the input and output sides of the configuration.

The flow of holes will govern the direction of current.

Hence, Ic = Ib + Ie

Where Ic, Ib, Ie are the collector, base and emitter currents respectively.

The graphical symbol of the PNP common base configuration is

Description: cb_sym.png

Figure 6 : PNP common base(Ref. 2)

The arrow in the above symbol shows the direction of emitter current in the device.

Now, to study the behavior of the device we require two characteristics:

Input Characteristic Curve

Description: cb_inp.png

Figure 7: Input Characteristic Curve (Ref. 2)

It is the relation between the input current IE to the input voltage VBE for various levels of output voltage VCB.

It is also known as driving point characteristics.

Output Characteristic Curve

Description: cb_out.png

Figure 8: Output Characteristic Curve (Ref. 2)

It is the relation between the output current IC to the output voltage VCB for various levels of input current IE.

It is also known as collector set of characteristics.

It has three basic regions:

Active Region

Here, base-emitter junction is forward biased and collector-base junction is reverse biased.

As input current IE increases above zero, output current IC increases to a magnitude equal to IE as determined by the basic transistor current relationship.

So the first approximation determined by the curve is

IC ≈ IE2. Cut-off Region

It is defined as the region where the collector current IC is equal to 0A.

Here, the base-emitter junction and the collector-base junction both are in reverse bias.

3. Saturation Region

It is the region that lies towards the left of VCB = 0V.

Here, the base-emitter junction and the collector-base junction both are in forward bias.

COMMON EMITTER CONFIGURATIONThe notation and symbols of npn and pnp transistors are given below:

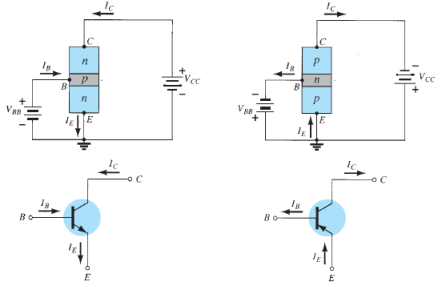
Description: ce.png

Figure 9: NPN CE and PNP CE (Ref. 2)

In the above figure all the currents are shown in their actual conventional directions.

The current relation developed earlier is still applicable,

IE = IB + ICWhere IE , IB , IC are the collector, base and emitter currents respectively.

The graphical symbol of the PNP common emitter configuration is

Description: ce_sym.png

Figure 10: PNP common emitter (Ref. 2)

Now, to study the behavior of the device we require two characteristics:

Input Characteristic Curve

Description: ce_in.png

Figure 11: Input Characteristic Curve (Ref. 2)

It is the graph between the input current IB to the input voltage VBE for a range of values of output voltage VCE.

Note that the magnitude IB of is in micro amperes and that of IC is in milli amperes.

Output Characteristic Curve

Description: ce_out.png

Figure 12: Output Characteristic Curve (Ref. 2)

It is the graph between the output current IC to the output voltage VCE for a range of values of input current IB.

It has three basic regions:

Active Region

Here, the base-emitter junction is forward biased and collector base junction is reverse biased.

These are the same conditions that existed in the active region of the common base configuration.

This can be employed for voltage, current or power amplification.

Cut-off Region

Here IC is not equal to zero when IB is zero.

For linear amplification purposes, it is defined as IC = ICEO .

The region below IB = 0µA is to be avoided for undistorted output signal.

When the transistor is used as a switch, the condition should be ideally IC = 0mA for a chosen VCE voltage.

Saturation Region

It is the region that lies towards the left of VCE = 0V.

COMMON COLLECTOR CONFIGURATIONThe notation and symbols of npn and pnp transistors are given below:

Description: cc.png

Figure 13: NPN CC and PNP CC (Ref. 2)

In the above figure all the currents are shown in their actual conventional directions.

It is used for impedence matching purposes as it has high input impedence and low output impedence.

It can be designed using common emitter characteristics.

The output characteristics of common collector is same as that of common emitter configuration for all practical purposes.

The output characteristics are a plot between IE versus VCE for all values of IB.

The input current of common collector is same as that of common emitter configuration.

Here the region of operation will ensure that maximum ratings are not being exceeded and output ratings have minimum distortion.

Description: cc_curve.png

Figure 14: Output Characteristic Curve (Ref. 2)

The characteristics specifying the minimum VCE that can be applied without entering the non-linear region is saturation region.

The maximum power dissipation is given by,

P = VCE . ICComparison of configuration :

Sr.no	Parameter	CB	CE	CC
1	Common terminal betnI/p & o/p	Base	Emitter	collector
2	Input Current	IE	IB	IB
3	Output Current	IC	IC	IE
4	Current Gain	=	=	ɤ==1
5	Input Vtg.	VEB	VBE	VBC
6	Output Vtg.	VCB	VCE	VCC

Sign Up