As we don’t know perpendicular distance betn force & point ‘ B ’, Let us resolve the force into two components.
Fx = 90 Cos 25 = 81.567 N Y – Component of force Fy = 90 Sin 25 = 38.036 Now taking moments about point B. MB = [Fx x (3 Sin 65)] - [Fy x (3 Cos 65)] MB = (81.65 x 2.72) – (38.036 x 1.27)
MB = 173.53 N.m
|
Given: F1 = 80 N F2 = 100 N F3 = -30 N F3 is a negative value because it is acting opposite to the other two force The formula for resultant force is FR = F1+F2+F3 FR = 80 + 100 – 30 FR = 150 N |
|
∑fy = 0 RVA – 50 – 20 – 120 + RB = 0 RVA + RB = 190 -------------- (1) Resolving forces horizontally ∑fX = 0 RHA = 0
Taking moments at A ∑ MA = 0 (50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0 100 + 80 + 720 – 8RB = 0 900 – 8RB = 0 RB – 112.5 kN Put above value in equation (1) RVA + 112.50 = 190 RVA = 77.5 kN
|
|
∑fy = 0 RVA – 30 – 80 + RB = 0 RVA + RB = 110 -------------- (1) Resolving forces horizontally ∑fX = 0 RHA = 0
Taking moments at A ∑ MA = 0 (30 × 0.6) + [80 × (4.07 + 0.6)]- (6 × RB) = 0 18 + 373.6 – 6RB = 0 6RB = 391.6 RB= 65.267 kN Put above value in equation (1) RVA + RB = 110 RVA + 65.267 = 110 RVA = 110 – 65.267 RVA = 44.733 kN
|
Beam – It is horizontal structural member on which different types of loads can be supported. It takes load from floor or roof & transfers to column. The beam may be sometimes constructed in the inclined position for architectural point of view. Types of Beam: -
A beam which is just resting on the supports at the end without any connection is known as simply supported beam. It is generally used for vertical landing system.
2. Overhanging Beam – A beam which is supported at the intermediate point other than ends is called as overhanging beam. Here portion of beam is extended beyond the support
(single overhanging beam)
b)
(doubly overhanging beam)
3. Cantilever Beam – A beam which is fixed at one end is called as cantilever beam
Here, there are three reactions components:
We can assume any direction for above components. 4. Continuous Beam:
A beam having more than two supports is called as continuous beam.
5. Compound Beam:
When two or more beams are joined together by using internal hinge; or when one beam rests over another beam by using internal roller, then such beam is called as compound beam.
|
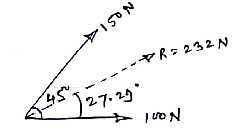
Q = 150 N θ = 45o R =? α=? Solution: According to law of parallelogram of force, R = √ P2 + Q2 + 2PQ Cos θ R = √ 1002 + 1502 + 2 x 100 x 150 x Cos 450 R = 231.76 N R ≈ 232 N - - - Answer - - - magnitude tanα = Q Sin θ / P + Q Cos θ = 150 Sin 450 / 100 + 150 Cos 450 = 106.066 / 206.066 α = 27.290. . . . . Direction
|
Given:
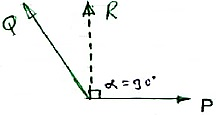
R = 180 N α = 900 Solution : According to law of parallelogram, Tanα = Q Sin θ / P + Q Cos θ Tan 90 = Q Sin θ / P + Q Cos θ ∞ = Q Sin θ / P + Q Cos θ Here if P + Q Cos θ = 0, then only above term will become infinity. Thus, P + Q Cosθ= 0 P = - Q Cos θ -P = Q Cosθ . . . . (1) Now, R2 = P2 + Q2 + 2PQ Cos θ 1802 = P2 + Q2 + 2P (-P) . . . from equation (1) 1802 = P2 + Q2 + (-2P2) 1802 = P2 -2P2 + Q2 1802 = - P2 + Q2 1802 = Q2 - P2 1802 = (Q- P) (Q+ P) = (Q- P) x 270 Q- P = 1802 / 270 Q- P = 120 . . . (ii) & we know that Q + P = 270 . . . (iii) Solving (ii) & (iii) i.e. add eqn (ii) & (iii) Q – P = 120 + Q + P = 270 _______________ 2Q + 0 = 390
Q = 195 N &P = 75 N . . . Answer
|
|
∑fX = 0 RHA = 0 Resolving forces vertically ∑fy = 0 RVA + RB = 0 --------------- (1) Taking moments at A
RB = 5.71 kN Put above value in equation (1)
RVA + 5.71 = 0 RVA = - 5.71 kN RVA = 5.71 kN
Resolving forces horizontally ∑fX = 0 RHA = 0 Resolving forces vertically ∑fy = 0 RVA – 240 + RB = 0 RVA + RB = 240 -------------- (1) Taking moment at A ∑ MA = 0 (240 × 3) – 80 – 6RB = 0 640 – 6RB = 0 RB = 106.67 kN Put this value in equation (1) RVA + RB = 240 RVA = 240 – 106.67 RVA = 133.33 kN
|
|
∑fy = 0 RVA – 50 – 20 – 120 + RB = 0 RVA + RB = 190 -------------- (1) Resolving forces horizontally ∑fX = 0 RHA = 0 Taking moments at A ∑ MA = 0 (50 × 2) + (20 × 4) + (120 × 6) – 8RB = 0 100 + 80 + 720 – 8RB = 0 900 – 8RB = 0 RB – 112.5 kN Put above value in equation (1) RVA + 112.50 = 190 RVA = 77.5 kN
|