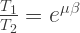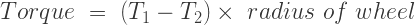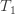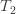undefined | unit 2 analysis of perfect frames

Back to Study material

UNIT - 2Analysis of Perfect FrameQ1) Explain simple and compound machine?A1) Simple Machine A machine a device by which heavy load can be lifted by applying less effort as compared to the load. Eg. Heavy load of car can be lifted with the help of simple screw jack by applying small force.Compound Machine: Compound machine is a device which may consists of number of simple machines. A compound machine may also be defined as a machine which has multiple mechanisms for the same purpose. Compound machines do heavy work with less efforts and greater speed. e.g. In a crane, one mechanism (gears) are used to drive the rope drum and other mechanism (pulleys) are used to lift the load. Thus, a crane consists of two simple machines or mechanisms i.e. gears and pulleys. Hence, it is a compound machine. Q2) What is efforts and load?A2) Effort: It may be defined as, the force which is applied so as to overcome the resistance or to lift the load. It is denoted by „P‟. Magnitude of effort (P) is small as compared to the load (W). Load: The weight to be lifted or the resistive force to be overcome with the help of a machine is called as load (W). Q3) Explain reversible and irreversible machine?A3) Reversible Machine: When a machine is capable of doing some work in the reverse direction even on removal of effort, it is called as reversible machine. Condition for Reversible Machine: The efficiency of the machine should be more than 50%. Irreversible Machine / Non-reversible Machine / Self Locking Machine: When a machine is not capable of doing some work in the reverse direction even on removal of effort, it is called as irreversible machine or non-reversible machine or self-locking machine. Condition for Irreversible Machine: The efficiency of the machine should be less than 50%. Q4) Explain static and kinetic friction?A4) A) Static Friction. In order to set in motion a body lying on an even surface in aState of rest, a critical force, the force of static friction Fs, must be overcome. ThisForce is roughly proportional to the normal force FN 1:Fs = μs N F.The coefficient μs is called the coefficient of static friction. It is dependent on thePairing of the contacting materials, however, shows almost no dependence on contact area or roughness. B. Kinetic Friction FR is the resisting force which acts on a body after the Force of static friction has been overcome. Coulomb experimentally determined the following properties of kinetic friction:Kinetic friction is proportional to the normal force FN:FR = μk N F It shows no considerable dependence on the contact area or roughness of theSurface.The coefficient of kinetic friction is approximately equal to the coefficient ofStatic friction:μk s ≈ μ This proportionality is known as Amontons’ law.Q5) Determine the forces in each member of the plane truss as shown in fig. in terms pf the external loading and state if the members are in tension or compression. Use 0+ 30 deg, L = 2 m and p =100N.Diagram

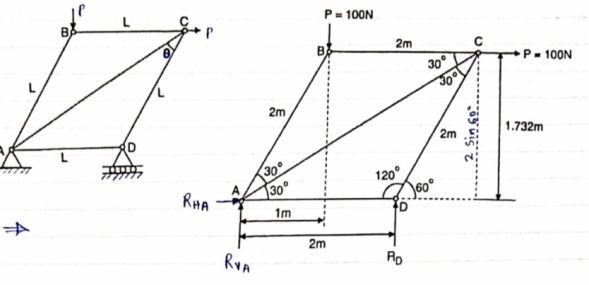
Description: IMG_20191220_205910.jpg

A5)

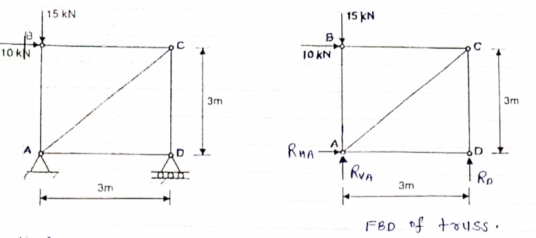
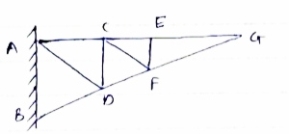
Consider FBD of Truss,

For equilibrium, Fx =0

RHA+100 =0

RHA =-100 KN

Fy =0 RVA = RD – 100 ….. 1

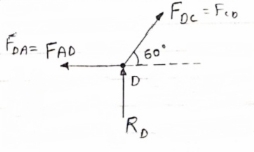
MA = 0 -------Taking moment @ A

- (Roxz) + (100*1) + (100*1.732) =0

- - 2 Rd + 100 + 1.7320 =0

- -2 Rd + 100 + 173.2 =0

- RD =136.66 N ()

From eqn (1)

RVA = 100 – 136.6

RVA= 36.6N

RVA = 36.6 N

Consider Joint D, for equilibrium,

Fx =0

-FAD + FCD cos 60 =0 – (11)

Fy = 0

136.6 +FCD sin 60 +0 Description: IMG_20191220_210201.jpg

FCD = -157.73 N ©

From eqn (11), Fad =- 78. 87 N (c)

Consider point A, for the equilibrium of point A,

Fx = 0

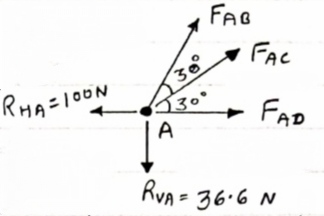
- 100 + FAD + FAc cos + 30 FAb cos60 = 0

-100 + (-78.87) +FAC cos 30 +FAb cos60 =0

FAc cos 30 + FAB cos60 + 178. 87 (3)

Description: IMG_20191220_210453.jpg

fx =0

-36.6 + FAC sin 30 + FAB sin 60 =0

FAC sin 30 + FAb sin 60 = 36.6

Solving eqn (3) and (4)

FAC = 273.21 N (T)

FAB = -115.47 N

FAB= 115.47 N ©

Consider point B, for the equilibrium of point,

Fx =0

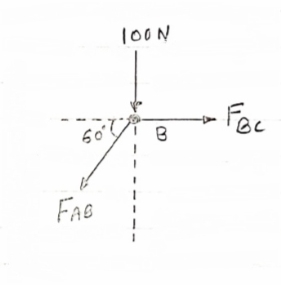
-FAB cos60 + FBC =0

-[9-115.47) cos60]+ FBC =0

Description: IMG_20191220_210331.jpg

FBC = -57.73 N

FBC =57.73N

Member	AB	BC	CD	AD	AC
Force	115.47N	57.73N	157.73N	78.87N	273.21N
Nature	c	C	c	c	T

Q6) Determine the axial forces in each member of the plane truss as shown in figure.

Description: IMG_20191220_210955.jpg

A6)

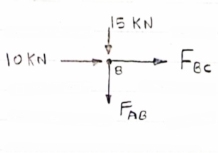
Consider FBD of Truss,

For the equilibrium of Truss, fx =0

RHA + 10 =0

RHA = -10 KN

RHA =10KN (

Resolving forces vertically,

fy =o

RVA + RD -15 =0

RVA + RD = 15 …… (1)

Taking moment about point A,

Fy =0

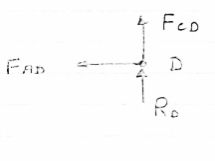
(10*3) – 3 Rd =0

30+ 3 Rd =0

RD= 10 KN

RVA = 5KN ()

Now Consider joint B, FBD of joint B is shown below.

Assuming forces developed in all members to be Termile,

For the equilibrium of joint We have

fx =0

10+FBC =0 Description: IMG_20191220_211045.jpg

FBC = -10 KN

FBC = 10KN (c)

fy =0

FAB = -15 KN

FAB = 15 KN (c)

Now consider joint c,

For the equilibrium of joint,

fx =0

-FBC – FAC cos 45 =0

- (-10) – FAC cos 45=0

10= FAC cos 45

FAC = 10/cos 45 Description: IMG_20191220_211148.jpg

FAc = 14.14 KN (T)

fy =0

-Fac sin 45 – FCD=0

- 14.14 sin45 = FCD

FCD = -10 KN (c)

FCD= 10 KN (c)

Consider joint D,

By observation,

FAD=0

Description: IMG_20191220_211300.jpg

Sr .No	Member	Force	Nature
1	AB	15 KN	c
2	BC	10KN	c
3	CD	10KN	c
4	DA	0	-
5	AC	14.14	T

Q7) Explain the difference between frame and truss?A7)

Difference between Frame and Truss:

Truss

Stationary structure which consist of only two force members.
All joint are pin joints
Load are applied at the joint only
For analysis FBD of each joint is considered

Frame

Stationary structure which consist of various members out of which at least one must be multi force members
Here also all joint are pins.
Load are applied anywhere on the members
For analysis FBD of each members is considered

Q8) Explain single band brake?A8)

Simple Band Brake:

Friction can be used as a power-transmitting agent (in belts-pulleys) as well as a power-absorbing agent (in band brakes). The idea is, the band resists the motion of rotating wheel through friction. The braking torque is obtained by the relations

${\frac {T_1}{T_2} = e^{\mu \beta}}$