undefined | unit 4 kinematics and kinetics of particles

Back to Study material

UNIT-4Kinematics & Kinetics of ParticlesQ1) A projectile is fired with a velocity of 60 m/s on Horizontal plane. Find its time of flight in the following 3 cases.a) is Range is 4 times the max . Heightb) Its max height is 4 times Horizontal range.c) Its max. Height & Horizontal range are equal.A1)

u = 60m/s

a) When R = 4 H

u2 sin 2 /g=4 [ 4 2.sin2/2g]

:. u2/g 2sincos = 242/g sin2

:. Cos = sin

:. Cos - sin =o:. = 45

Time of flight t= 2usin /g = 2* 60* sin 45/9081 = 8.65 sec.

b) When H = 4R

:. u2sin2/2g = 4[ 42 sin 2/g]

:. Sin2 = 8 sin 2

:. sin=(2*8) cos

:. sin = 16 cos

:. tan= 16 & = 86.42

t= 2usin/g = 2*60*sin86.42/9.81 = 12.21 sec

c) When H = R

u2sin2/ 2g = u2 sin2g :. Sin2 /2 = sin2

: .Sin2 = 2*2 sin cos

:. Sin = 4 cos

:.tan =4 :.= 75.96

t= 2usin /g

= 2*60*sin75.96/9.81

t = 11.87 sec.

Q2) A projectile is aimed at an object Qn a H.p through the point of projection and tall 8 M 8 short when the angle of projection is 15

, while it overshoots the the object by 18 m when the angle of projection is 45

Determine the angle of projection to Hit the object exactly.A2)

Let R = actual Range required to hit the object.

ax I - =15

Range = R -8

:. u2* sin (2*15)/g = (R-8)

:. Multiply both sides by 2

:. 2/g = 2R-16-------- (1)

Cos (2) =45

Range = R +18

u2 sin2/g = R+18

u2/g. sin 90 = R +18

:. 42/g = R =18------------ (2)

From (1) & (2) R +18 = 2 R- 16

:. 2R – R = 18+16 = 34.

:. 2R = 34m ---- Actual Range to hit the object

Actual Range

R (42/g) sin 2

34 = (R +18) sin2

34 = (34+18) sin2

34 = 52 sin 2

:. Sin 2= 0.653

= 20.38 - Angle of projection to hit the object

Q3) A shot is fired from the gun .After 2 sec. the velocity of shot is inclined at 30

up the horizontal After 1 more second. It attains max height. Determine the initial velocity and angle of projection.A3)

Let, u = initial velocity = angle of projection. Let, after. 2 second, the shot fired from gun reaches at point D Here Vo makes 30 angle with Horizontal.

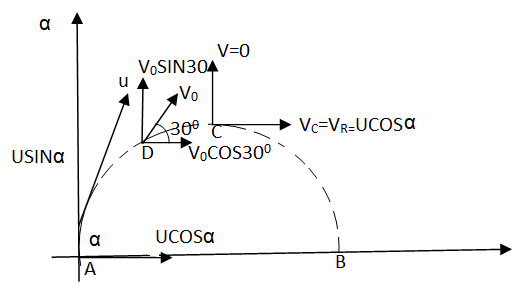
$C:\Users\Ssd\Desktop\UNIT 1 1.png$ & Let after one more second, shot attains max , Height at point C as shown in figure.

At point D, V0 makes 30 with Horizontal.

:. X component of velocity at ‘D’ = VD cos 30

But we know that velocity in X dirn is constant (U.m.)

:. VD cos 30 = u cos

:. 0.87 VD cos 30 = ucos ---- (1)

Consider y-Motion from A to D. By substituting the value of VD ineqn (1) & (2)

This is Motion under gravity 0.87 VD = u cos

:. V = u +at : U cos = 0.87*19.62

:. VD sin 30 = usin- gtAD : ucos = 0.87* 19.62

:. 0.5 VD = usin- 9.81*2 : ucos=17.069 m/s – (3)

:.0.5 VD = usin- 19.62 – (2)

Now

Consider y motion from D-c , (M.V.G) Also, usin= 0.5VD + 19.62

V = u +at = 0.5*19.62+ 19.62

0 = VD sin30 – g*tDC =u sin= 29.43 m/s & -------- (4)

0= 0.5 VD – 9.81 *1 from equation (3) & (4)

:. 0.5 VD = 9.81 usin/ucos = 29.43/17.069

:. VD = 19.62 m/s : tan = 1.724

:. = 59.886& u = 29.43/sin54.886 =34.02 m/s

Q4) A projectile is fired from the edge of 150 m cliff an initial velocity of 180 m/s at 30

angle with Horizontal. Find 1) The Horizontal distance from the gun to the point where the projectile strikes the ground 2) The greatest elevation above the ground reached by projectile 3) striking velocity. Refer the given figure.

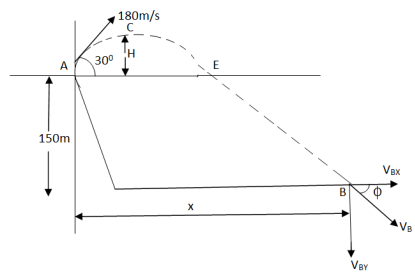
$C:\Users\Ssd\Desktop\unit 1 2.png$

A4)

Let

X= Horizontal distance between A& B

A= point of projection

B= point of striking.

We can see from the fig that A& B are not on same level. TAB = time Req = tAB

Consider the Horizontal motion from A to B (U.M)

:. Distance = velocity * time

X = 180 cos 30 * tAB

X= 155.88 tAB ------ (1)

Consider vertical motion from A to C, H+ 150+ ½*9.81* t2CB

: V = u + at 412.84+ 150 = 4.905 +tCB

Vcy = 180sin30- g*tAC : t2CB = 562.84/4.905

:0 = 90 – 9.81 tAC :. t2CB = 114.748

:tAC = 90/9.81 :. tCB = 10.71 sec

:tAC = 9.17 sec. tAB = 9.17 + 10.71 = 19.88 sec
Consider vertical motion from A to E from eqn (1)

H = u2sinsin2 /2g = 1802*sin2 30/2*9.81 X = 155.88 tAB = 155.88*19.88

X = 3098.9 m

H = 412.84 m.

:. Now using Equation of motion

S = ut + ½ gt2

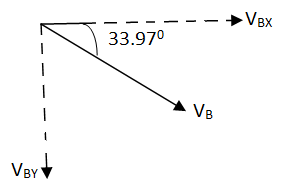
Horizontal distance from the to the point of striking is

X = 3098.9 m

Time req. from A to B = tAB = 19.88 sec.

Greatest Height Reached by projectile above the ground is

Hmax H + 150 = 412.84+150

Hmax = 562.84 m

Now,

Consider that VB = striking velocity. &

Ø = angle made by striking velocity with Horizontal. As shown.

Let VBX = X component of VB.

VBy = y component of VB.

But we know that, in X dirn, motion is uniform.

Thus VBX = u cos = 180 cos 30 = 155.88 m/sec.

To find VBy consider the motion from C to B.

:. V = u + gt

VBy= Vcy + g * tCB

VBy = 0 + 9.81 * 10.71

VBy = 105.06 m/sec

$C:\Users\Ssd\Desktop\UNIT 1 3.png$

:. VB = VBX2 +V2BY = 155.882 + 105.062

VB = 187.9 m/sec

Tanø = VBy/ VBX = 105.06/155.88

:. Ø = 33.97

Key points

1) Time of flight (t)

t 2 u sin/

2) Horizontal Range (R)

R = u2. Sin2/

3) Maximum Range (R max)

For maximum Range angle of projection must be 45

R max = u2/

4) Maximum Height

H = u2. Sin2/2

Q5) The acceleration versus time for a particle moving along x axis is given in the figure given below. The time interval is 0 to 40 sec for some time interval plot 1) V-t diagram(2) x – t diagram(3) also find max speed attained & max distance covered Diagram

$C:\Users\Ssd\Desktop\unit 1 4.png$

A5)

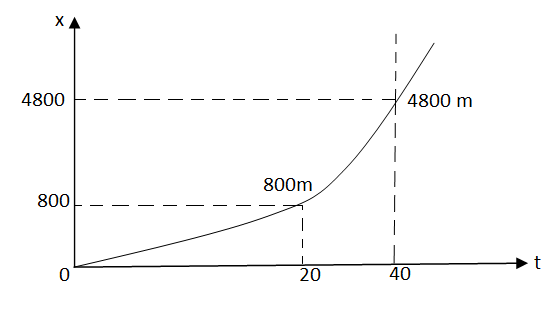
We know that,

Change in velocity= area under a-t diagram from the given a – t diagram

∴at T =20sec

V20 - v0 = 1/2 x 20x12

V20- v0 =120 m/sec

But at T=0 v0= 0

∴ 20= 120m/sec

Now,

At t =40 sec

∴ v40- v20= ½x 20 x12 = 120

∴ v40 = 120+v20

∴ v40 = 240m/sec

Thus v -t diagram will be as follows

$C:\Users\Ssd\Desktop\unit 1 5.png$

Now from above v -t diagram

Change in displacement = area under v-t diagram

At t=20sec

X20 -X 0 =1/3 x 20x 120 =800m

As (X0 = 0 at t = 0)

∴X20 = 800m

At t =40sec

X40 - X20 = (20x 120) + (2/3 x20 x120)

X40 = 2400+1600+ X20

X40 = 24001600+800

X 40= 4800m

∴ x -t diagram will be as follows

$C:\Users\Ssd\Desktop\unit 1 6.png$

Max speed attained = 240m/sec

Max distance travelled = 4800m

Q6) Write special cases of motionA6)

SPECIAL CASES OF MOTION

There are some special cases of motion to consider.

1) The particle moves along a curve at constant speed.

at = v = 0

=a = an = v2 /ρ.

The normal component represents the time rate of change in the direction of the velocity.

2) The particle moves along a straight line.

ρ- => an = v2 /ρ = 0 => a = at = v

The tangential component represents the time rate of change in the magnitude of the velocity.

3) The tangential component of acceleration is constant,

at = (at )c .

In this case,

As before, so and vo are the initial position and velocity of the particle at t = 0

4) The particle moves along a path expressed as y = f(x). The radius of curvature, r, at any point on the path can be calculated from

Q7) Explain three-dimensional motionA7)

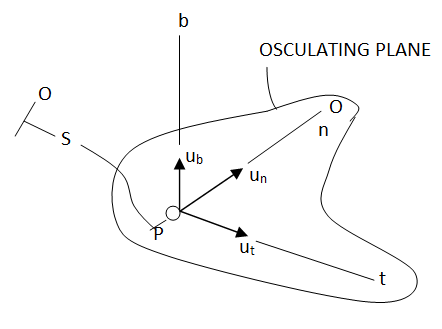
THREE-DIMENSIONAL MOTION

If a particle moves along a space curve, the n and t axes are defined as before.

$C:\Users\Ssd\Desktop\UNIT 1 7.png$

At any point, the t-axis is tangent to the path and the n-axis points toward the center of curvature. The plane containing the n and t axes is called the osculating plane. A third axis can be defined, called the binomial axis, b. The binomial unit vector, ub, is directed perpendicular to the osculating plane, and its sense is defined by the cross product ub = ut x un There is no motion, thus no velocity or acceleration, in the binomial direction.

Q8) Explain Kinematics?A8) Kinematics is the branch of mechanics or simply a part of dynamic analysis which deals with the study or analysis of the motion of the body without considering the forces that causes this motion.Hence Kinematics only analyses the geometry of the particle or rigid body. Q9) Explain Kinetics?A9) Kinetics is the branch of mechanics or simply a part of dynamic analysis which deals with the study of motion of the body by considering the forces that causes this motion.In other words, kinematics relates with the forces acting on the moving body. Q10) Write classification of dynamics?A10) Dynamics can be also classified on the basis of the body under study.

Particle dynamics

Particle is nothing but a point body or a body who does not have any size and shape. Analysis of a particle in motion is referred to as particle dynamics2. Rigid body dynamicsRigid body is a body that does not change its shape and size when subjected to various forces and couples. Analysis of rigid body is referred to as rigid body dynamics

Sign Up