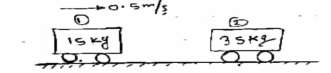Q3 Explain dynamics | unit 5 collision of elastic bodies

Back to Study material

UNIT - 5Collision of elastic bodiesQ1) A 75 kg man stands on a spring scale in an elevator. During the first 3 seconds of motion from rest, the tension Tin the hoisting cable is 8300 N. Find the reading R of the scale in Newton during this interval and the upward velocity v of the elevator at the end of the 3 seconds. Total mass of elevator, man, and scale is 750 kg.A1)

Draw the FBD of the elevator and the man alone

During first 3 seconds, the forces acting on the elevator are constant. Therefore, the acceleration ay will also remain constant during this time.

Force registered by the scale and the velocity of the elevator depend on the acceleration ay From FBD of the elevator, scale, and man taken together:

ΣFy= may =8300-7360 =940 (m=750)

750ay = 940

ay= 940/750 = 1.257 m/s2

From FBD of the man alone:

ΣFy= may = R-736 = 75ay

R= 830 N

Velocity reached at the end of the 3 sec:

v= 3.77 m/s

Q2) Find the differences between static and dynamic equilibrium?A2)

Static vs Dynamic Equilibrium
Dynamic Equilibrium	Static Equilibrium
This type of equilibrium is reversible in nature.	This type of equilibrium is irreversible in nature.
This equilibrium implies that the reactants and the products are still participating in chemical reactions.	There is no further chemical reaction in the system.
In dynamic equilibrium, the forward and the backward reaction rates are equal	In static equilibrium, the forward and backward reaction rates are zero
It can only occur in closed systems	It can occur in both open and closed systems

Q3) Explain dynamicsA3)Dynamics is the branch of mechanics that deals with the motion of the particle or a rigid body. In other words, dynamics deals with the accelerated motion of a body. Analysis in dynamics involves motion. Dynamics can be sub-divided into two parts:

Kinematics

Kinematics is the branch of mechanics or simply a part of dynamic analysis which deals with the study or analysis of the motion of the body without considering the forces that causes this motion.Hence Kinematics only analyses the geometry of the particle or rigid body.2. KineticsKinetics is the branch of mechanics or simply a part of dynamic analysis which deals with the study of motion of the body by considering the forces that causes this motion.In other words, kinematics relates with the forces acting on the moving body. Dynamics can be also classified on the basis of the body under study.

Particle dynamics

Particle is nothing but a point body or a body who does not have any size and shape. Analysis of a particle in motion is referred to as particle dynamics2. Rigid body dynamicsRigid body is a body who does not change its shape and size when subjected to various forces and couples. Analysis of rigid body is referred to as rigid body dynamics

Q4) Two masses of 15 kg & 20 kg are moving along a straight line towards each other at velocities of 4 m/a & 2 m/s respectively . If e = 0.6, find the velocities of the masses immediately after the collision. Also find %in K.E. due to impact.A4)

Description: IMG-20191220-WA0024.jpg

Let V1 &V2 are the velocities after collision, assume that both are towards right ( )

Using law of conservation of momentum,

(15

20 = 15V1+20V2 ___________1

Using coefficient of restitution

e =

0.6 =

V2-V1= 0.66

V 2 – V 1 = 3.6

-V 1 + V2= 3.6 ______________2

Solving 1 & 2

15 V1 + 20 V2 = 20

-V1 + V2 = 3.6

We get V2= 2.11 m/s ( )

& V1 = - 1.43 m/s ( )

Loss in KE = initial KE- final KE

Loss of K.E. = -

= (½

= (120+40) – (16.65+44.52)

= 160 - 60.97

Loss in K.E = 99.029 joule.

% Loss in K.E = 99.029/160

= 61.89%

Q5) The perfectly elastic balls 1, 2, 3 of masses 2kg 6kg 12kg respectively move along a line in same direction with velocities 12 m/s 4m/s and 2 m/s respectively. If the ball 1 strikes the ball 2 which in horn strike ball 3 determine velocity of each ball after impact.

Description: IMG-20191220-WA0025.jpg

A5)

Given data

Ball 1

M1 = 2kg u1 = 12 m/s

Ball = 2

M2 = 6kg u = 4 m/s

Ball = 3

M3 = 12 kg u = 2 m/s

Consider the impact between ball 1 and ball2

For law of conversation of momentum

M1u1 + m2u2 = m1 v1 + m2v2

2*12 + 6*4 = 2v1 +6v2

48= 2v1 +6v2

2v1 + 6v2 = 48 - - - - - - - - - - -- -equation 1

As the balls are perfectly elastic

E= = 1

V2 – v1 = u2 – u1 = 12 -4 = 8

V2 – v1 = 8 - - - - - - - - - - - - - - - - - -equation 2

Solving equation 1 and 2

V1 = 0 and v2 = 8 m/s

As the ball strike each other ball 1 comes to rest and ball 2 moves forward ball s with new velocity of 8 m/s

U2 = 8 m/s

B) consider the impact between the ball 2 and 3

M2 u2 + m3 u3 = m2v2 + m3v3

6* 8 + 12*2 = 6V2 + 12v3

6V2 + 12 v3 = 72 ---------------- equation 3

perfectly elastic balls

e = 1 = =

-V2 + v3 = 6 ------------------------ equation 4

Solving equation 3 and 4 we get

V2 = 0 and v3 =6 m/s

Q6) Two smooth balls A & B having mass of 4 kg and 8 kg respectively collider with initial velocities as shown in figure .if coefficient of restitution is e = 0.8 , find the velocities of each ball after the collision.

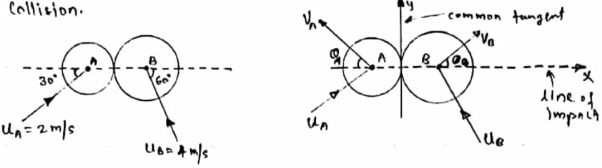
Description: IMG-20191220-WA0026.jpg

A6)

Ball – A

Using law of conservation of momentum along direction

(4) + ( 8

6.928 + (-16) = -

- = -9.072 - - - - - - - -----1

Coefficient of restitution,

e = 0.8

0.8 = VB X + VA X /

VB X + VA X= 2.986 ---------------------2

Solving 1 & 2 we get

VB X = 0.239 m/s

VA X= 2.746 m/s

Similarly, now component of velocity before and after the impact is conserved i.e. remain constant along the common tangent

V AY = UAY = = 1 m/s

V BY= U B Y =4 = 3.46 m/s

= = 2.92 m/s

== 3.468 m/s

=20

= 086.05

Q7) A 20 gm. bullet horizontally into 300 gm. block, which rest on smooth surface. After impact the bullet percentage into black the block moves to the right through 300 mm before momentarily coming to rest .determine speed of bullet as it strike the block the block is resting on smooth surface against the spring which is originally unstreched & has a constant of 200 n/m

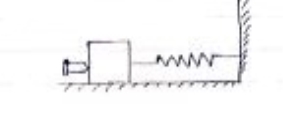
Description: Capture.JPG

A7)

Given data

For bullet

M1 =0.02kg, u=?

For block,

m2 = 0.3 kg, u2 = 0

As the bullet penetrates into the block after the impact

The impact is perfectly plastic.

After impact velocity of block & bullet will be equal

V = V2 = V1 = common velocity

By applying law of conservation of momentum, for impact

0.02 u 1 +0.3

0.02 u 1 = (m1 + m2) v

0.02 u 1 = (0.02 + 0.3) v

0.02U 1 = 0.32 v

As the impact takes place, the black along with bullet will move toward right against spring force before coming to rest here spring will be compressed by 300 mm

Applying work energy principal just after the impact,

Total work done= kinetic energy 2 – kinetic energy 1

Work done by spring force = KE 2 – KE 1

½ (0.02+0.3) ]

-9= - 0.16

V = 7.5 m/s - ------ put this is in equation 1

0.02 u 1 = 0.32 v1 = 0.327.5

U 1 = 120 m/s - - - - -speed of the bullet as it strikes the block

Q8) A 100 gm ball dropped from a height of 600 mm on a small plate .it rebounds to a height of 400 mm when plate is directly resting on ground floor and it rebounded to a height of 250 mm when foam rubber matt is placed between plate and ground determine the coefficient of restitution between the plate and ground. A8) Case 1

= 600 mm

= 400 mm e =

e =

e = 0.816 Case 2

= 600 mm

= 250 mm e =

e = 0.645. Q9) A body starts from rest and is acted on by a constant force. What is the ratio of kinetic energy gained by it in the first five seconds to that gained in the next five second?A9)

1) constant force → constant acceleration =a
=V5−v0 / t = a

=V5−0/ 5=a

=V5=5a
⇒K.E5=mV2=25/2 ma2

2) v10−v0/t =a

⇒v10=10a

⇒K.E10=100/2 ma2
So K.E gained between 5s and 10s =K.E10−K.E5
=75/2 ma2
K.E gained in 5s=25/2 ma2
= Ratio =25/75 =1:3

Q10) Shish is going by a slippery snowy hill. He has a mass of 20kg, and he is sliding the hill at a velocity of 5m/s. Shish’s elder brother has a mass of 30kg. His brother is moving slower with a velocity of 2m/s. Shish collides to his brother. Then both of them keep going down the hill as one unit. Calculate the resulting velocity of Shish?A10)

Given,

M1= 20kg

M2= 30kg

V1= 5m/s

V2= 2m/s

We know that When two objects collide under inelastic condition. The final velocity with which object move is given by-

V = (M1V1+M2V2)/ (M1+M2)

V= (20kg) × (5m/s) + (30kg) × (2m/s) / (20kg+30kg)

= (100kg.m/s+60kg.m/s) / 50kg

= (160kg.m/s) / 50kg

=3.20m/s

Sign Up