UNIT 1

UNIT 1

Question 1-: Evaluate

Solution:

Let

…

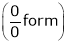
By L – Hospital rule,

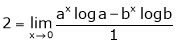
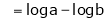
Question-2: Evaluate

Solution:

Let

…

By L – Hospital rule

…

…

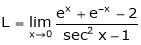Question-3: Find the value of a, b if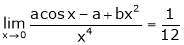

Solution:

Let

…

By L – Hospital rule

…

…

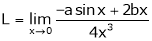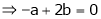… (1)

…

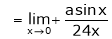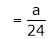
But

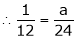
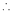From equation (1)

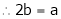
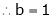
Question-4: Evaluate

Solution:

Let

…

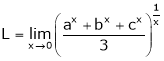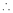Taking log on both sides,

…

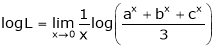
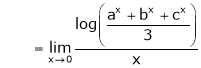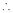By L – Hospital rule,

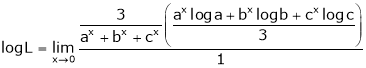
i.e.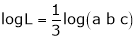

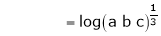
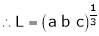
Question-5: find out the integral 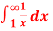is convergent or divergent. Find the value in case of convergent.

Sol.  Here we will convert the integral into limit ,

                                              =

                                                               =

                                                               =

                                                              = ∞

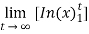
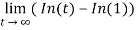
As we can see , here limit does not exist. i.e. that is infinity.

So we can say that the given integral is divergent.

Question-6: find out the integral is convergent or divergent. Find the value in case of convergent.

Sol. Covert to the limit ,

                                          =

                                                              =

                                                              =

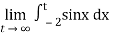
Again the limit does not exist that means the integral is divergent

Question-7: find out the integral 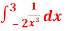is convergent or divergent. Find the value in case of convergent.

Sol.  As we see, the given is integrand is not continuous at x = 0 , we will split the integral,

                              =   +      

We will check one by one whether the integrals are convergent or divergent,

As we found that, integral is divergent

We don’t need to check for the second one.

Question-8: Find  γ(-½) 

Solution:       (-½) + 1  =  ½
γ(-1/2)  =   γ(-½ + 1)  / (-½)   

=   - 2   γ(1/2 )  

=  - 2 π  

Question-9: .  Show that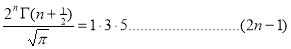    

Solution : =

                                          =

                                          = )  .......................

                                          =

                                          =

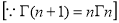
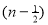
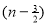
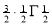
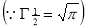
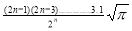
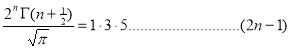
Question-10: ):  Evaluate    I   =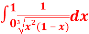  

Solution:

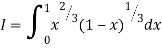
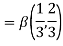
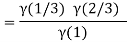
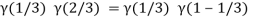
                          = 2 π/3

Question-11:  Evaluate

Solution :Let

Put   or  ,,

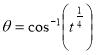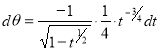
When,;,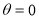

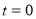
	o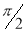
	1	0

Also

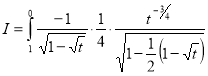
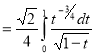
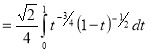
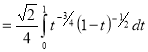
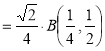
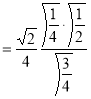
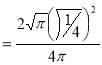
Question- 12: find the area under the curves where y =  x and y =  x + 1,         x = 2 and y-axis.

Sol. When we draw the graph, curve does not meet, but depend on two vertical lines,

Here boundary is [0 , 2]

Area under the curve,

                                              A =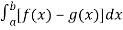

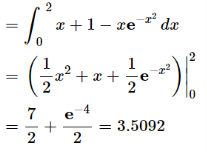
So that the area under the curve is 3.2092 unit square.

Question-13: find the average value of the function f(x) = x³ over the interval[0,1].

Sol.  We know that

                                 f( avg.) =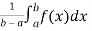      

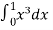                                              =      =       = 1 / 4

Question-14: A force of 1200 N compresses a spring from its natural length of 18 cm to a length of 16 cm. How much work is done in compressing it from 16 cm to 14 cm?

Sol.  Here,

                          F = kx

So that,

                         1200 = 2k

                             K = 600 N/cm

In that case,

                                 F = 600x

We know that,

                               W =      

                               W =       , which gives

                    W  = 3600 N.cm

Question-15: Find the volume of the solid of revolution generated by rotating the region between the graph of f(x) = √x over the interval [1,4] around x-axis.

Sol. The graph of the function will look like as follow,

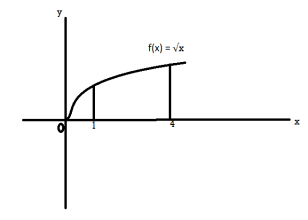
On rotation it will make circle ( cross-section)

We know that,

                             V =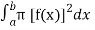       

                                =     =    , which gives

                               = 

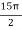
The volume is

Question-16: suppose a wire hanging on two poles follows the curve,

                                      f(x) = a cosh(x/a)

Find the length of the wire.

Sol. We will find the first derivative of f(x),

                                          f’(x) =  sinh(x/a)

The curve of f(x) will look like,

Hence the curve os symmetric, we will measure the length of one side first,

The limits on one side will be, 0 to b

We know that

                              Length of Arc  = 

Put  f’(x) =  sinh(x/a), we get

                            Length of Arc  =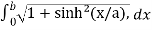 

Use the identity,

                                                       =

                                                       =

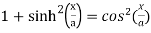
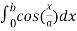
We get on solving,

                                              a sinh(b/a)

On both sides, the length of the curve will be,

                                              2 a sinh(b/a)