Unit 1

1. Explain the electrical circuit elements?

The three essential elements in circuit analysis:

• Resistance R

• Capacitance C

• Inductance L

Their V and I relationships are summarized below

Resistance is a static element in the sense v(t) versus i(t) relationship is instantaneous. For example, v(t) at time t = 2 seconds simply depends only on i(t) at t = 2 seconds and nothing else. This implies that the resistance does not know what happened in the past, in other words it does not store any energy unlike other elements C and L.

Capacitance: Time domain:

q(t) = Cv(t)

 i(t) = dq /dt = C dv/ dt

Dv/dt = 1/C i(t)

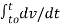= v(t) – v(to) = 1/C  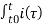 d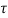

For a capacitance the v(t) versus i(t) relationship and vice versa at any time t depends on the past as they involve differentials and integrals. This implies that the capacitance is a dynamic element.

Inductance:

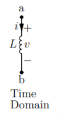
Time domain v(t) = L di/dt

Di/dt = 1/L v(t)

        = i(t) – i(to) = 1/L     d τ

i(t) = i(to) + 1/L 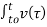  dτ

2.     Explain the voltage and current sources?

Ideal and practical Voltage and Current source:

A voltage source is a device which provides a constant voltage to load at any instance of time and is independent of the current drawn from it. This type of source is known as an ideal voltage source. Practically, the ideal voltage source cannot be made. It has zero internal resistance. It is denoted by this symbol.

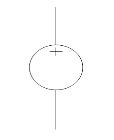
            Fig:  Voltage source symbol

Ideal Voltage Source

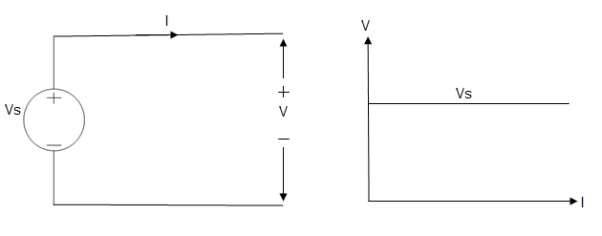
                                          Fig: Ideal Voltage Source

The graph represents the change in voltage of the voltage source with respect to time. It is constant at any instance of time.

Voltage sources that have some amount of internal resistance are known as a practical voltage source. Due to this internal resistance, voltage drop takes place. If the internal resistance is high, less voltage will be provided to load and if the internal resistance is less, the voltage source will be closer to an ideal voltage source. A practical voltage source is thus denoted by a resistance in series which represents the internal resistance of source.

Practical Voltage source

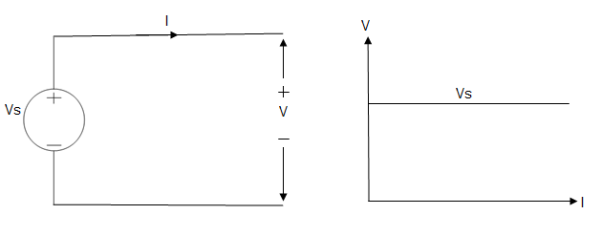
                                      Fig: Practical Voltage source

The graph represents the voltage of the voltage source with respect to time. It is not constant but it keeps on decreasing as the time passes.

Current source

A current source is a device which provides the constant current to load at any time and is independent of the voltage supplied to the circuit. This type of current is known as an ideal current source; practically ideal current source is also not available. It has infinite resistance. It is denoted by this symbol.

Ideal Current source

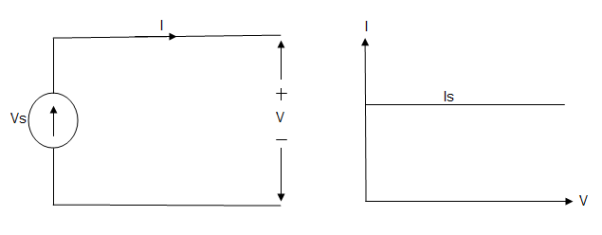
                                                          Fig: Ideal Current source

The graph represents the change in current of the current source with respect to time. It is constant at any instance of time.

Why ideal Current source has infinite resistance?

A current source is used to power a load, so that load will turn on. We try to supply 100% of the power to load. For that, we connect some resistance to transfer 100% of power to load because the current always takes the path of least resistance. So, in order for current to go to the path of least resistance, we must connect resistance higher than load. This is why we have the ideal current source to have infinite internal resistance. This infinite resistance will not affect voltage sources in the circuit.

Practical Current source

Practically current sources do not have infinite resistance across there but they have a finite internal resistance. So the current delivered by the practical current source is not constant and it is also dependent somewhat on the voltage across it.

A practical current source is represented as an ideal current source connected with resistance in parallel.

                                                Fig; Practical Current source

The graph represents the current of the current source with respect to time. It is not constant but it also keeps on decreasing as the time passes.

3.     Explain Kirchhoff’s current and voltage law?

The algebraic sum of currents meeting at a junction or node in a electric circuit is zero ② or the summation of all incoming current is always equal to summation of all outgoing current in an electrical network.

Explanation

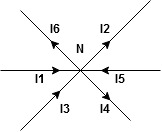
Assuming the incoming current to be positive and outgoing current negative we have

Ie incoming current = ∑ outgoing current thus, the above Law can also be stated as the sum of current flowing towards any junction in an electric circuit is equal to the sum of currents flowing away from that junction

Kirchhoff’s Voltage Law (KVL)

Statement : the algebraic summation of all Voltage in any closed circuit or mesh of loop zero.

Ie  ∑ Voltage in closed loop = 0 the summation of the Voltage rise (voltage sources) is equal to summation of the voltage drops around a closed loop in 0 circuit for explanation from here

Determination of sigh and direction of currents (Don’t write in exams just for understanding)

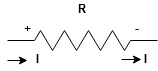
Current entering a resistor is +ve and leaving should be –ve

Now

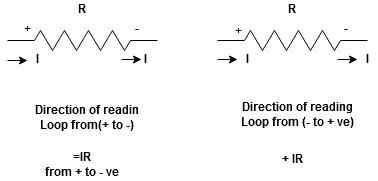
Potential RisePotential Drop

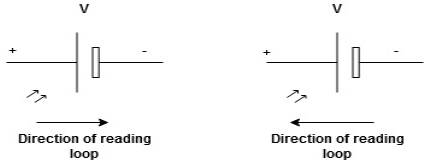
We are reading from +V to –Vwe are reading from –V to +V

potential drops potential rise

-V +V

4.     Resistors of R1= 10Ω, R2 = 4Ω and  R3 = 8Ω are connected up to two batteries (of negligible resistance) as shown. Find the current through each resistor.

Assume currents to flow in directions indicated by arrows.
Apply KCL on Junctions C and A.
Therefore, current in mesh ABC = i1
Current in Mesh CA = i2
Then current in Mesh CDA = i1 – i2

Now, Apply KVL on Mesh ABC, 20V are acting in clockwise direction. Equating the sum of IR products, we get;
10i1 + 4i2 = 20 ……………. (1)

In mesh ACD, 12 volts are acting in clockwise direction, then:
8(i1–i2) – 4i2= 12

8i1 – 8i2 – 4i2= 12
8i1 – 12i2 = 12 ……………. (2)

Multiplying equation (1) by 3;
30i1 + 12i2 = 60

Solving for i1
30i1 + 12i2 = 60
8i1 – 12i2 = 12

______________
38i1 = 72

The above equation can be also simplified by Elimination or Cramer’s Rule.

i1 = 72/38 = 1.895 Amperes = Current in 10 Ohms resistor

Substituting this value in (1), we get:
10(1.895) + 4i2 = 20

4i2 = 20 – 18.95

i2 = 0.263 Amperes = Current in 4 Ohms Resistors.

Now,
i1 – i2 = 1.895 – 0.263 = 1.632 Amperes

5.     Explain the analysis of DC circuit with excitation?

Here is a simple circuit with DC excitation:

Analysis would mean we determine the voltages at all the nodes and currents in all the branches of this circuit.

A node is defined as any point where two or more components meet.

A branch is defined as any path between two nodes.

Let’s label all the nodes in the circuit above:

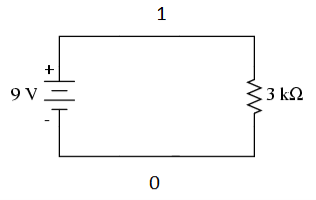
We have only two nodes here, ‘1’ and ‘0’.

We call node ‘0’ the ground node. The ground node is at 0 volt.

Node ‘1’ is connected to the top of our DC voltage source. So it is at 9 volts.

Half our job is done here, because we now know the voltages at all the nodes in our circuit.

Next, let’s talk about the branches.

There are two branches in our circuit. One branch contains the 9V DC source and the other branch contains the 3k resistor.

We know find the currents through the branches.

From Ohm’s law we can calculate the current in the resistor.

I = V/R

This gives us a current of 9/3k = 3 mA.

The current in the resistor branch is 3 mA. And, because our circuit is one single closed loop, this current also flows in the other branch.

At this point, we know all the voltages at each node and the currents through each branch of our simple circuit. So, we say that the analysis of our simple DC excitation circuit is complete.

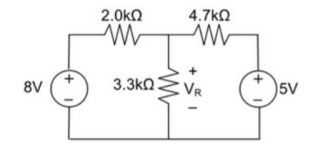
Step 1:

Remove 8V power supply from the original circuit such that the new circuit becomes as the following and measure the voltage across resistor.

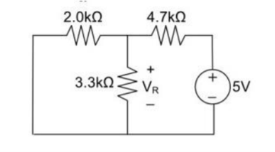
Here 3.3 K and 2K are in parallel therefore the resultant resistance will be 1.245K

Using voltage divider rule across 1.245K will be

V1 =[1.245/(1.245+4.7)] * 5 = 1.047V

Step 2:

Remove the 5V power supply from the original circuit such that the new circuit becomes the following and then measure the voltage across resistor.

Here 3.3K and 4.7K are in parallel therefore the resultant resistance will be 1.938K. Using voltage divider rule voltage across 1.938K will be

V2 =[1.938(1.938+2)] *8 = 3.9377V

Therefore, voltage drop across 3.3K resistor is V1+V2 = 1.047 + 3.9377 = 4.9847V

7.For the circuit as shown in figure find the current through RL = R2 = 1Ω resistor (Ia-b) branch using Thevenin’s theorem. Find the voltage across the current source.

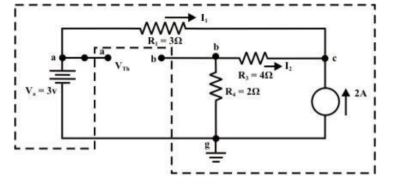
Step 1: Disconnect the load resistance and reconnect the circuit.

Step 2: Apply any method to calculate Vth

At node C

2 + I1 + I2 =0

2 + (3 -Vc)/3 + (0-Vc/6) -- Vc = 6V

The currents I1 and I2 are computed by the following expressions:

I1 = Va -Vc/3 = 3-6/3 = -1A (I1 is flowing from c to a)

I2 = 0 – Vc/6  = -6/6 = -1A (I2 is flowing from c to a)

Step-3:

Redraw the circuit indicating the direction of currents in different branches. One can find the Thevenin’s voltage VTh using KVL around the closed path ‘gabg’

VTh = Vag − Vbg = 3 − 2 =1volt

Step 4:

Replace all sources by their internal resistances. In this problem, voltage source has an internal resistance zero (0) (ideal voltage source) and it is short-circuited with a wire.

On the other hand, the current source has an infinite internal resistance (ideal current source) and it is open-circuited (just remove the current source).

Thevenin’s resistance RTh of the fixed part of the circuit can be computed by looking at the load terminals ‘a’- ‘b’

RTh = ( R1 + R3 ) & R4 = ( 3 + 4 )&2 = 1.555Ω

Step-5: Place RTh in series with VTh to form the Thevenin’s equivalent circuit. Reconnect the original load resistance RL = R2 = 1 Ω to the Thevenin’s equivalent circuit .

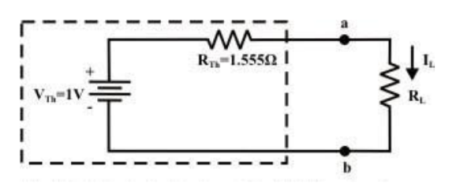
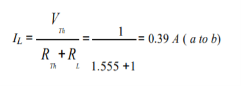
Step-6: The circuit is redrawn to indicate different branch currents. Referring to one can calculate the voltage Vbg and voltage across the current source (Vcg ) using the following equations.

Vbg = Vag − Vab = 3 − 1 × 0.39 =2.61 volt.

Ibg = 2.61 2 = 1.305 A;

Icb = 1.305 − 0.39 = 0.915 A

Vcg = 4 × 0.915 + 2 ×1.305 =6.27 volt.

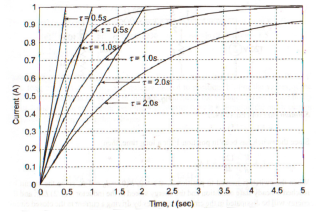
8.Explain the time domain analysis for R-L circuit?

Above equation is non homogeneous equation linear differential equation of first oder. The solution of equation 1 will give i(t) which consists of two components :

Complimentary function

Which will satisfy di(t)/dt + R/L i(t) =0

Particular integral (if(t)) which will satisfy

R i(t)  + L di(t)/dt = Vs

Thus the complete solution wil be

i(t) = in(t) + iJ(t)---------------------------------------(2)

i(t) = Io e –(R/L)t = Io e –(t/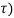-------------------------------------(3)

Where 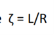   time constant of RL circuit.

Equation (3) provides the natural response where

in(t)  = K e –(R/L) t = K e –(t/τ) ----------------------------------(4)

Eq (1) can be written with i(t) = I constnt

RI + L dI/dt = Vs -------------------------------------------(5)

Since I= constsnt

L dI/dt =0

If(t) = I = Vs/R --------------------------------------------(6)

Substitute eq.4 and eq.6 yeilds the solution of eq(1)

i(t) = K e -t/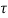 + Vs/R = K e-t/τ    -------------------------------------------(7)

K is determined from initial condition that is t=0 and eq(7) will be

K = -Vs/R = -I ----------------------------------------------------(8)

i(t) = Vs/R (1 – e –(R/L) t)

i(t) = I(1 – e -t/τ)                                                  for t>0

9. Explain the time domain analysis of RC circuit?

Series RC circuit:

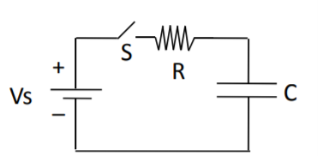
Fig. Shows a series RC circuit connected across a DC source through a switch S.

It is assumed that capacitor voltage id V0 When switch ‘S’ is close at t>0 the as per KVL network

Equation will be …

Vs – R i(t) – vc(t) =0 ------------------------------------------------(9)

For analysis of circuit of the figure the capacitor voltage Vc(t) is chosen as variable .

Substituting i(t) = c dvc(t)/dt in eq(9) we get

Eq(10) is like eq(1) it is also non homogeneous equation linear differential equation

Of first order .

Therefore the solution is similar to eq(1)

Vc(t) = k e -t/τ + Vs ---------------------------------------------(11)

In eq.(11) the time constant is τ = RC

By substituting value of K in eq(11) and after simplification we get --------

Vc(t) = Vo e (-t/τ) + Vs ( 1 – e -t/τ) V      for t>0------------------------------------------(12)

The expression for the current in the circuit is given by ---------

i(t) = C dvc(t)/ dt

i(t) = C [ (-1/τ Vo e -t/τ  ) + ((-1/τ Vs e -1/τ  )]

i(t) = C/RC (Vs – Vo) e -t/τ 

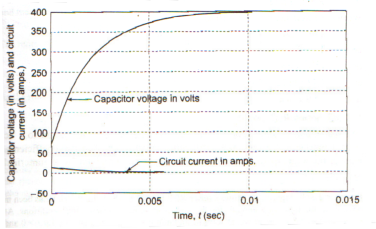
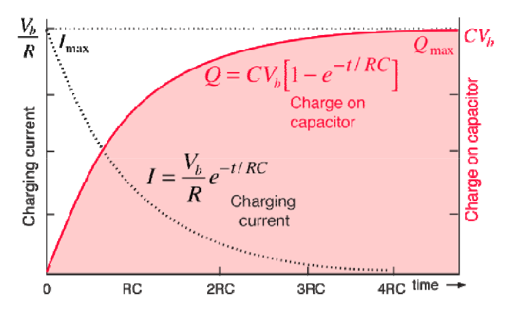
10. What are the applications of RL and RC circuits?

RC and RL circuits are nothing more than applications for resistors, inductors, and capacitors.  RC circuits since they are more commonly used and especially they're widely used with computers circuits and digital circuits .