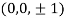Question Bank ( unit – 4 GTU)
Question Bank ( unit – 4 GTU)
Question-1: evaluate the
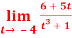
Sol. We can simply find the solution as follows,

Example-2: evaluate 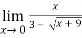
Sol.
 -6.
-6.
Question-2: Test the continuity of the following function-

Sol. (1) the function is well defined at (0,0)
(2) check for the second step,
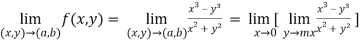
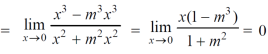
That means the limit exists at (0,0)
Now check step-3:
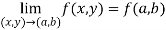
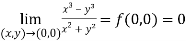
So that the function is continuous at origin.
Question-3: Evaluate 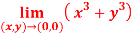
Sol . 1. 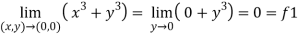
2. 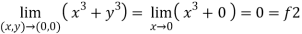
Here f1 = f2
3. Now put y = mx, we get
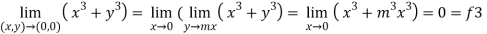
Here f1 = f2 = f3
Now put y = mx²
4. 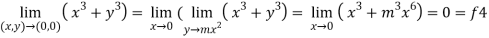
Therefore ,
F1 = f2 = f3 =f4
We can say that the limit exists with 0.
Question-4: evaluate the following-
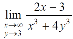
Sol. First we will calculate f1 –
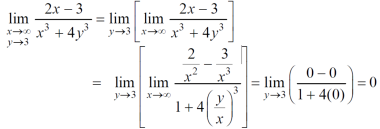
Here we see that f1 = 0
Now find f2,
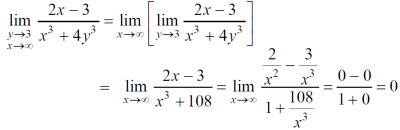
Here , f1 = f2
Therefore the limit exists with value 0.
Question-5: Calculate 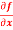 and
and 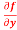 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate 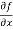 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
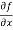 =
= 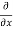 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] - 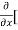 5y²] +
5y²] +  [2xy] -
[2xy] -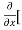 8x] +
8x] +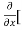 4y] -
4y] - 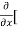 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
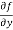 =
= 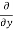 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] - 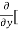 5y²] +
5y²] + 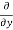 [2xy] -
[2xy] -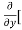 8x] +
8x] +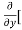 4y] -
4y] - 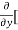 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Question-6: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Sol. 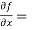 3x²y² - y⁵,
3x²y² - y⁵,  2x³y – 5xy⁴,
2x³y – 5xy⁴,
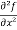 =
= 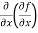 = 6xy²
= 6xy²
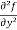 =
= 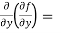 2x³ - 20xy³
2x³ - 20xy³
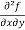 =
= 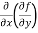 = 6x²y – 5y⁴
= 6x²y – 5y⁴
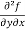 =
= 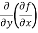 = 6x²y - 5y⁴
= 6x²y - 5y⁴
Question-7: : if,
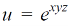
Then find.
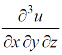
Sol-
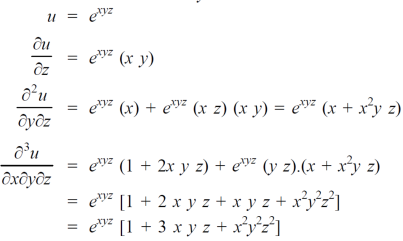
Question-8: verify mixed derivative theorem for
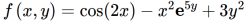
Sol. We will find first derivatives,

Then we find second derivative ,
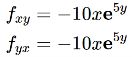
We see that,
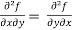 verified.
verified.
Question-9: suppose that the function,
f(z) = 4x + y + i( -x + 4y)
Discuss df/dz.
Sol. Here,
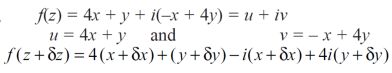
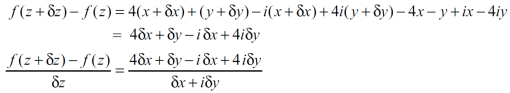
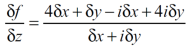
Question-10: If w = x² + y – z + sin t and x + y = t then find

Sol. With x, y and z independent , we have
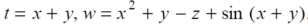
Therefore , we get
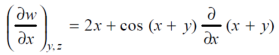
= 2x + cos ( x+ y)
Question-11: determine the gradient of the function ,
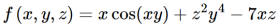
Sol. We know that, the gradient for three vairables,
grad f = 
So that, we get the gradient as below,
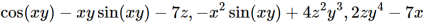
Question-12: let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find 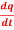 .
.
Sol. : 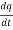 . =
. = 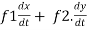
Where, f1 = 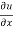 , f2 =
, f2 = 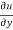
In this example f1 = 4 , f2 = 3
Also, 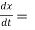 3t² + 2t ,
3t² + 2t , 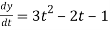
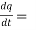 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(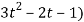
= 21t² + 2t – 3
Example-2: Find 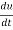 if u = x³y⁴ where x = t³ and y = t².
if u = x³y⁴ where x = t³ and y = t².
Sol. As we know that by definition, 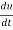 =
= 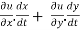
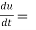 3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
Question-13: if w = x² + y – z + sint and x + y = t, find
(a) 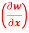 y,z
y,z
(b) 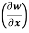 t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x² + y - z + sin (x + y).
Therefore,
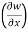 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)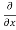 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
thus 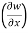 t, z = 2x - 1
t, z = 2x - 1
Question-14:Find the points on the surface 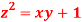 nearest to the origin.
nearest to the origin.
Sol.
Let 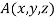 be any point on the surface, then its distance from the origin
be any point on the surface, then its distance from the origin  is
is
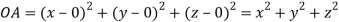
Thus the given equation will be
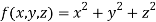
And relation is 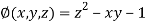
By Lagrange’s Method

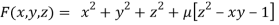 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
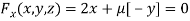
Or 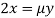 …(ii)
…(ii)
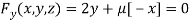
Or 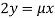 …(iii)
…(iii)

Or 
Or 
On solving equation (ii) by (iii) we get
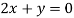
And 
On subtracting we get 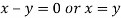
Putting in above 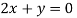
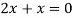
Or 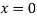
Thus 
Using the given relation we get
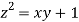 = 0.0 +1=1
= 0.0 +1=1
Or 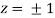
Thus point on the surface nearest to the origin is