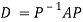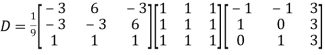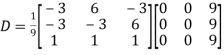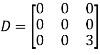Question Bank (unit-6)
Question-1: : Prove that the following matrix is orthogonal:
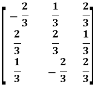
Let A =  then A’=
then A’= 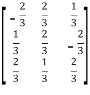
Now, AA’=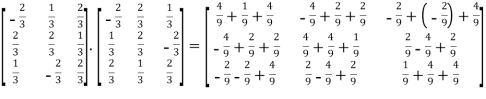
Thus AA’=  = I
= I
Hence the matrix is orthogonal.
Question-2: Find the rank of a matrix M by echelon form.
M = 
Sol. First we will convert the matrix M into echelon form,
M = 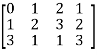
Apply, 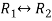 , we get
, we get
M = 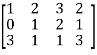
Apply  , we get
, we get
M = 
Apply 
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Question-3: Find the rank of a matrix A by echelon form.
A = 
Sol. Convert the matrix A into echelon form,
A = 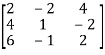
Apply 
A = 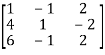
Apply 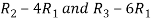 , we get
, we get
A = 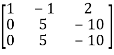
Apply 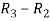 , we get
, we get
A = 
Apply 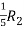 ,
,
A = 
Apply  ,
,
A = 
Therefore the rank of the matrix will be 2.
Question-4: Find the rank of a matrix A by echelon form.
A = 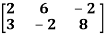
Sol. Transform the matrix A into echelon form, then find the rank,
We have,
A = 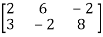
Apply, 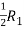
A = 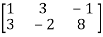
Apply 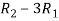 ,
,
A = 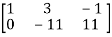
Apply 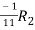
A = 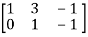
Apply 
A = 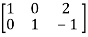
Hence the rank of the matrix will be 2.
Question-5: Find the inverse of the matrix  by row transformation?
by row transformation?
Let A=
By Gauss-Jordan method
We have 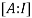
=
Apply 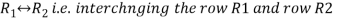

Apply 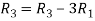 we get
we get

Apply  we get
we get
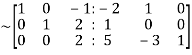
Apply 

Apply 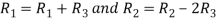
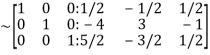
Hence 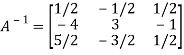
Question-6: : Find the inverse of the matrix  by row transformation?
by row transformation?
Let A= 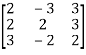
By Gauss-Jordan method
We have 
=
Apply  we get
we get
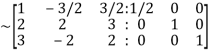
Apply 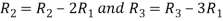
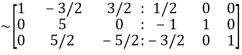
Apply 

Apply 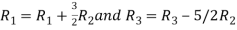
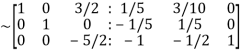
Apply 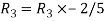

Apply 
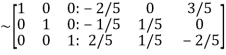
Hence 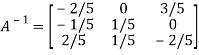
Question-7: Find the inverse of 
Let A= 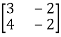
By Gauss Jordan method

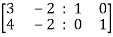
Apply 
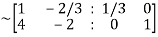
Apply

Apply 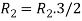

Apply 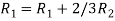
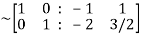
Hence the inverse of matrix A is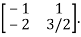
Question-8: Find the inverse of 
Let A= 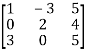
By Gauss-Jordan Method [A:I]
= 
Apply 

Apply 

Apply 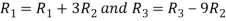

Apply 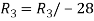
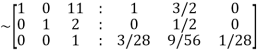
Apply 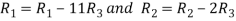

Hence the inverse of matrix A is 
Question-9: find the solution of the following linear equations.
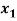 +
+ 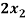 -
- 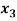 = 1
= 1
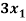 -
-  +
+ 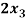 = 2
= 2
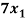 - 2
- 2 +
+  = 5
= 5
Sol. These equations can be converted into the form of matrix as below-
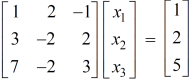
Apply the operation,  and
and 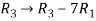 , we get
, we get
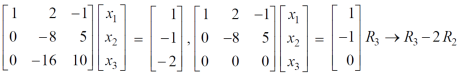
We get the following set of equations from the above matrix,
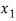 +
+ 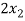 -
- 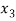 = 1 …………………..(1)
= 1 …………………..(1)
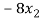 + 5
+ 5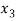 = -1 …………………(2)
= -1 …………………(2)
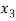 = k
= k
Put x = k in eq. (1)
We get,
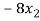 + 5k = -1
+ 5k = -1
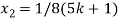
Put these values in eq. (1), we get
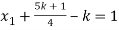
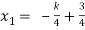
 and
and 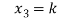
These equations have infinitely many solutions.
Question-10: solve the following system of equations by gauss-jordan method
 +
+  - 2
- 2 = 0
= 0
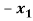 +
+ 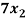 +
+ 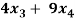 = 0
= 0
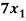 - 7
- 7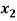 +
+ 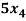 = 0
= 0
Sol. The given system of equations can be written in the form of matrices as follows,
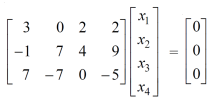
By applying operation - 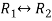 we get,
we get,
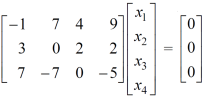
Now apply, 
We get,

Apply, 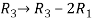

The set of the equations we get from above matrices,
 +
+ 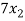 +
+  = 0 …………………..(1)
= 0 …………………..(1)
21 +
+  = 0 …………………………..(2)
= 0 …………………………..(2)
Suppose 
From equation-2, we get
21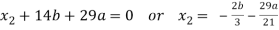
Now from equation-1:
-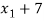 (
(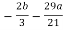 ) + 4b + 9a = 0
) + 4b + 9a = 0
We get,

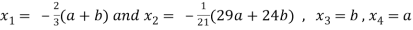
Question-11: solve the following system of equations by gauss-jordan method
2x + y + 2z = 10
X + 2y + z = 8
3x + y – z = 2
Sol. We will write the equations in matrix form as follows,

Now apply operation, 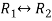

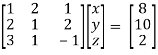
Apply 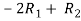 , we get,
, we get,

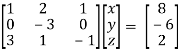
Apply, 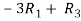 , we get,
, we get,


Apply,  / -3 , we get
/ -3 , we get

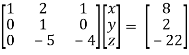
Apply 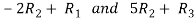

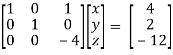
Apply  / -4, we get
/ -4, we get

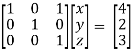
Finally apply 
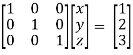
Therefore the solution of the set of linear equations will be,
x = 1 , y = 2 , z = 3
Question-12: solve the following system of equations by gauss-jordan method.
6a + 8b +6c + 3d = -3
6a – 8b + 6c – 3d = 3
8b - 6d = 6
Sol. Change the system of linear equations into matrix form,
The augmented matrix format will be,

Apply 
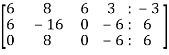
Apply 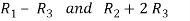
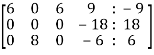
Apply 

Apply 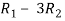 and
and 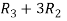

Apply 

Apply 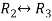

This is the reduced row echelon form,
The system of linear equations becomes,
a + c = 0
b = 0
d = -1
Suppose c = t be a free variable,
Then the solution will be,
a = -t
b = 0
c = t
d = -1
For any number ‘t’.
Question-13: Find out the Eigen values and Eigen vectors of  ?
?
The Characteristics equation is given by 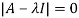
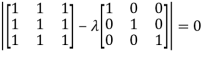

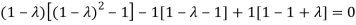

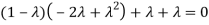
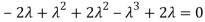
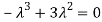
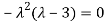
Or 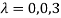
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 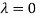 is
is
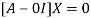
Where X is the column matrix of order 3 i.e.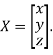
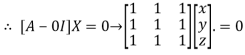
This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1)=2 linearly independent solutions.
Let 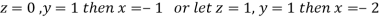
Thus the Eigen vectors corresponding to the Eigen value 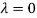 are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 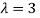 is
is

Where X is the column matrix of order 3 i.e.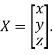
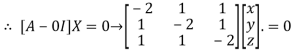
This implies that 
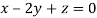

Taking last two equations we get
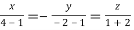
Or 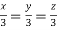
Thus the Eigen vectors corresponding to the Eigen value  are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Question-14: Find out the Eigen values and Eigen vectors of 
Let A =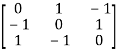
The characteristics equation of A is  .
.
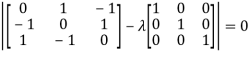
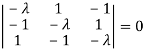
Or 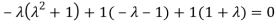
Or 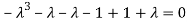
Or 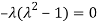
Or 
The Eigen vector corresponding to Eigen value 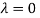 is
is
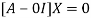
Where X is the column matrix of order 3 i.e.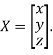

Or 

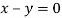
On solving we get 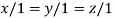
Thus the Eigen vectors corresponding to the Eigen value 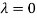 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value  is
is

Where X is the column matrix of order 3 i.e.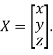
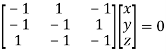
Or 


On solving  or
or  .
.
Thus the Eigen vectors corresponding to the Eigen value  is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 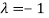 is
is
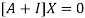
Where X is the column matrix of order 3 i.e.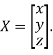

Or 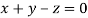
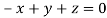
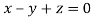
On solving we get 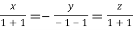 or
or 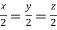 .
.
Thus the Eigen vectors corresponding to the Eigen value 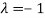 is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Question-15: Verify the Cayley-Hamilton theorem and find the inverse.

The characteristics equation of A is 

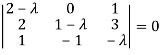
Or 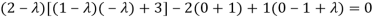
Or 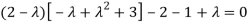
Or 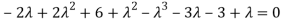
Or 
Or 
By Cayley-Hamilton theorem 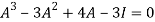
L.H.S. 
=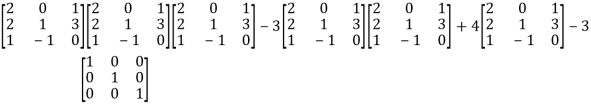
=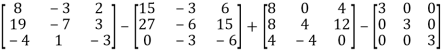
=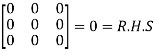
Multiply both side with  in
in 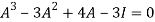

Or 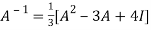
Or 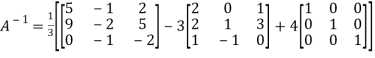
=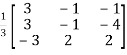
Question-16: : Diagonalise the matrix 
Let A= 
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values  .
.
Then  and
and 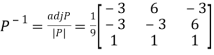
Also we know that