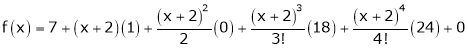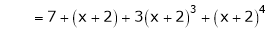Question bank (unit-2)

Question-1: : Show that

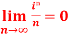
Sol. For  ϵ > 0 , we need to find an integer N such that ,

                                      |

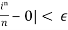
For all n≥N , since |i|=1  we need 1/n< ϵ , so that we choose any N>1 / ϵ>0 , for all  n≥N , we find that

Here |i| = 1 , then

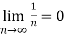
Question-2: show that

                                     = 1

Sol. 

Let   Sn = 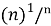- 1 for all n >0 , here Sn ≥ 0 for all positive n , therefore

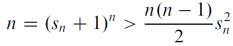
For all n>0 ,

       for all n > 1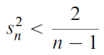                                            

From Sandwich theorem, we get,

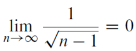
Question-3: check whether the sequence is bounded monotonic sequence or not.

Sol. This is the decreasing sequence, hence we can say that this is monotonic for every n.

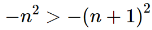
As we can notice here that the terms in this sequence will be either zero or negative , so that the sequence is bounded above.

Suppose m = 0 then,

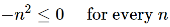
This sequence is not bounded below ,

Hence we can not say that the sequence is bounded.

Question-4: check whether the series 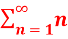is convergent or divergent. Find its value in case of convergent.

Sol.  As we know that,

           Sn =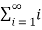 

Therefore,

         Sn =   

Now find out the limit of the sequence,

                                                        = ∞

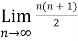Here the value of the limit is infinity, so that the series is divergent as sequence diverges.

Question-5: : check whether the series  is convergent or divergent.   

Sol. The general formula can be written as,

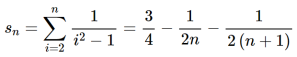
We get on applying limits,

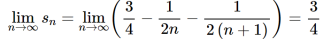
This is the convergent series and its value is 3 / 4

Question-6: Show that the harmonic series is divergent.

Sol. First we will expand its three terms ,

                                         = 1+ +

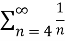
We get,

Here if we subtract a finite number from a divergent series , then the resulting series will not be affected by this number.

Therefore we can say that  is the divergent series which is also a harmonic series.

Question-7: determine the following series is convergent or divergent.

Sol.  By using integral test

    = ∞

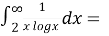
By the integral test, given series is divergent as

Question-8: Test the series by integral test-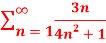

Sol. Here 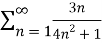is positive and decreases when we increase n ,

      Now apply integral test,

Let,          

X = 1 , t = 5 and x = ∞ , t = ∞,

Now,

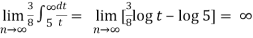
So by integral test,

The series is divergent.

Question-9: Test the convergence of the following series:

Sol.

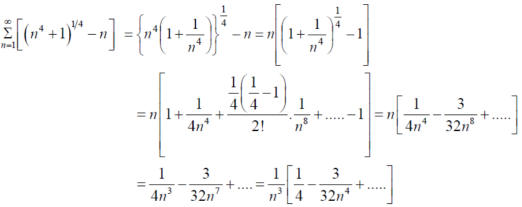
Here we take,

Which not zero and finite ,

So by comparison test , and both converges or diverges, but by p-series test

Is convergent . So that  is convergent.

Question-10 Test the convergence of the series:

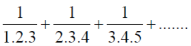
Sol.

By p-series test,

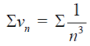
Is convergent ( p = 3>1).

Question-11: : Test the series:

Sol. The series is,

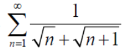
Now,

Take,

Which is finite and not zero.

Which is finite and not zero.

By comparison test and 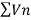converge or diverge together.

But,

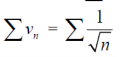
Is divergent. ( p = ½)

So that is divergent.

Question-12: Test the series for convergence.

Sol.  For all n>= 0    let,

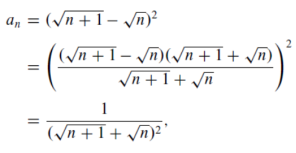
And let,

For all n>0, since

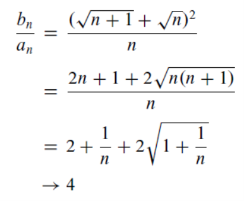
It follows,

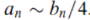
By limit comparison test , the series is divergent

Question-13: : Test the convergence of the following series.

Sol. Neglecting the first term the series can be written as,

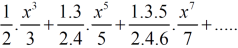
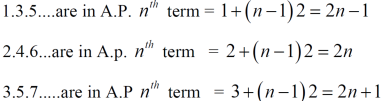
So that,

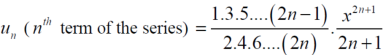
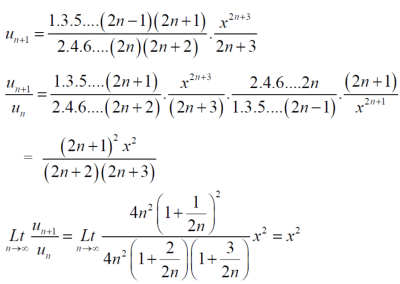
By ratio test  converges if |x|<1 and diverges if |x|>1, but if |x| = 1 the the test fails,

 Then ,

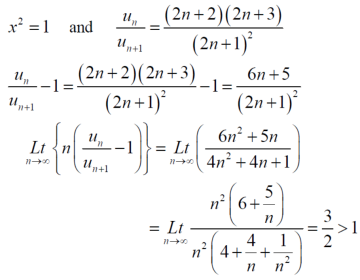
By Raabes’s test 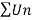 converges hence the given series is convergent when |x|≤ 1 and divergent If |x| >1.

Question-14: Test the nature of the following series:

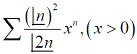
Sol.

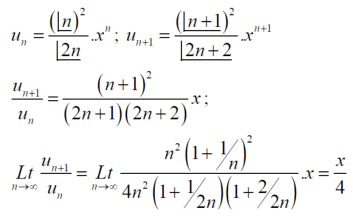
By ration test 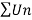 is convergent when (x/4)<1 and divergent when x>4, when x= 4,

The rario test fails, then

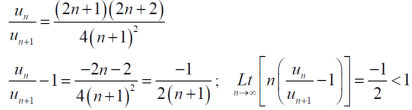
By Rabee’s test is convergent , hence the given series is convergent when x<4 and divergent If x >=4.

Question-15: Test the convergence of the series whose nth term is given below-

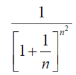
Sol.

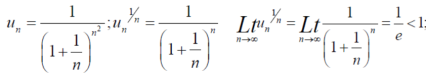
By root test is convergent.

Question-16: Test for absolute convergence:

Sol. Let the series is ,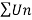

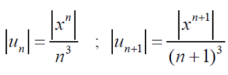
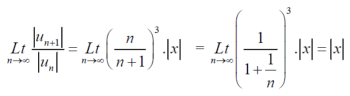
By ratio test,

is convergent , if |x|<1.

is absolutely convergent if |x|< 1.

Question-17: Prove that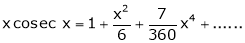

Solution:

Here f(x) = x cosec x

=

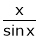
Now we know that

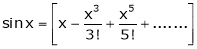
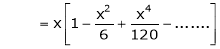
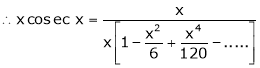
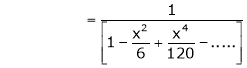
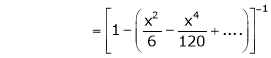
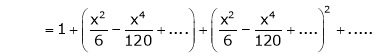
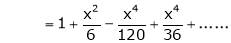
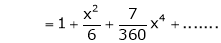
Question-18: Show that

Solution:

Here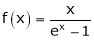

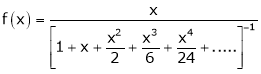
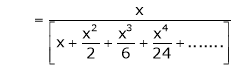
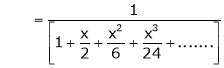
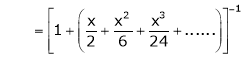
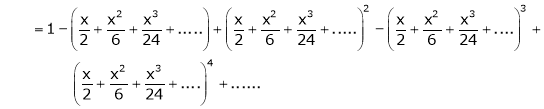
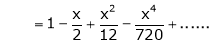
Thus

Question-19: Expand in power of (x – 3)

Solution:

Let

Here a = 3

Now by Taylor’s series expansion,

… (1)

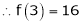
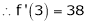
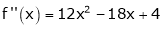
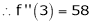
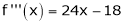
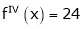
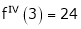
equation (1) becomes.

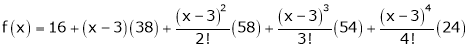
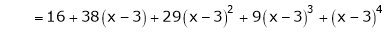
Question-20: Using Taylors series method expand

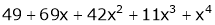in powers of (x + 2)

Solution:

Here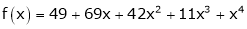

a = -2

By Taylors series,

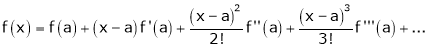… (1)

Since

,, …..

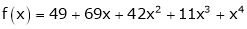
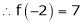
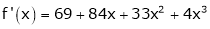
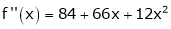
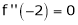
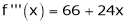
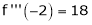
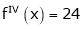
Thus equation (1) becomes