Question bank(unit-3)
Question bank(unit-3)
Question bank(unit-3)
Question-1: Find the fourier series of the function f(x) = x where 0 < x < 2 π
Sol. We know that, from fourier series,
f(x) =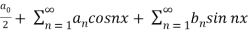 
First we will find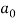 
,
Now,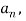 
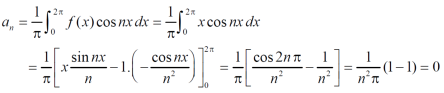
And 
,
Put these value in fourier series, we get
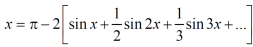
Question-2: Find the fourier series for f(x) = x / 2 over the interval 0 < x < 2π
And has period 2π
Sol. First we will find
= 
= 
=
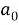= π
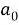= π
Similarly,
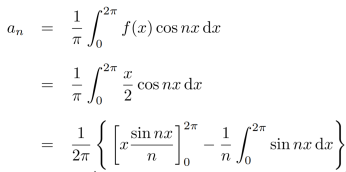
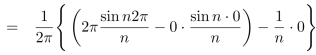
Which gives,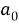 
= 0
Now,
We get, 
We know that, the fourier series
Put these values in fourier series, we get
Question-3: Find the Fourier series of f(x) = x in the interval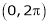 
Solution:
Here 
; 
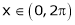
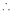It’s Fourier series is given by
… (1)
Where
&
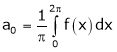
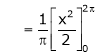
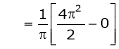
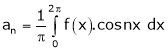
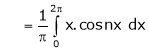
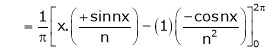
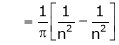
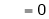
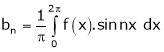
Hence the required Fourier series is
- Question-4: Find the Fourier series for
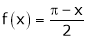in the interval 
Hence deduce that
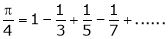
Solution:
Here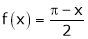 
;
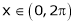
Hence it’s Fourier series is,
… (1)
Where
&
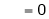
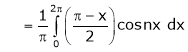
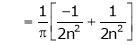
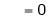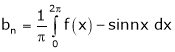
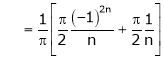
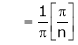
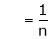
Hence equation (1) becomes
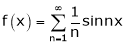
Put 
we get
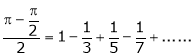
i.e. 
Question-5: Find a Fourier series expansion in the interval 
for
;
;
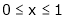
Solution:
Here
;
;
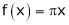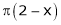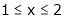
Hence it’s Fourier series expansion is,
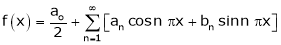… (1)
Where
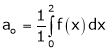
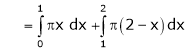
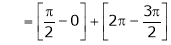
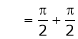
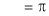
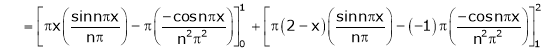
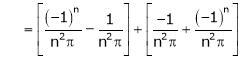
And
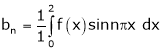
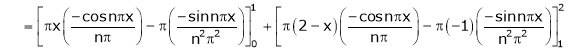
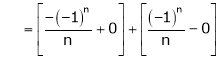
Hence equation (1) becomes
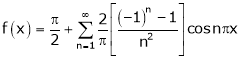
Question-6: Find a Fourier series of
;
;
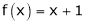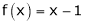Solution:
Here
;
;
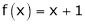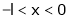
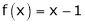Here f(x) is odd function Hence we get half range sine series i.e.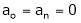 
… (1)
Where
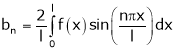
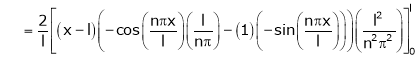
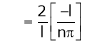
Hence equation (1) becomes,
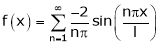
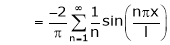
Question-7: Find the fourier expression of f(x) = x³ for –π < x < π.
Sol.
Here, we can see that f(x) Is an odd function
So that,
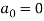and 
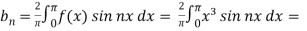
We will use here ,
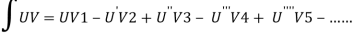
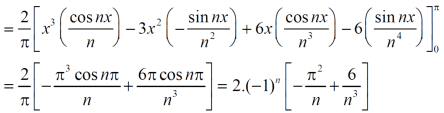
We get the value of f(x),
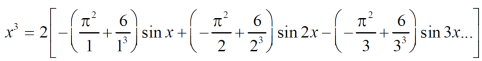
Question-8: Find the Fourier series expansion of the periodic function of period 2π.
f(x) = x² , -π≤x≤π
Sol. The given function is even, so that,
We will find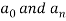 
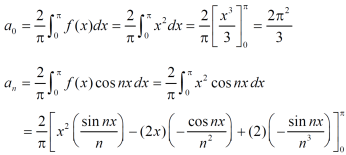
The fourier series will be ,
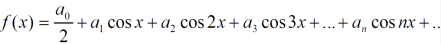
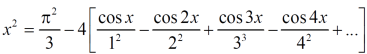
Question-9: Find a Fourier series for
;
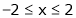
Solution:
Here
;
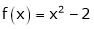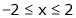
Since f(x) is even function hence 
It’s Fourier series is
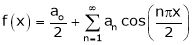… (1)
Where
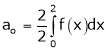
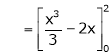
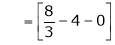
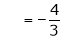
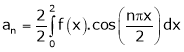
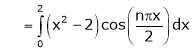
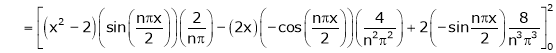
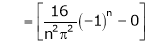
Hence equation (1) becomes,
Question-10: Find half range cosine series of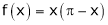 
in the interval 
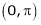and hence deduce that
a)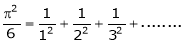 
b) 
Solution:
Here
;
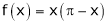Hence it’s half range cosine series is,
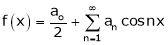… (1)
Where
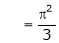
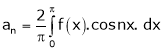
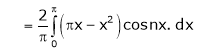
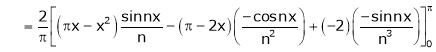
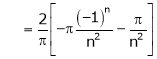
Hence equation (1) becomes,
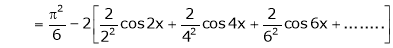
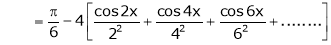… (2)
Put x = 0, we get
Hence the result
Put 
we get,
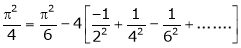
i.e. 
