Unit-1
Partial differentiation and its Applications
Question Bank
Question-1: Calculate  and
and  for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate  treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] -  5y²] +
5y²] +  [2xy] -
[2xy] - 8x] +
8x] + 4y] -
4y] -  20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] -  5y²] +
5y²] +  [2xy] -
[2xy] - 8x] +
8x] + 4y] -
4y] -  20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Question-2: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Sol. 3x²y² - y⁵,
3x²y² - y⁵,  2x³y – 5xy⁴,
2x³y – 5xy⁴,
 =
=  = 6xy²
= 6xy²
 =
=  2x³ - 20xy³
2x³ - 20xy³
 =
=  = 6x²y – 5y⁴
= 6x²y – 5y⁴
 =
=  = 6x²y - 5y⁴
= 6x²y - 5y⁴
Question-3: if  , then show that-
, then show that- 
Sol. Here we have,
u =  …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get
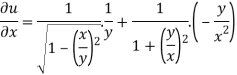
= 
Or
 ………………..(2)
………………..(2)
And now,

= 
 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
 = 0
= 0
Hence proved.
Question-4: If u(x,y,z) = log( tan x + tan y + tan z) , then prove that ,
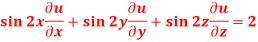
Sol. Here we have,
u(x,y,z) = log( tan x + tan y + tan z) ………………..(1)
Diff. Eq.(1) w.r.t. x , partially , we get
 ……………..(2)
……………..(2)
Diff. Eq.(1) w.r.t. y , partially , we get
 ………………(3)
………………(3)
Diff. Eq.(1) w.r.t. z , partially , we get
 ……………………(4)
……………………(4)
Now multiply eq. 2 , 3 , 4 by sin 2x , sin 2y , sin 2z respectively and adding , in order to get the final result,
We get,
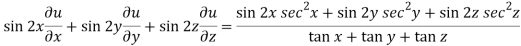
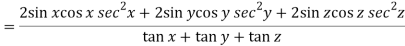
= 
So that,
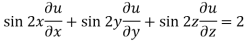
Hence proved.
Question-5: if ∅ is a differentiable function such that y = ∅(x) satisfies the equation
x³ + y³ +sin xy = 0 then find  .
.
Sol. Suppose f(x,y) = x³ + y³ +sin xy
Then,
fᵡ= 3x² + y cosxy
Fy = 2y + x cosxy
So,
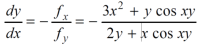
Question-6: let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find  .
.
Sol. : . =
. = 
Where, f1 =  , f2 =
, f2 = 
In this example f1 = 4 , f2 = 3
Also,  3t² + 2t ,
3t² + 2t , 
 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(
= 21t² + 2t – 3
Question-7: if w = x² + y – z + sintand x + y = t, find
(a)  y,z
y,z
(b)  t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x²+ y - z + sin (x + y).
Therefore,
 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y) (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
Thus t, z = 2x - 1
t, z = 2x - 1
Question-8: If z is the function of x and y , and x =  , y =
, y =  , then prove that,
, then prove that,
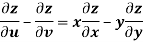
Sol. Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
 ……………….(1)
……………….(1)
And,
 ………………..(2)
………………..(2)
Also there is,
x =  and y =
and y =  ,
,
Now,
 ,
,  ,
,  ,
, 
From equation(1) , we get
 ……………….(3)
……………….(3)
And from eq. (2) , we get
 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
 =
=  )
) – (
– (
= x
Hence proved.
Question-9: If u = xyz , v = x² + y² + z² and w = x + y + z, then find J = 
Sol. Here u ,v and w are explicitly given , so that first we calculate
J’ = 
J’ =  =
= 
= yz(2y-2z) – zx(2x – 2z) + xy (2x – 2y) = 2[yz(y-z)-zx(x-z)+xy(x-y)]
= 2[x²y - x²z - xy² + xz² + y²z - yz²]
= 2[x²(y-z) - x(y² - z²) + yz (y – z)]
= 2(y – z)(z – x)(y – x)
= -2(x – y)(y – z)(z – x)
By the property,
JJ’ = 1
J = 
Question-10: Find the Taylor’s expansion of  about (1 , 1) up to second degree term.
about (1 , 1) up to second degree term.
Sol. We have,
At (1 , 1)
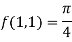
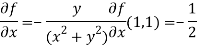
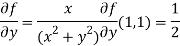
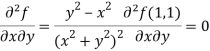
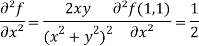
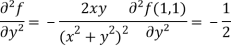
Now by using Taylor’s theorem-
 ……
……
Suppose 1 + h = x then h = x – 1
1 + k = y then k = y - 1
 ……
……
 =
= 
 ……..
……..
Question-11: Calculate the percentage increase in the pressure p corresponding to a reduction
Of 1/2 % in the volume V, if the p and V are related by  = C, where C is a constant.
= C, where C is a constant.
Sol.
Here we have-
 = C
= C
Taking log on both sides,
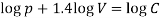
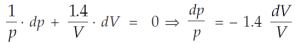
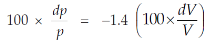
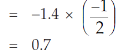
Hence increase in the pressure p = 0.7 percent
Question-12: Find the maximum and minimum point of the function
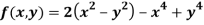
Partially differentiating given equation with respect to and x and y then equate them to zero
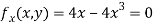
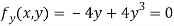
On solving above we get 
Also 
Thus we get the pair of values (0,0), ( ,0) and (0,
,0) and (0,
Now, we calculate
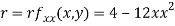
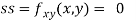
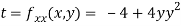
At the point (0,0)
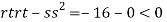
So function has saddle point at (0,0).
At the point (
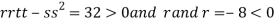
So the function has maxima at this point ( .
.
At the point (0,
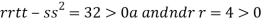
So the function has minima at this point (0, .
.
At the point (
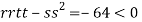
So the function has an saddle point at (
Question-13: Find the point on plane  nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
Solution:
Let  be the point on sphere
be the point on sphere  which is nearest to the point
which is nearest to the point  . Then shortest distance.
. Then shortest distance.
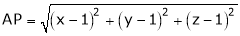
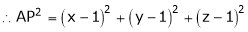
 Let
Let 
Under the condition  … (1)
… (1)
 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have
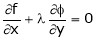
 … (2)
… (2)
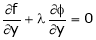
 … (3)
… (3)
i.e.  &
&
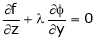
 … (4)
… (4)
From (2) we get 
From (3) we get 
From (4) we get 
 Equation (1) becomes
Equation (1) becomes
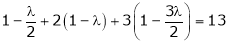
i.e. 
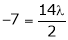
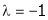
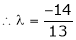
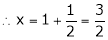
y = 2
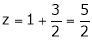
Question-14: Solve the differential equation-
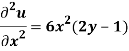
Given the boundary condition that-
At x = 0, 
Sol.
Here we have-
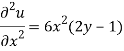
On integrating partially with respect to x, we get-
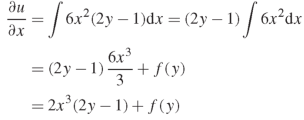
Here f(y) is an arbitrary constant.
Now form the boundary condition-
When x = 0,
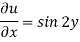
Hence-
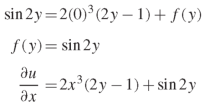
On integrating partially w.r.t.x, we get-
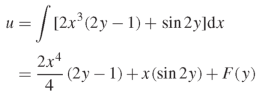
Question-15: Solve-
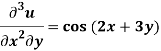
Sol.
Here we have-
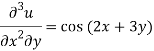
Integrate w.r.t. x, we get-
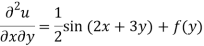
Integrate w.r.t. x, we get-
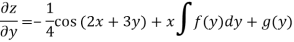
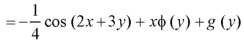
Integrate w.r.t. y, we get-
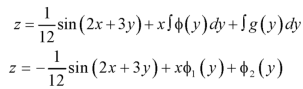
Question-16: Solve-
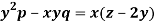
Sol.
We have-
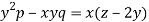
Then the auxiliary equations are-
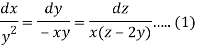
Consider first two equations only-
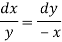
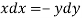
On integrating
 …….. (2)
…….. (2)
Now consider last two equations-
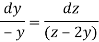
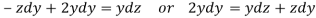
On integrating we get-
 …………… (3)
…………… (3)
From equation (2) and (3)-
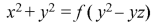
Question-17: Solve-

Sol.
Let u = x + by
So that-
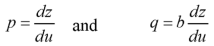
Put these values of p and q in the given equation, we get-
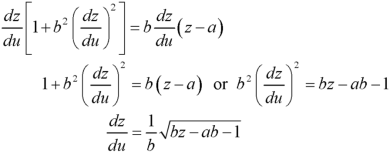
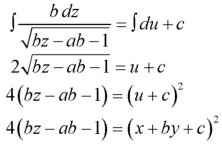
Question-18: Solve-
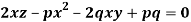
Sol.
Let
Charpit’s subsidiary equations are-
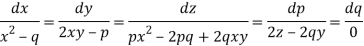
So that- dq = 0 or q = a
On putting q = a in (1) we get-
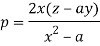
Such that-
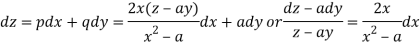
Integrating
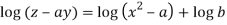
Or
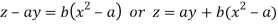
Which is the required solution.