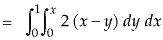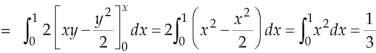Unit-4
Multiple integrals
Question Bank
Question-1: Evaluate 
Sol. Let us suppose the integral is I,
I = 
Put c = 1 – x in I, we get
I = 
Suppose , y = ct
Thendy = c
Now we get,
I = 
I = 
I = 
I = 
I =
As we know that by beta function,

Which gives,
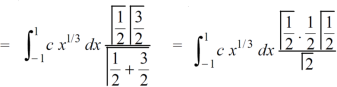
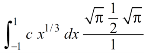

Now put the value of c, we get
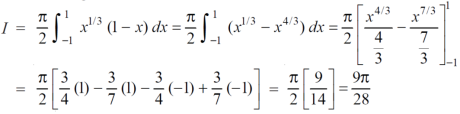
Question-2: Evaluate-
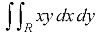
Where R is the quadrant of the circle  .
.
Sol.
Suppose the region of integration is the first quadrant of the circle OAB.
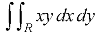
(
First we will integrate w.r.t. x then w.r.t. y-
The limits for y are 0 and  and limits for x are 0 to a.
and limits for x are 0 to a.
We get-
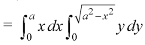
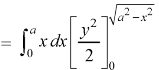
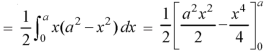
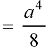
Question-3: Evaluate-
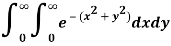
By changing into polar coordinates.
Sol.
We have

The limits of x and y are 0 to 
Hence the region of integration is in the first quadrant,
The region is covered by the radius strip from r = 0 to r = ∞ and it starts from θ = 0 to θ = π/2
Hence the integral becomes-
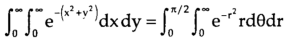
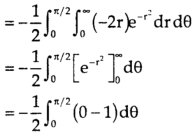
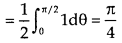
Question-4: Evaluate  Where V is annulus between the spheres
Where V is annulus between the spheres 
And  (
( )
)
Solution: It is convenient to transform the triple integral into spherical polar co-ordinate by putting
 ,
,  ,
, 
 , dxdydz=
, dxdydz= sin
sin drd
drd d
d ,
,
 and
and
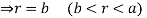
For the positive octant, r varies from r =b to r =a ,  varies from
varies from 
And varies from
varies from 
I= 
= 8
=8
=8
=8
=8 log
= 8 log
I= 8 log I = 4 log
I = 4 log
Question-5: Find Volume of the tetrahedron bounded by the co-ordinate planes and the plane

Solution: Volume = ………. (1)
………. (1)
Put  ,
, 
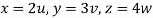
From equation (1) we have
V = 
=24
=24 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 
= =
= = 4
= 4
Volume =4
Question-6:
Evaluate 
Solution:- Put
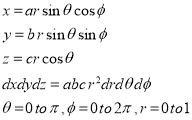
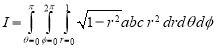
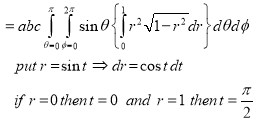
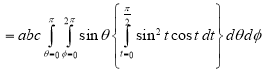
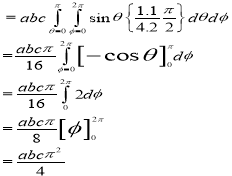
Question-7: If  , then show that
, then show that
1. 
2. 
Sol.
Suppose  and
and 
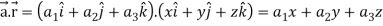
Now taking L.H.S,
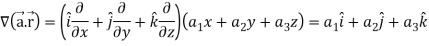
Which is 
Hence proved.
2. 
So that

Question-8: Evaluate  , where S is the surface of the sphere
, where S is the surface of the sphere  in the first octant.
in the first octant.
Sol. Here-
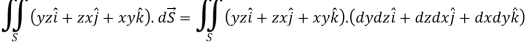
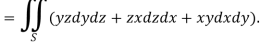
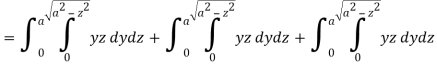
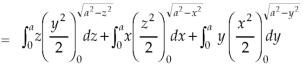
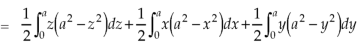
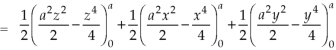
Which becomes-
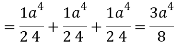
Question-9: Evaluate  if V is the region in the first octant bounded by
if V is the region in the first octant bounded by  and the plane x = 2 and
and the plane x = 2 and  .
.
Sol.
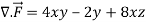
x varies from 0 to 2
The volume will be-
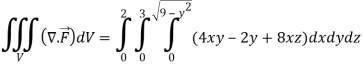
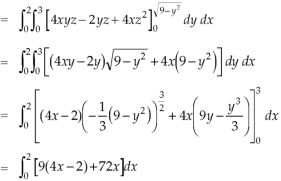
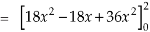
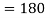
Question-10: Evaluate  by using Green’s theorem, where C is a triangle formed by
by using Green’s theorem, where C is a triangle formed by 
Sol. First we will draw the figure-
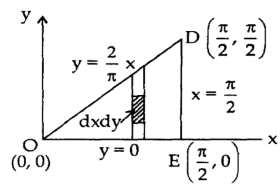
Here the vertices of triangle OED are (0,0), (
Now by using Green’s theorem-
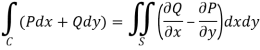
Here P = y – sinx, and Q =cosx
So that-
 and
and
Now-
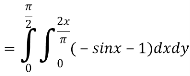

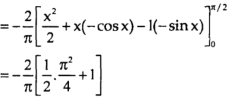
= 
Which is the required answer.
Question-11: Prove the following by using Gauss divergence theorem-
1. 
2. 
Where S is any closed surface having volume V and 
Sol. Here we have by Gauss divergence theorem-
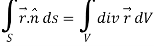
Where V is the volume enclose by the surface S.
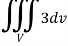
We know that-
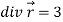
= 3V
2.
Because 
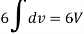
Question-12: If  and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate
and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate  by using Stoke’s theorem.
by using Stoke’s theorem.
Sol. Here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and 
Now,
Curl 
Curl 
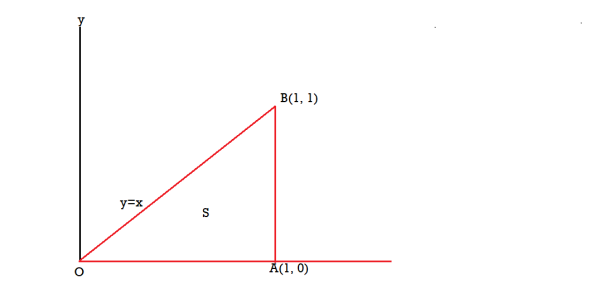
The equation of the line OB is y = x
Now by stoke’s theorem,