SECTION B

1. What is an Algorithm and what are the Characteristics of an Algorithm?

An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer. The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task. It is not the complete program or code; it is just a solution (logic) of a problem, which can be represented either as an informal description using a Flowchart or Pseudocode.

Characteristics of an Algorithm

The following are the characteristics of an algorithm:

• Input: An algorithm has some input values. We can pass 0 or some input value to an algorithm.
• Output: We will get 1 or more output at the end of an algorithm.
• Unambiguity: An algorithm should be unambiguous which means that the instructions in an algorithm should be clear and simple.
• Finiteness: An algorithm should have finiteness. Here, finiteness means that the algorithm should contain a limited number of instructions, i.e., the instructions should be countable.
• Effectiveness: An algorithm should be effective as each instruction in an algorithm affects the overall process.
• Language independent: An algorithm must be language-independent so that the instructions in an algorithm can be implemented in any of the languages with the same output.

Dataflow of an Algorithm

• Problem: A problem can be a real-world problem or any instance from the real-world problem for which we need to create a program or the set of instructions. The set of instructions is known as an algorithm.
• Algorithm: An algorithm will be designed for a problem which is a step by step procedure.
• Input: After designing an algorithm, the required and the desired inputs are provided to the algorithm.
• Processing unit: The input will be given to the processing unit, and the processing unit will produce the desired output.
• Output: The output is the outcome or the result of the program.

2.       Why do we need Algorithms?

We need algorithms because of the following reasons:

• Scalability: It helps us to understand the scalability. When we have a big real-world problem, we need to scale it down into small-small steps to easily analyze the problem.
• Performance: The real-world is not easily broken down into smaller steps. If the problem can be easily broken into smaller steps means that the problem is feasible.

Let's understand the algorithm through a real-world example. Suppose we want to make a lemon juice, so following are the steps required to make a lemon juice:

Step 1: First, we will cut the lemon into half.

Step 2: Squeeze the lemon as much you can and take out its juice in a container.

Step 3: Add two tablespoon sugar in it.

Step 4: Stir the container until the sugar gets dissolved.

Step 5: When sugar gets dissolved, add some water and ice in it.

Step 6: Store the juice in a fridge for 5 to minutes.

Step 7: Now, it's ready to drink.

The above real-world can be directly compared to the definition of the algorithm. We cannot perform the step 3 before the step 2, we need to follow the specific order to make lemon juice. An algorithm also says that each and every instruction should be followed in a specific order to perform a specific task.

3.       What are the different Approaches of Algorithm?

The following are the approaches used after considering both the theoretical and practical importance of designing an algorithm:

• Brute force algorithm: The general logic structure is applied to design an algorithm. It is also known as an exhaustive search algorithm that searches all the possibilities to provide the required solution. Such algorithms are of two types:
  1. Optimizing: Finding all the solutions of a problem and then take out the best solution or if the value of the best solution is known then it will terminate if the best solution is known.
  2. Sacrificing: As soon as the best solution is found, then it will stop.
• Divide and conquer: It is a very implementation of an algorithm. It allows you to design an algorithm in a step-by-step variation. It breaks down the algorithm to solve the problem in different methods. It allows you to break down the problem into different methods, and valid output is produced for the valid input. This valid output is passed to some other function.
• Greedy algorithm: It is an algorithm paradigm that makes an optimal choice on each iteration with the hope of getting the best solution. It is easy to implement and has a faster execution time. But, there are very rare cases in which it provides the optimal solution.
• Dynamic programming: It makes the algorithm more efficient by storing the intermediate results. It follows five different steps to find the optimal solution for the problem:
  1. It breaks down the problem into a subproblem to find the optimal solution.
  2. After breaking down the problem, it finds the optimal solution out of these subproblems.
  3. Stores the result of the subproblems is known as memorization.
  4. Reuse the result so that it cannot be recomputed for the same subproblems.
  5. Finally, it computes the result of the complex program.
• Branch and Bound Algorithm: The branch and bound algorithm can be applied to only integer programming problems. This approach divides all the sets of feasible solutions into smaller subsets. These subsets are further evaluated to find the best solution.
• Randomized Algorithm: As we have seen in a regular algorithm, we have predefined input and required output. Those algorithms that have some defined set of inputs and required output, and follow some described steps are known as deterministic algorithms. What happens that when the random variable is introduced in the randomized algorithm?. In a randomized algorithm, some random bits are introduced by the algorithm and added in the input to produce the output, which is random in nature. Randomized algorithms are simpler and efficient than the deterministic algorithm.
• Backtracking: Backtracking is an algorithmic technique that solves the problem recursively and removes the solution if it does not satisfy the constraints of a problem.

4.       What is the Algorithm Complexity?

The performance of the algorithm can be measured in two factors:

• Time complexity: The time complexity of an algorithm is the amount of time required to complete the execution. The time complexity of an algorithm is denoted by the big O notation. Here, big O notation is the asymptotic notation to represent the time complexity. The time complexity is mainly calculated by counting the number of steps to finish the execution. Let's understand the time complexity through an example.

1. Sum=0;  
2. // Suppose we have to calculate the sum of n numbers.  
3. For i=1 to n  
4. Sum=sum+i;  
5. // when the loop ends then sum holds the sum of the n numbers  
6. Return sum;  

In the above code, the time complexity of the loop statement will be atleast n, and if the value of n increases, then the time complexity also increases. While the complexity of the code, i.e., return sum will be constant as its value is not dependent on the value of n and will provide the result in one step only. We generally consider the worst-time complexity as it is the maximum time taken for any given input size.

• Space complexity: An algorithm's space complexity is the amount of space required to solve a problem and produce an output. Similar to the time complexity, space complexity is also expressed in big O notation.

For an algorithm, the space is required for the following purposes:

1. To store program instructions
2. To store constant values
3. To store variable values
4. To track the function calls, jumping statements, etc.

Auxiliary space: The extra space required by the algorithm, excluding the input size, is known as an auxiliary space. The space complexity considers both the spaces, i.e., auxiliary space, and space used by the input.

So,

Space complexity = Auxiliary space + Input size.

5.     What are the types of Algorithms?

The following are the types of algorithm:

• Search Algorithm
• Sort Algorithm

Search Algorithm

On each day, we search for something in our day to day life. Similarly, with the case of computer, huge data is stored in a computer that whenever the user asks for any data then the computer searches for that data in the memory and provides that data to the user. There are mainly two techniques available to search the data in an array:

• Linear search
• Binary search

Linear Search

Linear search is a very simple algorithm that starts searching for an element or a value from the beginning of an array until the required element is not found. It compares the element to be searched with all the elements in an array, if the match is found, then it returns the index of the element else it returns -1. This algorithm can be implemented on the unsorted list.

Binary Search

A Binary algorithm is the simplest algorithm that searches the element very quickly. It is used to search the element from the sorted list. The elements must be stored in sequential order or the sorted manner to implement the binary algorithm. Binary search cannot be implemented if the elements are stored in a random manner. It is used to find the middle element of the list.

Sorting Algorithms

Sorting algorithms are used to rearrange the elements in an array or a given data structure either in an ascending or descending order. The comparison operator decides the new order of the elements.

Why do we need a sorting algorithm?

• An efficient sorting algorithm is required for optimizing the efficiency of other algorithms like binary search algorithm as a binary search algorithm requires an array to be sorted in a particular order, mainly in ascending order.
• It produces information in a sorted order, which is a human-readable format.
• Searching a particular element in a sorted list is faster than the unsorted list.

6.     Explain Flowchart with examples

Flowchart could be a delineate illustration of sequence of logical steps of a program. Flowcharts use easy geometric shapes to depict processes and arrows to indicate relationships and process/data flow.

Flowchart Symbols

Here is a chart for some of the common symbols used in drawing flowcharts.

Symbol	Symbol Name	Purpose
	Start/Stop	Used at the beginning and end of the algorithm to show start and end of the program.
	Process	Indicates processes like mathematical operations.
	Input/ Output	Used for denoting program inputs and outputs.
	Decision	Stands for decision statements in a program, where answer is usually Yes or No.
	Arrow	Shows relationships between different shapes.
	On-page Connector	Connects two or more parts of a flowchart, which are on the same page.
	Off-page Connector	Connects two parts of a flowchart which are spread over different pages.

Guidelines for Developing Flowcharts

These area unit some points to stay in mind whereas developing a flow chart flow chart

•Flowchart will have only 1 begin and one stop image

•On-page connectors area unit documented victimization numbers

•Off-page connectors area unit documented victimization alphabets

•General flow of processes is prime to bottom or left to right

•Arrows mustn't cross one another

Example Flowcharts

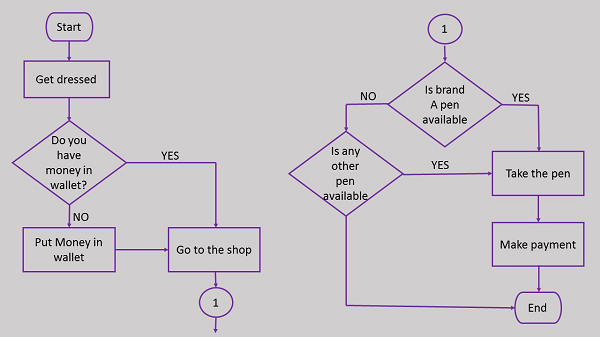
Here is the flowchart for going to the market to purchase a pen.

Here is a flowchart to calculate the average of two numbers.

7.     Show with example Using the Python Interactive Shell

With the Python interactive interpreter it is easy to check Python commands. The Python interpreter can be invoked by typing the command "python" without any parameter followed by the "return" key at the shell prompt:

Python

Python comes back with the following information:

$ python

Python 2.7.11 (default, Mar 27 2019, 22:11:17)

[GCC 7.3.0] :: Anaconda, Inc. On linux

Type "help", "copyright", "credits" or "license" for more information.

A closer look at the output above reveals that we have the wrong Python version. We wanted to use Python 3.x, but what we got is the installed standard of the operating system, i.e. version 2.7.11+.

The easiest way to check if a Python 3.x version is installed: Open a Terminal. Type in python but no return. Instead, type the "Tab" key. You will see possible extensions and other installed versions, if there are some:

Bernd@venus:~$ $ python

Python             python3            python3.7-config   python-config

Python2            python3.6          python3.7m         pythontex

Python2.7          python3.6-config   python3.7m-config  pythontex3

Python2.7-config   python3.6m         python3-config     python-whiteboard

Python2-config     python3.6m-config  python3m          

Python2-pbr        python3.7          python3m-config  

Bernd@venus:~$ python

If no other Python version shows up, python3.x has to be installed. Afterwards, we can start the newly installed version by typing python3:

$ python3

Python 3.6.7 (default, Oct 22 2018, 11:32:17)

[GCC 8.2.0] on linux

Type "help", "copyright", "credits" or "license" for more information.

Once the Python interpreter is started, you can issue any command at the command prompt ">>>". Let's see, what happens, if we type in the word "hello":

Hello

---------------------------------------------------------------------------

NameErrorTraceback (most recent call last)

<ipython-input-1-f572d396fae9> in <module>

----> 1 hello

NameError: name 'hello' is not defined

Of course, "hello" is not a proper Python command, so the interactive shell returns ("raises") an error.

The first real command we will use is the print command. We will create the mandatory "Hello World" statement:

Print("Hello World")

Hello World

It couldn't have been easier, could it? Oh yes, it can be written in a even simpler way. In the Interactive Python Interpreter - but not in a program - the print is not necessary. We can just type in a string or a number and it will be "echoed"

"Hello World"

Output::

'Hello World'

3

Output::

3

8.     Write an example of The Shell as a Simple Calculator

In the following example we use the interpreter as a simple calculator by typing an arithmetic expression:

4.567 * 8.323 * 17

Output::

646.189397

Python follows the usual order of operations in expressions. The standard order of operations is expressed in the following enumeration:

• Exponents and roots
• Multiplication and division
• Addition and subtraction

In other words, we don't need parentheses in the expression "3 + (2 * 4)":

3 + 2 * 4

Output::

11

The most recent output value is automatically stored by the interpreter in a special variable with the name "_". So we can print the output from the recent example again by typing an underscore after the prompt:

_

Output::

11

The underscore can be used in other expressions like any other variable:

_ * 3

Output::

33

The underscore variable is only available in the Python shell. It's NOT available in Python scripts or programs.

9.     What is the Numbers data type in python?

Number stores numeric values. The integer, float, and complex values belong to a Python Numbers data-type. Python provides the type() function to know the data-type of the variable. Similarly, the isinstance() function is used to check an object belongs to a particular class.

Python creates Number objects when a number is assigned to a variable. For example;

1. a = 5  
2. Print("The type of a", type(a))  
3.  
4. b = 40.5  
5. Print("The type of b", type(b))  
6.  
7. c = 1+3j  
8. Print("The type of c", type(c))  
9. Print(" c is a complex number", isinstance(1+3j,complex))  

Output:

The type of a <class 'int'>

The type of b <class 'float'>

The type of c <class 'complex'>

c is complex number: True

Python supports three types of numeric data.

1. Int - Integer value can be any length such as integers 10, 2, 29, -20, -150 etc. Python has no restriction on the length of an integer. Its value belongs to int
2. Float - Float is used to store floating-point numbers like 1.9, 9.902, 15.2, etc. It is accurate upto 15 decimal points.
3. Complex - A complex number contains an ordered pair, i.e., x + iy where x and y denote the real and imaginary parts, respectively. The complex numbers like 2.14j, 2.0 + 2.3j, etc.

10. What is Sequence Type in data type?

String

The string can be defined as the sequence of characters represented in the quotation marks. In Python, we can use single, double, or triple quotes to define a string.

String handling in Python is a straightforward task since Python provides built-in functions and operators to perform operations in the string.

In the case of string handling, the operator + is used to concatenate two strings as the operation "hello"+" python" returns "hello python".

The operator * is known as a repetition operator as the operation "Python" *2 returns 'Python Python'.

The following example illustrates the string in Python.

Example - 1

1. Str = "string using double quotes"  
2. Print(str)  
3. s = '''''A multiline 
4. String'''  
5. Print(s)  

Output:

String using double quotes

A multiline

String

Consider the following example of string handling.

Example - 2

1. Str1 = 'hello javatpoint' #string str1    
2. Str2 = ' how are you' #string str2    
3. Print (str1[0:2]) #printing first two character using slice operator    
4. Print (str1[4]) #printing 4th character of the string    
5. Print (str1*2) #printing the string twice    
6. Print (str1 + str2) #printing the concatenation of str1 and str2    

Output:

He

o

Hellojavatpointhellojavatpoint

Hellojavatpoint how are you