Bending and torsion
Unit-5
Question Bank
Question 1) Explain difference between shear stress and shear strain?
Answer 1)
Shear Diagram | Moment Diagram |
|
M = ∫ V dx |
Question 2)A moment of 1000 Nm is acting on a solid cylinder shaft with diameter 50 mm (0.05 m) and length 1 m. The shaft is made in steel with modulus of rigidity 79 GPa (79 109 Pa).
Answer 2)
Maximum shear stress can be calculated as
τmax = T r / J
= T (D / 2) / (π D4 / 32)
= (1000 Nm) ((0.05 m) / 2) / (π (0.05 m)4 / 32)
= 40764331 Pa
= 40.8 MPa
The angular deflection of the shaft can be calculated as
θ = L T / (J G)
= L T / ((π D4 / 32) G)
= (1 m) (1000 Nm) / ((π (0.05 m)4 / 32) (79 109 Pa))
= 0.021 (radians)
= 1.2 o
Question 3) A moment of 1000 Nm is acting on a hollow cylinder shaft with outer diameter 50 mm (0.05 m), inner diameter 30 mm (0.03 m) and length 1 m. The shaft is made in steel with modulus of rigidity 79 GPa (79 109 Pa).
Answer 3)
Maximum shear stress can be calculated as
τmax = T r / J
= T (D / 2) / (π (D4 - d4) / 32)
= (1000 Nm) ((0.05 m) / 2) / (π ((0.05 m)4 - (0.03 m)4) / 32)
= 46.8 MPa
The angular deflection of the shaft can be calculated as
θ = L T / (J G)
= L T / ((π D4 / 32) G)
= (1 m) (1000 Nm) / ((π ((0.05 m)4 - (0.03 m)4) / 32) (79 109 Pa))
= 0.023 radian)
= 1.4 o
Question 4)A 15 kW electric motor shall be used to transmit power through a connected solid shaft. The motor and the shaft rotates with 2000 rpm. The maximum allowable shear stress - τmax - in the shaft is 100 MPa.
Answer 4)
The connection between power and torque can be expressed
P = 0.105 nrpm T (7)
Where
P = power (W)
nrpm = speed of shaft (rpm)
Re-arranged and with values - the torque can be calculated
T = (15 103 W) / (0.105 (2000 rpm))
= 71 Nm
Minimum diameter of the shaft can be calculated with eq. 4
D = 1.72 ((71 Nm) / (100 106 Pa))1/3
= 0.0153 m
= 15.3 mm
Question 5)Write Assumptions of beams?
Answer 5)
The constraints put on the geometry would form the assumptions:
1. Beam is initially straight and has a constant cross-section.
2. Beam is made of homogeneous material and the beam has a longitudinal plane of symmetry.
3. Resultant of the applied loads lies in the plane of symmetry.
4. The geometry of the overall member is such that bending not buckling is the primary cause of failure.
5. Elastic limit is nowhere exceeded and ‘E' is same in tension and compression.
6. Plane cross - sections remains plane before and after bending.
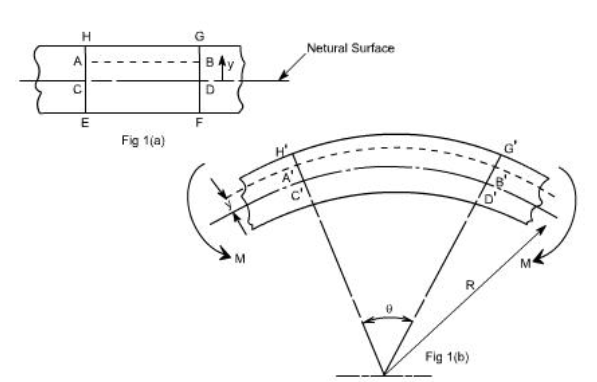
Question 6) A solid shaft of circular in section is subjected to torque which produces maximum shear stress in a shaft. Calculate the diameter of the shaft.?
Answer 6)
Explanation: From torsional equation
T/J = f/R
T = f.Z
T = f×π/16d3.
D= (16T/πf) 3/2
Question 7) Difference between torque and momentum?
Answer 7) Torque vs. Moment:
Torque is force applied at a distance that causes a change in angular momentum. A moment is also a force applied at a distance, but it does not cause a change in angular momentum. In other words, torque causes a body to rotate about an axis, whereas a moment load does not cause rotation.
Question 8) Shear Stress in the Shaft?
Answer 8)
When a shaft is subjected to a torque or twisting a shearing stress is produced in the shaft. The shear stress varies from zero in the axis to a maximum at the outside surface of the shaft.
The shear stress in a solid circular shaft in a given position can be expressed as:
τ = T r / J (1)
Where
τ = shear stress (Pa, lbf/ft2 (psf))
T = twisting moment (Nm, lbf ft)
r = distance from centre to stressed surface in the given position (m, ft)
J = Polar Moment of Inertia of Area (m4, ft4)
Question 9)Explain Circular Shaft and Maximum Moment or Torque?
Answer 9)
Maximum moment in a circular shaft can be expressed as:
Tmax = τmax J / R
Where
Tmax = maximum twisting torque (Nm, lbf ft)
τmax = maximum shear stress (Pa, lbf/ft2)
R = radius of shaft (m, ft)
Combining (2) and (3) for a solid shaft
Tmax = (π / 16) τmax D3
Combining (2) and (3b) for a hollow shaft
Tmax = (π / 16) τmax (D4 - d4) / D
Question 10) Circular Shaft and Polar Moment of Inertia?
Answer 10)
Polar Moment of Inertia of a circular solid shaft can be expressed as
J = π R4 / 2
= π (D / 2)4 / 2
= π D4 / 32 (3)
Where
D = shaft outside diameter (m, in)
Polar Moment of Inertia of a circular hollow shaft can be expressed as
J = π (D4 - d4) / 32 (3b)
Where
d = shaft inside diameter (m, ft)
Diameter of a Solid Shaft
Bending and torsion
Unit-5
Question Bank
Question 1) Explain difference between shear stress and shear strain?
Answer 1)
Shear Diagram | Moment Diagram |
|
M = ∫ V dx |
Question 2)A moment of 1000 Nm is acting on a solid cylinder shaft with diameter 50 mm (0.05 m) and length 1 m. The shaft is made in steel with modulus of rigidity 79 GPa (79 109 Pa).
Answer 2)
Maximum shear stress can be calculated as
τmax = T r / J
= T (D / 2) / (π D4 / 32)
= (1000 Nm) ((0.05 m) / 2) / (π (0.05 m)4 / 32)
= 40764331 Pa
= 40.8 MPa
The angular deflection of the shaft can be calculated as
θ = L T / (J G)
= L T / ((π D4 / 32) G)
= (1 m) (1000 Nm) / ((π (0.05 m)4 / 32) (79 109 Pa))
= 0.021 (radians)
= 1.2 o
Question 3) A moment of 1000 Nm is acting on a hollow cylinder shaft with outer diameter 50 mm (0.05 m), inner diameter 30 mm (0.03 m) and length 1 m. The shaft is made in steel with modulus of rigidity 79 GPa (79 109 Pa).
Answer 3)
Maximum shear stress can be calculated as
τmax = T r / J
= T (D / 2) / (π (D4 - d4) / 32)
= (1000 Nm) ((0.05 m) / 2) / (π ((0.05 m)4 - (0.03 m)4) / 32)
= 46.8 MPa
The angular deflection of the shaft can be calculated as
θ = L T / (J G)
= L T / ((π D4 / 32) G)
= (1 m) (1000 Nm) / ((π ((0.05 m)4 - (0.03 m)4) / 32) (79 109 Pa))
= 0.023 radian)
= 1.4 o
Question 4)A 15 kW electric motor shall be used to transmit power through a connected solid shaft. The motor and the shaft rotates with 2000 rpm. The maximum allowable shear stress - τmax - in the shaft is 100 MPa.
Answer 4)
The connection between power and torque can be expressed
P = 0.105 nrpm T (7)
Where
P = power (W)
nrpm = speed of shaft (rpm)
Re-arranged and with values - the torque can be calculated
T = (15 103 W) / (0.105 (2000 rpm))
= 71 Nm
Minimum diameter of the shaft can be calculated with eq. 4
D = 1.72 ((71 Nm) / (100 106 Pa))1/3
= 0.0153 m
= 15.3 mm
Question 5)Write Assumptions of beams?
Answer 5)
The constraints put on the geometry would form the assumptions:
1. Beam is initially straight and has a constant cross-section.
2. Beam is made of homogeneous material and the beam has a longitudinal plane of symmetry.
3. Resultant of the applied loads lies in the plane of symmetry.
4. The geometry of the overall member is such that bending not buckling is the primary cause of failure.
5. Elastic limit is nowhere exceeded and ‘E' is same in tension and compression.
6. Plane cross - sections remains plane before and after bending.
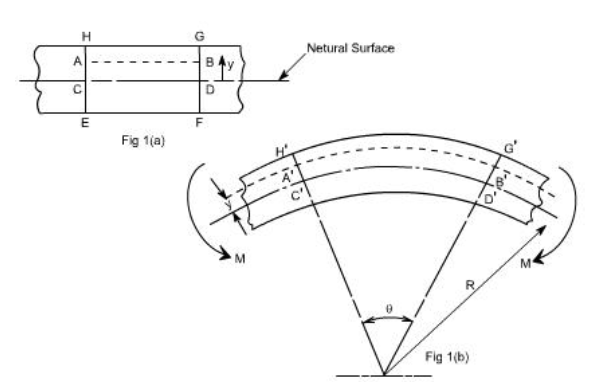
Question 6) A solid shaft of circular in section is subjected to torque which produces maximum shear stress in a shaft. Calculate the diameter of the shaft.?
Answer 6)
Explanation: From torsional equation
T/J = f/R
T = f.Z
T = f×π/16d3.
D= (16T/πf) 3/2
Question 7) Difference between torque and momentum?
Answer 7) Torque vs. Moment:
Torque is force applied at a distance that causes a change in angular momentum. A moment is also a force applied at a distance, but it does not cause a change in angular momentum. In other words, torque causes a body to rotate about an axis, whereas a moment load does not cause rotation.
Question 8) Shear Stress in the Shaft?
Answer 8)
When a shaft is subjected to a torque or twisting a shearing stress is produced in the shaft. The shear stress varies from zero in the axis to a maximum at the outside surface of the shaft.
The shear stress in a solid circular shaft in a given position can be expressed as:
τ = T r / J (1)
Where
τ = shear stress (Pa, lbf/ft2 (psf))
T = twisting moment (Nm, lbf ft)
r = distance from centre to stressed surface in the given position (m, ft)
J = Polar Moment of Inertia of Area (m4, ft4)
Question 9)Explain Circular Shaft and Maximum Moment or Torque?
Answer 9)
Maximum moment in a circular shaft can be expressed as:
Tmax = τmax J / R
Where
Tmax = maximum twisting torque (Nm, lbf ft)
τmax = maximum shear stress (Pa, lbf/ft2)
R = radius of shaft (m, ft)
Combining (2) and (3) for a solid shaft
Tmax = (π / 16) τmax D3
Combining (2) and (3b) for a hollow shaft
Tmax = (π / 16) τmax (D4 - d4) / D
Question 10) Circular Shaft and Polar Moment of Inertia?
Answer 10)
Polar Moment of Inertia of a circular solid shaft can be expressed as
J = π R4 / 2
= π (D / 2)4 / 2
= π D4 / 32 (3)
Where
D = shaft outside diameter (m, in)
Polar Moment of Inertia of a circular hollow shaft can be expressed as
J = π (D4 - d4) / 32 (3b)
Where
d = shaft inside diameter (m, ft)
Diameter of a Solid Shaft