Question Bank
UNIT -1
Question Bank
UNIT -1
FUNCTIONS OF ONE VARIABLE
Q 1:
Find the nth derivative of sin3 x
Solution:
We know that sin 3x= 3sin x 4sin3 x = sin3x = 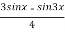
Differentiate n times w.r.t x,
dn/dxn ( sin3 x) = 1/4 dn/dxn (3 sinx- sin3x)
=1/4 ( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
Q 2:
Find the nth derivative of sin 5x. Sin 3x.?
Sol: let y = sin 5x.sin 3x= 1/ 2( sin 5x.sin 3x)
⇒y= ½( cos 2x - cos8x)
⇒ y= ½ ( cos 2x- cos8x )
Differentiate n times w.r.t x,
Yn = ½ (dn/dxn) ( cos 2x - cos8x )
⇒ yn = ½ ( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
Successive n th derivative of nth elementary function ie., exponential
If y = ae n x + be –nx , then show that y2= n2y
Sol: Y= aenx + be-nx
y 1 = a.n.enx - b.n.e-nx
y2 = an2 enx – bn2 e-nx = n2 (ae nx+ be –nx)
y2= n2y.
Q 3:
If y= e-kx/2(a cosnx+ b sinnx) then show that.,y2+ ky1+(n2+ k2/4)y =0
Sol : y= e-kx/2(a cosnx+ b sinnx)
Differentiating w.r.to. x.,
 Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y

 Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx) (1)
Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx) (1)
Differentiating w.r.to x.,
Y2+ k/2.y1 = ne-kx/2 (-k/2) ( -an sin nx + bn cos nx) + n e-kx/2(-an cosnx- bn sinnx).
= -(k/2) (y1+ k/2 y)- n2 y = - (k/2 y1)- ( k2/4)y- n2y.
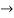 y2 + ky1 +(n2+ k2/4)y = 0.
y2 + ky1 +(n2+ k2/4)y = 0.
Successive differentiation of nth derivative of elementary functions ie., logarithmic
Q 4:
If Y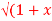 2) = log( x +
2) = log( x + 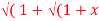 2) ) then show that (1 + x 2) y1 +xy =1
2) ) then show that (1 + x 2) y1 +xy =1
Sol: Y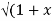 2) = log( x +
2) = log( x +  2) )
2) )
Differentiating w.r.to x.,
y.1/ 2 2 .2x+
2 .2x+ 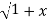 2. Y1.
2. Y1.
=(1+x ) y +xy =  . 1/x+
. 1/x+ 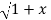 2 .
2 . 2) +x/
2) +x/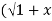 2 =1
2 =1
Q5:

Solution:
It is an alternating series ,with
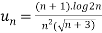 here (-1)n defines only the sign
here (-1)n defines only the sign
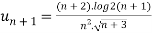
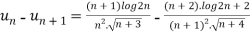
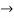
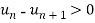 for all n
for all n

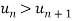
Now,
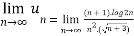
=
=0 as 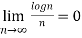
Hence by Leibnitz’s rule of alternating series 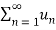 is converging.
is converging.
Q 6:
Q = 9R2-  to find
to find 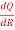
Solution:
Q = 9R2-15R-3
Now,
 = 18R+45R-2 = 18R +
= 18R+45R-2 = 18R +
Power series:
A power series can be written in the form of

It can be written in the form of a function as.,
f(x) =
If we let 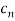 =1 for all n then the power series tends to geometric series
=1 for all n then the power series tends to geometric series
f(x) = 1+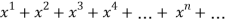
The above series converges if -1<x<1
The above series diverges if x≥ 1 and x
Q 7:
 n
n
L= 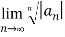 =
= 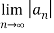 1/n
1/n
L= 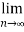
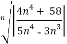 n =
n =
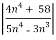
=  <1
<1
Hence the series converges.
Q 8:
Use lagranges mean value thorem to determnine a point P on the curve y=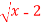 ,where the tangent is parallel to the chord joining (2,0) and (3,1).
,where the tangent is parallel to the chord joining (2,0) and (3,1).
Solution:
Consider y=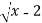 in [2,3]....(1)
in [2,3]....(1)
(i)Function is continuous in[2,3] as algebraic expression with positive exponent is continuous
(ii)y’= ,y’ exists in (2,3) hence the function is derivable in(2,3)
,y’ exists in (2,3) hence the function is derivable in(2,3)
Hence the conditions of LMV theorem are satisfied.
Hence thereexists, at least one c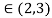 ,such that
,such that 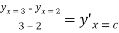
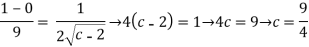
 For x=
For x= ,tangent is parallel to the chor joining(2,0) and (3,1)
,tangent is parallel to the chor joining(2,0) and (3,1)
By substituting in equation (1) we get ,
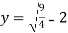 =
=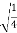 =
= 
Q 9:
Find the slope point on the graph y=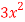 on[1,2] at which the tangent to the graph has the same slope as the line that passes through the end points (1,2) and (3,12)of the closed interval.
on[1,2] at which the tangent to the graph has the same slope as the line that passes through the end points (1,2) and (3,12)of the closed interval.
Solution:
Step 1: find the slope of the points that passes through the endpoints at

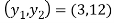
 the required slope is given by
the required slope is given by  =
=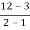 =9
=9
Step 2:
Find the point on the curve where the slope is 9
Y’=6x
6x=9 
 the instantaneous rate of change of slope is 9
the instantaneous rate of change of slope is 9
Q 10:
Show that sinx<x for all x>0
Solution:
If x>2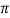 ,then sinx
,then sinx 1<2
1<2 <x. If 0<x
<x. If 0<x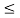 2
2 ,then by the mean value theorem,there-exists c in open interval(0,2
,then by the mean value theorem,there-exists c in open interval(0,2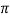 ) such that
) such that
 x=c = cosc<1
x=c = cosc<1
Thus, sinx<x in this case also.
Q 11:
Find the values of the c,which satisfy the equation 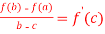 as stated in mean value theorem for the function f(x) =
as stated in mean value theorem for the function f(x) = in the interval [1,3]
in the interval [1,3]
Solution:
First let us check the mean value theorem conditions,
F(x) is continuous in its domain[0, and hence the given interval [1,3]
and hence the given interval [1,3]
F(x) is also differentiable in the given interval .plugging a=1 and b=3 in the expression on the left side of the equation.
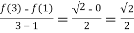
Now, the derivative of the function can be found using chain rule as
f’(x) =
Hence, the equation can be formed as
f’(c)= 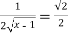
Cross multiplying and squaring the equation reduces to,
2(c-1)=1 which gives the solution as c=3/2 which lies in the interval [1,3].
Q 12:
In a geometric progression,the second term is 12 and the sixth term is 192.find the eleventh term
Solution:
The required geometric progression is,
a+ar+ar2+ar3+.....
Given the second term is ar=12...(1)
Sixth term is ar5 = 192.....(2)
Dividing eq(2) by eq(1) we get ,

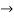 r4 = 16
r4 = 16
Substituting r in eq(1) we get ar=12/2=6
 eleventh term is given by ar10 = 6
eleventh term is given by ar10 = 6 210 =6144
210 =6144
Q 13:
If sn denotes the sum of first n terms of an A.P and [s3n-sn-1]/[s2n-s2n-1]=31,then the value of n is
Solution:
S 3n = [3n / 2] [2a + (3n − 1) d]
Sn−1 = ([n − 1] / 2) * [2a + (n − 2) d]
⇒ S3n − Sn−1 = [1 / 2] [2a (3n − n + 1)] + [d / 2] [3n (3n − 1) − (n − 1) (n − 2)]
= [1 / 2] [2a (2n + 1) + d (8n2 − 2)]
= a (2n + 1) + d (4n2 − 1)
= (2n + 1) [a + (2n − 1) d]
S2n − S2n−1 = T2n = a +(2n − 1) d
⇒ S3n − Sn − S2n −S2n−1 = (2n + 1)
Given, ⇒ [S3n − Sn−1] / [S2n − S2n−1] = 31
⇒ n = 15
Q 14:
If Sn denotes the sum of first n terms of an A.P ,whose first term is  is independent of x,then SP =?
is independent of x,then SP =?
Solution:
 =
= 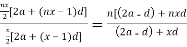
For 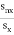 to be independent
to be independent
2a-d=0 or 2a=d
Now,
Sp = 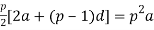
Q 15:
Find the taylor series for the following:

 =
= 
 <1
<1
 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
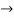 ROC =10
ROC =10
Q 16:
f(n)5 = 
Here the ROC is 4
Q 17:
f(x)=

= f(0)+f’(0)x+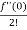 x2 +
x2 + 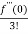 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 
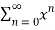
Q 18:
Solve the following improper integral  dx
dx
Solution:
By definition
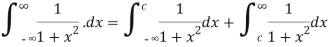
Here we consider at c=0
 =
= 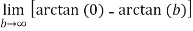
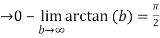
Here the integral converges at 
Q 19:
Find 
Solution:
The denominator of 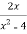 is 0 when x=2, so the function is not defined even when x=2.so,
is 0 when x=2, so the function is not defined even when x=2.so,
 =
=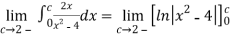
 -ln(4) =-
-ln(4) =-
So the integral diverges