HARCOURT BUTLER TECHNICAL UNIVERSITY

UNIT-5

STATISTICAL MECHANICS & LASERS

QUESTION BANK

1 Question: Derive expression for the probability of distribution & what is the most and least probable distribution?

Solution:

Microscopic and Macroscopic Systems

Let us consider a gas confined in a container. It is the collection of very large number of molecules or atoms of the order of 1020 or higher. A gas molecule or atom in a container is a microscopic system whereas the gas in the container is a macroscopic system. The detailed specification of the microscopic state or microstate of any system of N particles involves specifying the positions and velocities (in classical approach) of all the N particles and specifying wave functions of all N particles (in quantum approach). The number of particles N is so large that to write the microstate of a mole of a gas it will require more than India’s total supply of paper, making it practically impossible. Fortunately, in statistical mechanics it is not attempted either. Rather, we want to know just a small number of macroscopic variables that are statistical averages over the many microscopic variables. For example, to specify the macroscopic state or macrostate, of a gas confined in a container, we need only to give the volume V, the number of atoms N, the total energy E and the temperature T.

Accessible and Inaccessible States

The microstate/macrostates which are allowed under given constraints are called accessible states. For example, let us distribute four particles between two halves of a box, then the possible arrangements or macrostates are (4 0), (3. 1), (2, 2), (1, .3) and (0, 4). Hence the accessible macrostates are five. On the other hand, microstates/macrostates which are not allowed under given constraints are called inaccessible states. For example, macrostate (l, 2) and (3, 2) in the above example are inaccessible macrostates. Thus, constraints on the system determines the number of accessible and inaccessible microstate/macrostates,

Distribution of N Particles In Two Compartments

Consider n distinguishable particles to be distributed in two compartments of equal size of a box. Let us assume that there is no restriction on the number of particles that can enter into either of the compartment. We know, the number of macrostates is one more than the number of particles to be arranged.

Hence, in this case, the number of macrostates = (n + 1)

These macrostates arc (0,n), (1, n -1), (2, n - 2)......(n,0).

The number of microstates (i.e. arrangements) can be calculated as follows:

The first particle can be put in two ways i.e., either in the first or in the second compartment. Similarly, the second particle can also he put in two ways in two compartments. Therefore, the total number of ways in which two particles can be put in two compartments is four i.e. 2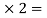 22.

Similarly, the total number of ways (arrangements) in which n particles can be distributed in two compartments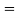 22 = number of microstates.

Now, n particles can be arranged themselves in nPn, for [P (n, n)]= 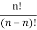= 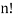ways

These 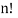ways include meaningful as well as meaningless ways.

Total number of ways (n!) = No. Of meaningful arrangements x No. Of meaningless arrangements                                                                                                                               ……....(1)

Suppose we have four particles and three out of them are in the first compartment and one in the second compartment. Now this distribution gives one macrostate. These three particles in the first compartment can be arranged in six ways. These arrangements are meaningless, as they are simple repetitions. Therefore, three particles has 6 = 3 x 2 x 1 = 3 ! Meaningless arrangements.

If we have n1, particles in one compartment and n2 in the second compartment, then the meaningless in compartment 1 and 2 respectively are n1! and n2!.

In other words, total meaningless arrangements are n1!n2!.

Hence eqn. (1) becomes

n! = Number of meaningful arrangements n1!n2!

Number of meaningful arrangements = 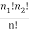……....(2)

Now, the number of meaningful microstates in a given macrostate is equal to the number of microstates in a given macrostate is called Thermodynamic probability (W).

Thermodynamic probability of the given macrostates (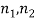) is given by by eqn (2)

W (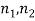) = = 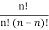   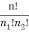 [n =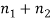 ]……....(3)

We know, the probability of a  macrostates is equal to the ratio of the number of microstates in it to the total number of microstates in the system.

P () =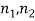

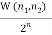
Using equation (3)

P () = =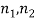

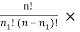
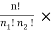
The probability distribution of (r, n-r) is given by

P () =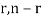

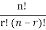
Combination Possessing Maximum Probability

Suppose we have n similar coins and they are tossed many times. We know, the value of "Cr is maximum when r = n/2 (where n is even). Hence the maximum probability is given by

Pmax =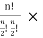

The combination having maximum probability is known as most probable combination.

Combination Possessing Minimum Probability

We know, "Cr is minimum when r = 0 or r = n Hence, minimum probability is given by

Pmin = =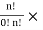

The combination having minimum probability is known as least probable combination.

2 Question: Discuss Maxwell-Boltzmann Statistics ?

Solution:

Maxwell-Boltzmann Statistics

The basic postulates of MB statistics are:-

(i)The associated particles are distinguishable.

(ii)Each energy state can contain any number of particles.

(iii)Total number of particles in the entire system is constant.

(iv)Total energy of all the particles in the entire system is constant.

(v)Particles are spinless.

Examples: gas molecules at high temperature and low pressure.

One of the general ideas contained in these postulates is that it is unlikely that any one particle will get energy far above the average (i.e., far more than its share). Energies lower than the average is favoured because there are more ways to get them. If one particle gets energy of 10 times the average, for example, then it reduces the number of possibilities for the distribution of the remainder of the energy. Therefore it is unlikely because the probability of occupying a given state is proportional to the number of ways it can be obtained.

Maxwell-Boltzmann Distribution Law

Consider a system composed of N distinguishable, non-interacting particles. Let out of these N particles N1, N2,.....,Ni particles are to be distributed in energy levels E1,E2,....,Ei respectively and these energy levels have g1,g2,......,gi number of quantum states correspondingly. Since the total energy E and total number of particles N are constant for the system, we can write

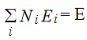………..(1)

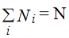………..(2)

The number of ways in which the groups of particles N1, N2,....., Ni could be chosen from N particles is

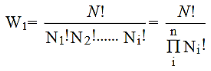………..(3)

Where  denotes the product. Now, Ni particles can be distributed in gi states in 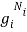ways. Considering all the values of i, total number of arrangement would be

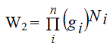………..(4)

Therefore, the total number of ways W by which all the N particles could be distributed among the quantum states is

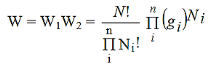………..(5)

This is the Maxwell-Boltzmann distribution law for n distinguishable particles.

Now taking the natural logarithm on both sides of equation (5), we get

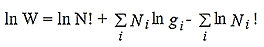………..(6)

Applying Stirling approximation (i.e.,lnx! = x ln x –x, where x is very large), we get from equation (7)

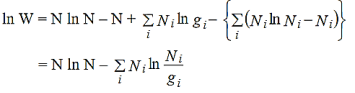
………..(7)

Now differentiating both sides we get,

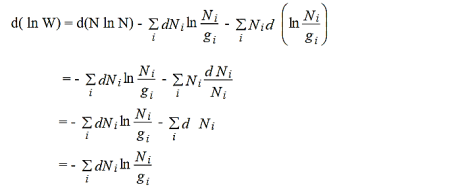………..(8)

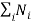  constant = 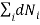= 0

For the most probable distribution, d( ln W)max= 0

Therefore

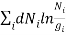= 0………..(9)

Since the system is in equilibrium, total number of particle and the total energy of the system are constant. So,

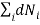  0 ………..(10)

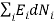 0………..(11)

Multiplying equation (10) by α and equation (11) by β and then adding to equation (9), we get,

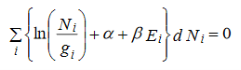………..(12)

Since dNi’s are independent of one another, the above equation holds only if

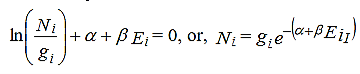………..(13)

Now the Maxwell-Boltzmann distribution function is given by

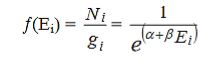………..(14)

Which physically gives the probability of a particle to occupy the energy state Ei.

Boltzmann distribution gives the fundamental understanding of classical molecular phenomena, which tells us that the probability that any one molecule will be found with energy E decreases exponentially with energy; i.e., any one molecule is highly unlikely to grab much more than its average share of the total energy available to all the molecules. Mathematically, the Boltzmann distribution can be written in the form

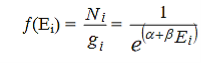
This distribution can be made believable by a numerical example, particularly when put in graphical form, but the rigorous mathematical development by Boltzmann still stands as a major achievement in the mathematics of physics. This distribution gives a postulate in the development of physical models in kinetic theory.

This idea that each "particle" is unlikely to have much more or less than its "fair share" of the energy can be extended to "modes" in wave phenomena such as the electromagnetic wave modes in a cavity, although this application shows its classical limitations in the Rayleigh-Jeans law.

Another idea contained in the Boltzmann distribution above is that if the general "energy economy" is improved by increasing the temperature so that the total energy available to the particles is increased, a given particle is more likely to get a specified amount of energy. If the overall financial economy of the country is better with more money in circulation, then for any particular financial threshold you picked, there would be a higher probability that any given individual would reach that threshold. By analogy, if there is some particular threshold energy for a given phenomenon, such as ionization or excitation of vibrational states, then the likelihood of that phenomenon happening will increase with temperature in a generally predictable way.

3 Question: Discuss Bose-Einstein Distribution Law?

Solution:

The basic postulates of BE statistics are:-

(i)  The associated particles are identical and indistinguishable.

(ii) Each energy state can contain any number of particles.

(iii) Total energy and total number of particles of the entire system is constant

(iv) The particles have zero or integral spin, i.e. 0ℏ, 1 ℏ, 5 ℏ, 50 ℏ etc, where ℏ is the unit of spin.

(v) The wavefunction of the system is symmetric under the positional exchange of any two particles. Examples: photon, phonon, all mesons (,,) etc., these are known as Bosons.

Symmetric and Anti-symmetric wave function

Suppose the allowed wave function for a n-particles system is ψ(1,2,3,.....,r, s,...n), where the integers within the argument of ψ represent the coordinates of the n-particles relative to some fixed origin. Now, if we interchange the positions of any two particles, say, r and s, the resulting wave function becomes ψ(1,2,3,....s, r,.....n). The wave function ψ is said to be symmetric when

ψ(1,2,3,.....,r,s,...n) = ψ(1,2,3,....s,r,.....n)

And Anti-symmetric when

ψ(1,2,3,.....,r,s,...n) = - ψ(1,2,3,....s,r,.....n)]

Bose-Einstein Distribution Law:

Let Ni number of identical, indistinguishable, non-interacting particles are to be distributed among gi quantum states each having energy Ei. So, in the ith energy level, there are (Ni+gi) total objects. Keeping the first quantum state fixed, the remaining (Ni+ gi-1) objects can permuted in (Ni+ gi-1)! possible ways. But since the particles and the quantum states are indistinguishable, we have to deduct Ni! ways and (gi–1)! ways from the all possible ways to get effective number of arrangements. Thus total number of possible ways of arrangement for the ith state is

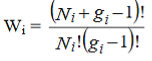……….(1)

Hence the total number of ways of the entire distribution of N particles in n number of energy levels of the system is

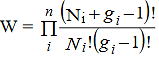……….(2)

Where  denotes the product symbol. If we assume that Ni and gi are very large, equation (2) reduces to             

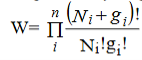……….(3)

Taking natural logarithm of both the sides of equation (3) we get,

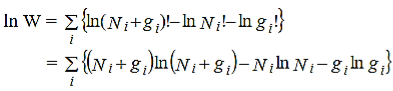……….(4)

Using Stirling approximation, Now, differentiating equation (4) to obtain the most probable distribution, we get,

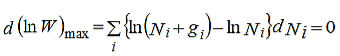
Also we have other two conditions given by

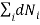 0 (conservation of total no of particles)………..(5)

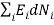 0(conservation of total energy)       ………..(6)

Multiplying equation (5) by (-α) and equation (6 ) by (-β) and then adding with equation (4 ) we get,

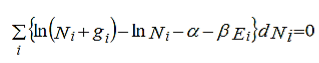………..(7)

Since dNi’s are independent of one another, the above equation holds only if,

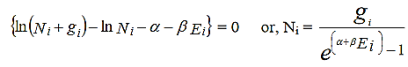………..(8)

Now the Bose-Einstein distribution function is given by

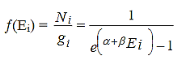………..(9)

Which represents the probability of finding a boson with energy Ei.

4 Question: Discuss FD statistics?

Solution:

The basic postulates of FD statistics are:-

(i)Particles are identical and indistinguishable.

(ii)Total energy and total number of particles of the entire system is constant (iii)Particles have half-integral spin, i.e. etc, , , .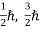

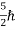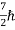(iv)Particles obey Pauli’s exclusion principle, i.e. no two particles in a single system can have the same value for each of the four quantum numbers. In other words, a single energy state can contain at best a single particle with appropriate spin.

(v) The wave function of the system is anti-symmetric under the positional exchange of any two particles.

Examples: electron, proton, neutron, all hyperons (Λ, Σ, Ξ, Ω) etc., these are known as Fermions.

Fermi-Dirac Distribution Law:

Consider a system of N indistinguishable, non-interacting particles obeying Pauli’s exclusion principle. Let N1, N2, N3, ....Ni,....Nn Particles in the system have energies E1, E2, E3, ....,Ei,...En respectively and let gi is the number of degenerate quantum states in the energy level Ei. According to Pauli’s exclusion principle a single quantum state can be occupied by at best one particle. Since Ni particles are to be distributed among gi degenerate states (gi ≥Ni) having the same energy Ei, Ni states will be filled up and (gi -Ni) states will remain vacant. Now gi states can be arranged in gi! possible ways. But since the particles and the quantum states are indistinguishable, we have to deduct Ni! ways and (gi -Ni)! ways from the all possible ways to get effective number of arrangements. Thus total number of possible ways of arrangement for the ith state is

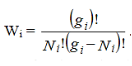…………(1)

Hence the total number of ways for the entire distribution of N particles in n number of energy levels of the system is

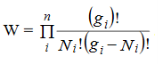…………(2)

Where  denotes the product symbol. Now taking natural logarithm on both sides of equation (2) and applying Stirling approximation, we get,

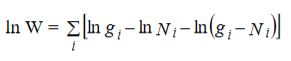…………(3)

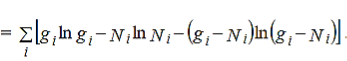…………(4)

Now, differentiating equation (4) to obtain the most probable distribution, we get,

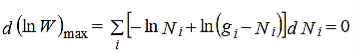…………(5)

Considering the conservation of total energy and total number of particles, we can write

Also we have other two conditions given by

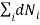 0 (conservation of total no of particles)………..(6)

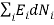 0(conservation of total energy)       ………..(7)

Multiplying equation (6) by (-α) and equation (7) by (-β) and then adding with equation (5) we get,

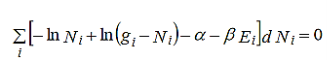       ………..(8)

Since dNi’s are independent of one another, the expression in the bracket of equation (8) is zero for each Ni. Thus

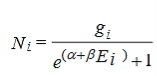………..(9)

Hence the Fermi-Dirac distribution function is given by

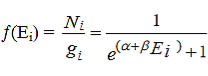………..(10)

Which represents the probability of finding a fermion with energy Ei.

5 Question: What is the effect of temperature on Fermi Function Discuss FD statistics?

Solution:

Fermi function F (E):

Fermi-Dirac distribution function represents the probability of an electron occupying a given energy level at absolute temperature. It is given by

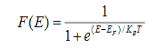
Where KB Boltzmann Constant

T Temperature

If g(E) is the density of states and f(E) gives the probability of occupation of those states at a given temperature, the number of occupied states, n(E),is given by

n(E) = 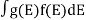(1)

If the number of occupied states in an energy band needs to be calculated the integration needs to be performed over the entire band. This will be a function of temperature, since the Fermi function is temperature dependent. Equation 1 can be used to calculate the concentration of electron and holes in semiconductors, which decides their conductivity.

Effect of temperature on Fermi Function:

Case (i) Probability of occupation for E < EF at T = 0K

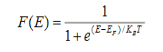
When T = 0K and E < EF, we have

F(E) = 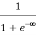=  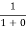= 1

Thus at T = 0K, there is 100 % chance for the electrons to occupy the energy levels below the Fermi level.

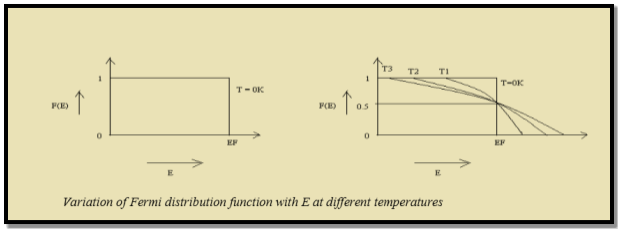
Figure 6: Fermi distribution

Case (ii) Probability of occupation for E>EF at T = 0K

When T = 0K and E > EF, we have

F(E) = 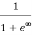=  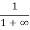= = 0

Thus, there is 0 % chance for the electrons to occupy energy levels above the Fermi energy level. From the above two cases, at T = 0K the variation of F(E) for different energy values becomes a step function.

Case (iii) Probability of occupation at ordinary temperature

At ordinary temperature, the value of probability starts reducing from 1 for values of E slightly less than EF. With the increase of temperature, i.e., T> 0K, Fermi function F (E) varies with E.

At any temperature other than 0K and E = EF

F(E) = 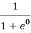=  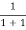= = 50%

Hence, there is 50 % chance for the electrons to occupy Fermi level. Further, for E > EF the probability value falls off rapidly to zero.

Case (iv) At high temperature

When kT >> EF, the electrons lose their quantum mechanical character and Fermi distribution function reduces to classical Boltzmann distribution

6 Question: Derive expression for Fermi energy for electron gas in metals?

Fermi energy for electron gas in metals

Solution:

Metals are characterized by the presence of a good number of free electrons. These electrons move about at random within the metals. While moving the free electrons collide among themselves also encounter with the fixed ion cores. Such behaviour of the free electrons is similar to that of molecules of a gas. Thus metals can be treated as electron gas. Since the electrons have half-integral spin angular momenta and they obey Pauli’s exclusion principle, they follow F-D statistics.

Let us consider an electron gas consisting of N electrons occupying volume V. If N is very large, the spacing between two successive energy levels becomes very small making the energy levels almost continuous. Then if the energy of the electrons ranges between E to E+dE, the number of degenerate states gi should be replaced by g(E)dE and the total number of electrons Ni in these states should be replaced by N(E)dE in the distribution function.

Thus the total number of electrons in the electron gas having energy between E to E+dE can be written by following equation

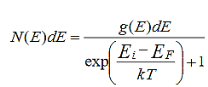………..(1)

Since the electrons have two allowed values of spin quantum number (ms= ± ½), the total number of their allowed states between energy for the energy range E to E+dE can be written as

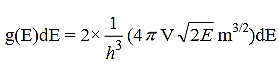………..(2)

Hence the density of states g(E) for a Fermionic gas is given by

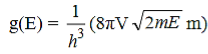………..(3)

Which shows that g(E) depends only on E for a single type of fermionic gas kept in a fixed volume V. From (figure 6)  it is obvious that at T = 0K, all the single-particle states up to energy EF are filled up.

Thus at T = 0K

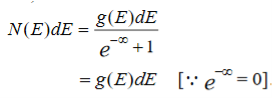………..(4)

i.e., total number of electrons is equal to the total number of single-particle energy states, hence

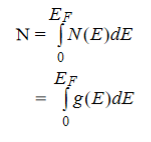………..(5)

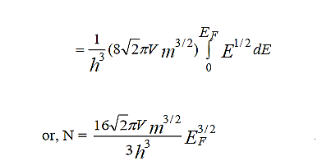………..(6)

Which is the expression for the total number of electrons in the metal at T = 0K.Therefore

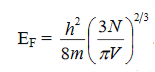………..(7)

Which is the expression for Fermi energy of the electrons in the metal. If n = N/V denotes the concentration of the electrons in the metal, the Fermi energy of the electrons in the metal is

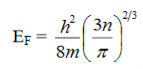………..(8)

Which shows the Fermi energy of the electrons depends solely on their concentration.

Total energy at absolute zero temperature:

The total energy of electrons at absolute zero (T = 0K) is given by

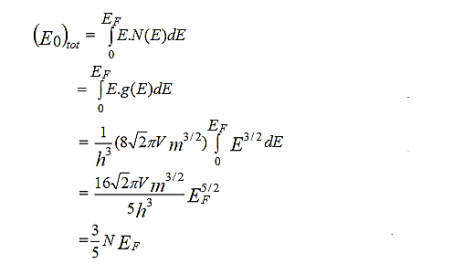………..(9)

Which shows quantum effect because, classically the total energy of a system at absolute zero is nothing but zero. The average energy per electron at T = 0K can be written as

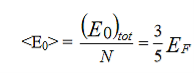…………..(10)

Which shows that at absolute zero temperature, the average energy per electron is equal to 3/5 times the Fermi energy.

The ground-state pressure of the system is defined by

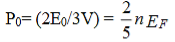…………..(11)

Substituting for EF, the foregoing expression takes the form

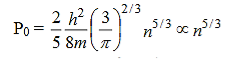…………..(12)

Thus the ground-state pressure of an electron gas at absolute zero solely depends on its concentration.

Fermi Temperature (TF):

Fermi temperature (TF) is the temperature equivalent of Fermi energy (FF) and it is defined as, TF = EF/k where k (= 1.38×10-23Joule/Kelvin) is the Boltzmann constant.

7 Question: Derive expression of average velocity, rms velocity and most probable velocity by using Maxwell-Boltzmann distribution law?

Solution:

The velocity distribution law was derived by Maxwell on the basis of kinetic theory of gases. Suppose n molecules of a gas are contained in a container of volume V. From Maxwell-Boltzmann distribution law, we have

………….(1)

For monoatomic gases, the value of 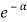is given by

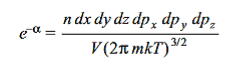………….(2)

Substituting the values of 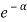and 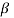in Equation (1), replacing ni the number of molecules in the ith state by dn and omitting the subscription from Ei, we get

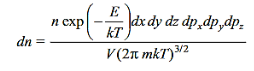………….(3)

Integrating over the coordinates x, y, z (so that 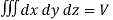), yields

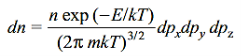………….(4)

Here, dn represents the number of molecules in the container with momentum components in the interval dpx, dpy and dpz. The translational energy E of a molecule having mass m is given by

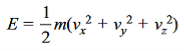………….(5)

While its momentum components can be represented as

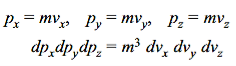………….(6)

Substituting these in Eq. (2.21), we have

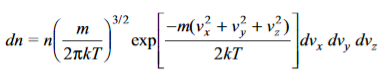………….(7)

This is Maxwell’s distribution law for the number of molecules with velocity components in the interval dvx, dvy and dvz. Writing the velocity components vx, vy and vz in terms of the speed of a molecule v and changing over to polar coordinates, so that

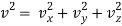………….(8)

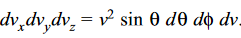………….(9)

Substituting these values in Equation (2.25), we get

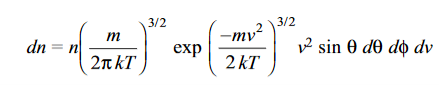………….(10)

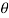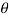This equation gives the number of molecules with speeds between v and v+dv in a direction lying within the angular range to +d 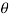and ϕ to ϕ +d ϕ. Integration over the angular part gives the number of molecules with velocity between v and v+dv.

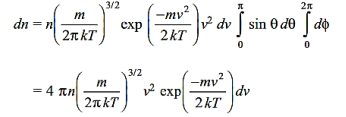………….(11)

Using F(v)dv to denote the number of molecules having speeds between v and v+dv, we have

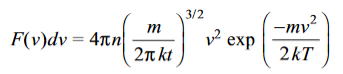………….(12)

The function F(v)dv is called the Maxwell speed distribution function derived by Maxwell before development of quantum mechanics or quantum statistics. The function F(v) is represented in Figure.

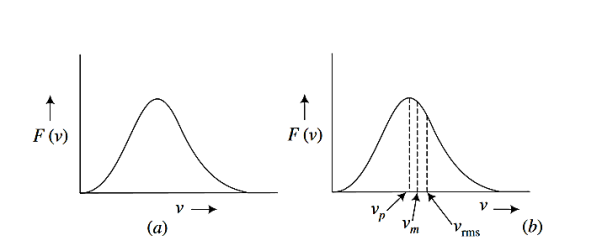
Figure: 1 (a) The Maxwell speed distribution (b) most probable speed (vp), mean speed (vm) and rms speed (vrms) marked on speed distribution.

The Maxwell speed distribution has been experimentally verified. The Maxwell speed distribution for O2 and comparatively lighter H2 molecules are shown in Figure 1 In both the cases there is tail out at higher speeds, but few molecules have speeds higher than about three times the most probable speed, which would correspond to energy nine times the most probable energy. This indicates why there is almost no hydrogen in the earth’s atmosphere. For hydrogen, the tail of the speed distribution extends beyond the earth’s escape speed (~10km/s), so that any hydrogen in the earth atmosphere eventually leaks into the space. Smaller astronomical bodies such as moon and asteroids have such low escape velocities that all gases on their surfaces escape to space.

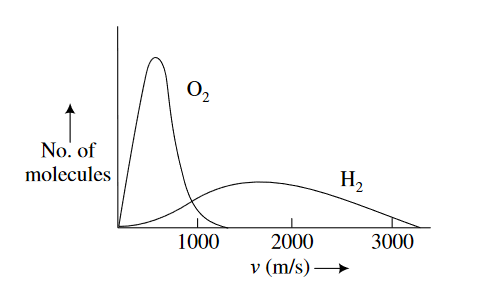
Figure: 2

Since the kinetic energy E = mv2, we can write

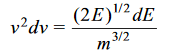………….(13)

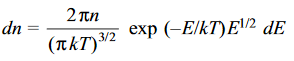………….(14)

Which gives the number of molecules (or atoms) having energy between E and E+dE. The most probable speed vp corresponds to the peak of F(v) versus curve (Figure 1(b)). for F(v) to be maximum

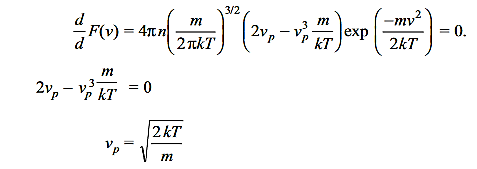
………….(15)

The mean speed vm is calculated as

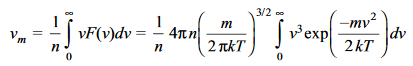………….(16)

Putting the value of the integral

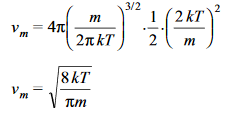………….(17)

The root mean square speed vrms is given by

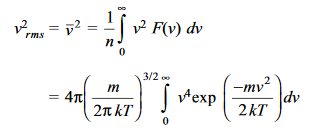
Putting the value of the integral

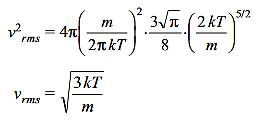………….(18)

The values of vp, vm and vrms are represented in Figure 1 (b).

8 Question: What is black body and black body radiation?  Also explain Emissive power and Absorptive power of a black body?

Solution:

A hot body emits thermal radiations which depend on composition and the temperature of the body. The ability of the body to radiate is closely related to its ability to absorb radiation.

A Body which is capable of absorbing almost all the radiations incident on it is called a black body.

A perfectly black-body can absorb the entire radiations incident on it. Platinum black and Lamp black can absorb almost all the radiations incident on them.

Emissive power of a black body:

It is defined as the total energy radiated per second from the unit surface area of a black body maintained at certain temperature.

Absorptive power of a black body:

It is defined as the ratio of the total energy absorbed by the black body to the amount of radiant energy incident on it in a given time interval. The absorptive power of a perfectly black body is 1.

One of the major ideas of quantum physics is quantization, measuring quantities in discrete, not continuous units.

The problem of black-body radiation one of the earliest challenges to classical physics.

When you heat an object, it begins to glow. Even before the glow is visible, it’s radiating in the infrared spectrum. The reason it glows is that as you heat it, the electrons on the surface of the material are agitated thermally, and electrons being accelerated and decelerated radiate light.

Physics in the late 19th and early 20th centuries was concerned with the spectrum of light being emitted by black bodies. A black body is a piece of material that radiates corresponding to its temperature — but most ordinary objects you think of as black, such as charcoal, also absorb and reflect light from their surroundings.

Well, it was hard to come up with a physical black body after all, what material absorbs light 100% and doesn’t reflect anything? But the physicists were clever about this, and they came up with the hollow cavity with a hole in it.

As discussed the blackbody is an idealization, because no physical object absorbs 100% of incident radiation, we can construct a close realization of a blackbody in the form of a small hole in the wall of a sealed enclosure known as a cavity radiator, as shown in Figure.

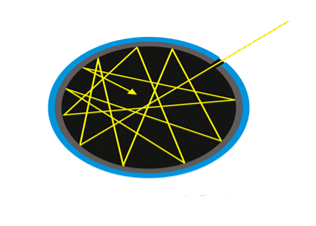
Figure: Black Body

The inside walls of a cavity radiator are rough and blackened so that any radiation that enters through a tiny hole in the cavity wall becomes trapped inside the cavity. At thermodynamic equilibrium (at temperature T), the cavity walls absorb exactly as much radiation as they emit. Furthermore, inside the cavity, the radiation entering the hole is balanced by the radiation leaving it. The emission spectrum of a blackbody can be obtained by analyzing the light radiating from the hole. Electromagnetic waves emitted by a blackbody are called blackbody radiation.

9 Question: Explain Spectral Distribution of energy in thermal radiation?

Or

Explain Black Body radiation spectrum?

Solution:

A good absorber of radiation is also a good emitter. Hence when a black body is heated it emits radiations. In practice a black body can be realized with the emission of Ultraviolet, Visible and infrared wavelengths on heating a body.

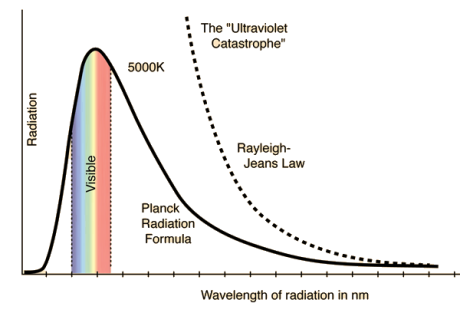
German physicists Lummer and Pringsheim studied the energy density as a function of wavelength for different temperatures of a black body using a spectrograph and a plot is made. This is called Black Body radiation spectrum.

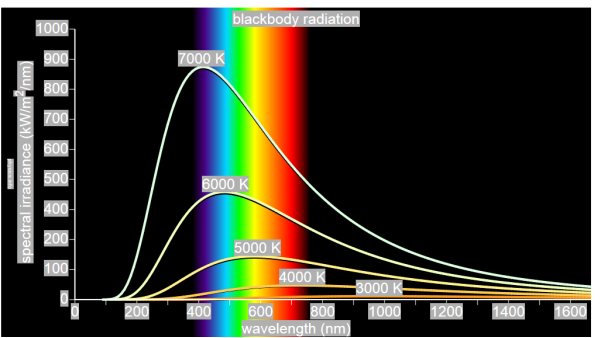
You can see the spectrum of a black body (and attempts to model that spectrum) in the above figure, for different temperatures. One needs simply to analyse the spectral distribution of the radiation coming out of the hole. The radiation emitted by a blackbody when hot is called blackbody radiation.

The intensity I(λ,T) of blackbody radiation depends on the wavelength λ of the emitted radiation and on the temperature T of the blackbody.

The function I(λ,T) is the power intensity that is radiated per unit wavelength.

In other words, it is the power radiated per unit area of the hole in a cavity radiator per unit wavelength. According to this definition, I(λ,T)dλ is the power per unit area that is emitted in the wavelength interval from λ to λ+dλ.

The intensity distribution among wavelengths of radiation emitted by cavities was studied experimentally at the end of the nineteenth century. Generally, radiation emitted by materials only approximately follows the blackbody radiation curve. However, spectra of common stars do follow the blackbody radiation curve very closely.

Experimental data about blackbody radiation was obtained for various objects. Following results obtained,

• At equilibrium, the radiation emitted has a well-defined, continuous energy distribution.
• To each frequency there corresponds an energy density which depends neither on the chemical composition of the object nor on its shape, but only on the temperature of the cavity’s walls.
• The energy density shows a pronounced maximum at a given frequency, which increases with temperature; that is, the peak of the radiation spectrum occurs at a frequency that is proportional to the temperature. This is the underlying reason behind the change in colour of a heated object as its temperature increases, notably from red to yellow to white.

It turned out that the explanation of the blackbody spectrum was not so easy. The problem was that nobody was able to come up with a theoretical explanation for the spectrum of light generated by the black body. Everything classical physics could come up with went wrong.

10 Question: What is Stefan’s law ?

Solution:

The Stefan Boltzmann law describes the power radiated from a black body in terms of its temperature. Specifically, the Stefan Boltzmann law states that the total energy radiated per unit surface area of a black body across all wavelengths per unit time, is directly proportional to the fourth power of the black body's thermodynamic              temperature T
E=eσT4
where σ= 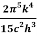=5.670373×10−8 Wm−2K−4 , Stefan Boltzmann constant.

E is the total energy radiated per unit surface area

T is the temperature of the object.

e is the emissivity (how good of a radiator/absorber the object is). The emissivity e is a correction for an approximate black body radiator, where e = 1 – R, is the fraction of the light reflected (R) by the black body. For a true black body R = 0 and e = 1 or total absorption. Which is less than or equal to 1; in the case of a blackbody e =1.

11 Question: Derive Stefan Boltzmann Law ?

Solution:

The total power radiated per unit area over all wavelengths of a black body can be obtained by integrating Plank’s radiation formula. Thus, the radiated power per unit area as a function of wavelength is:

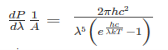……….(1)

• P is Power radiated.
• A is the surface area of a blackbody.
• λ is the wavelength of emitted radiation.
• h is Planck’s constant
• c is the velocity of light
• k is Boltzmann’s constant
• T is temperature.

On simplifying Stefan Boltzmann equation, we get:

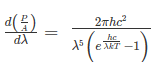
On integrating both the sides with respect to λ and applying the limits we get

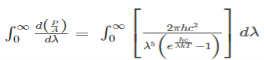
The integrated power after separating the constants is:

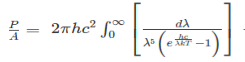……….(2)

This can be solves analytically by substituting:

x = 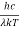……….(3)

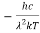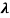
Therefore, dx= d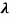

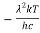d = d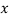……….(4)

Moreover h and c can also be written in terms of x as

h = 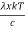……….(5)

c = 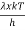……….(6)

Substituting the above equation (3),(4),(5) and (6) in equation (2)

= 2π (()2

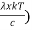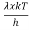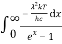
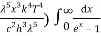
= 2π (

= 2π (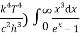……….(7)

The above equation can be comparable to the standard form of integral:

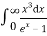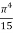= ……….(8)

So from equation (8) we can rewrite equation (7) as

= 2π (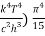

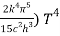=  (……….(9)

On further simplifying we get,

 = σ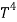……….(10)

Thus, we arrive at a mathematical form of Stephen Boltzmann law:

⇒ E = σ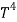……….(11)

Where,

E =

Where σ= 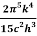=5.670373×10−8 Wm−2K−4 , Stefan Boltzmann constant.

So this is the mathematical derivation of Stefan’s Law.

12 Question: Derive expression for energy distribution of black body?

Solution:

In his 1900 attempt, Rayleigh focused on understanding the nature of the electromagnetic radiation inside the cavity. He considered the radiation to consist of standing waves having a temperature T with nodes at the metallic surfaces. These standing waves, he argued, are equivalent to harmonic oscillators, for they result from the harmonic oscillations of a large number of electrical charges, electrons that are present in the walls of the cavity. When the cavity is in thermal equilibrium, the electromagnetic energy density inside the cavity is equal to the energy density of the charged particles in the walls of the cavity; the average total energy of the radiation leaving the cavity can be obtained by multiplying the average energy of the oscillators by the number of modes (standing waves) of the radiation in the frequency interval ν to ν +d ν.

The Rayleigh-Jeans Radiation Law was a useful, but this law is not completely successful attempt at establishing the functional form of the spectra of thermal radiation.

The energy density uν per unit frequency interval at a frequency ν is, according to the The Rayleigh-Jeans Radiation,

uν =8πν2kTc2…………….(1)

Where k is Boltzmann's constant, T is the absolute temperature of the radiating body and c is the speed of light in a vacuum.

This formula fits the empirical measurements for low frequencies, but fails increasingly for higher frequencies. The failure of the formula to match the new data was called the ultraviolet catastrophe.

Derivation

Consider a cube of edge length L in which radiation is being reflected and re-reflected off its walls. Standing waves occur for radiation of a wavelength λ only if an integral number of half-wave cycles fit into an interval in the cube. For radiation parallel to an edge of the cube this requires

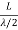=m……….(1)

Where m is an integer

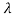
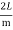=      ……….(2)

Between two end points there can be two standing waves, one for each polarization. In the following the matter of polarization will be ignored until the end of the analysis and there the number of waves will be doubled to take into account the matter of polarization.

Since the frequency ν is equal to c/λ, where c is the speed of light

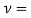
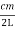……….(3)

It is convenient to work with the quantity q, known as the wavenumber, which is defined as

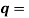
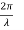……….(4)

And hence

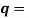
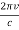  ……….(5)

In terms of the relationship for the cube,

q =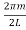 = π ( 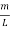)……….(6)

And hence

q2 = π2  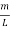( )2 ……….(7)

Another convenient term is the radian frequency ω=2πν. From this it follows that q=ω/c.

If mX, mY, mZ denote the integers for the three different directions in the cube then the condition for a standing wave in the cube is that

q2 = π2 [(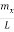)2 + (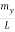)2 + ()2]……….(8)

This reduces to

m2x + m2y + m2z = 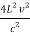……….(9)

Now the problem is to find the number of non-negative combinations of (mX, mY, mZ) that fit between a sphere of radius R and and one of radius R+dR. First the number of combinations ignoring the non-negativity requirement can be determined.

The volume of a spherical shell of inner radius R and outer radius R+dR is given by

DV=4πR2dR……….(10)

If

R = 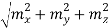……….(11)

Then

R = 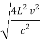= 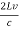……….(12)

And hence

DR = 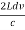……….(13)

This means that

DV = 4π(2Lν/c)2(2L/c) dν = 32π(L3v2/c3)dν……….(14)

Now the non-negativity require for the combinations (mX, mY, mZ) must be taken into account.

We know that the nonnegative combinations are in one quadrant of circle for the two dimensional case. The approximation arises from the matter of the combinations on the boundaries of the nonnegative quadrant. For the three dimensional case the nonnegative combinations constitute approximately one octant of the total. Thus the number dN for the nonnegative combinations of (mX, mY, mZ) in this volume is equal to (1/8)dV and hence

DN = 4πv2dν……….(15)

The average kinetic energy per degree of freedom is ½kT, where k is Boltzmann's constant. For harmonic oscillators there is an equality between kinetic and potential energy so the average energy per degree of freedom is kT. This means that the average radiation energy E per unit frequency is given by

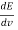= kT (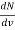) = 4πkT( 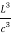)v2……….(16)

And the average energy density, uν, is given by

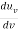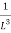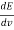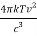=  () () =  ……….(17)

The previous only considered one direction of polarization for the radiation. If the two directions of polarization are taken into account a factor of 2 must be included in the above formula; i.e.,

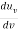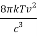= ……….(18)

This is the Raleigh-Jeans Law of Radiation and holds empirically as the frequency goes to zero.

The Rayleigh-Jeans Law was an important step in our understanding of the equilibrium radiation from a hot object, even though it turned out not to be an accurate description of nature. The careful work in developing the Rayleigh-Jeans law laid the foundation for the quantum understanding expressed in the Planck radiation formula. By Rayleigh-Jeans Law the energy density of radiation diverges at high frequencies.

This is the famous result known as the ultraviolet catastrophe– the total energy in black-body radiation diverges. This expression for the spectral energy distribution of radiation is known as the Rayleigh-Jeans Law and, although it diverges at high frequencies, it is in excellent agreement with the measured spectrum at low frequencies and high temperatures.

13 Question: What is Planck’s law ?  Derive the final result of Planck’s law?

Solution:

While Wien’s formula and the Rayleigh-Jeans Law could not explain the spectrum of a black body, Max Planck’s equation solved the problem by assuming that light was discrete.

The photoelectric effect demonstrates that light waves have particle properties and that the light quanta or photons of a particular frequency v each have energy hv. We need to reconcile this picture with the classical picture of electromagnetic waves in a box. In the classical picture, the energy associated with the waves is stored in the oscillating electric and magnetic fields.

We found it necessary to impose the constraint that only certain modes are permitted by the boundary conditions; the waves are constrained to fit into the box with whole numbers of half wavelengths in the x, y, z directions.

Now we have a further constraint. The quantisation of electromagnetic radiation means that the energy of a particular mode of frequency v  cannot have any arbitrary value but only those energies which are multiples of hν, in other words the energy of the mode is E(ν) =nhv, where we associate n photons with this mode.

We now consider all the modes (and photons) to be in thermal equilibrium at temperature T. In order to establish equilibrium, there must be ways of exchanging energy between the modes (and photons) and this can occur through interactions with any particles or oscillators within the volume or with the walls of the enclosure. We now use the Boltzmann distribution to deter-mine the expected occupancy of the modes in thermal equilibrium. The probability that a single mode has energy En=nhv is given by the usual Boltzmann factor

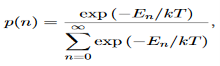   ……….(19)

Where the denominator ensures that the total probability is unity, the usual normalisation procedure. In the language of photons, this is the probability that the state contains n photons of frequency ν. The mean energy of the mode of frequency ν is therefore

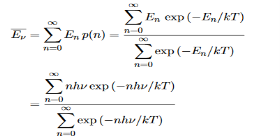
……….(20)

To simplify the calculation, let us substitute x=exp(−hν/kT). Then (20) becomes

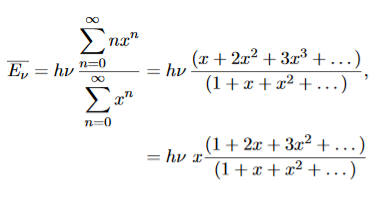……….(21)

Now, we remember the following series expansions:

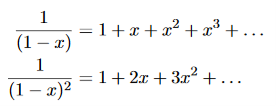………….(22)

Hence, the mean energy of the mode is

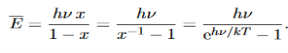………….(23)

This is the result we have been seeking. To find the classical limit, we allow the energy quanta hν to tend to zero.

Expanding ehν/kT−1 for small values of hν/kT,

ehν/kT−1 = 1 +hν/kT+!(hν/kT)2+···−1 ………….(24)

Thus, for small values of hν/kT, ehν/kT−1 =hν/kT.

And also

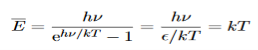…………….(25)

Thus, if we take the classical limit, we recover exactly the expression for the average energy of a harmonic oscillator in thermal equilibrium, 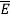=kT. We can now complete the determination of Planck’s radiation formula.

We have already shown that the number of modes in the frequency interval ν to ν+dν is (8πν2/c3) dν per unit volume. The Planck distribution in terms of the energy density of radiation per unit frequency interval

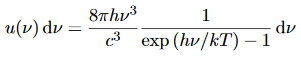
The energy density of radiation in this frequency range is

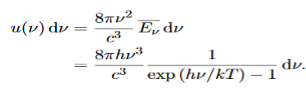………….(26)

This is the Planck distribution function.

14 Question:  Differentiate between spontaneous and stimulated emissions.

Solution:

15 Question:  Discuss Einstein’s theory of interaction of electromagnetic radiation with matter?

Solution:

Let us discuss Einstein’s theory of interaction of electromagnetic radiation with matter. He proposed that electromagnetic radiation interacts with matter in following three steps.

• Stimulated  Absorption
• Spontaneous Emission
• Stimulated Emission

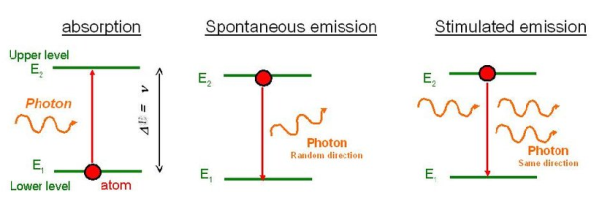
Stimulated  Absorption:

Let E1 and E2 be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground state E1 to excited state E2. This process is called stimulated absorption. Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.

Stimulated absorption rate ∝ Number of atoms in the ground state

∝   Density of photons Spontaneous emission

Spontaneous Emission:

Let E1 and E2   be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground stateE1 to excited state E2. The excited atom does not stay in a long time in the excited state. The excited atom gets de-excitation after its life time by emitting a photon of energy hν= E1− E2. This process is called spontaneous emission. Also Spontaneous means by its own. Here excited atom comes to ground state by its own so it is named as spontaneous emission.

The spontaneous emission rate depends up on the number of atoms present in the excited state.

Spontaneous emission ∝   rate number of atoms in the excited state

Stimulated Emission:

This phenomena is responsible for producing laser light. Let E1and E2 be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground stateE1 to excited state E2. Let, a photon of energy hν= E1− E2 interacts with the excited atom with in their life time; the atom gets de-excitation to ground state by emitting of another photon. These photons have same phase and it follows coherence. This phenomenon is called stimulated emission.

Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.

Stimulated emission rate ∝ number of atoms in the excited state

∝ Density of photons

16 Question:  Calculate the wavelength of radiation emitted by an LED made up of a semiconducting material with band gap energy 2.8eV.

Solution:

E = hc/ʎ
Therefore, ʎ = hc/E
ʎ = 4430.8 Å.

17 Question: Calculate the number of photons, from green light of mercury (ʎ = 4961 Å), required to do one joule of work.

Solution:

E = hc/ʎ
E = 4.006×10-19 Joules
Number of photons required = (1 Joule)/(4.006×10-19)
N = 2.4961×1018/m3.

18 Question:  Derive Einstein’s coefficient A and B ?

Solution:

The distribution of atoms in the two energy levels will change by absorption or emission of radiation. Einstein introduced three empirical coefficients to quantify the change of population of the two levels. Let N1 be the number of atoms per unit volume with energy E1 and N2 be the number of atoms per unit volume with energy E2. Let ‘n’ be the number of photons per unit volume at frequency ‘υ’ such that hυ= E1− E2.

Then, the energy density of photons ρ(υ) = nhυ

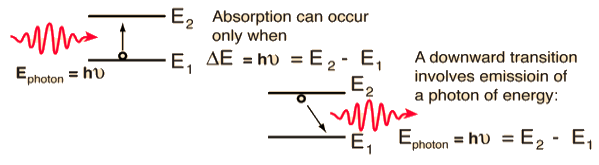
When these photons interact with atoms, both upward (absorption) and downward (emission) transition occurs.

At the equilibrium the upward transitions must be equal downward transitions.

Upward Transition

Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.

We have seen above that

Stimulated absorption rate ∝  N1 i.e. Number of atoms in the ground state

∝ ρ(υ) i.e. Density of photons spontaneous emission

Stimulated absorption rate = B12N1ρ(υ)………(1)

Where B12 is the Einstein coefficient of stimulated absorption.

Downward transition

The spontaneous emission rate depends up on the number of atoms present in the excited state.

Spontaneous emission rate ∝   N2 i.e. number of atoms in the excited state

Spontaneous emission rate = A21N2 ………(2)

Where A21 is the Einstein coefficient of spontaneous emission.

Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.

Stimulated emission rate ∝ N2 i.e. number of atoms in the excited state

∝ ρ(υ) i.e. Density of photons

Stimulated emission rate = B21N2ρ(υ)………(3)

If the system is in equilibrium the upward transitions must be equal downward transitions.

Upward transitions = downward transitions

B12N1ρ(υ) = A21N2 + B21N2ρ(υ)………(4)

B12N1ρ(υ) - B21N2ρ(υ) = A21N2

(B12N1- B21N2) ρ(υ) = A21N2

ρ(υ) =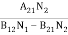………(5)

Divide with B21N2 in numerator and denominator in right side of the above equation,

ρ(υ) = 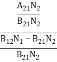 =  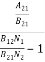………(6)

ρ(υ) = 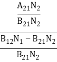 = =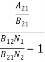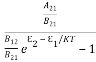………(7)

We know from Maxwell Boltzmann distribution law

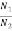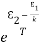= ………(8)

And also from Planck’s law, the radiation density

ρ(υ)  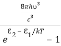= ………(9)

Comparing the two equations (7) and (9)

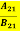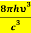=    and =1………(10)

The above relations referred to as Einstein relations.

From the above equation for non degenerate energy levels the stimulated emission rate is equal to the stimulated absorption rate at the equilibrium condition.

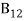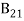= ………(11)

19 Question:  What is the relationship between B21 and B12?
a) B12 > B21
b) B12 < B21
c) B12 = B21
d) No specific relation
 

Solution:

C is the correct answer.
B21 is the coefficient for the stimulated emission while B12 is the coefficient for stimulated absorption. Both the processes are mutually reverse processes and their probabilities are equal. Therefore, B12 = B21.

20 Question:  Discuss construction, working and application of gas Laser?

Or

Discuss construction, working and application of He-Ne Laser?

Or

Discuss four level laser ?

Solution:

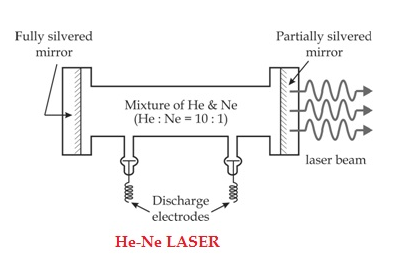
He-Ne Laser

The first He-Ne gas laser was fabricated in 1961 by Ali Javan, Bennett and Herriott at Bell Telephone Laboratories. others. Helium-Neon laser is a type of gas laser in which a mixture of helium and neon gas is used as a gain medium. Helium-Neon laser is also known as He-Ne laser. The helium-neon laser was the first continuous wave laser ever constructed. The helium-neon laser operates at a wavelength of 632.8 nanometres (nm), in the red portion of the visible spectrum.

Ruby laser is a pulse laser, even it have high intense output. For continuous laser beam gas lasers are used. Using gas lasers, we can achieve highly coherence, high directionality and high monochromacity beam. The output power of the gas laser is generally in few milliwatts.

Construction

The helium-neon laser consists of three essential components:

• Pump source (high voltage power supply)
• Gain medium (laser glass tube or discharge glass tube)
• Resonating cavity

Pump source

The gain medium of a helium-neon laser is made up of the mixture of helium and neon gas contained in a glass tube at low pressure. In He-Ne gas laser, the He and Ne gases are taken in the ratio 10:1 in the discharge tube.

Gain medium

In He-Ne laser 80cm length and 1cm diameter discharge is generally used. The out power of these lasers depends on the length of the discharge tube and pressure of the gas mixture. Therefore, in order to achieve population inversion, we need to pump electrons from lower energy state of the helium. In He-Ne laser, neon atoms are the active centres and have energy levels suitable for laser transitions while helium atoms help in exciting neon atoms.

Resonating cavity

Two reflecting mirrors are fixed on either ends of the discharge tube, in that, one is partially reflecting and the other is fully reflecting. The fully silvered mirror will completely reflect the light whereas the partially silvered mirror will reflect most part of the light but allows some part of the light to produce the laser beam.

Working

When the electric discharge is passing through the gas mixture, the electrons accelerated towards the positive electrode. During their passage, they collide with He atoms and excite them into higher levels. 23s1 and 21s0 form ground state of He atom. In higher levels 23s1 and 21s0, the life time of He atoms is more. So there is a maximum possibility of energy transfer between He and Ne atoms through atomic collisions. When He atoms present in the levels 23s1 and 21s0  collide with Ne atoms present ground state, the Ne atoms gets excitation into higher levels 4s and 5s.

Due to the continuous excitation of Ne atoms, we can achieve the population inversion between the higher levels 4s and 5s  and lower levels 3p and 4p. The various transitions 5s to 4p, 4s to 3p and 5s to 3p leads to the emission of wavelengths  3.93μm, 1.51μm and 6328 Å or 632.8μm.

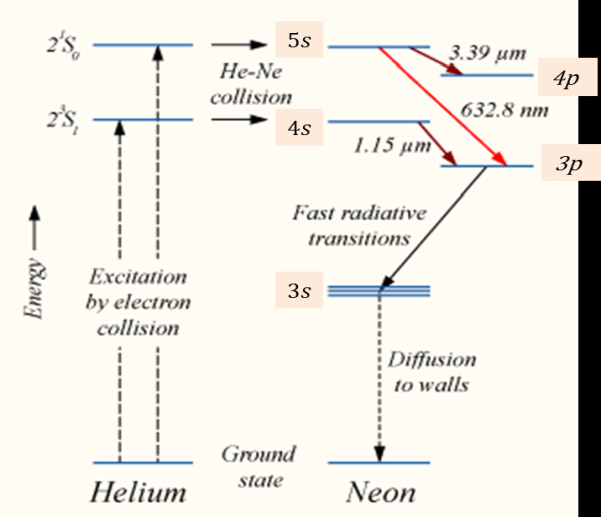
The first two corresponding to the infrared region while the last wavelength is corresponding to the visible region. The Ne atoms present in the 4s level are de-excited into 3s level, by spontaneously emitting a photon of around wavelength 6000 Å. When a narrow discharge tube is used, the Ne atoms present in the level 3s collide with the walls of the tube and get de-excited to ground state energy level.

Advantages of helium-neon laser

• Helium-neon laser emits laser light in the visible portion of the spectrum.
• High stability
• Low cost
• Operates without damage at higher temperatures

Disadvantages of helium-neon laser

• Low efficiency
• Low gain
• Helium-neon lasers are limited to low power tasks

Applications of helium-neon lasers

• Helium-neon lasers are used in industries.
• Helium-neon lasers are used in scientific instruments.
• Helium-neon lasers are used  in the college laboratories

21 Question:  Discuss Properties Of Laser Beams?

Solution:

The laser light exhibits some peculiar properties than compare with the convectional light. Those are

1. Highly monochromatic

2. Highly coherence

3. Highly directionality

4. Highly intense

1. Highly monochromatic

Monochromatic light means a light containing a single colour or wavelength. The photons emitted from ordinary light sources have different energies, frequencies, wavelengths, or colours. Ordinary light is a mixture of waves having different frequencies or wavelengths. The light waves of laser have single wavelength or colour.

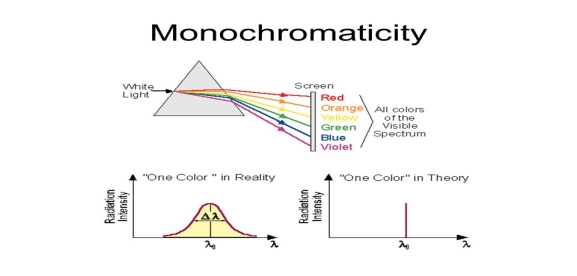
Therefore, laser light covers a very narrow range of frequencies or wavelengths.

Hence The laser light is more monochromatic than that of a convectional light source. This may be due to the stimulated characteristic of laser light. The band width of convectional monochromatic light source is 1000 Å. But the band width of ordinary light source is 10 Å. For high sensitive laser source is 10-8 Å.

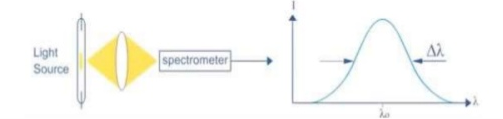
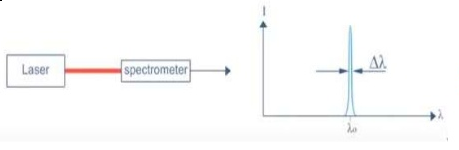
2. Highly coherence

Definition:- A predictable correlation of the amplitude and phase at any one point with other point is called coherence.

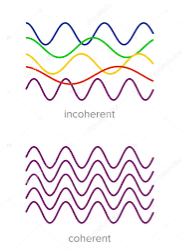
Two waves are said to be coherent, the waves must have

In case of convectional light, the property of coherence exhibits between a source and its virtual source where as in case of laser the property coherence exists between any two of more light waves.

There are two types of coherence

i)                   Temporal coherence

Ii)                Spatial coherence

Temporal coherence (or longitudinal coherence):-

The predictable correlation of amplitude and phase at one point on the wave train w .r. t another point on the same wave train, then the wave is said to be temporal coherence

To understand this, let us consider two points P1 and P2 on the same wave train, which is continuous as in shown in figure.

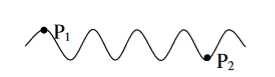
Suppose the phase and amplitude at any one point is known, then we can easily calculate the amplitude and phase for any other point on the same wave train by using the wave equation

y= a sin (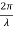 (ct-x))

Where ‘a’ is the amplitude of the wave and ‘x’ is the displacement of the wave at any instant of time‘t’.

Spatial coherence (or transverse coherence) The predictable correlation of amplitude and phase at one point on the wave train w. r .t another point on a second wave, then the waves are said to be spatial coherence (or transverse coherence)

3. Highly directionality

The light ray coming ordinary light source travels in all directions, but laser light travels in single direction. For example the light emitted from torch light spreads 1km distance it spreads 1 km distance. But the laser light spreads a few centimetres distance even it travels lacks of kilometre distance.

The directionality of laser beam is expressed in terms of divergence

∆θ =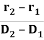

Where r1 and r2  are the radii of laser bam spots at distances of D1  and D2  respectively from laser source.

4. Highly Intense or Brightness

We know that the intensity of a wave is the energy per unit time flowing through a unit normal area. Laser light is highly intense than the convectional light. An one mill watt He-Ne laser is highly intense than the sun intensity. This is because of coherence and directionality of laser. Suppose when two photons each of amplitude a are in phase with other, then young’s principle of superposition, the resultant amplitude of two photons is 2a and the intensity is 4a2.  Since in laser many number of photons are in phase with each other, the amplitude of the resulting wave becomes na and hence the intensity of laser is proportional to n2a2.  So 1mW He-Ne laser is highly intense than the sun.

In an ordinary light source, the light spreads out uniformly in all directions. If you look at a 100 Watt lamp filament from a distance of 30 cm, the power entering your eye is less than 1/1000 of a watt. If you look laser beam  X(caution: don’t do it at home, direct laser light can damage your eyes)X, then all the power in the laser would enter your eye.  Thus, even a 1 Watt laser would appear many thousand times more intense than 100 Watt ordinary lamp.

22 Question:  What is coherence? 

Solution:

Definition:- A predictable correlation of the amplitude and phase at any one point with other point is called coherence.

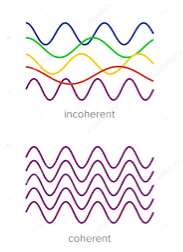
Two waves are said to be coherent, the waves must have

In case of convectional light, the property of coherence exhibits between a source and its virtual source where as in case of laser the property coherence exists between any two of more light waves.

There are two types of coherence

i)                   Temporal coherence

Ii)                Spatial coherence

Temporal coherence (or longitudinal coherence):-

The predictable correlation of amplitude and phase at one point on the wave train w .r. t another point on the same wave train, then the wave is said to be temporal coherence

To understand this, let us consider two points P1 and P2 on the same wave train, which is continuous as in shown in figure.

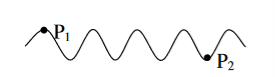
Suppose the phase and amplitude at any one point is known, then we can easily calculate the amplitude and phase for any other point on the same wave train by using the wave equation

y= a sin (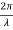 (ct-x))

Where ‘a’ is the amplitude of the wave and ‘x’ is the displacement of the wave at any instant of time‘t’.

Spatial coherence (or transverse coherence) The predictable correlation of amplitude and phase at one point on the wave train w. r .t another point on a second wave, then the waves are said to be spatial coherence (or transverse coherence)

23 Question:  Discuss Applications Of Lasers In various fields?

Solution:

Applications of lasers because of unique property of laser beam such as coherence, monochromacity, directionality, and high intensity, they are widely used in various fields like

1. Communication

2. Computers

3. Chemistry

4. Photography

5. Industry

6. Medicine

7. Military

8. Scientific Research

1. Communication

In case of optical communication semiconductors laser diodes are used as optical sources and its band width is (1014Hz) is very high compared to the radio and microwave communications.  More channels can be sent simultaneously Signal cannot be tapped as the band width is large, more data can be sent. A laser is highly directional and less divergence, hence it has greater potential use in space crafts and submarine. It is used in optical fiber communications to send information over large distances with low loss. Laser light is used in underwater communication networks. Lasers are used in space communication, radars and satellites.

2. Computers 

In LAN (local area network), data can be transferred from memory storage of one computer to other computer using laser for short time.  Lasers are used in CD-ROMS during recording and reading the data. Lasers are used in computer printers.

3. Chemistry

Lasers are used in molecular structure identification Lasers are also used to accelerate some chemical reactions.  Using lasers, new chemical compounds can be created by breaking bonds between atoms are molecules.

4. Photography

Lasers can be used to get 3-D lens less photography.  Lasers are also used in the construction of holograms.

5. Industry 

Lasers can be used to blast holes in diamonds and hard steel. Lasers are also used as a source of intense heat Carbon dioxide laser is used for cutting drilling of metals and non-metals, such as ceramics plastics glass etc.  High power lasers are used to weld or melt any material.  Lasers are also used to cut teeth in saws and test the quality of fabric. It is used to cut glass and quartz, used in electronic industries for trimming the components of Integrated Circuits (ICs).Lasers are used for heat treatment in the automotive industry. Laser light is used to collect the information about the prefixed prices of various products in shops and business establishments from the bar code printed on the product. Ultraviolet lasers are used in the semiconductor industries for photolithography. Photolithography is the method used for manufacturing printed circuit board (PCB) and microprocessor by using ultraviolet light. It is also  used to drill aerosol nozzles and control orifices within the required precision.

6. Medicine

Pulsed neodymium laser is employed in the treatment of liver cancer.  Argon and carbon dioxide lasers are used in the treat men of liver and lungs.  Lasers used in the treatment of Glaucoma.

Lasers used in endoscopy to scan the inner parts of the stomach.  Lasers used in the elimination of moles and tumors which are developing in the skin tissue and hair removal. It is also used for bloodless surgery.

Lasers are used to destroy kidney stones, in cancer diagnosis and therapy also used for eye lens curvature corrections. Lasers are used to study the internal structure of microorganisms and cells. It is used to create plasma. Lasers are used to remove the caries or decayed portion of the teeth.

7. Military

Lasers can be used as a war weapon. High energy lasers are used to destroy the enemy air-crofts and missiles. Lasers can be used in the detection and ranging likes RADAR. Laser range finders are used to determine the distance to an object. The ring laser gyroscope is used for sensing and measuring very small angle of rotation of the moving objects.

Lasers can be used as a secretive illuminators for reconnaissance during night with high precision.

8. Scientific research

Lasers are used in the field of 3D-photography Lasers used in Recording and reconstruction of hologram. Lasers are employed to create plasma. Lasers are used in Raman spectroscopy to identify the structure of the molecule and to count the number of atoms in a substance. Lasers are used in the Michelson- Morley experiment. A laser beam is used to confirm Doppler shifts in frequency for moving objects. A laser helps in studying the Brownian motion of particles. With the help of a helium-neon laser, it was proved that the velocity of light is same in all directions. Lasers are used to measure the pollutant gases and other contaminants of the atmosphere. Lasers help in determining the rate of rotation of the earth accurately. Lasers are used for detecting earthquakes and underwater nuclear blasts. A gallium arsenide diode laser can be used to setup an invisible fence to protect an area.

24 Question:  Discuss construction, working and application of Solid-State Laser?

Or

Discuss construction, working and application of Ruby Laser?

Or

Discuss three level laser ?

Solution:

Ruby laser

Ruby laser is a three level solid state laser and was constructed by Maiman in 1960. Ruby laser is one of the few solid-state lasers that produce visible light. It emits deep red light of wavelength 694.3 nm.

Construction

A ruby laser consists of three important elements: laser medium, the pump source and the optical resonator.

Laser Medium

Ruby (Al2O3+Cr2O3) is a crystal of Aluminium oxide, in which 0.05% of Al+3 ions are replaced by the Cr+3 ions. The colour of the rod is pink. The active medium or laser medium in the ruby rod is Cr+3 ions. In ruby laser 4cm length and 5mm diameter rod is generally used. The ruby has good thermal properties.

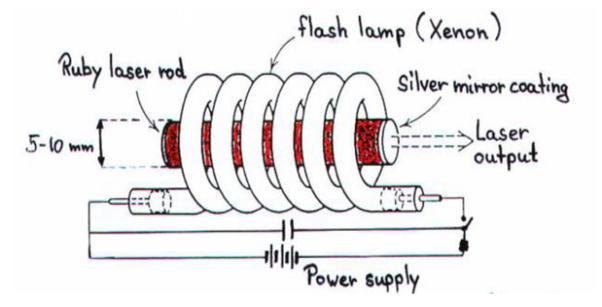
The pump source

The ruby rod is surrounded by xenon flash tube, which provides the pumping light to excite the chromium ions in to upper energy levels. The ruby rod was surrounded by a helical xenon flash lamp.

We know that population inversion is required to achieve laser emission. Population inversion is the process of achieving the greater population of higher energy state than the lower energy state. In order to achieve population inversion, we need to supply energy to the laser medium i.e. to ruby crystal.

Xenon flash tube emits thousands joules of energy in few milliseconds, but only a        part of that energy is utilized by the chromium ions while the rest energy heats up the apparatus. A cooling arrangement is provided to keep the experimental set up at normal temperatures.

Optical resonator

Both the ends of the rods are highly polished and made strictly parallel. The ends are silvered in such a way, one becomes partially reflected the laser beam was emitted through that end and the other end fully reflected to reflect all the rays of light striking it.

Working of ruby laser:

Consider a ruby laser medium consisting of three energy levels E1, E2, E3 with N number of electrons.

We assume that the energy levels will be E1 < E2 < E3. The energy level E1 is known as ground state or lower energy state, the energy level E2 is known as metastable state, and the energy level E3 is known as pump state.

Let us assume that initially most of the electrons are in the lower energy state (E1) and only a tiny number of electrons are in the excited states (E2 and E3).

The energy level diagram of chromium ions is shown in figure. The chromium ions get excitation into higher energy levels by absorbing of 5500Å of wavelength radiation. The excited chromium ions stay in the level E3 for short interval of time (10-8 to 10-9 Sec). After their life time most of the chromium ions are de-excited from E3 to E1 and a few chromium ions are de-excited from E3 to E2.

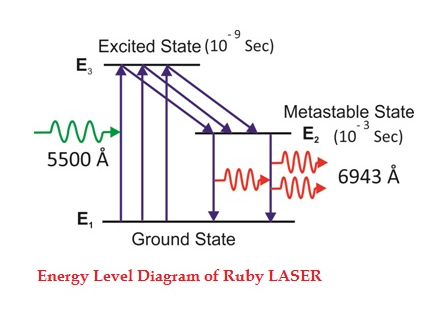
The transition between E3 and E2 is non-radioactive transition i.e. the chromium ions gives their energy to the lattice in the form of heat. In the Meta stable state the life time of chromium ions is 10-3 sec. The life time of chromium ions in the Meta stable state is 105 times greater than the life time of chromium ions in higher state.

Due to the continuous working of flash lamp, the chromium ions are excited to higher state E3 and returned to E2 level. After few milliseconds the level E2 is more populated than the level E1 and hence the desired population inversion is achieved. The state of population inversion is not a stable one. The process of spontaneous transition is very high. When the excited chromium ion passes spontaneously from E3 to E2it emits one photon of wave length 6943 Å. The photon reflects back and forth by the silver ends and until it stimulates an excited chromium ion in E2 state and it to emit fresh photon in phase with the earlier photon. The process is repeated again and again until the laser beam intensity is reached to a sufficient value. When the photon beam becomes sufficient intense, it emerges through the partially silvered end of the rod. The wave length 6943 Å is in the red region of the visible spectrum.

Draw backs of ruby laser

• The laser requires high pumping power 
• The efficiency of ruby laser is very small
• It is a pulse laser

 Application of ruby laser

• Ruby lasers are in optical photography
• Ruby lasers can be used for measurement of plasma properties such as electron density and temperature.
• Ruby lasers are used to remove the melanin of the skin.
• Ruby laser can be used for recording of holograms.

25 Question: How laser light get amplify by population inversion ?

Solution:

Population inversion

Definition

The number of atoms present in the excited state or higher energy state is greater than the number of atoms present in the ground state or lower energy state is called population inversion.

Population inversion as name suggests that this is inverted phenomena. In general lower energy level is more populated that means it have more number of atoms in lower energy level as compared to higher energy level. But by pumping we will obtain a state when the number of atoms present in the higher energy state is greater than the number of atoms present in lower energy state.

Let us consider two level energy system of energies E1 and E2 as shown in figure.

Let N1 and N2 be the populations that means number of atoms per unit volume of energy levels E1 and E2 respectively.

According to Boltzmann’s distribution the population of an energy level E, at temperature T is given by

Ni=N0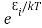

Where N0 is the population of the lower level or ground state and k is the Boltzmann’s constant.

From the above relation, the population of energy levels E1 and E2  are

N1=N0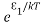

N2=N0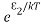

At ordinary conditions N1 >N2 i.e., the population in the ground or lower state is always greater than the population in the excited or higher states. The stage of making, population of higher energy level is greater than the population of lower energy level is called population inversion i.e. N1 < N2

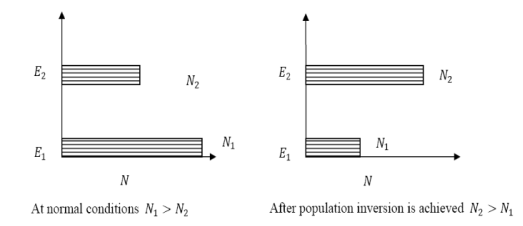
When population inversion method is used to enforce more and more atoms to give up photons. This initiates a chain reaction and releasing massive amount of energy.

This results in rapid build-up of energy of emitting one particular wavelength traveling coherently in fixed direction. This process is called amplification by stimulated emission using population inversion.

This population inversion situation is essential for a laser action. For any stimulated emission, It is necessary that the upper energy level or meta stable state should have a long life time, i.e., the atoms should pause at the meta stable state for more time than at the lower level.

26 Question:  What is Pumping?  Discuss various type of pumping mechanisms?

Solution:

For laser action, pumping mechanism (exciting with external source) maintain a higher population of atoms in the upper energy level relative to that in the lower level.

A system in which population inversion is achieved is called as an active system. The method of raising the particles from lower energy state to higher energy state is called pumping.

The process of achieving of population inversion is called pumping.

This can be done by number of ways.

The most commonly used pumping methods are

1. Optical pumping
2. Electrical discharge pumping
3. Chemical pumping
4. Thermal Pumping
5. Injection current pumping
6. Inelastic Atom-Atom Collisions

Optical pumping As the name suggests, in this method, light is used to supply energy to the laser medium. Optical pumping is used in solid laser. Xenon flash tubes are used for optical pumping. Since these materials have very broad band absorption, sufficient amount of energy is absorbed from the emission band of flash lamp and population inversion is created. So xenon flash lamp is used to produce more electrons in the higher energy level of the laser medium.

Examples of optically pumped lasers are ruby, Nd: YAG Laser(Neodymium: Yttrium Aluminum Garnet).

Electrical discharge pumping Electrical discharge pumping is used in gas lasers. Since gas lasers have very narrow absorption band pumping then any flash lamp is not possible. Electric discharge refers to flow of electrons or electric current through a gas, liquid or solid.

In this method of pumping, electric discharge acts as the pump source or energy source. A high voltage electric discharge (flow of electrons, electric charge, or electric current) is passed through the laser medium or gas. The intense electric field accelerates the electrons to high speeds and they collide with neutral atoms in the gas. As a result, the electrons in the lower energy state gains sufficient energy from external electrons and jumps into the higher energy state

 Examples of Electrical discharge pumped lasers are He-Ne laser, CO2 laser, argon-ion laser etc.

Chemical pumping Chemical reaction may also result in excitation and hence creation of population inversion in few systems.

 If an atom or a molecule is produced through some chemical reaction and remains in an excited state at the time of production, then it can be used for pumping. The hydrogen fluoride molecule is produced in an excited state when hydrogen and fluorine gas chemically combine. The number of produced excited atoms or molecules is greater than the number of normal state atoms or molecules. Thus, population inversion is achieved.

Examples H2 + F2 → 2HF, in this chemical reaction, hydrogen (H2) and fluorine (F2) molecules are chemically combined to produce hydrogen fluoride molecule (2HF) in an excited state.

Thermal Pumping: Sometimes we can achieve population inversion by heating the laser medium. In thermal pumping, heat acts as the pump source or energy source. In this method, population inversion is achieved by supplying heat into the laser medium.

When heat energy is supplied to the laser medium, the lower energy state electrons gains sufficient energy and jumps into the higher energy level.

The process of achieving population inversion in thermal pumping is almost similar to the optical pumping or electric discharge method, except that in this method heat is used as pump source instead of light or electric discharge.

Injection current pumping In semiconductors, injection of current through the junction results in creates of population inversion among the minority charge carriers.

Examples of such systems are InP and GaAs.

Inelastic Atom-Atom Collisions: Like the electric discharge method, here also a high voltage electric discharge acts as a pump source. However, in this method, a combination of two types of gases, say X and Y are used. The excited state of gas X is represented as X+ whereas gas Y is represented as Y+. Both X and Y gases have the same excited states (X+ and Y+).

When high voltage electric discharge passes through a laser medium having two types of gases X and Y, the lower energy state electrons in gas X will move to the excited state X+ similarly the lower energy state electrons in gas Y moves to the excited state Y+.

Initially, during electric discharge, the lower energy state electrons in gas X or atom X gets excited to X+ due to continuous collision with electrons. The excited state electrons in gas X+ now collide with the lower energy state electrons in gas Y. As a result, the lower energy state electrons in gas Y gains sufficient energy and jump into the excited state Y+. This method is used in the Helium–Neon (He-Ne) laser.

27 Question:  Why Two-level laser is not possible? Give valid reason.

Solution:

Consider a group of electrons with two energy levels E1 and E2.

E1 is the lower energy state and E2 is the higher energy state.
N1 is the number of electrons in the energy state E1.
N2 is the number of electrons in the energy state E2.
 

The number of electrons per unit volume in an energy state is the population of that energy state.

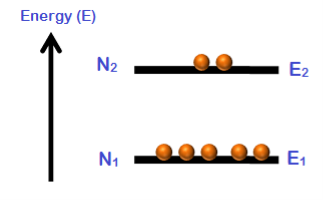
Population inversion cannot be achieved in a two energy level system. Under normal conditions, the number of electrons (N1) in the lower energy state (E1) is always greater as compared to the number of electrons (N2) in the higher energy state (E2).

N1 > N2

When temperature increases, the population of higher energy state (N2) also increases. However, the population of higher energy state (N2) will never exceeds the population of lower energy state (N1).

At best an equal population of the two states can be achieved which results in no optical gain.

N1 = N2

Two energy level lasers are not possible. We can not get population inversion in a 2 level LASER no matter how much we pump the atoms in the ground state. And since population inversion is a necessity for lasing action, we don't have two level lasers.

Therefore, we need 3 or more energy states to achieve population inversion. The greater is the number of energy states the greater is the optical gain.

There are certain substances in which the electrons once excited; they remain in the higher energy level or excited state for longer period. Such systems are called active systems or active media which are generally mixture of different elements.

When such mixtures are formed, their electronic energy levels are modified and some of them acquire special properties. Such types of materials are used to form 3-level laser or 4-level laser.