Module 1

Atomic and molecular structure

Question Bank

1. Explain the Schrodinger’s Wave Equation?

Is a very fundamental equation used in quantum physics it is also referred as just Schrodinger equation, it’s basically a differential equation used to solve problems, that are based on structure of atoms. The equation is used widely in Physics and Chemistry.

Schrodinger wave equation describes the change of a physical quantity with time or the behaviour of a particle in a field of force. Erwin Schrödinger was the one developed the equation was even awarded the Nobel Prize in 1933. Schrodinger wave equation is a mathematical expression that describes the energy and position of the electron present in space and time, taking into account the matter wave nature of the electron inside an atom

Schrodinger equation gives us a detailed account of the wave probability that hold the movement of some particles, the equation gives a detail of the form of wave functions. The equation also details, how these waves are however influenced by external factors. Moreover, the equation makes use of the energy conservation concept that offers details about the behaviour of an electron that is attached to the nucleus.

Besides, by calculating the Schrödinger equation we obtain Ψ and Ψ2 which helps us determine the quantum numbers as well as the orientations and the shape of orbitals where electrons are found in a molecule or an atom.

There are two equations which are time-dependent Schrödinger equation and a time-independent Schrödinger equation

The Time-dependent Schrödinger equation is represented as;

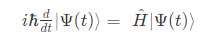
The Time-dependent Schrödinger equation in position basis is given as

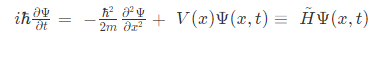
Where,

i = imaginary unit, Ψ = time-dependent wavefunction, h2 is h-bar, V(x) = potential and

H^    = Hamiltonian operator

2.     Write two properties of Molecular orbitals?

Molecular orbitals are approximate solutions to the Schrodinger’s Equation for the electrons in the electric field of the molecule's atomic nuclei. However, calculating the orbitals directly from this equation is far too intractable a problem. Instead they are obtained from the combination of atomic orbitals, which predict the location of an electron in an atom. A molecular orbital can specify the electron configuration of a molecule

Molecular orbitals are, in general, delocalized throughout the entire molecule. Moreover, if the molecule has symmetry elements, its nondegenerate molecular orbitals are either symmetric or antisymmetric with respect to any of these symmetries

Transition metals are defined as those elements that have (or readily form) partially filled d orbitals. They have large charge/radius ratio are hard and have high densities, have high melting and boiling points; form compounds which are often paramagnetic;

4.     Explain the Particle in a box concept?

In Quantum Physics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly utilized as a hypothetical example to describe the differences between quantum and classical systems. For example, in classical systems, a particle trapped inside a large box moves more freely and cannot be spotted in a single position and can move at any speed within the box. However, when the space becomes very narrow (on the scale of a few nanometres), quantum effects become very important. The particle may only occupy certain positive energy levels. Likewise, the particle can never have zero energy, meaning that the particle can never "sit still" or be stationary. Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.

The particle in a box model found in quantum mechanics is one of the very few problems which can be solved analytically, without approximations. As the particle shows its simplicity, and without the need of mathematics, the model allows insight into quantum effects without the need for complications. It serves as a simple illustration of how energy quantization’s (energy levels), which are found in more complicated quantum systems such as atoms and molecules, are present.

The Schrödinger equation differentiates particles based on their potential they lie in. For a free particle, previously discussed, we assumed the most basic potential: no potential, V(x)=0. This describes a free particle, but assumes that the particle will never experience a potential at any x-position it occupies. This is unrealistic, and hence we need to start moulding our potential to account for this experimental result. In atomic systems, there are places where an electron will NEVER be (or more accurately, it is extremely unlikely). In order to constrain the electron from ever occupying these locations we will set the potential at these locations to be infinity (the potential barrier to occupy that location cannot be overcome).

          For real applications of this type of problem, we can look at conjugated polymers (series of double bonds or aromatic groups). For these systems, electrons can move (almost) freely inside the band gap (fermi level); however, they cannot escape the molecule (it is not a conductor). The most famous example of these conjugated system (modelled almost exactly by this type of approximation) is the quantum dot: small semiconductors whose colour can be changed based on the size of the dot.

          We call this type of problem the "infinite square well" or "particle in a box" and it can be pictorially modelled as:

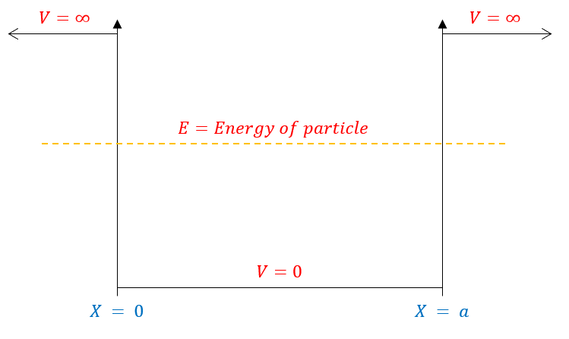
As one can visually see, the potential is now a piecewise function. We can therefore break up the Schrödinger equation into a part where the potential is infinity and a part where the potential is zero. 

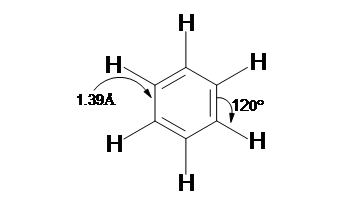
• Benzene (C6H6) structure consists of a ring of six carbon atoms each of these carbon atoms is attached with a hydrogen atom and is a planar molecule.
• A perfect regular hexagon shape is obtained with the six carbon atoms. All of the carbon-carbon bonds present in the Benzene the exact similar lengths somewhere between single and double bonds.
• The Benzene molecule is partially unstable due to the presence of delocalized electrons above and below the plane of the ring.
• Benzene is known to resist reactions that involve addition reactions as these reactions would break the delocalization and the stability is lost.

The resulting molecule of Benzene is planar in shape because of the aromaticity of benzene, the resulting molecule of benzene consists of each C-C bond being 1.39 Å in length and each bond angle being 120°. This brings us to consider how it's possible to have all of the bonds to be the same length if the ring is conjugated with both single (1.47 Å) and double (1.34 Å), a very important aspect here to be noted is that there is absence of distinct single or double bonds present within the benzene. Rather, when the ring is delocalized then the ring makes each count as one and a half bonds between the carbons this can however be proved experimentally as the actual bond length lies somewhere in between a single and double bond. Finally, there are a total of six p-orbital electrons that form stable electron clouds above and below the aromatic ring.

If the temperature is increased for a reaction or a catalyst is added to the reaction and if benzene is forced to react under these conditions, then benzene undergoes substitution reactions rather than the addition reactions that are typical seen in alkenes. These reactions prove that benzene core that has a six carbon is stable to chemical modifications.  The mutual contrast that is shown by a high degree of unsaturation (low H:C ratio) and high chemical stability for benzene and related compounds remained an unsolved mystery. Eventually, the planar ring of carbons and the regular hexagon structure was adapted, and the chemical stability and exceptional thermodynamic systems was attributed to resonance stabilization of a conjugated cyclic triene

Transition metals are defined as those elements that have (or readily form) partially filled d orbitals. They have large charge/radius ratio are hard and have high densities, have high melting and boiling points; form compounds which are often paramagnetic;

7.                 What are heteronuclearmolecules?

A heteronuclear molecule is a molecule composed of atoms of more than one chemical element. For example, a molecule of water (H 2 O) is heteronuclear because it has atoms of two different elements, hydrogen (H) and oxygen (O). Similarly, a heteronuclear ion is an ion that contains atoms of more than one chemical element.

8.                 Mention any one theory which failed to explain paramagnetic properties?

Electrons in a molecule occupy atomic orbitals rather than molecular orbitals. The atomic orbitals overlap on the bond formation and the larger the overlap the stronger the bond, Valence bond theory predicts that all electrons in diatomic oxygen are spin paired, making O2 diamagnetic.  However, diatomic oxygen is paramagnetic.  This means that electrons are not spin paired.  

9.                 Explain the crystal field theory?

The Crystal field theory (CFT) is a model for the bonding interaction between transition metals and ligands. It describes the effect of attraction between the positive charge of the metal cation and negative charge on the non-bonding electrons of a ligand. When the ligand approaches the central metal ion the dangerously of electronic orbital states, usually d or f orbitals, are broken due to the statistic electric field by a surrounding charge distribution. CFT successfully accounts for some magnetic properties, colours, hydration energies of transition metal complexes, but it does not help to describe bonding.

10.             Write briefly about Geometrics?

Different ligand structural arrangements result from coordination number. Most structures follow the pattern, central atom in the middle and the corners of that shape are the location of the ligands. These shapes are defined by orbital overlap between ligand and metal orbital and ligand-ligand repulsions, which tend to lead to certain regular geometrics. However, there are many cases that deviate from regular geometry. For example, ligands of different sizes and with different electronic effects often results in irregular bond lengths.