Question Bank
UNIT–2
Multivariable Calculus
Question-1: Test the continuity of the following function-

Sol. (1) the function is well defined at (0,0)
(2) check for the second step,
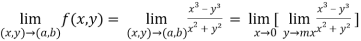

That means the limit exists at (0,0)
Now check step-3:
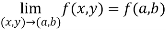

So that the function is continuous at origin.
Question-2: Evaluate 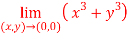
Sol . 1. 
2. 
Here f1 = f2
3. Now put y = mx, we get

Here f1 = f2 = f3
Now put y = mx²
4. 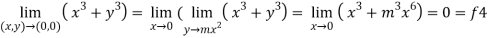
Therefore ,
F1 = f2 = f3 =f4
We can say that the limit exists with 0.
Question-3: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Sol. 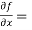 3x²y² - y⁵,
3x²y² - y⁵,  2x³y – 5xy⁴,
2x³y – 5xy⁴,
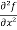 =
= 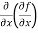 = 6xy²
= 6xy²
 =
=  2x³ - 20xy³
2x³ - 20xy³
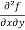 =
= 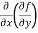 = 6x²y – 5y⁴
= 6x²y – 5y⁴
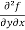 =
= 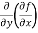 = 6x²y - 5y⁴
= 6x²y - 5y⁴
Question-4: if 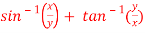 , then show that-
, then show that- 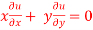
Sol. Here we have,
u = 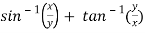 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get

= 
Or

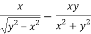 ………………..(2)
………………..(2)
And now,

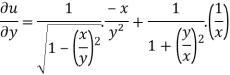
= 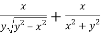
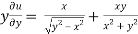 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
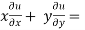
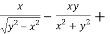
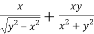 = 0
= 0
Hence proved.
Question-5: if w = x² + y – z + sint and x + y = t, find
(a) 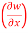 y,z
y,z
(b)  t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x² + y - z + sin (x + y).
Therefore,
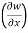 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y) (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
thus 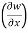 t, z = 2x - 1
t, z = 2x - 1
Question-6: If z is the function of x and y , and x =  , y =
, y =  , then prove that,
, then prove that,
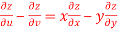
Sol. Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
 ……………….(1)
……………….(1)
And,
 ………………..(2)
………………..(2)
Also there is,
x = 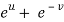 and y =
and y = 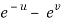 ,
,
Now,
 ,
, 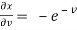 ,
, 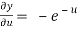 ,
, 
From equation(1) , we get
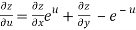 ……………….(3)
……………….(3)
And from eq. (2) , we get
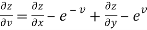 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get

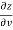 =
= 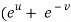 )
)  – (
– (
= x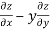
Hence proved.
Question-7: Find the equation of the tangent plane and normal line to the surface 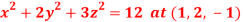
Sol.
Here,
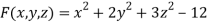
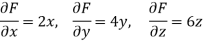
At point (1, 2, -1)-
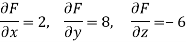
Therefore the equation of the tangent plane at (1, 2, -1) is-
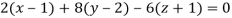


Equation of normal line is-
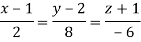
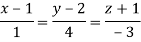
Question-8: Find the point on plane 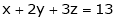 nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
Solution:
Let 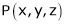 be the point on sphere
be the point on sphere 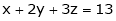 which is nearest to the point
which is nearest to the point 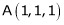 . Then shortest distance.
. Then shortest distance.
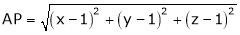
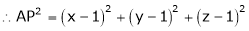
 Let
Let 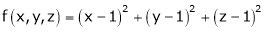
Under the condition 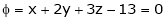 … (1)
… (1)
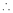 By method of Lagrange’s undetermined multipliers we have
By method of Lagrange’s undetermined multipliers we have

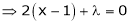 … (2)
… (2)
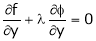
 … (3)
… (3)
i.e.  &
&
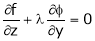
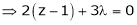 … (4)
… (4)
From (2) we get 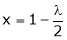
From (3) we get 
From (4) we get 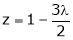
 Equation (1) becomes
Equation (1) becomes
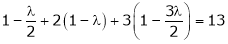
i.e. 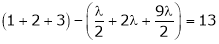

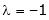

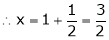
y = 2
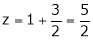
Question-9: Evaluate 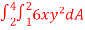 , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
Sol. Let , I = 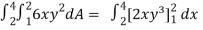
= 
= 
= 
= 84 sq. Unit.
Which is the required area.
Question-10: Evaluate 
Sol. Let us suppose the integral is I,
I = 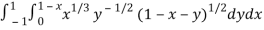
Put c = 1 – x in I, we get
I = 
Suppose , y = ct
then dy = c
Now we get,
I = 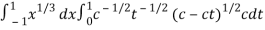
I = 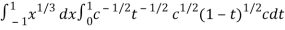
I = 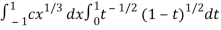
I = 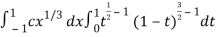
I = 
As we know that by beta function,
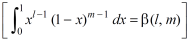
Which gives,
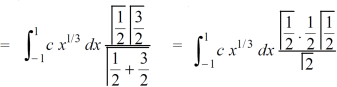
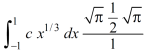
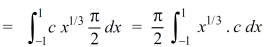
Now put the value of c, we get
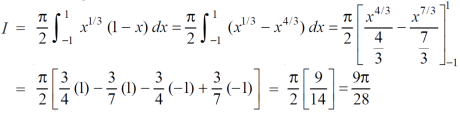
Question-11: Evaluate  ey/x dy dx.
ey/x dy dx.
Soln. :
Given : I = 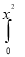 ey/x dy dx
ey/x dy dx
Here limits of inner integral are functions of y therefore integrate w.r.t y,
I =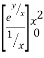
 dx
dx
= 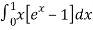
= 
I = 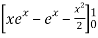
= =
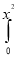 ey/x dy dx=
ey/x dy dx=
Question-12: Evaluate 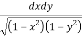
Soln. :
Let,I =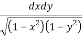
Here limits for both x and y are constants, the integral can be evaluated first w.r.t any of the variables x or y.
I = dy 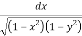
I= 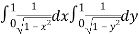
= 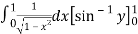
= 
= 
=
= 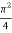
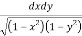 =
=
Question-13: Evaluate  over x 1, y
over x 1, y 
Soln. :
 Let I=
Let I=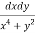 over x 1, y
over x 1, y 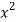
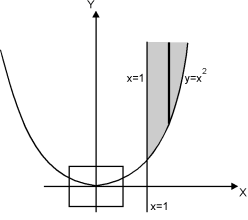
The region bounded by x 1 and y 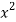
Is as shown in Fig. 6.3.
Fig. 6.3
Take a vertical strip along strip x constant and y varies from y = 
To y = . Now slide strip throughout region keeping parallel to y-axis. Therefore y constant and x varies from x = 1 to x = .
I= 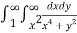
= 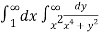
= 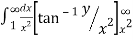 [ ∵
[ ∵ dx = tan–1 (x/a)]
dx = tan–1 (x/a)]
= 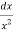 =
=
=– = (0 – 1)
I =
Question-14: Evaluate
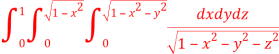
Solution: Let
I = 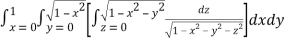
= 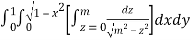
(Assuming m = 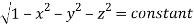 )
)
= 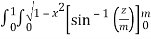 dxdy
dxdy
= 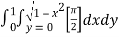
=
= 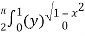 dx
dx
= 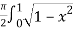 dx
dx
= 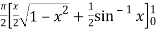
=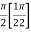
I =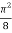
Question-15: Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane
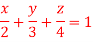
Solution: Volume =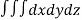 ………. (1)
………. (1)
Put 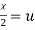 ,
, 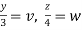

From equation (1) we have
V = 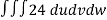
=24
=24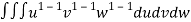 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 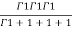
=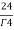 =
=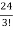 = 4
= 4
Volume =4
Question-16: Evaluate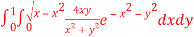
Soln. :
The region of integration bounded by
y = 0, y = 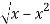 and x = 0, x = 1
and x = 0, x = 1
y =  x2 + y2 = x
x2 + y2 = x
The region bounded by these is as shown in Fig. 6.8.
Convert the integration in polar co-ordinates by using x = r cos , y = r sin and dx dy = r dr d
x2 + y2= x becomes r = cos
y = 0 becomes r sin = 0 = 0
x = 0 becomes r cos = 0 =
And x = 1 becomes r = sec
Take a radial strip SR with angular thickness , Along strip constant and r varies from r = 0 to r = cos . Turning strip throughout region therefore varies from = 0 to =
I =  r dr d
r dr d
= 4 cos sin d r  dr
dr
= 4 cos sin d [–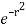 ]
]
= – 2 cos sin [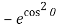 +1] d
+1] d
= – 2 [cos sin 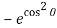 – cos sin ] d
– cos sin ] d
= –2 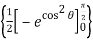 + 2 cos sin d
+ 2 cos sin d
= – + 2
= + 1 =
 Question-17: Sketch the area of double integration and evaluate
Question-17: Sketch the area of double integration and evaluate
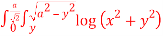 dxdy
dxdy
Soln. :
Let I = dxdy
dxdy
The region of integration is bounded by the curves
x = y, x = 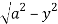 and y = 0, y = Fig. 6.9
and y = 0, y = Fig. 6.9
i.e. x = y, x2 + y2 = a2 and y = 0, y =
The region bounded by these is as shown in Fig. 6.9.
The point of intersection of x = y and x2 + y2 = a2 is x =
Convert given integration in polar co-ordinates by using polar transformation x = r cos , y = r sin and dx dy = r dr d
x = y gives r cos = r sin tan = 1 =
x2 + y2 = a2 r2 = a2 r = a
y = 0 gives r sin = 0 = 0.
y = gives r sin = r = cosec
Take a radial strip SR, along SR constant and r varies from r = 0 to r = a. Turning this strip throughout region therefore varies from = 0 to =
I = log r2 r dr d = 2 d r log r dr
I = 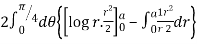
= 2 d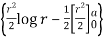
= 2 d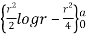
= 2 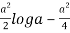 d
d
= 2 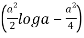 []
[]
I =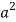 [/4] =
[/4] = 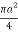
Question-18: Find the area between the curves 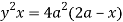 and its asymptote.
and its asymptote.
Solution: The curve is symmetrical about x axis not passing through origin. Also 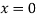 is the asymptote to the curve and intersect x axis at
is the asymptote to the curve and intersect x axis at  for
for 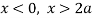 curve doesn’t exists. And for
curve doesn’t exists. And for  and
and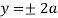 . Because of symmetry
. Because of symmetry

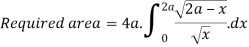
Put 
x | 0 | 2a |
t | 0 | 1 |
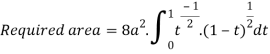
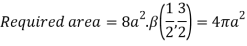
Question-19: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.
Sol. Let,
y ² = 4ax ………………..(1)
And
x² = 4ay…………………..(2)
Then if we solve these equations , we get the values of points where these two curves intersect
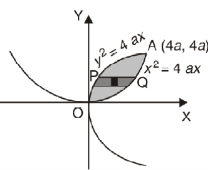
x varies from y²/4a to  and y varies from o to 4a,
and y varies from o to 4a,
Now using the conceot of double integral,
Area = 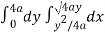
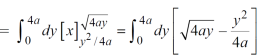
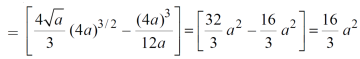
Question-20: Find the are lying inside a cardioid r = 1 + cos θ and ouside the parabola r(1 + cos θ) = 1.
Sol. Let,
r = 1 + cos θ ……………………..(1)
r(1 + cos θ) = 1……………………..(2)
Solving these equestions , we get
(1 + cos θ )( 1 + cos θ ) = 1
(1 + cos θ )² = 1
1 + cos θ = 1
Cos θ = 0
θ = ±π / 2
So that, limits of r are,
1 + cos θ and 1 / 1 + cos θ
The area can be founded as below,
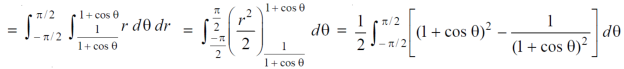
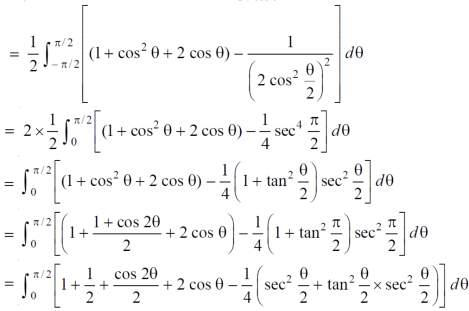

Question-21: Determine the coordinates of the centroid of the area lying between the curve y = 5x - x² and the x-axis.
Sol.
Here y = 5x - x² when y = 0, x = 0 or x = 5
Therefore the curve cuts the x-axis at 0 and 5 as in the figure-
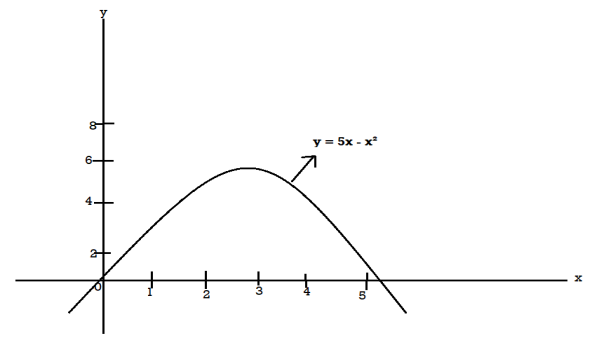

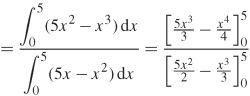
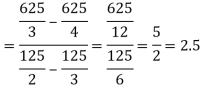
Now
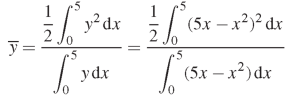
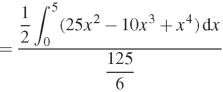
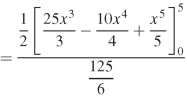
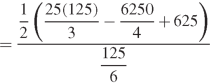
= 2.5
Therefore the centroid of the area lies at (2.5, 2.5)