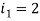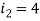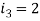UNIT-1
Matrix
Question Bank
Question-1: check whether the following matrix A is symmetric or not?
A = 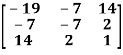
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,
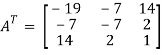
Here,
A = 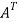
So that, the matrix A is symmetric.
Question-2: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
Sol. Suppose A is any square matrix .
Then,
A = 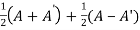
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Question-3: Express the matrix A as sum of hermitian and skew-hermitian matrix where 
Let A =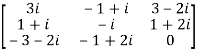
Therefore 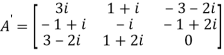 and
and 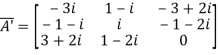
Let 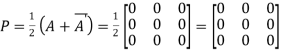
Again 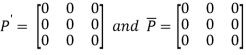
Hence P is a hermitian matrix.
Let 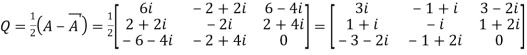
Again 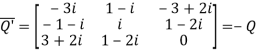
Hence Q is a skew- hermitian matrix.
We Check
P +Q=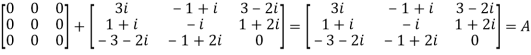
Hence proved.
Question-4: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA
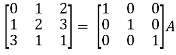
Apply  , we get
, we get
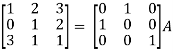
Apply 

Apply 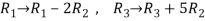
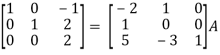
Apply 
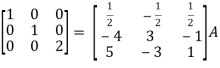
Apply 
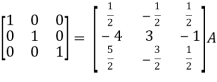
So that,
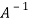 =
= 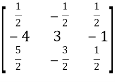
Question-5: Find the rank of a matrix M by echelon form.
M = 
Sol. First we will convert the matrix M into echelon form,
M = 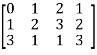
Apply, 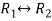 , we get
, we get
M = 
Apply  , we get
, we get
M = 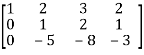
Apply 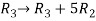
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Question-6: Find the rank of a matrix A by echelon form.
A = 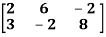
Sol. Transform the matrix A into ech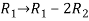 elon form, then find the rank,
elon form, then find the rank,
We have,
A = 
Apply, 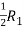
A = 
Apply 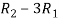 ,
,
A = 
Apply 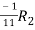
A = 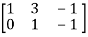
Apply 
A = 
Hence the rank of the matrix will be 2.
Question-7: reduce the matrix A to its normal form and find rank as well.


Sol. We have,

We will apply elementary row operation,
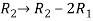
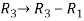
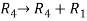
We get,

Now apply column transformation,

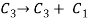
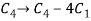
We get,

Apply
 , we get,
, we get,
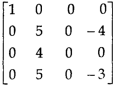
Apply 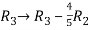 and
and 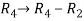

Apply 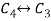

Apply 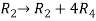 and
and 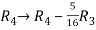

Apply 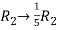 and
and 

As we can see this is required normal form of matrix A.
Therefore the rank of matrix A is 3.
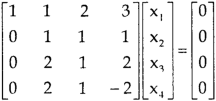
Question-8: Find the solution of the following homogeneous system of linear equations,
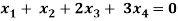
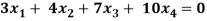
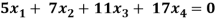

Sol. The given system of linear equations can be written in the form of matrix as follows,

Apply the elementary row transformation,

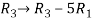
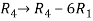 , we get,
, we get,
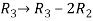
 , we get
, we get
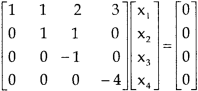
Here r(A) = 4, so that it has trivial solution,

Question-9: Check the consistency and find the values of x , y and z of the following system of linear equations.
2x + 3y + 4z = 11
X + 5y + 7z = 15
3x + 11y + 13z = 25
Sol. Re-write the system of equations in augmented matrix form.
C = [A,B]
That will be,
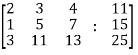
Apply 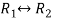

Now apply , 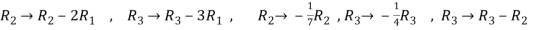
We get,
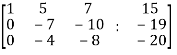 ~
~  ~
~ 
Here rank of A = 3
And rank of C = 3, so that the system of equations is consistent,
So that we can can solve the equations as below,

That gives,
x + 5y + 7z = 15 ……………..(1)
y + 10z/7 = 19/7 ………………(2)
4z/7 = 16/7 ………………….(3)
From eq. (3)
z = 4,
From 2,
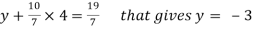
From eq.(1), we get
x + 5(-3) + 7(4) = 15
That gives,
x = 2
Therefore the values of x , y , z are 2 , -3 , 4 respectively.
Question-10: Test the consistency of the following set of equations.
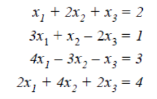
Sol. We can write the set of equations in matrix form :
-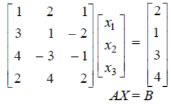
We have augmented matrix C = [A:B]
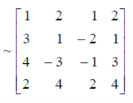
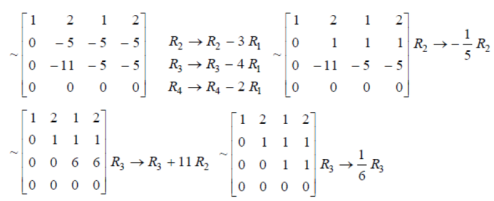
Here we know that,
Number of non-zero rows = Rank of matrix
R(C) = R(A) = 3
Hence the given system is consistent and has unique solution.
Question-11: Find the characteristic equation of the matrix A:
A = 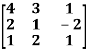
Sol. The characteristic equation will be-
|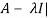 = 0
= 0
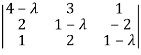 = 0
= 0
On solving the determinant, we get
(4-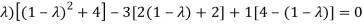
Or 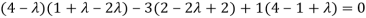
On solving we get,
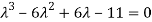
Which is the characteristic equation of matrix A.
Question-12: Find the characteristic equation and characteristic roots of the matrix A:
A = 
Sol. We know that the characteristic equation of the matrix A will be-
|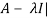 = 0
= 0
So that matrix A becomes,
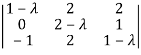 = 0
= 0
Which gives , on solving
(1- = 0
= 0
Or 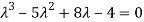
Or (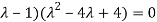
Which is the characteristic equation of matrix A.
The characteristic roots will be,
( (
(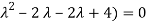
(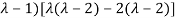
(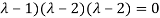
Values of 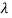 are-
are-
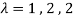
These are the characteristic roots of matrix A.
Question-13: Find out the Eigen values and Eigen vectors of  ?
?
Sol. The Characteristics equation is given by 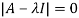

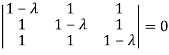
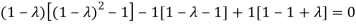
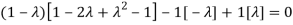
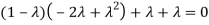
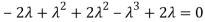
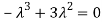

Or 
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 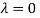 is
is
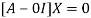
Where X is the column matrix of order 3 i.e.
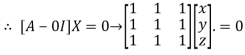
This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1)=2 linearly independent solutions.
Let 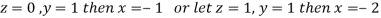
Thus the Eigen vectors corresponding to the Eigen value  are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value  is
is
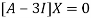
Where X is the column matrix of order 3 i.e.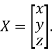
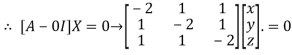
This implies that 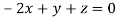
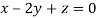
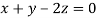
Taking last two equations we get
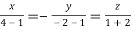
Or 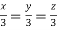
Thus the Eigen vectors corresponding to the Eigen value 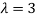 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Question-14: Verify the Cayley-Hamilton theorem and find the inverse.
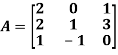
Sol. The characteristics equation of A is 
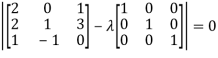
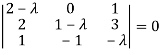
Or 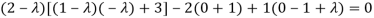
Or 
Or 
Or 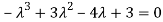
Or 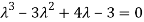
By Cayley-Hamilton theorem 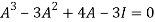
L.H.S. 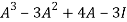
=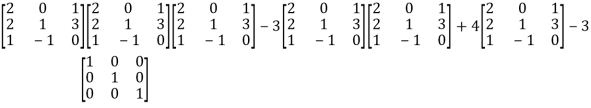
=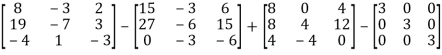
=
Multiply both side with  in
in 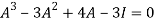

Or 
Or 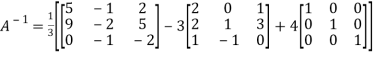
=
Question-15: Verify Cayley-Hamilton theorem for matrix A:
A = 
Sol. Characteristic equation of matrix A will be, 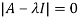
 = 0
= 0
(2-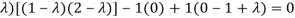
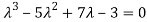
According to Cayley-Hamilton theorem,
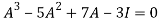 …………..(1)
…………..(1)
Here we need to verify eq.(1)-
First we will find A² -
A² = 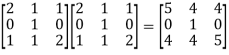
Now,
A³ = A².A = 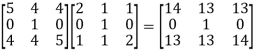
Equation (1) becomes,
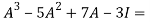
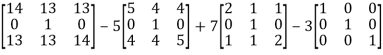
= 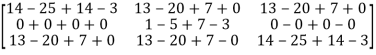
= 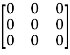
Hence the Cayley-Hamilton theorem is verified.
Question-16: Find the currents 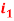 ,
, 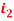 ,
,  in the following electric circuit.
in the following electric circuit.
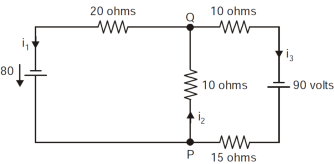
Sol. In order to find out the result first we will go through Kirchoff’s current law and voltage law –
Kirchoff’s current law- The sum of the in flowing currents equals to the sum of the out flowing currents at any points of the circuit.
Kirchoff’s voltage law- The sum of all voltages drops equals the impressed electromotive force in a closed loop.
Node P gives- 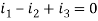
Node Q gives- 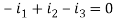
Right loop gives- 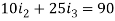
Left loop gives- 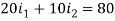
We have these four equations.
Let’s solve these equations by matrix method-
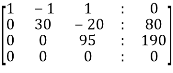
The augmented matrix will be-
[A : B] = 
Apply 

Apply 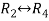

Apply 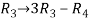
Apply 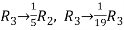

Now we get-

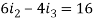
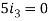
On solving these, we get-