UNIT- 2
Differential Calculus-I
Question Bank
Question-1: Find nth derivative of log(ax + b)
Sol.
Suppose y = log (ax + b)
Differentiate with respect to x successively, we get
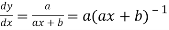
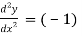
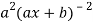
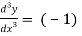 (-2)
(-2) 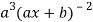
.
.
.
For n times differentiation, we get-
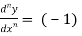 (-2)…………….(-n + 1)
(-2)…………….(-n + 1) 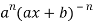
= 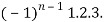 …………….(n - 1)
…………….(n - 1) 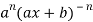
= 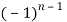 (n - 1)
(n - 1)
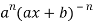
So we can say that its n’th derivative will be
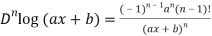
Question-2: Find the 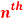 derivative of the following function-
derivative of the following function-
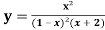
Sol. Partial fraction of the function y after splitting-
Suppose x – 1 = z, then
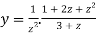
= 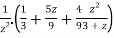
= 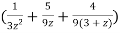
= 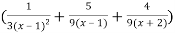
Here we can find its n’th derivative-
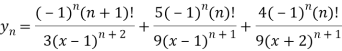
Question-3: Find 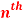 derivative of the given function:
derivative of the given function:
y = 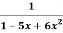
Sol. We are given-
y = 
factorize the denominator-
y = 
= 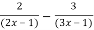
 derivative will be-
derivative will be-
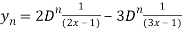
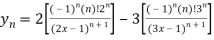
Which is the  derivative of the given function.
derivative of the given function.
Question-4: If y 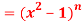 , then prove that-
, then prove that-
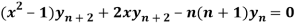
Sol. Here it is given that-
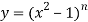
On differentiating-
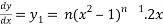
Or
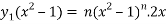
= ny.2x
Differentiate again with respect to x, we get-
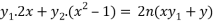
Or
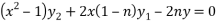 …………………. (1)
…………………. (1)
Differentiate each term of (1) by using Leibnitz’s theorem, we get-
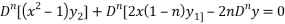

Therefore we get-

Hence proved.
Question-5: If 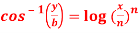 , then prove that-
, then prove that-
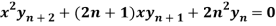
Sol. Here we have-
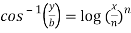
Or

Or
y = b cos[ n log(x/n)]
On differentiating, we get-
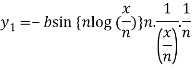
Which becomes-

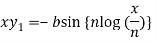
Differentiate again both sides with respect to x, we get-

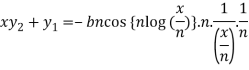
It becomes-

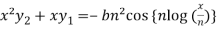

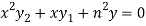 ……………….. (1)
……………….. (1)
Differentiate each term n times with respect to x, we get-
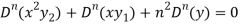

Which is-
 hence proved
hence proved
Question-6: Calculate 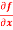 and
and  for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate 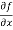 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
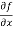 =
= 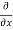 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 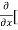 3x³] -
3x³] - 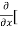 5y²] +
5y²] +  [2xy] -
[2xy] - 8x] +
8x] + 4y] -
4y] -  20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
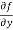 =
= 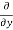 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 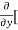 3x³] -
3x³] - 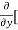 5y²] +
5y²] + 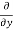 [2xy] -
[2xy] -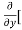 8x] +
8x] +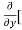 4y] -
4y] -  20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Question-7: Calculate 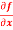 and
and  for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Sol. To calculate  treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
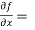
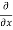 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)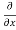 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50) cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,

 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8) (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Question-8: if 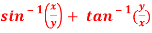 , then show that-
, then show that- 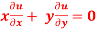
Sol. Here we have,
u =  …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get

= 
Or
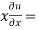
 ………………..(2)
………………..(2)
And now,

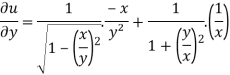
= 
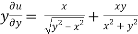 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get

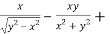
 = 0
= 0
Hence proved.
Question-9: If u = x²(y-x) + y²(x-y), then show that 
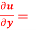 -2 (x – y)²
-2 (x – y)²
Solution - here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
now differentiate u partially with respect to x and y respectively,
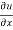 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
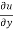 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
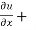
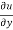 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Question-10: If  then prove that
then prove that
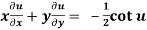
Sol. Here, given-
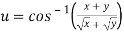
Here u is not a homogeneous function but z =
cos u, then
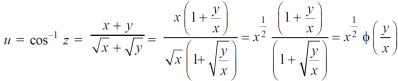
Now z is a homogeneous function in x, y of degree 1 / 2.
Now by Euler’s theorem-
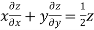
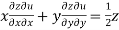

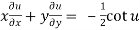
Question-11: If 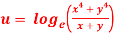 then show that-
then show that-
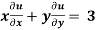
Sol. Here we have-
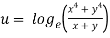
u is not homogenous function here but,
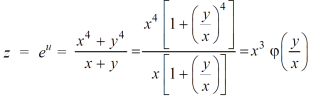
Here z is a function of degree 3.
By using Euler’s deduction formula, we get-
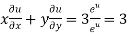
So that
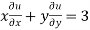
Question-12: If u = u then show that
then show that 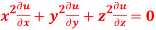
Sol. Here it is given that,
u = u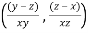 = u(r , s)
= u(r , s)
Where r = 
Which gives-
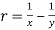 and
and …………………. (1)
…………………. (1)
Now, we know that-
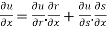
=
= 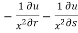
Or
 ……………….. (2)
……………….. (2)
Similarly-
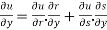

Or

And-
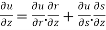

Adding the results, we get
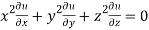
Question-13: Find the horizontal asymptote of the function-
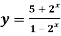
Sol. Find the limits-

And
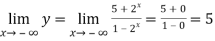
Hence the horizontal asymptotes are y = -1 and y = 5.
Figure will be as follows of the asymptotes of the given function-

Question-14: Find the slant asymptotes of 
Sol. We have,
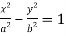
Which can be written as-

The value of ‘m’ will be-
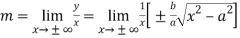
= 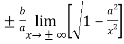 =
= 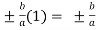
Now we can find ‘c’ as –
c =  =
= 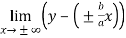 =
= 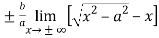
= 0
Hence the slant asymptotes are 
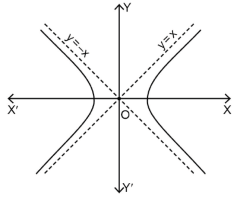
Question-15: Trace the curve y = 1/x².
Sol. As we can see y- coordinates of the curve can not be negative. So the curve must be above x-axis. The curve is also symmetric about y-axis so we can draw the graph only in single side.
Here, we will find the first and second derivatives-
So, dy/dx= -2/x³ and d²y/dx² = 6/ x⁴ , here dy/dx <0 for all x>0 so we can say that the function is non- increasing so the graph falls as we increase x.
Also second derivative is also non zero so there are no point of inflection.
Here the curve is x²y=1 (rewritten), here both the axes are asymptotes of the curve.
Here is the figure of the curve-:
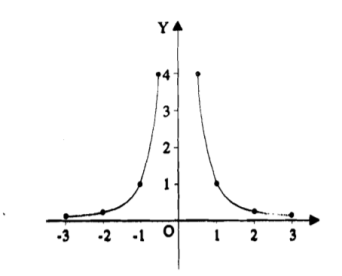
Question-16: Trace the curve 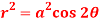 .
.
Sol. Symmetry about initial line- Put r = 0, 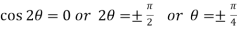
Hence the straight line 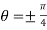 are the tangents to the curve at the pole.
are the tangents to the curve at the pole.
Values of ‘r’ as  changes from 0 to π-
changes from 0 to π-
Table for the values of ‘r’-
 | 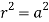 |  |
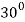 |  |  |
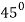 | 0 | 0 |
 |  | Imaginary |
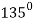 | 0 | 0 |
 |
 |  |
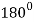 |
 | 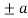 |
Here according to the table the curve does not exist for the value lying between 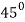 to
to 
The figure will be as follows of the curve-
