UNIT- 3

Differential Calculus-II

Question Bank

Question-1: Expand f(x , y) = 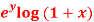in powers of x and y about origin.

Sol. Here we have the function-

                                               f(x , y) =

Here , a = 0 and b = 0 then

                                             f(0 , 0) =

Now we will find partial derivatives of the function-

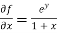
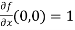
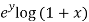
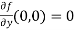
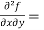
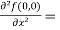
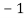
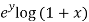
Now using Taylor’s theorem-

+………

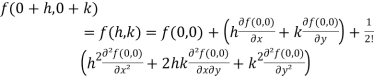Suppose h = x and k = y , we get

+…….

             = +……….

Question-2: Calculate log [ 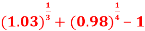]approximately by using Taylor’s expansion.

Sol.  Suppose-   f(x , y) = log [ ]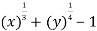

                             f(1 , 1) = log 1 = 0

Now we will find out the derivatives- take a = 1 and b = 1

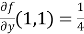
Using Taylor’s theorem-

+ ……………….

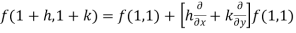But here,

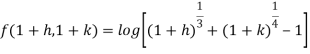
So that-

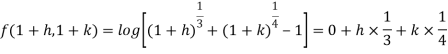
Put h = 0.03 and k = -0.02 , we get

Question-3: Expand sin x in powers of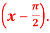

Sol. Let f(x) = sin x

     Then,

                    =

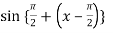
          By using Taylor’s theorem-

         + …….     (1)

Here f(x) = sin x and a = π/2

f’(x) = cos x  , f’’(x) = - sin x    ,     f’’’(x) = - cos x  and so on.

Putting x = π/2 , we get

f(x) = sin x = 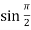= 1

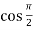f’(x) = cos x = = 0

f’’(x) = -sin x = 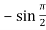= -1

f’’’(x) = -cos x = = 0

From equation (1) put a = and substitute these values, we get-

+ …….    

         = ………………………..

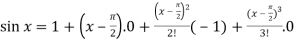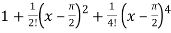Question-4: If x = r sin , y = r sin , z = r cos, then show that

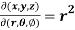                      sin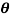  also find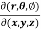 

Sol.  We know that,

                                       =

                                       =

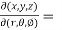
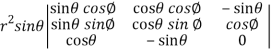
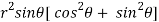                                       =      ( on solving the determinant)

                                      = 

Now using first propert of Jacobians, we get

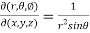
Question-5: If u = xyz , v = x² + y² + z²  and w = x + y + z, then find   J = 

Sol. Here u ,v and w are explicitly given , so that first we calculate

                              J’ =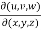

                             J’ =   =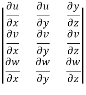

  = yz(2y-2z) – zx(2x – 2z) + xy (2x – 2y) = 2[yz(y-z)-zx(x-z)+xy(x-y)]

  = 2[x²y - x²z - xy² + xz² + y²z - yz²]

  = 2[x²(y-z)  - x(y² - z²) + yz (y – z)]

  = 2(y – z)(z – x)(y – x)

  = -2(x – y)(y – z)(z – x)

By the property,

                            JJ’ =  1

                         J =

Question-6: If u = 2axy, v = then prove that-

Sol. Here we have,

                                     u = 2axy, v =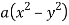    

      Then

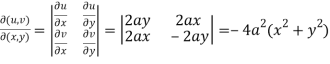
    Here -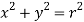 

    So that

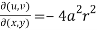
Now,

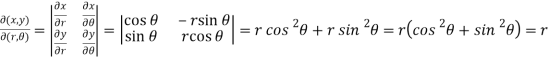
Hence-

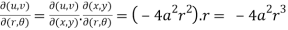
                      Hence proved.

Question-7: Show that 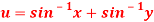and 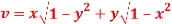are functionally dependent.

Sol. Here we have-

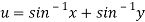                              and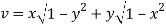   

Now we will find out the Jacobian to check the functional dependence.

                        =

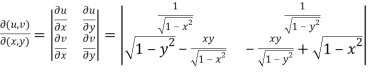
Here Jacobian is zero, so we can conclude that these functions are functionally dependent.

Question-8: Find out the maxima and minima of the function

Sol.   Given 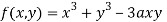    …(i)

         Partially differentiating (i) with respect to x we get

                   ….(ii)

         Partially differentiating (i) with respect to y we get

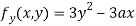                    ….(iii)

          Now, form the equations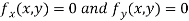

                    Using (ii) and (iii) we get

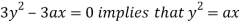
                                  using above two equations

                     Squaring both side we get

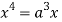
                      Or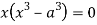 

                       This show that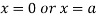

                         Also we get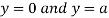

                 Thus we get the pair of value as

                  Now, we calculate

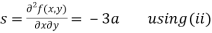
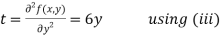
      Putting above values in

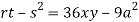
      At point (0,0)  we get

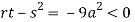
      So, the point (0,0) is a saddle point.

      At point 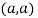we get

        So the point 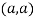is the minimum point where

          In case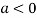 

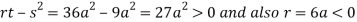
         So the point is the maximum point where

Question-9: There is rectangular box which is open at the top, is to have a volume of 32 c.c.

Find the dimensions of the box requiring least (minimum) material to construct it.

Sol. Here it is given that-

                                       Volume (V) = 32 c.c.

Suppose ‘l’ , ‘b’, ‘h’ are the length, breadth, height of the rectangular box respectively and its surface area is ‘S’.

As we know that-

                                Volume (V) = l b h = 32

                                b (breadth) = 32/lh

And the surface area of the rectangular box which is open at the top is-

                               S = 2 (l + b) h + l b   …………… (1)

On putting the value of ‘b’ in (1), we get-

                               S = 2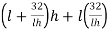

                                S = 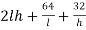        ……………… (2)

Differentiate partially equation (2) with respect to l and h respectively, we get-

                …………… (3)  and     …………….. (4)

For Max. And Min. S, we get-

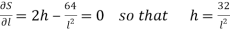
And     

The values of ‘l’, ‘h’ and ‘b’ will be-

L = 4, h = 2 and b = 4

Now-

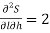
And

So that-

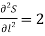, then S is minimum for l = 4, b = 4, and h = 2

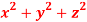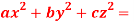Question-10: Determine the maxima and minima of when                                           1

Sol. Suppose    ……….. (1)

And 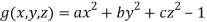=0  …………… (2)

Differentiate partially equation (1) and (2) w.r.t. x and y respectively, we get-

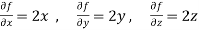
And                            

Now using Lagranges’s equations, we get-

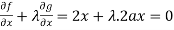
Which gives-

                                                                or 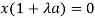          ……… (3)

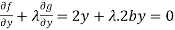
Which gives-

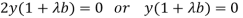                                                            …… (4)   

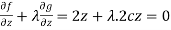
Which gives-

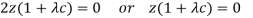                                                 ……. (5)

Multiply these equations by x, y, z respectively and adding, we get-

                                     (

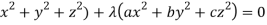
Hence we get-

                             f + 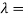0   then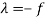 

Put 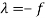in (3) , (4) and (5), we get-

x(1 – fa) = 0   ,   y(1 – fb) = 0 and z(1 – fc) = 0

We get-

These gives the maximum and minimum values of f.

Question-11: Find the volume of the largest rectangular parallelepiped which can be inscribed in the ellipsoid 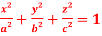by using method of Lagranges’s multipliers.

Sol. We have-

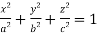
Let 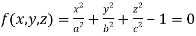                                           ……………. (1)

Suppose 2x , 2y and 2z are the l , b and h of the rectangular parallelepiped inscribed in the ellipsoid.

Then the volume will be-

                                           V = (2x)(2y)(2z) = 8 xyz  ……………… (2)

Differentiate equation (1) and (2) partially with respect to x and y respectively, we get-

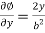
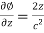
And

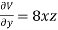
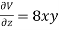
Now, Lagrange’s equations are-

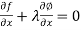
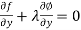
So that,

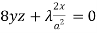                                            …………… (3)

                                          ………………. (4)

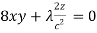                                         ……………………… (5)

Multiply (3), (4) and (5) by x, y, z and adding, we get-

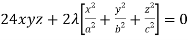
As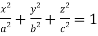 

Then,

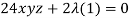
                                         2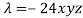

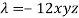
Putting the value of in equation (3), (4), and (5), we get-

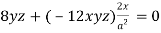  gives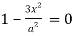        

Which gives-

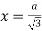
Now put in (4)-

Similarly,

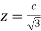
So that the volume of the largest rectangular parallelepiped = 8xyz

                                  = 8 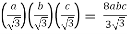                    Ans.