UNIT-4

Multiple Integrals

Question-1: Evaluate 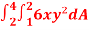, where dA is the small area in xy-plane.

Sol.     Let,   

I =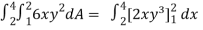 

=

= 

= 

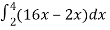
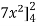
=    84 sq. Unit.

Which is the required area.

Question-2: Evaluate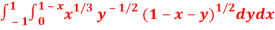

Sol. Let us suppose the integral is I,

                            I =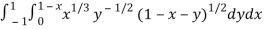

Put c = 1 – x in I, we get

                           I =

Suppose, y = ct

Then dy = c

Now we get,

I =

I =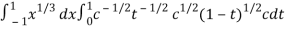

I =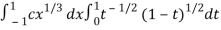

I =

I  =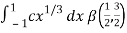

           As we know that by beta function,

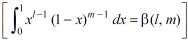
         Which gives,

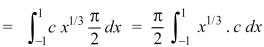
Now put the value of c, we get

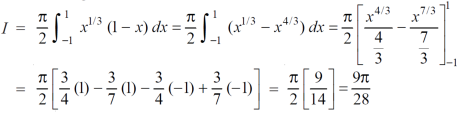
Question-3: Evaluate 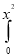 ey/x dy dx.

Soln. :

Given : I = ey/x dy dx

Here limits of inner integral are functions of y therefore integrate w.r.t y,

I = 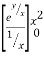dx

                                     =            

                                    =

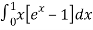
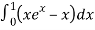
I =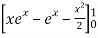

                                    =            =

ey/x dy dx=

Question-4: Evaluate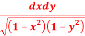

Soln.:

Let,I =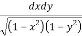

Here limits for both x and y are constants, the integral can be evaluated first w.r.t any of the variables x or y.

I = dy 

I=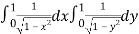

                                     =          

=          

                                     =          

                                     = 

                                    =

=

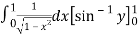
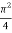
Question-5: Evaluate

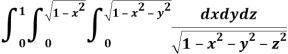
Solution:

Let

     I     =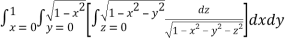    

            =    

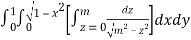
                                            (Assuming m = )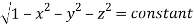

             = dxdy

           =

             =

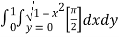
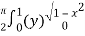           = dx

           =  dx

           = 

           =

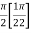
         I =

Question-6:Evaluate

Solution:-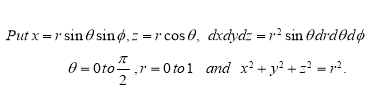

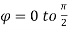
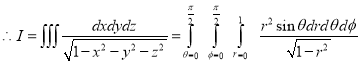
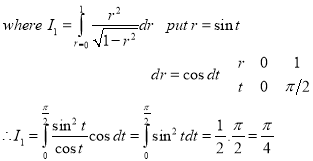
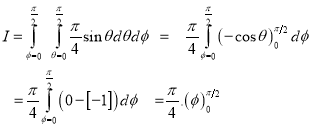
Question-7: Find volume common to the cylinders, .

Solution:    For given cylinders,

,    .

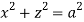   Z varies from

                     Z=-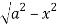   to  z =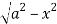

Y varies from

                        y= -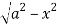   to  y =

x varies from   x= -a to x = a

By symmetry,

Required volume= 8 (volume in the first octant)

                                 =8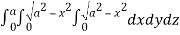

                                 =8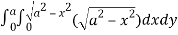

                                  = 8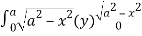dx

                                  =8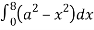

                                  =8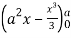

                                   =8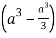

                 Volume   =   16

Question-8: Change the order of integration in the double integral-

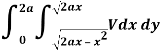
Sol.

Limits are given-

x = 0, x = 2a

And

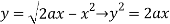
And

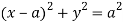
The area of integration is the shaded portion of OAB. On changing the order of integration first we will integrate with respect to x, the area of integration has three portions BCE, ODE and ACD,

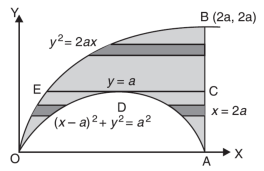
Now-

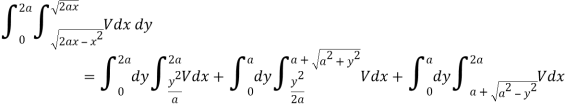
Which is the required answer.

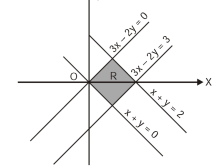
Question-9: Evaluate-

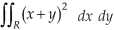
Where-

R is the region bounded by a parallelogram- x + y = 0, x + y = 2, 3x – 2y = 0, 3x – 2y = 3.

Sol.

By changing the variables x, y to the new variables u and v, by the substitution x + y = u, 3x – 2y = v, the given parallelolgram R reduces to a rectangle

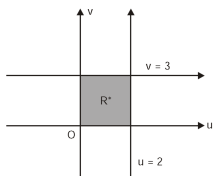
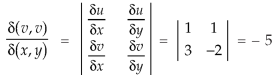
The required Jacobian is-

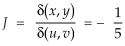
Since u = x + y and  u = x + y = 2, here u varies from 0 to 2 while v varies from 0 to 3.

Since-

3x – 2y = v = 0, 3x – 2y = v = 3

Therefore the integral will be in new variables-

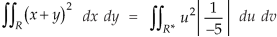
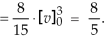
Which is the required answer.

Question-10: Evaluate 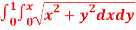the transformation is x = v and y = uv.

Sol.

Here the region of integration R is the triangle which is bounded by y = 0, x = 1 and y = x

Here put,

X = u and y = uv, we get-

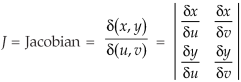
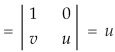
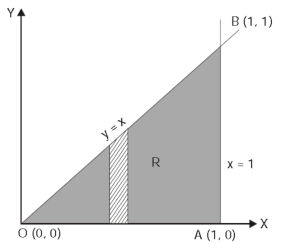
Here x varies from 0 to 1 while y varies from 0 to x.

Since u = x so u varies from 0 to 1

Here, similarly, since 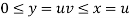, so that v varies from 0 to 1. Thus-

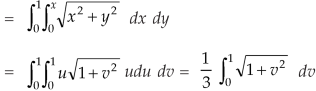
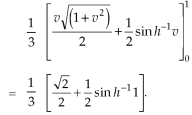
Question-11: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.

Sol. Let,

y ² = 4ax ………………..(1)

And

x² = 4ay…………………..(2)

Then if we solve these equations , w e get the values of points where these two curves intersect

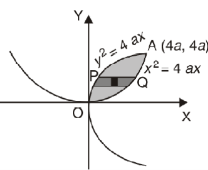
x varies from y²/4a to and y varies from o to 4a,

Now using the conceot of double integral,

                    Area =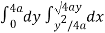 

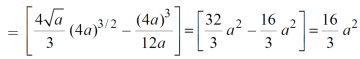
Question-12: Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane

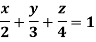
Solution: Volume =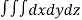                                                 ………. (1)   

                Put          ,  

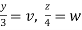
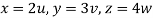
  From     equation (1) we have

   V =

        =24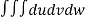

         =24           (u+v+w=1) By Dirichlet’s theorem.

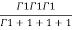
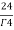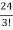         =24

         =  = = 4

Volume =4

Question-13: Evaluate 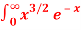dx

Solution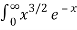 dx = dx

= γ(5/2)

         = γ (3/2+ 1) 

         = 3/2 γ(3/2 )  

        = 3/2.  ½ γ (½ ) 

= 3/2. ½ π 

        =    ¾ π  

Question-14: Evaluate  dx.

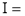
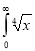
Solution: Let   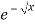 dx 

X	0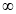
t	0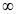

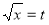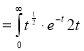                                                    Put or ;dx =2t dt .

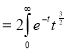dt

dt

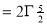
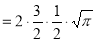
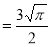
Question-15: Evaluate the integral-

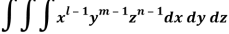
Where x, y and z are positive with conditions-

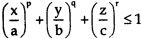
Sol. Let us put-

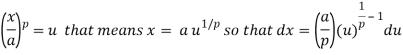
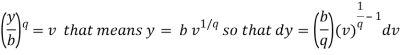
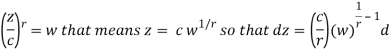
So that the required integral will be-

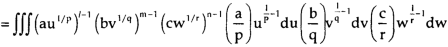
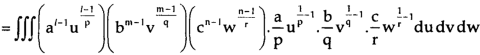
Where u + v + w ≤ 1

By Dirichlet’s integral-

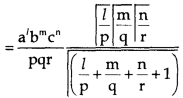
Question-16: Show that-

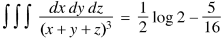
The conditions are given x + y = 0, y = 0, z = 0, x + y + z = 1.

Sol.

By Lioville’s theorem when 0 < x + y + z < 1 

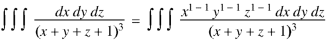
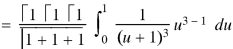
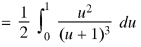
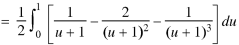
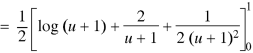
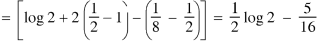
Proved.