Section B
Transformers
Question Bank
Q1. A 2500/200 V transformer draws a no-load primary current of 0.5 A and absorbs 400 W. Find magnetising and loss currents.
Sol: Iron-loss current = No load input(W) / Primary voltage
= 400/2500 = 0.16 A
I20 = I2w + I2µ
Iµ = √I20 – I2w
= √ (0.5)2 – (0.16)2
Iµ = 0.473 A
Q2. A 1-φ transformer has 1000 turns on primary and 200 on secondary. The no load current is 4 amp at p.f of 0.2 lagging. Find primary current and pf when secondary current is 280 A at pf of 0.6 lagging.
Sol : cos-1 0.6 = 53.130 (sin φ = 0.8)
I2 = 280/-53.130A
Φ = cos-1 0.2 = 78.50
Sin φ = 0.98
I1 = I0 + I’2
I’2 = (I2/K) ( -53.130
K = N1/N2 = 1000/200 = 5
I’2 = 280/5 (-53.130
I’2 = 56(-53.130
I1 = I0 + I’2
= 4(0.20 – j0.98) + 56(0.6 – j0.8)
= 0.80 – j3.92 + 33.6 – j44.8
I1 = 34.4 – j48.72
I1 = 59.64 ( -54.770
I lag supply voltage by 54.770
Q3) A 1- φ transformer with ratio of 440/110-V takes a no-load current of 6 A at 0.3 pf lagging. If secondary supplies 120 A at pf of 0.8 lagging. Find current taken by primary.
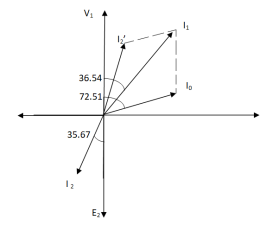
Sol>.
Cos φ2 = 0.8
Φ2 = 36.540
Cos φ0 = 0.3
Φ0 = 72.540
K = V2/V1 = 110/440 = ¼
I’2 = KI2 = 120 x ¼ = 30 A
I0 = 6A
Angle between I0 & I’2
= 72.54 – 36.54
= 35.670
From vector diagram,
I1 = √(62 + 302 + 2 x 6 x 30 cos 35.67)
I1 = 35.05 A
Q4) A – 100 KVA transformer has 500 turns on primary and 80 turns on secondary. The primary and secondary resistances are 0.3 and 0.01 Ω respectively and the corresponding leakage reactance’s are 1.1 and 0.035 Ω. The supply voltage is 2400 V. Find
(I). Equivalent impedance referred to primary
(ii). Voltage regulation and the secondary terminal voltage for full load having pf 0.8 lagging?
Sol. Equivalent impedance referred to primary
Z01 = √R201 + X201 = R01 + jX01
R01 = R1 + R2/K2 = 0.3 + 0.01/K2 = 0.69 Ω
K = 80/500 = 4/25
X01 = X1 + X2/K2 = 1.1 + 0.035/(0.16)2 = 2.467 Ω
Z01 = 0.69 + j2.46
(ii). Secondary terminal voltage Z02 = K2 Z01
Z02 = 0.018 + j 0.063
= 0.065 ( 74.050
No-load secondary voltage = KV1
= 0.16 x 2400 = 384 V
I2 = 100 x 103/384 = 260.42 A
Full load voltage drop referred to secondary
= I2 (R02 cosφ – X02 Sinφ)
Cosφ = 0.8
Φ = 36.860
Sinφ = 0.6
= 260.42(0.018 x 0.8 – 0.063 x 0.6)
= - 6.094 V
% regn = -6.094/384 x 100
= -1.587
Secondary terminal voltage on-load
= 384 – (-6.094)
= 390.09 V
Q5) In a 50 KVA, 2200/200 V, 1-φ transformer, the iron and full-load copper losses are 400 W and 450 W respectively. Calculate n at unity power factor on (I). Full load (ii). Half-full load?
Sol. (I). Total loss = 400 + 450 = 850 W
F.L output at unity power factor = 50 x 1
= 50 KVA
n = 50 / 50 + .850 = 50/50.850 = 0.98 = 98%
(ii). Half full load, unity pf
= 50 KVA/2 = 25 KVA
Cu loss = 400 x (1/2)2 = 100 W
Iron loss is same = 450 W
Total loss = 100 + 450 = 550 W
n = 25/25 + 0.55 = 25/25.55 = 0.978 = 97.8 %
Q6) A 40 KVA 440/220 V, 1- φ, 50 Hz transformer has iron loss of 300 W. The cu loss is found to be 100 W when delivering half full-load current. Determine (I) n when delivering full load current at 0.8 lagging pf (ii) the percentage of full-load when the efficiency will be max.
Sol. Full load efficiency at 0.8 pf
= 40 x 0.8/(40 x 0.8) + losses
Full load cu loss = (440/220)2 x 100
= 400 W
Iron loss = 400 + 300
= 700 W
n = 40 x 0.8/(40 x 0.8) + 0.7 = 97.8 %
(ii). KVA for maximum / F.L KVA = √ iron loss / F.L cu loss
= √300/400 = 0.866
Q7) An auto transformer suppliers load of 4KW at 100v at unity pf. IF the applied primary voltage is 220v. Calculating power transferred to load (a) Inductively (b) conductively.
Soln, Power transferred inductively = Input(1-k)
Power transferred conductively = K* Input
K=  =
=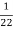
Input= Output =4KW
Inductively transferred power =4(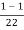 )
)
=3.82KW
Conductively transferred power = 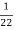 *4
*4
= 0.182 kw
Q8) The core of a 110 KVA, 10,000/500v, 50 Hz, 1-Φ core type transformer has a cross section of 18 cm x 18 cm. Find the number of HV and LV turns per phase and the emf per turn if the maximum core density does not exceed 1.3 tesla. Assume a stacking factor pf 0.9.
Sol: Bm= 1.3T
Area = (0.18 x 0.18) = 0.032m2
Emf induced in primary
E1 = 4.44 fN1BmA
10000=4.44 x 50 x N1 x 1.3 x 0.032
N1=1082.8
Emf induced in secondary
E2 = 4.44 fN2BmA
500= 4.44 x 50 x N2 x 1.3 x 0.032
N2= 54.14
i) The number of turns is N1=1082.8 and N2= 54.14
Ii) Emf per turn = E1/E2 = N1/N2 = K
=10000/1082=9.24V or 500/54.14=9.23V
Q9) A 1-Φ transformer has 400 turns in primary and 110 turns in the secondary. The cross-sectional area of the secondary. The cross-sectional area of the core is 80cm2. If the primary winding is connected to the 50 Hz supply at 500V. Calculate peak flux density in core.
Sol: As we know Emf induced in primary
E1 = 4.44 fN1BmA
500 = 4.44 x 50 x 400 x Bm x (80x10‑4)
Bm=0.704Wb/m2
Q10) A 2000/200v transformer draws a no-load primary current of 0.6A and absorbs 360 watts find the magnetising and iron loss currents.
Sol: Iron loss current =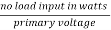 = 360/2000=0.18A
= 360/2000=0.18A
I20 = I2w + I2µ
Magnetising component Iµ = √I20 – I2w
= √ (0.6)2 – (0.18)2
Iµ = 0.57 A
Q.11) A 2200/250 V transformer takes 0.7A at a p.f of 0.4 0n open circuit. Find the magnetising and working component of no load primary current?
Sol: I0= 0.7A
Cosφ0=0.4
Iw= I0 cosφ0
Iw=0.7 x 0.4=0.28A
Magnetising component Iµ = √I20 – I2w
= √ (0.7)2 – (0.280)2
Iµ = 0.64 A
Q.12) A single phase transformer has 400 turns in primary and 1000 turns in secondary. The cross-sectional area is 80 cm2. If primary is connected to 50hz at 500V. Voltage induced in secondary?
Sol: As we know Emf induced in primary
E1 = 4.44 fN1BmA
500= 4.44x50x1000xBmx(80x10-4)
Bm= 0.28Wb/m2
The voltage induced in secondary is given as
E1/E2 = N1/N2 = K
E2=1000x500/400=1250V
Q.13) A 200 KVA, 1200/200v, 50 Hz, 1-Φ transformer has a leakage impedance of (0.1 + 0.30) Ω for the HV winding and (0.005 + 0.015) Ω for the LV winding. Find the equivalent winding resistance, reactance and impedance referred to the HV and LV side.
Sol: The Turn ratio is given as E1/E2 = N1/N2 = K
K=6
i) Referring to High Voltage Side
Resistance = R1+K2R2= 0.1+ 62 x 0.005 =0.28ohm
Reactance = X1+K2X2= 0.30+ 62 x0.015 = 0.84ohm
Impedance = √0.282 +0.842
=0.880hm
Ii) Referring to Low voltage sides
Resistance= R1/ K2+R2= (0.1/62) + 0.005=0.007ohm
Reactance = Reactance HV side/ K2=0.84/62=0.013ohm
Impedance = Impedance referring HV/ K2= 0.88/62 = 0.024ohm
Q14) When a transformer is connected to a 1200v,50Hz supply the core loss is 900 W, of which 600 is hysteresis and 350 W is eddy current loss. If the applied voltage is raised to 2000V and frequency to 100 Hz. Find new core losses.
Sol: Hysteresis Loss (Wh) α 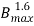 f =P
f =P 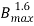 f
f
Eddy current Loss (We) α P f2 = Q
f2 = Q 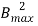 f
f
The emf equation of transformer is given as E= 4.44fNBmaxA
Bmax α E/f
So, the above equations become Wh = P (E/f)2 f = P E1.6 f-0.6
600= P x 12001.6 x 50-0.6
P=0.074
The eddy current loss We= Q (E/f)2 f2 = QE2
350=Q x 12002
Q=0.243 x 10-3
Now the applied voltage is raised to 2000V so finding new losses with above found P and Q
Wh = P E1.6 f-0.6 = 0.074 x 20001.6 x 100-0.6 = 893.06W
We= QE2 = 0.243 x 10-3 x 20002 = 972 W
Polyphase Circuits
Q15) Three identical impedances are connected in delta 3-phase supply of 400V. The line current is 30A and total power taken from the supply is 10kW. Calculate the resistance and reactance value of each impedance?
Sol: VL=Vph=400V
IL=30A
Iph=IL/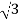 = 30/
= 30/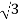 =17.32A
=17.32A
Zph=Vph/Iph= 400/17.32=23.09ohm
P=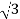 VLIL Cos Ø
VLIL Cos Ø
Cos Ø = 10000/ 400x30 = 0.48
400x30 = 0.48
Sin Ø =0.88
Rph=Zph Cos Ø= 23.09x0.48=11.08ohm
Xph=Zph Sin Ø = 23.09x0.88=20.32ohm
Q16) A star connected alternator supplies a delta connected load. The impedance of the load branch is 6+j5 ohm/phase. The line voltage is 230V. Determine the current in the load branch and power consumed by the load.
Sol: Zph= = 7.8ohm
= 7.8ohm
VL=Vph=230V
Iph=Vph/Zph=230/7.8=29.49A
Iph=IL/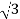
IL= 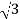 Iph=
Iph=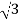 x29.49=51.07A
x29.49=51.07A
P=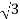 VLIL Cos Ø =
VLIL Cos Ø =  x 230x51.07x0.768=15.62kW
x 230x51.07x0.768=15.62kW
Q17) The load connected to a 3-phase supply comprise three similar coils connected in star. The line currents are 25A and the kVA and kW inputs are 18 and 10 respectively. Find the line and phase voltage, the kVAR input resistance and reactance of each coil?
Sol: IL= 25A
P= 10000W
Cos Ø = 10/18 = 0.56
P= VLIL Cos Ø
VLIL Cos Ø
10000= x VLx25x0.56
x VLx25x0.56
VL =412.39V
Vph= VL/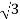 = 412.39/
= 412.39/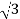 =238.09V
=238.09V
KVAR= = 14.96
= 14.96
Zph=238.09/25=9.52ohm
Rph=Zph Cos Ø= 9.52x0.56=5.33ohm
Xph=Zph Sin Ø = 9.52x0.83=7.88ohm
Q18) A balanced delta connected load consisting of three coils draws 8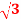 A at 0.5 p.f from 100V 3-phase ac supply. If the coils are reconnected in star across the same supply. Find the line current and total power consumed?
A at 0.5 p.f from 100V 3-phase ac supply. If the coils are reconnected in star across the same supply. Find the line current and total power consumed?
Sol: For Delta connection:
IL=8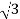 A
A
Iph= IL/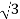 = 8A
= 8A
Vph=100V
Zph=100/8=12.5ohm
Rph=Zph Cos Ø=12.5x0.5 = 6.25ohm
Xph=Zph Sin Ø = 12.5x0.866=10.825ohm
P=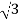 VLIL Cos Ø
VLIL Cos Ø
= 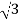 x 100x 8
x 100x 8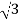 x0.5=1200W
x0.5=1200W
For Star Connection:
Vph= VL/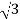 = 100/
= 100/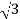 V=57.73V
V=57.73V
Zph=100/8=12.5ohm
Iph=57.73/12.5=4.62A
P=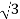 VLIL Cos Ø
VLIL Cos Ø
= x 100x 4.62x0.5
x 100x 4.62x0.5
P= 400W