UNIT-III
WAVES IN ONE DIMENSION
QUESTION BANK
1 Question: Write a note on standing sound waves?
Solution:
When a sound wave hits a wall, it is partially absorbed and partially reflected. A person far enough from the wall will hear the sound twice. This is an echo. In a small room the sound is also heard more than once, but the time differences are so small that the sound just seems to loom. This is known as reverberation.
Music is the sound that is produced by instruments or voices. To play most musical instruments you have to create standing waves on a string or in a tube or pipe. The perceived pitch of the sound is related to the frequency of the wave. The higher the frequency, the higher is the pitch.
Wind instruments produce sounds by means of vibrating air columns. To play a wind instrument you push the air in a tube with your mouth or a reed. The air in the tube starts to vibrate with the same frequency as your lips or the reed. Resonance increases the amplitude of the vibrations, which can form standing waves in the tube. The length of the air column determines the resonant frequencies. The mouth or the reed produces a mixture if different frequencies, but the resonating air column amplifies only the natural frequencies. The shorter the tube the higher is the pitch. Many instruments have holes, whose opening and closing controls the effective pitch.
In understanding standing waves, the most important aspect is boundary conditions. For sound wave in a tube different physics work at open and closed end of the tube. One may think that at open end the wave just propagates into the outside, but this is not so. Even at the open end the sound wave is reflected and standing wave is formed.
We can create a standing wave in a tube in different ways. It can be created in a tube which is open on both ends, and in a tube, which is open on one end and closed on the other end.
Open and closed ends reflect waves differently. The closed end of a tube is an antinode in the pressure or a node in the longitudinal displacement.
The open end of a tube is approximately a node in the pressure or an antinode in the longitudinal displacement.
Tubes with two open ends
The longest standing wave in a tube of length L with two open ends has displacement antinodes (pressure nodes) at both ends.
It is called the fundamental or first harmonic.
The next longest standing wave in a tube of length L with two open ends is the second harmonic.
It also has displacement antinodes at each end.
An integer number of half wavelength have to fit into the tube of length L.
L = nλ/2,
λ = 2L/n,
f = v/λ = nv/(2L).
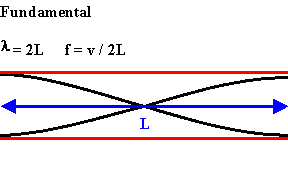 | 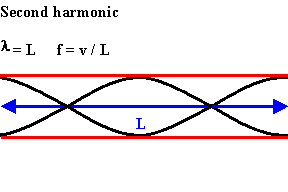 |
Figure 11 (a) | Figure 11 (b) |
Figure 11: Wave in tube with open end | |
For a tube with two open ends all frequencies fn = nv/(2L) = nf1, with n equal to an integer, are natural frequencies.
Tubes with one open and one closed end
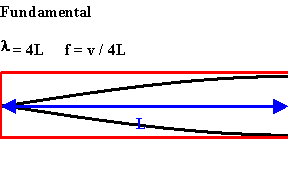 | 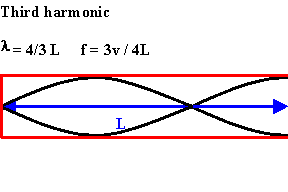 |
Figure 12 (a) | Figure 12 (b) |
Figure 12: Wave in tube with one open and one closed end | |
The longest standing wave in a tube of length L with one open end and one closed end has a displacement antinode at the open end and a displacement node at the closed end. This is the fundamental.
The next longest standing wave in a tube of length L with one open end and one closed end is the third harmonic.
An odd-integer number of quarter wavelength have to fit into the tube of length L.
L = nλ/4,
λ = 4L/n,
f = v/λ = nv/(4L), n = odd.
For a tube with one open end and one closed end all frequencies fn = nv/(4L) = nf1, with n equal to an odd integer are natural frequencies, i.e. only odd harmonics of the fundamental are natural frequencies.
2 Question: Derive wave equation in case of string?
Solution:
The type of wave that occurs in a string is called a transverse wave. In a transverse wave, the wave direction is perpendicular the direction that the string oscillates in.
Consider a uniform string stretched with a tension T and lying along the x-axis in the equilibrium position. The string is divided into a large number of infinitesimally small elements each of length A '. Each element is characterized by its x-coordinate. Figure 1 shows one such element of the string. We shall now obtain the equation of motion of such an element. In the equilibrium state, the forces acting on element AB are equal and opposite.
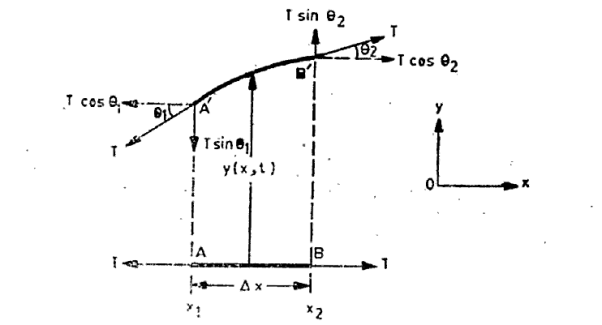
Figure 1: AB is an infinitesimal small element of string in the equilibrium position along x-axis. A’B’ is displaced position of the element.
The element is displaced along the y-axis to a new position A'B'. The element is no longer exactly straight; it has a slight curvature and the tension is tangential to the curve at A' and B'. If the displacement is small, the tension remains unchanged when the string is deformed.
Let y(x, t) be the transverse displacement of the element located at x at time t. When the string is released, the displacement of the element will change with time. Thus the displacement is a function of two variables x and t.
For an extremely small element (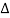 x
x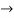 0) the net forces on the element along x and y directions are
0) the net forces on the element along x and y directions are
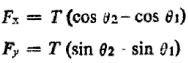
Where θ1 and θ2 are the directions of tangents to the string at the ends of the element, i.e. at x =x1 and x = x2 with x2—x1= 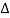 x.
x.
We are assuming that the transverse displacement is very small, so that θ1 and θ2 are small angles. We may, therefore, make the following approximations

The transverse component of tension on the element is, therefore, given by
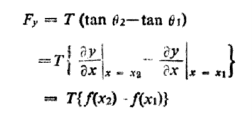 …………… (1)
…………… (1)
Where the function f(x) stands for 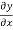 , Using Taylor’s series we have
, Using Taylor’s series we have
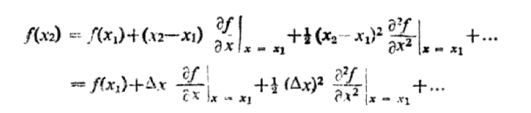
…………… (2)
We assume  x is small so
x is small so  x)2 and higher order can be ignored. Thus we may write
x)2 and higher order can be ignored. Thus we may write
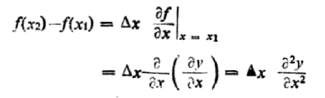 …………… (3)
…………… (3)
Where we have dropped the subscript x1 because, having ignored the higher order derivatives in Equation (2), it does not matter now where in the interval 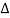 x we evaluate the x-derivative.
x we evaluate the x-derivative.
Notice that the space derivative is written as a partial derivative because now the displacement y(x, t) is a function of two variables x and t. In a complete form we would write Equation (3) as
f(x2) — f(x1) = 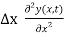 …………… (4)
…………… (4)
And Equation (1) as
Fy = 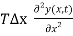 …………… (5)
…………… (5)
The equation of motion of the element is obtained from Newton's second law, namely, force = mass x acceleration.
Let μ be the linear density (mass per unit length) of the string. Therefore, the mass of the element of length 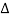 x = μ
x = μ  x
x
The acceleration of the element is 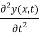
Hence Newton's force
μ 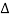 x
x 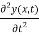
For dynamic equilibrium this force must balance the force fy given by equation (4). This gives the equation of motion of an element of the string, namely,
μ 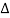 x
x 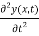 = T
= T 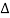 x
x 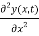 …………… (6)
…………… (6)
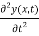 =
=
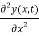 …………… (7)
…………… (7)
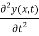 =
= 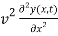 …………… (8)
…………… (8)
Where 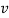 =
= 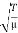 has dimensions of velocity so this is velocity of the wave.
has dimensions of velocity so this is velocity of the wave.
Equation (8) is a very famous second-order linear partial differential equation. It is called the classical wave equation.
We shall encounter this equation in many physical situations. The positive constant  (having dimensions of square of a velocity) is special to the string. In other physical situations, some other positive constant appears in its place in the wave equation. So far we have not explicitly stated which velocity the constant
(having dimensions of square of a velocity) is special to the string. In other physical situations, some other positive constant appears in its place in the wave equation. So far we have not explicitly stated which velocity the constant 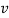 =
= 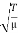 represents.
represents.
Every point on the string is moving with a time dependence of the form cosωt but that the amplitude of this motion is a function of the distance x of that point from the end of the string. Our assumed time dependence would require every point on the string to be instantaneously stationary at t = 0. If this is not so an initial phase angle must be introduced.
Thus we assume
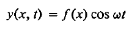 …………… (9)
…………… (9)
This then gives us
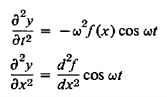 …………… (10)
…………… (10)
Since f(x) by definition is a function of x only, we can write 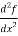 , instead of a partial derivative.
, instead of a partial derivative.
Substituting these derivatives in Equation (8) then gives us
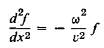 …………… (11)
…………… (11)
But this is the familiar differential equation satisfied by a sine or cosine function. Remembering that we have defined x = 0 as corresponding to one of the fixed ends of the string, with zero transverse displacement at all times, we know that an acceptable solution must be of the form
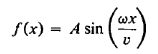 …………… (12)
…………… (12)
But we have the further boundary condition that the displacement is always zero at x = L. Hence we must also have
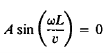 …………… (13)
…………… (13)
Hence
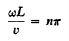 …………… (14)
…………… (14)
Where n is any (positive) integer. It will be convenient to introduce the number of cycles per unit time, v, equal to ω/2π. The frequencies of the permitted stationary vibrations are thus given by
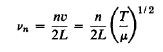 …………… (15)
…………… (15)
Where n, according to this calculation, may be 1, 2, 3, ... To infinity.
A vivid way of describing the shape of the string at any instant, in any particular mode n, is obtained by recognizing that the total length of the string must exactly accommodate an integral number of half-sine curves, as implied by Equation (14) We can therefore define a wavelength, associated with the mode n, such that
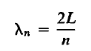 …………… (16)
…………… (16)
Then we can put
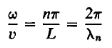 …………… (17)
…………… (17)
Hence, from Equation (12), the shape of the string in mode n is characterized by the following equation
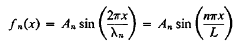 …………… (18)
…………… (18)
And the complete description of the motion of the string is thus as follows:
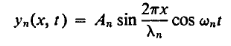 …………… (19)
…………… (19)
Where
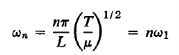 …………… (20)
…………… (20)
Since all the possible frequencies of a given stretched string are, according to the above analysis, simply integral multiples of the lowest possible frequency, ω1 a particular interest attaches to this basic mode—the fundamental.
It is the frequency of the fundamental that defines what we recognize as the characteristic pitch of a vibrating string, and which therefore defines for us the tension required to obtain a certain note from a string of given mass and length.
3 Question: Write a note Harmonic waves?
Solution:
The simplest normal mode, where the string vibrates in one loop, is labelled n = 1 and is called the fundamental mode or the first harmonic. The second mode (n = 2), where the string vibrates in two loops, is called the second harmonic. The nth harmonic consists of n vibrating loops. The set of all normal modes {n = 1, 2, 3, 4, 5, ... } is the harmonic spectrum. The spectrum of natural frequencies is { ω1, ω 2, ω3, ω4, ω5, ... }. Note that the frequency ω n of mode n is simply a whole-number multiple of the fundamental frequency: ω n = nω1.
The mode with three loops vibrates three times as fast as the mode with one loop. Harmonics are the basis of harmony in music. The sectional vibrations of a string as one whole, two halves, three thirds, and so on, are very special because these vibrations produce musical tones that sound the “most pleasant” when sounded together, i.e. they represent the most harmonious combination of sounds. This explains the origin of the word “harmonic”.
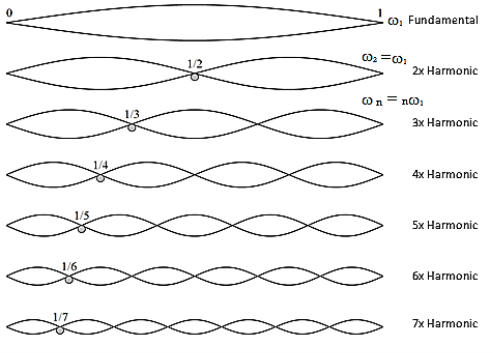
Figure 2: Harmonic waves
In a stringed instrument such as a piano, the string is struck once at some chosen point. At the moment of impact, and for a brief instant thereafter, the string is sharply pushed aside near this point, and its shape is nothing like a sine curve. Shortly thereafter, however, it settles down to a motion which is a simple super-position of the fundamental and a few of its lowest harmonics. It is a physically very important fact that these vibrations can occur simultaneously and to all intents independently of one another. Their mutual independence can be demonstrated by suddenly stopping the transverse motion of the string at a point that is a node for some harmonics but not for others.
Those component vibrations for which the point is a node will continue unaffected; the others will be quenched.
Thus, for example, if a piano string has been set sounding loudly by striking the key, which is kept held down, and the string is then touched one third the way along its length, all component vibrations are stopped except the third, sixth, etc., multiples of the fundamental frequency.
These Figures reveal that there are certain points on the string which are permanently at rest; the number of these points depends upon the number of the mode under study. These points are called nodes.
The points where the displacement is maximum are called antinodes.
It states that the frequencies of all the overtone of such a string are integral multiples of the fundamental frequency.
Overtones bearing this simple relation to the fundamental are called harmonics. The fundamental being first harmonic and it is called first overtone (twice the fundamental frequency ) being the second harmonic and so on.
4 Question: Derive reflection and transmission coefficients for a wave travels at a boundary?
Solution:
Let us suppose two waves string 1 and 2 of different linear densities are joined together to form a composite system. Let us suppose that both string have same tension T. The linear densities of the strings 1 and 2 are 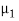 and
and 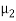 .
.
The wave velocities in strings 1 and 2 are given as
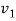 =
= 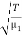 and
and 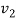 =
= 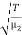
Let us suppose a wave (called the incident wave) is travelling in the +x direction on string 1. The particle d displacements of string 1 are given by, yi(x,t) = Ai sin (ωt—k1x)
Where k1 = 2π/λ1 = 2πν /v1 and Ai is the amplitude of the incident wave.
When this wave reaches the boundary (which we shall take at x = 0) separating the two strings, it is partly reflected and partly transmitted at the boundary. The reflected wave travels on string 1 in the negative x direction and the transmitted wave travels on string 2 in the positive x direction as shown n figure.
The particle displacements due to these waves are, therefore given by
yr(x,t) = Ar sin (ωt+k1x) …………. (1)
yt(x,t) = At sin (ωt—k2x)…………. (2)
Where k2 = 2π/λ2 = 2πν /v2 and Ar and At are the amplitudes of the reflected and transmitted waves respectively.
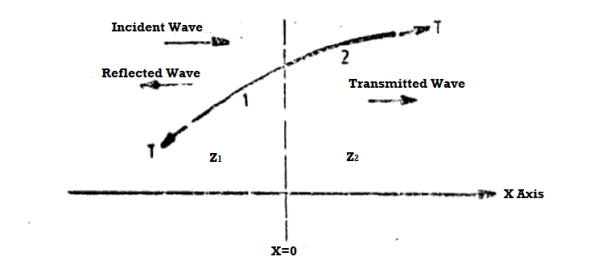
Figure 3: Reflection and transmission of waves at a boundary
Boundary conditions
The point x = 0 at the boundary undergoes oscillations under the combined influence of the incident and reflected waves in string 1. It then acts as a source of transmitted waves travelling in string 2. The boundary conditions to be satisfied at x = 0 are
(1) The displacement is the same immediately to the left and to the right of the boundary at x = 0, i.e. y(x, 0) is continuous across boundary at x = 0. Therefore, velocity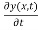 is also continuous.
is also continuous.
(2) The restoring force or transverse component of Tension [-T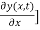 is continuous across the boundary at x = 0. To understand this, let us imagine that there is an infinitesimal element of mass at x = 0. If the gradient
is continuous across the boundary at x = 0. To understand this, let us imagine that there is an infinitesimal element of mass at x = 0. If the gradient 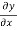 is not continuous, this would give rise to a net transverse force acting on this infinitesimally small mass of the string at x = 0. Consequently this element will have an infinite acceleration which is not permitted.
is not continuous, this would give rise to a net transverse force acting on this infinitesimally small mass of the string at x = 0. Consequently this element will have an infinite acceleration which is not permitted.
Recalling that y(x,t) in string 1 is due to a superposition of the displacement due to the incident and reflected waves and y(x,t) in string 2 is due only to the transmitted wave and using the boundary condition (1) we have
yi(x,t) + yr(x,t) = yt(x,t)…………. (3)
Ai sin (ωt—k1x) + Ar sin (ωt+k1x) = At sin (ωt—k2x) …………. (4)
Setting x=0 we have
Ai sin ωt + Ar sin ωt = At sin ωt
For all t, which gives
Ai + Ar = At …………. (5)
Boundary condition (2) requires that at x=0, we have
-T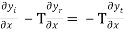 …………. (6)
…………. (6)
Or
Ai k1T cos (ωt—k1x) + Ar k1T cos (ωt+k1x) = At k2T cos (ωt—k2x)
Setting x=0 we have (for all t)
k1T (Ai - Ar) = k2T At…………. (7)
Now
k1T = 2πνT/v1 = 2πν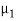
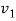 =2πν
=2πν 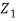 (
(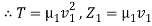 )
)
And
k2T = 2πν 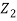
We then have
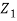 (Ai - Ar) =
(Ai - Ar) = 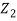 At
At
r12 = 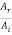 =
= 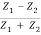 …………. (8)
…………. (8)
t12 = 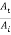 =
= 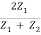 …………. (9)
…………. (9)
Where r12 and t12 are the reflection and transmission amplitude coefficients when a wave travels from string 1 to string 2. The ratio 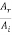 is the fraction of the incident amplitude reflected at the boundary and the ratio
is the fraction of the incident amplitude reflected at the boundary and the ratio 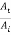 is the fraction of the incident amplitude transmitted across the boundary.
is the fraction of the incident amplitude transmitted across the boundary.
These fractions depend only on the impedances and are independent of the angular frequency ω of the incident wave. If the string is rigidly fixed at x = 0, say, by attaching this end to a wall, then the medium 2 is infinitely massive which means that 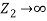 .
.
In this case 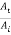 =0 giving
=0 giving 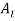 = 0 indicating that there is no transmitted wave and
= 0 indicating that there is no transmitted wave and 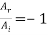 or
or 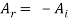 which means that the incident wave is completely reflected with a reversal in amplitude. The reversal of amplitude means a phase change of π on reflection.
which means that the incident wave is completely reflected with a reversal in amplitude. The reversal of amplitude means a phase change of π on reflection.
It is clear from equation (8) that if Z2 >Z1, the ratio 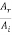 will be negative indicating a phase change of π on reflection. Thus we conclude that if a wave travelling in a medium of lower impedance meets the boundary of a medium of higher impedance (i.e. a medium in which the wave velocity is smaller), the wave reflected at the boundary undergoes a phase change of it.
will be negative indicating a phase change of π on reflection. Thus we conclude that if a wave travelling in a medium of lower impedance meets the boundary of a medium of higher impedance (i.e. a medium in which the wave velocity is smaller), the wave reflected at the boundary undergoes a phase change of it.
On the other hand if Z2< Z1 the ratio 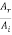 is positive. Thus, if a wave is reflected at the boundary of lower impedance (i.e. a medium in which the wave velocity is higher), the reflected wave does hot undergo any phase change.
is positive. Thus, if a wave is reflected at the boundary of lower impedance (i.e. a medium in which the wave velocity is higher), the reflected wave does hot undergo any phase change.
Furthermore, equation (9) shows that the ratio 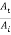 always remains positive independent of whether Z2 is less than or more than Z1. This shows that the transmitted wave does not undergo any phase change is illustrated in Figure 4 which shows reflection and transmission of a pulse at a boundary between two strings.
always remains positive independent of whether Z2 is less than or more than Z1. This shows that the transmitted wave does not undergo any phase change is illustrated in Figure 4 which shows reflection and transmission of a pulse at a boundary between two strings.
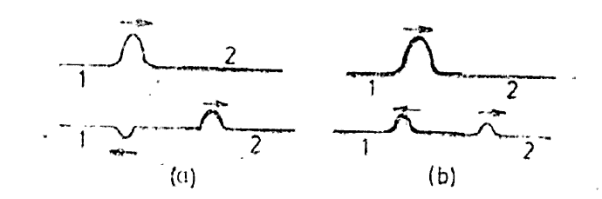
Figure 4: (a) Reflection and transmission of a pulse when string 2 has higher impedance. (b) Reflection and transmission of a pulse when string 2 has lower impedance.
If wave travels from string 2 to string 1 the r21 and t21 are the reflection and transmission amplitude coefficients
r21 = 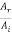 =
= 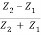 …………. (10)
…………. (10)
t21 = 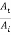 =
= 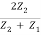 …………. (11)
…………. (11)
5 Question: Discuss the reflection and transmission coefficients of Energy at the Boundary?
Or
Prove that the rate at which energy arrives at the boundary with the incident wave is equal to the rate at which energy leaves the boundary with the reflected and transmitted waves.
Solution:
Reflection mid Transmission
Waves are a very useful mechanism for the transport of energy in a medium. It is interesting to consider what happens to the energy in a wave when it meets a boundary between two media of different impedances. As the wave travels along the string, each part of the string is thrown into harmonic oscillations with the passage of time.
We know that the rate at which energy is carried per unit length along the string is given by
P =  μvA2 ω2…………. (12)
μvA2 ω2…………. (12)
Let us now compute the rates at which energy is incident, reflected and transmitted at the boundary at x = 0. The rate of incident energy is the rate at which the energy is carried by the incident wave which is given by
Pi =  Z1Ai2 ω2…………. (13)
Z1Ai2 ω2…………. (13)
Similarly the rates of reflected and transmitted energies respectively are
Pr =  Z1Ar2 ω2…………. (14)
Z1Ar2 ω2…………. (14)
Pt =  Z2At2 ω2…………. (15)
Z2At2 ω2…………. (15)
Using Equations (8) and (9) we find that
Pr =  Z1(
Z1(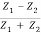 ) ω2 Ai2…………. (16)
) ω2 Ai2…………. (16)
Pt = 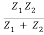 ω2 Ai2…………. (17)
ω2 Ai2…………. (17)
And
Pr + Pt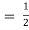 Z1ω2 Ai2 (
Z1ω2 Ai2 (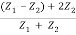 )=
)=  Z1ω2 Ai2 = Pi…………. (19)
Z1ω2 Ai2 = Pi…………. (19)
In other words, the rate at which energy arrives at the boundary with the incident wave is equal to the rate at which energy leaves the boundary with the reflected and transmitted waves. This is consistent with the conservation of energy at the junction of two media. Thus, energy is conserved. All the energy arriving at the boundary with the incident wave leaves the boundary with the reflected and transmitted waves. This is expected since we have assumed that there is no absorption of energy at the boundary. The reflection and transmission energy coefficients are given by
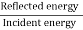 =
= 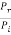 =
= 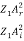 =
= 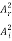 = (
= (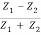 )2
)2
 =
= 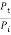 =
= 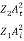 =
= 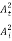 =
= 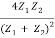
Reflection coefficient +Transmission coefficient = 1
Also if Z1 = Z2, no energy is reflected and the impedances are said to be matched.
6 Question: Discuss Impedance matching?
Or
Prove that the impedance of the coupling medium is the harmonic mean of the two impedances to be matched
Solution:
Impedance matching represents a very important practical problem in the transfer of energy. Long distance cables carrying energy must be accurately matched at all joints to avoid wastage from energy reflection. The power transfer from any generator is a maximum when the load matches the generator impedance. A loudspeaker is matched to the impedance of the power output of an amplifier by choosing the correct turns ratio on the coupling transformer. This last example, the insertion of a coupling element between two mismatched impedances, is of fundamental importance with applications in many branches of engineering physics and optics. We shall illustrate it using waves on a string, but the results will be valid for all wave systems.
We have seen that when a smooth joint exists between two strings of different impedances, energy will be reflected at the boundary. We are now going to see that the insertion of a particular length of another string between these two mismatched strings will allow us to eliminate energy reflection and match the impedances.
In Figure (5) we require to match the impedances Z1= ρ1c1 and Z3 = ρ3c3 by the smooth insertion of a string of length l and impedance Z2= ρ2c2. Our problem is to find the values of l and Z2.
The incident, reflected and transmitted displacements at the junctions x = 0 and x = l are shown in Figure 5 and we seek to make the ratio
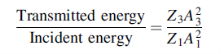
Equal to unity.
The boundary conditions are that y and T 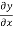 are continuous across the junctions x = 0 and x =l.
are continuous across the junctions x = 0 and x =l.
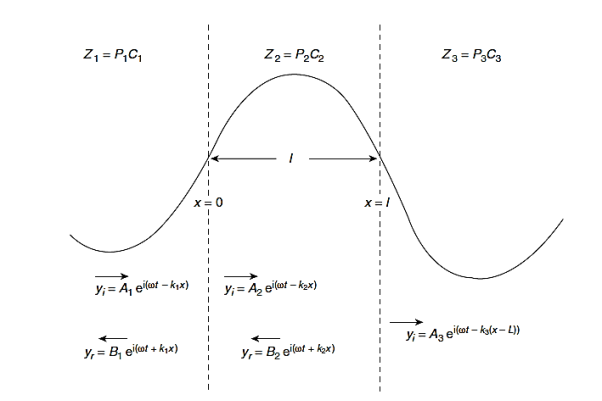
Figure 5: The impedances Z1 and Z3 of two strings are matched by the insertion of a length l of a string of impedance Z2. The incident and reflected waves are shown at boundary x=0 and x=l. The impedances are matched when 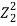 = Z1Z3 and for l= λ/4 in Z2, results which are true for waves in all media
= Z1Z3 and for l= λ/4 in Z2, results which are true for waves in all media
Between Z1 and Z2 the continuity of y gives
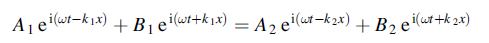
Or
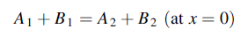 ……………(1)
……………(1)
Similarly the continuity of T 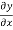 at x=0 gives
at x=0 gives
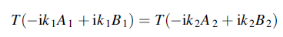
Dividing this equation by ω and remembering that
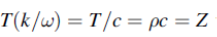
We have
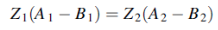 ……………(2)
……………(2)
Similarly at x= l, the continuity of y gives
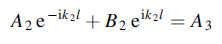 ……………(3)
……………(3)
And the continuity of T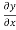 gives
gives
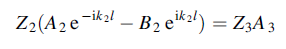 ……………(4)
……………(4)
From the four boundary equations (1), (2), (3) and (4) we require the ratio A3=A1.using above equations
We use equations (1) and (2) to eliminate B1 and obtain A1 in terms of A2 and B2. We then use equations (3) and (4) to obtain both A2 and B2 in terms of A3. Equations (1) and (2) give
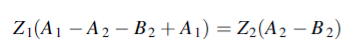
Or
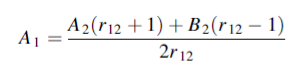 ……………(5)
……………(5)
Where
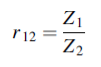
Equations (3) and (4) give
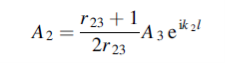 ……………(6)
……………(6)
And
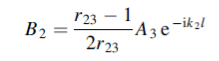
Where
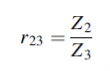
Where equation (5) and (6) gives
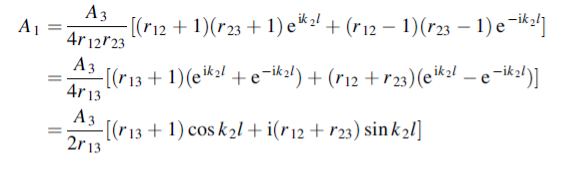
Where
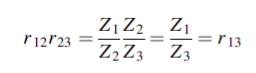
Hence
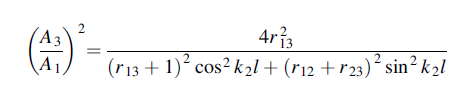
or
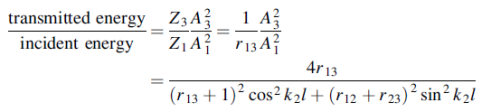
If we choose
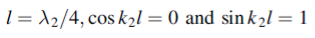
We have
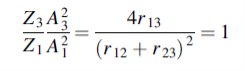
When r12 =r23
That is when
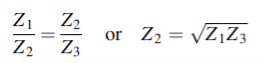
We see, therefore, that if the impedance of the coupling medium is the harmonic mean of the two impedances to be matched and the thickness of the coupling medium is
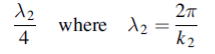
All the energy at frequency ω will be transmitted with zero reflection. The thickness of the dielectric coating of optical lenses which eliminates reflections as light passes from air into glass is one quarter of a wavelength. The ‘bloomed’ appearance arises because exact matching occurs at only one frequency. Transmission lines are matched to loads by inserting quarter wavelength stubs of lines with the appropriate impedance.
7 Question: Explain standing waves on a String of fixed length?
Solution:
Standing Waves on a String of Fixed Length
Consider a string of length L stretched with a tension T along the x-axis with its ends at A (x= 0) and B(x = L) rigidly fixed (Figure 6). A transverse wave is produced by creating a harmonic disturbance near the end A. The wave travels along the string in the +x direction and gets reflected at end B which travels in –x direction. The interference between two oppositely travelling wave ends gives rise to standing wave on the string. Let us consider the simplest case of a monochromatic incident wave of a single frequency co and amplitude Ai. The displacement at time t of a particle, say C, 1ocated at x due to the incident wave travelling in the +x direction is given by
yi(x,t) = Ai sin (ωt—kx) = Ai sin {k(vt—x)}…………..(1)
Where k = 2π/λ, λ is the wavelength of the wave, v =ω/k is velocity of the wave
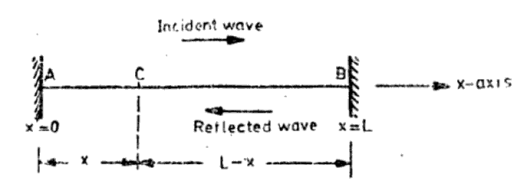
Figure 6: Standing waves on a string fixed at both ends x = 0 and x = L
Let us find out the displacement at time t of the same particle C located at x due to the wave reflected from the fixed end B.
The reflected wave can be written as
yr(x,t) = Ar sin {k(vt—x’)}…………..(2)
Where Ar, is the amplitude of the reflected wave and x’ must be the distance travelled by the wave of equation (1) from A to R and then to C, i e. x’ = x-(L-x)= 2L-x.
Hence the displacement at time t of particle C at x due to the reflected wave must be given by
yr(x,t) = Ar sin {k(vt+x-2L)}
The sine function involves (vt+x) which represents a wave in the - x direction, the direction of propagation of the wave reflected at B.
From the principle of superposition, the resultant displacement at time t at any point x is given by
y(x,t) = yi(x,t) + yr(x,t)
= Ai sin {k(vt—x)} + Ar sin {k(vt+x-2L)}…………..(3)
Since the ends x 0 and x = L are rigidly fixed, boundary conditions are (i) y = 0 at x = 0 and (ii) y = 0 at x =L. Using condition (II) in Eq. (8.7) gives
0 = Ai +sin {k(vt—L)} + Ar sin {k(vt-L)}
0=(Ai + Ar) sin {k(vt—L)}…………..(4)
Which is satisfied for all t values
Ai + Ar =0
Ar = - Ai =-A
The reversal of the amplitude of the reflected wave implies a phase change 1800 on reflection at the rigid end x = L. Putting Ar = - Ai =-A in equation (3) we have
y(x,t) = A {sin k(vt—x) - sin k(vt+x-2L)}
We know that  = 2
= 2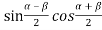 using this identity, we get
using this identity, we get
y(x,t) = 2A {sin k(L—x) cosk(vt -2L)}…………..(5)
At x=L equation (5) gives y=0, which is true since end is rigid so there is no resultant motion.
The first boundary conditions, namely y=0 also at x=0 remains to be satisfied.
Put x=0 in equation
(5) require y to be zero at all values of t.
SinkL =0
KL =0,π, 2π, 3π……..
knL = 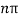
kn = 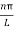 where n is an integer 0,1,2,3,…..…………..(6)
where n is an integer 0,1,2,3,…..…………..(6)
The allowed frequencies are ω =kv
ωn =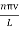 …………..(7)
…………..(7)
νn =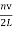 =
= 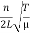 …………..(8)
…………..(8)
Using equation (5) and (6) we get
y(x,t) = 2A {sin 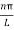 (L—x) cos
(L—x) cos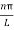 (vt -L)}
(vt -L)}
y(x,t) = -2A (sin 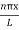 cos
cos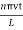 )…………..(9)
)…………..(9)
Equation (9) can be written as
y(x,t) = -2A (sinknx cosωnt )…………..(10)
Equation (9) is the equation of a standing or stationary wave. It is obvious that this equation does not represent a travelling wave since it no longer has the characteristic form involving (ωt–kx) or (ωt+kx) in the argument of the trigonometric function.
Modes of Vibration
Notice that the frequencies given by equation (8) are just the frequencies of the normal modes of a string fixed at both ends.
The mode with n = 0 is unphysical since then ν = 0 implying that there is no vibration at all. The mode with n = 1 is called the fundamental mode. The frequency and particle displacements in this mode are given by
ν1 = 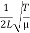
y(x,t) = -2A (sin 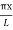 cos
cos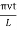 )
)
Notice that the points x = 0 and x = L are permanently at rest. These points on the string are called nodal points or nodes. But the point x = 1/2 has a maximum displacement. These points are called antinodes. Figure (7) shows the particle displacement in the fundamental mode.
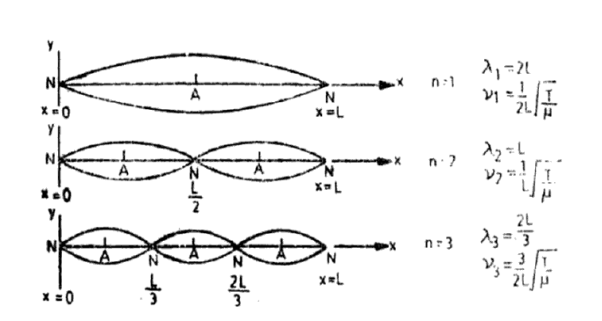
Figure 7: Standing Waves on a string of length L fixed at both ends Modes of string: first three harmonics n = 1, 2 and 3.
The mode with n= 2 is called the second harmonic. The frequency and particle displacements in this mode are given by
ν2 = 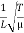 = 2 ν1
= 2 ν1
y(x,t) = -2A (sin 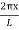 cos
cos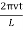 )
)
Notice that, in addition to nodes at x=0 and x=L, there is another node at x= L/2. The antinodes are at, L/4, 3L/4. This mode is shown in Figure 7(b). Figure 7(c) shows the third harmonic.
We find that in the nth harmonic there are (n—1) positions (between the fixed ends) equally spaced along the string where the displacement is always zero. These points marked N are the nodes in a standing wave pattern.
8 Question: Derive wave equations for longitudinal vibrations of a rod?
Solution:
Longitudinal vibrations of a rod
Consider a cylindrical metal rod of uniform cross-sectional area. When the rod is struck lengthwise (or stroked) it begins to vibrate. The vibrations are in the audible range of frequencies. Let us obtain the equation of motion of the particles of the rod.
Suppose the rod is lying along the x-axis. We divide the rod into a large number of small slices each of length, say,  x.
x.
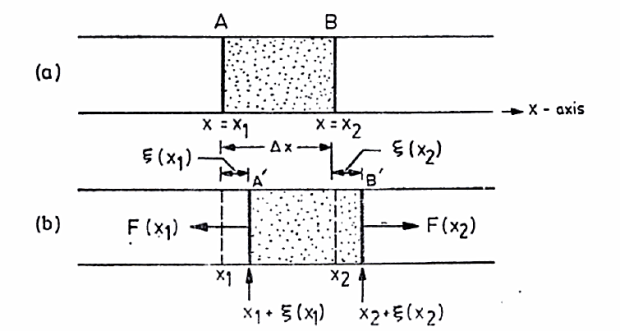
Figure 8: Longitudinal vibrations of a rod (a) Equilibrium State (b) Disturbed State
Consider one such slice or element AB as shown in Figure. The particles at the end A are at a distance of x1 = x from some origin and those at end B are at a distance x2 = x+ x.
x.
When the rod is struck lengthwise the particles of the rod are displaced along the x-axis, i.e. along the length of the rod. In other words, the particle displacements are longitudinal rather than transverse as in the case of a string.
We shall use the symbol ξ to denote the displacement, along the x-axis, of the particles in a plane at x = xi perpendicular to the axis of the rod. We shall now obtain the equation of motion of a thin slice AB of the rod which, in the undisturbed state, is contained between x and x+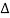 x as shown in Figure 8(a).
x as shown in Figure 8(a).
Figure 8(b) shows the displaced position of the slice. Let the x-coordinate of the end A of the slice in the displaced position be x1 +ξ (x1) so that ξ (x1) represents the displacement of the particles at the plane x1. Similarly let x2 +ξ (x2) be the x-coordinate the particles originally located at a plane x = x2 so that ξ (x2) is the displacement of the particles at the plane x2.
Therefore, Change in length of the slice
= ξ (x2) - ξ (x1)
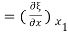
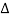 x
x
Where we have used Taylor's expansion
ξ (x2) = ξ (x1) + 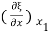
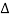 x +………
x +………
And retained terms up to order (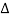 x) as in the case of a string. Since the original length of the slice is
x) as in the case of a string. Since the original length of the slice is 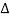 x. The longitudinal strain Ɛ at x1 is given by
x. The longitudinal strain Ɛ at x1 is given by
ξ (x1) = 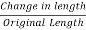 =
= 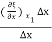 =
= 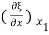
If Y is the young’s modulus of the material of the rod, the stress S at x1 is given by
S(x1) = Y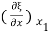
Similarly the stress at x2 is given by
S(x2) = Y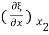
The net stress on the element AB is
S(x2) - S(x1) = Y [f(x2)-f(x1)]
Where f(x) =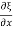 Since f(x2) - f(x1) =
Since f(x2) - f(x1) = 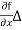 x, we have
x, we have
S(x2) - S(x1) = Y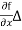 x, we have
x, we have
= Y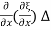 x
x
= Y 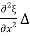 x
x
If 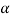 is a cross sectional area of the rod, net longitudinal force on the element is given by
is a cross sectional area of the rod, net longitudinal force on the element is given by
F(x)= F(x2) - F(x1) =Stress x Area = Y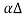 x
x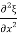
To obtain the equation of motion, we apply Newton's law to the slice. If ρ is the density of the rod, the mass of the slice is ρ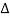 x. Therefore, Newton's force F' is mass x acceleration, i.e.
x. Therefore, Newton's force F' is mass x acceleration, i.e.
F’ = ρ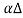 x
x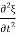
In dynamic equilibrium, the two force F and F’ must balance, giving
ρ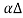 x
x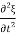 = Y
= Y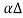 x
x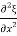
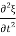 =
= 
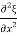
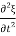 =
= 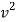
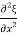
With 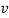 =
= 
Notice that 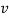 has the dimensions of a velocity will be identified as the velocity of longitudinal (is sound) waves travelling in the rod
has the dimensions of a velocity will be identified as the velocity of longitudinal (is sound) waves travelling in the rod
As the wave travels along the rod, different particles acquire a displacement ξ (x, t) which is a function of both x and t. It may be remarked that the picture presented above is a crude one because the particles of the rod are bouncing back and forth due to thermal agitation, even when there is no sound. The quantity ξ (x, t) actually measures the average displacement, due to sound wave, of those particles whose average position was originally at x.
9 Question: Explain sound wave? Derive formula for speed of wave?
Solution:
Longitudinal waves propagate as sound waves in all phases of matter, plasmas, gases, liquids and solids, but we shall concentrate on gases and solids. In the case of gases, limitations of thermodynamic interest are imposed; in solids the propagation will depend on the dimensions of the medium. Neither a gas nor a liquid can sustain the transverse shear necessary for transverse waves, but a solid can maintain both longitudinal and transverse oscillations.
The wave we analyse here is sound in an elastic medium, such as air. Let’s consider a one dimensional wave travelling in the x direction. We’ll consider a section with cross section A. Let us suppose a wave travelling through a pipe, and neglect the viscous and thermal interactions at the wall. We’ll consider some point here to analyse sound propagation:
- First, look at how spatial variations in displacement produce compression or expansion and thus derive how the pressure depends on displacement.
- Second, we’ll apply Newton’s second law to see how spatial variations in pressure accelerate the air, and thus change the displacement.
First we will analyse how displacement affects pressure
Let us consider the motion of an element of our medium, whose position, when there is no sound wave disturbance, is between x1 and x2. We’ll make the distance between x1 and x2 much less than a wavelength of sound.
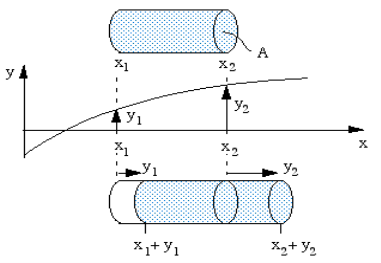
Figure 9: Wave travelling through a pipe
So the undisturbed volume of this element is
V = A(x2 – x1)
And, using the density ρ and cross section A, its mass is
m = ρV = ρA(x2 − x1) ………… (1)
Let y is the average displacement of the molecules in the x direction at any time
y is written as average displacement because in gas, the individual molecules have their own random motion superimposed on the average or bulk motion that we are going to observe.
At some time t, medium show displacement. It is displaced from its equilibrium position such that the medium whose equilibrium position is at x1 is moved to x1 + y1 and the medium whose equilibrium position is at x2 is moved to x2 + y2.
The new volume of our element of air is
V + δV = A(x2 + y2 − x1 − y1) and, using (1), we have
δV = A(y2 − y1).
When a medium is compressed, its pressure rises. The ratio between the pressure increase p and the proportional volume reduction is called the volumetric modulus of elasticity 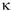 , defined by
, defined by
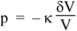
So the pressure in our element, when it is displaced as shown in above diagram, is
 , so
, so 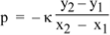
In the limit where x2 – x1 is very small, this gives us the relation between displacement y and pressure p:
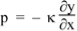 …………(2)
…………(2)
Now to apply Newton’s second law. The absolute pressure at x1 is PAtm + p1, where PAtm is undisturbed atmospheric pressure. So the pressure on the left, acting on area A, exerts a force to the right of (PAtm + p1)A. Similarly, at x2, the force on the right, acting to the left, is (PAtm + p2)A. So the net force to the right is
F = (p1 − p2)A.
Let’s take the average displacement of our element as y (where y1 < y < y2). So, taking the second derivative with respect to time, its acceleration to the right is
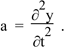
Equation (1) gives the mass and the two equations above give F and a, so F = ma becomes
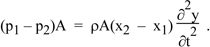
We rearrange, reverse the order of p1 and p2 and cancel A to give
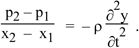
In the limit of very small distance x2 – x1, this gives
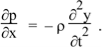
This is the wave equation.
Equation (2) gave us 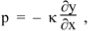 so combining this with the equation above we have
so combining this with the equation above we have
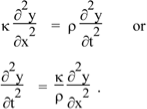 (3)
(3)
One dimensional wave equation. In case of a string with tension T and linear density μ, we had
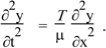
We showed then that this has wave solution with speed 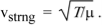
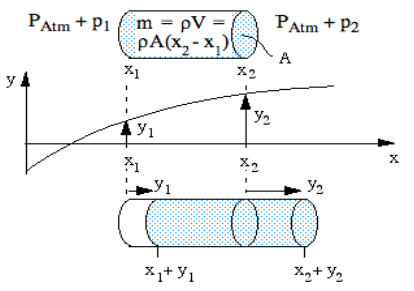
Figure 10: Wave travelling through a pipe under pressure
The solution is given by
y = ym sin (kx − ωt)
And take derivatives, we have
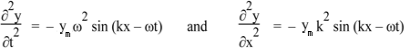
From the above solution it is given that (ω/k)2 = 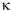 /ρ. Now ω/k is the wave speed so we have, for the speed of sound:
/ρ. Now ω/k is the wave speed so we have, for the speed of sound:
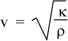
The tension in the string provides a restoring force; so does the elasticity of the medium here. The inertia was provided by the mass per unit length μ of the string, here by the mass per unit volume ρ of the medium.
Although we imagined that our element was air, we have so far only assumed that it is elastic. So this equation is true for longitudinal waves in any elastic medium. For air, we can give a value for the elastic modulus 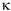 .
.
Let us discuss the case of ideal gas. We show that, during adiabatic expansion and compression, the pressure P and volume V are related
PVγ = constant
Where γ is the adiabatic constant, or the ratio of the specific heat at constant pressure to the specific heat at constant volume, which is about 1.4 for air. Taking natural logs of both side, we have
Ln P + γ ln V = constant.
Taking derivatives gives us
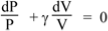
So 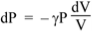
The definition of the bulk modulus, expressed as a differential, is
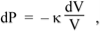
So combining the two equations above we have
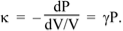
So the speed of sound in an ideal gas is
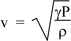
For air at atmospheric pressure (P = 101 kPa) and at T = 20 °C, the density is 1.20 kg.m−3. Taking γ = 1.4 gives a speed of sound of 343 m.s−1.
Specific acoustic impedance
Let’s relate the velocity and pressure, using the solution above:
y = ym sin(kx − ωt)
The particle velocity is
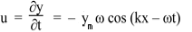
Using equation (2), we have
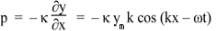
The specific acoustic impedance z of a medium is defined by p/u, so, using the equations above
z = κk/ω.
Above, we had κ/ρ = v2, above so κ = ρv2. We also had ω/k = v. Substituting these gives the specific acoustic impedance
z = ρv.
10 Question: A string of length l = 0.5 m and mass per unit length 0.01 kgm-1 has a fundamental frequency of 250 Hz. What is the tension in the string?
Solution:
We have
ν =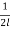
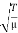
Or T = 4l2 ν2 μ = 4 × (0.5)2 × (250)2 × 0.01
= 625 N.
11 Question: A steel wire is stretched between two clamps 100 cm apart with a tension winch produces an extension of 0.608 cm in it. Calculate the fundamental frequency of its transverse vibration Density of steel = 7600 kgm-3, and its Young's modulus = 2x1011 Nm-2. Winch overtone of the string will correspond to a frequency of 800 Hz?
Solution:
Let L be the length of the wire and 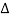 L the extension produced when it is stretched with a tension T. Then Y, the Young's modulus of the wire is given by
L the extension produced when it is stretched with a tension T. Then Y, the Young's modulus of the wire is given by
Y = 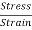 =
= 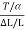 =
= 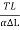
Where 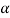 it the cross-sectional area of the wire. Thus
it the cross-sectional area of the wire. Thus
T = 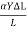 ………….(1)
………….(1)
Now the fundamental frequency of the wire is given by
ν1 = 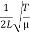 ………….(2)
………….(2)
But 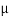 =mass per unit length, =
=mass per unit length, =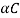 where
where 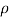 is the density of the wire.
is the density of the wire.
Using this 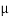 and Eq. (1) in Eq. (2), we get
and Eq. (1) in Eq. (2), we get
ν1 = 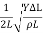
Putting the numerical values (In SI units), we have
ν1 = 200 Hz
Evidently the fourth harmonic (or the third overtone) has a frequency of 800 Hz.
12 Question: Two wires of radii r and 2r respectively are welded together end to end. This combination is used as a sonometer wire kept under tension T. The welded point is midway between the two bridges. What would be the ratio of the number of loops formed in the wires such that the joint is a node when stationary vibrations are set up in the wires?
Solution
Let n1 and n2 be the number of loops formed in the wires of radii r and 2r respectively.
Then
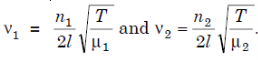
Since the welded wire is continuous, ν1 = ν2 and
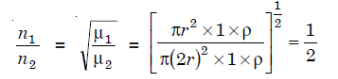
Where ρ = density of the material of the wires.
UNIT-III
WAVES IN ONE DIMENSION
QUESTION BANK
1 Question: Write a note on standing sound waves?
Solution:
When a sound wave hits a wall, it is partially absorbed and partially reflected. A person far enough from the wall will hear the sound twice. This is an echo. In a small room the sound is also heard more than once, but the time differences are so small that the sound just seems to loom. This is known as reverberation.
Music is the sound that is produced by instruments or voices. To play most musical instruments you have to create standing waves on a string or in a tube or pipe. The perceived pitch of the sound is related to the frequency of the wave. The higher the frequency, the higher is the pitch.
Wind instruments produce sounds by means of vibrating air columns. To play a wind instrument you push the air in a tube with your mouth or a reed. The air in the tube starts to vibrate with the same frequency as your lips or the reed. Resonance increases the amplitude of the vibrations, which can form standing waves in the tube. The length of the air column determines the resonant frequencies. The mouth or the reed produces a mixture if different frequencies, but the resonating air column amplifies only the natural frequencies. The shorter the tube the higher is the pitch. Many instruments have holes, whose opening and closing controls the effective pitch.
In understanding standing waves, the most important aspect is boundary conditions. For sound wave in a tube different physics work at open and closed end of the tube. One may think that at open end the wave just propagates into the outside, but this is not so. Even at the open end the sound wave is reflected and standing wave is formed.
We can create a standing wave in a tube in different ways. It can be created in a tube which is open on both ends, and in a tube, which is open on one end and closed on the other end.
Open and closed ends reflect waves differently. The closed end of a tube is an antinode in the pressure or a node in the longitudinal displacement.
The open end of a tube is approximately a node in the pressure or an antinode in the longitudinal displacement.
Tubes with two open ends
The longest standing wave in a tube of length L with two open ends has displacement antinodes (pressure nodes) at both ends.
It is called the fundamental or first harmonic.
The next longest standing wave in a tube of length L with two open ends is the second harmonic.
It also has displacement antinodes at each end.
An integer number of half wavelength have to fit into the tube of length L.
L = nλ/2,
λ = 2L/n,
f = v/λ = nv/(2L).
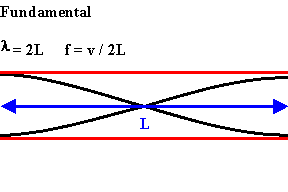 | 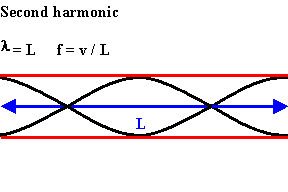 |
Figure 11 (a) | Figure 11 (b) |
Figure 11: Wave in tube with open end | |
For a tube with two open ends all frequencies fn = nv/(2L) = nf1, with n equal to an integer, are natural frequencies.
Tubes with one open and one closed end
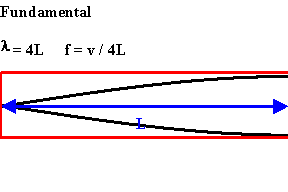 | 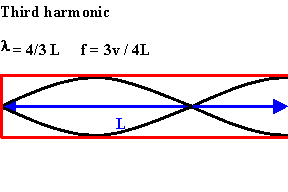 |
Figure 12 (a) | Figure 12 (b) |
Figure 12: Wave in tube with one open and one closed end | |
The longest standing wave in a tube of length L with one open end and one closed end has a displacement antinode at the open end and a displacement node at the closed end. This is the fundamental.
The next longest standing wave in a tube of length L with one open end and one closed end is the third harmonic.
An odd-integer number of quarter wavelength have to fit into the tube of length L.
L = nλ/4,
λ = 4L/n,
f = v/λ = nv/(4L), n = odd.
For a tube with one open end and one closed end all frequencies fn = nv/(4L) = nf1, with n equal to an odd integer are natural frequencies, i.e. only odd harmonics of the fundamental are natural frequencies.
2 Question: Derive wave equation in case of string?
Solution:
The type of wave that occurs in a string is called a transverse wave. In a transverse wave, the wave direction is perpendicular the direction that the string oscillates in.
Consider a uniform string stretched with a tension T and lying along the x-axis in the equilibrium position. The string is divided into a large number of infinitesimally small elements each of length A '. Each element is characterized by its x-coordinate. Figure 1 shows one such element of the string. We shall now obtain the equation of motion of such an element. In the equilibrium state, the forces acting on element AB are equal and opposite.
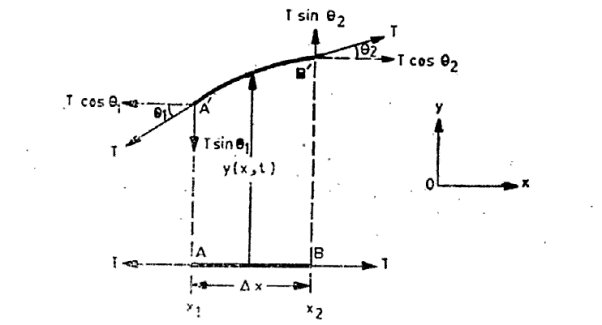
Figure 1: AB is an infinitesimal small element of string in the equilibrium position along x-axis. A’B’ is displaced position of the element.
The element is displaced along the y-axis to a new position A'B'. The element is no longer exactly straight; it has a slight curvature and the tension is tangential to the curve at A' and B'. If the displacement is small, the tension remains unchanged when the string is deformed.
Let y(x, t) be the transverse displacement of the element located at x at time t. When the string is released, the displacement of the element will change with time. Thus the displacement is a function of two variables x and t.
For an extremely small element (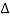 x
x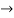 0) the net forces on the element along x and y directions are
0) the net forces on the element along x and y directions are
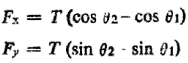
Where θ1 and θ2 are the directions of tangents to the string at the ends of the element, i.e. at x =x1 and x = x2 with x2—x1= 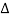 x.
x.
We are assuming that the transverse displacement is very small, so that θ1 and θ2 are small angles. We may, therefore, make the following approximations

The transverse component of tension on the element is, therefore, given by
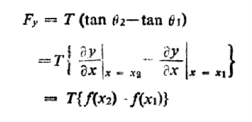 …………… (1)
…………… (1)
Where the function f(x) stands for 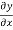 , Using Taylor’s series we have
, Using Taylor’s series we have
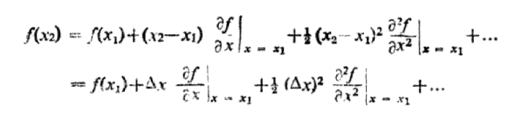
…………… (2)
We assume  x is small so
x is small so  x)2 and higher order can be ignored. Thus we may write
x)2 and higher order can be ignored. Thus we may write
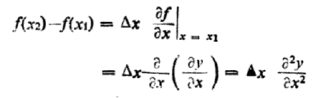 …………… (3)
…………… (3)
Where we have dropped the subscript x1 because, having ignored the higher order derivatives in Equation (2), it does not matter now where in the interval  x we evaluate the x-derivative.
x we evaluate the x-derivative.
Notice that the space derivative is written as a partial derivative because now the displacement y(x, t) is a function of two variables x and t. In a complete form we would write Equation (3) as
f(x2) — f(x1) = 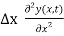 …………… (4)
…………… (4)
And Equation (1) as
Fy = 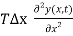 …………… (5)
…………… (5)
The equation of motion of the element is obtained from Newton's second law, namely, force = mass x acceleration.
Let μ be the linear density (mass per unit length) of the string. Therefore, the mass of the element of length 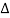 x = μ
x = μ 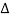 x
x
The acceleration of the element is 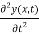
Hence Newton's force
μ 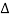 x
x 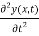
For dynamic equilibrium this force must balance the force fy given by equation (4). This gives the equation of motion of an element of the string, namely,
μ 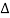 x
x 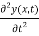 = T
= T 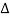 x
x 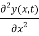 …………… (6)
…………… (6)
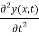 =
=
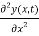 …………… (7)
…………… (7)
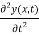 =
= 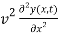 …………… (8)
…………… (8)
Where 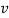 =
= 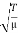 has dimensions of velocity so this is velocity of the wave.
has dimensions of velocity so this is velocity of the wave.
Equation (8) is a very famous second-order linear partial differential equation. It is called the classical wave equation.
We shall encounter this equation in many physical situations. The positive constant  (having dimensions of square of a velocity) is special to the string. In other physical situations, some other positive constant appears in its place in the wave equation. So far we have not explicitly stated which velocity the constant
(having dimensions of square of a velocity) is special to the string. In other physical situations, some other positive constant appears in its place in the wave equation. So far we have not explicitly stated which velocity the constant 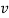 =
= 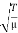 represents.
represents.
Every point on the string is moving with a time dependence of the form cosωt but that the amplitude of this motion is a function of the distance x of that point from the end of the string. Our assumed time dependence would require every point on the string to be instantaneously stationary at t = 0. If this is not so an initial phase angle must be introduced.
Thus we assume
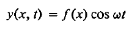 …………… (9)
…………… (9)
This then gives us
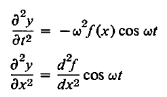 …………… (10)
…………… (10)
Since f(x) by definition is a function of x only, we can write 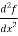 , instead of a partial derivative.
, instead of a partial derivative.
Substituting these derivatives in Equation (8) then gives us
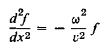 …………… (11)
…………… (11)
But this is the familiar differential equation satisfied by a sine or cosine function. Remembering that we have defined x = 0 as corresponding to one of the fixed ends of the string, with zero transverse displacement at all times, we know that an acceptable solution must be of the form
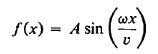 …………… (12)
…………… (12)
But we have the further boundary condition that the displacement is always zero at x = L. Hence we must also have
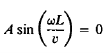 …………… (13)
…………… (13)
Hence
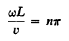 …………… (14)
…………… (14)
Where n is any (positive) integer. It will be convenient to introduce the number of cycles per unit time, v, equal to ω/2π. The frequencies of the permitted stationary vibrations are thus given by
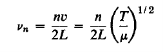 …………… (15)
…………… (15)
Where n, according to this calculation, may be 1, 2, 3, ... To infinity.
A vivid way of describing the shape of the string at any instant, in any particular mode n, is obtained by recognizing that the total length of the string must exactly accommodate an integral number of half-sine curves, as implied by Equation (14) We can therefore define a wavelength, associated with the mode n, such that
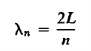 …………… (16)
…………… (16)
Then we can put
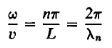 …………… (17)
…………… (17)
Hence, from Equation (12), the shape of the string in mode n is characterized by the following equation
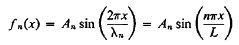 …………… (18)
…………… (18)
And the complete description of the motion of the string is thus as follows:
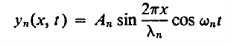 …………… (19)
…………… (19)
Where
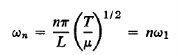 …………… (20)
…………… (20)
Since all the possible frequencies of a given stretched string are, according to the above analysis, simply integral multiples of the lowest possible frequency, ω1 a particular interest attaches to this basic mode—the fundamental.
It is the frequency of the fundamental that defines what we recognize as the characteristic pitch of a vibrating string, and which therefore defines for us the tension required to obtain a certain note from a string of given mass and length.
3 Question: Write a note Harmonic waves?
Solution:
The simplest normal mode, where the string vibrates in one loop, is labelled n = 1 and is called the fundamental mode or the first harmonic. The second mode (n = 2), where the string vibrates in two loops, is called the second harmonic. The nth harmonic consists of n vibrating loops. The set of all normal modes {n = 1, 2, 3, 4, 5, ... } is the harmonic spectrum. The spectrum of natural frequencies is { ω1, ω 2, ω3, ω4, ω5, ... }. Note that the frequency ω n of mode n is simply a whole-number multiple of the fundamental frequency: ω n = nω1.
The mode with three loops vibrates three times as fast as the mode with one loop. Harmonics are the basis of harmony in music. The sectional vibrations of a string as one whole, two halves, three thirds, and so on, are very special because these vibrations produce musical tones that sound the “most pleasant” when sounded together, i.e. they represent the most harmonious combination of sounds. This explains the origin of the word “harmonic”.
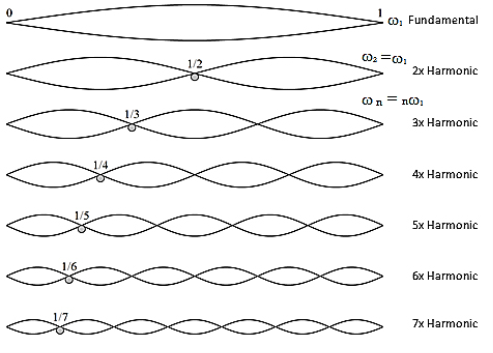
Figure 2: Harmonic waves
In a stringed instrument such as a piano, the string is struck once at some chosen point. At the moment of impact, and for a brief instant thereafter, the string is sharply pushed aside near this point, and its shape is nothing like a sine curve. Shortly thereafter, however, it settles down to a motion which is a simple super-position of the fundamental and a few of its lowest harmonics. It is a physically very important fact that these vibrations can occur simultaneously and to all intents independently of one another. Their mutual independence can be demonstrated by suddenly stopping the transverse motion of the string at a point that is a node for some harmonics but not for others.
Those component vibrations for which the point is a node will continue unaffected; the others will be quenched.
Thus, for example, if a piano string has been set sounding loudly by striking the key, which is kept held down, and the string is then touched one third the way along its length, all component vibrations are stopped except the third, sixth, etc., multiples of the fundamental frequency.
These Figures reveal that there are certain points on the string which are permanently at rest; the number of these points depends upon the number of the mode under study. These points are called nodes.
The points where the displacement is maximum are called antinodes.
It states that the frequencies of all the overtone of such a string are integral multiples of the fundamental frequency.
Overtones bearing this simple relation to the fundamental are called harmonics. The fundamental being first harmonic and it is called first overtone (twice the fundamental frequency ) being the second harmonic and so on.
4 Question: Derive reflection and transmission coefficients for a wave travels at a boundary?
Solution:
Let us suppose two waves string 1 and 2 of different linear densities are joined together to form a composite system. Let us suppose that both string have same tension T. The linear densities of the strings 1 and 2 are 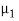 and
and 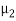 .
.
The wave velocities in strings 1 and 2 are given as
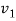 =
= 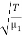 and
and 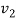 =
= 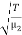
Let us suppose a wave (called the incident wave) is travelling in the +x direction on string 1. The particle d displacements of string 1 are given by, yi(x,t) = Ai sin (ωt—k1x)
Where k1 = 2π/λ1 = 2πν /v1 and Ai is the amplitude of the incident wave.
When this wave reaches the boundary (which we shall take at x = 0) separating the two strings, it is partly reflected and partly transmitted at the boundary. The reflected wave travels on string 1 in the negative x direction and the transmitted wave travels on string 2 in the positive x direction as shown n figure.
The particle displacements due to these waves are, therefore given by
yr(x,t) = Ar sin (ωt+k1x) …………. (1)
yt(x,t) = At sin (ωt—k2x)…………. (2)
Where k2 = 2π/λ2 = 2πν /v2 and Ar and At are the amplitudes of the reflected and transmitted waves respectively.
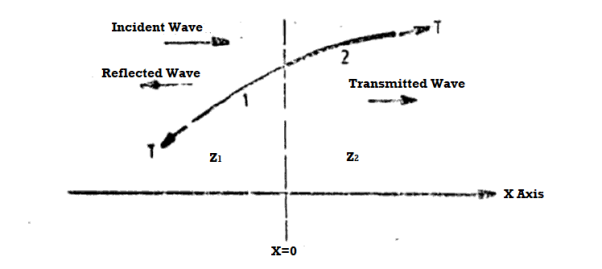
Figure 3: Reflection and transmission of waves at a boundary
Boundary conditions
The point x = 0 at the boundary undergoes oscillations under the combined influence of the incident and reflected waves in string 1. It then acts as a source of transmitted waves travelling in string 2. The boundary conditions to be satisfied at x = 0 are
(1) The displacement is the same immediately to the left and to the right of the boundary at x = 0, i.e. y(x, 0) is continuous across boundary at x = 0. Therefore, velocity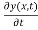 is also continuous.
is also continuous.
(2) The restoring force or transverse component of Tension [-T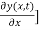 is continuous across the boundary at x = 0. To understand this, let us imagine that there is an infinitesimal element of mass at x = 0. If the gradient
is continuous across the boundary at x = 0. To understand this, let us imagine that there is an infinitesimal element of mass at x = 0. If the gradient 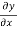 is not continuous, this would give rise to a net transverse force acting on this infinitesimally small mass of the string at x = 0. Consequently this element will have an infinite acceleration which is not permitted.
is not continuous, this would give rise to a net transverse force acting on this infinitesimally small mass of the string at x = 0. Consequently this element will have an infinite acceleration which is not permitted.
Recalling that y(x,t) in string 1 is due to a superposition of the displacement due to the incident and reflected waves and y(x,t) in string 2 is due only to the transmitted wave and using the boundary condition (1) we have
yi(x,t) + yr(x,t) = yt(x,t)…………. (3)
Ai sin (ωt—k1x) + Ar sin (ωt+k1x) = At sin (ωt—k2x) …………. (4)
Setting x=0 we have
Ai sin ωt + Ar sin ωt = At sin ωt
For all t, which gives
Ai + Ar = At …………. (5)
Boundary condition (2) requires that at x=0, we have
-T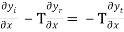 …………. (6)
…………. (6)
Or
Ai k1T cos (ωt—k1x) + Ar k1T cos (ωt+k1x) = At k2T cos (ωt—k2x)
Setting x=0 we have (for all t)
k1T (Ai - Ar) = k2T At…………. (7)
Now
k1T = 2πνT/v1 = 2πν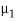
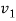 =2πν
=2πν 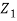 (
(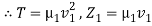 )
)
And
k2T = 2πν 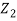
We then have
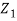 (Ai - Ar) =
(Ai - Ar) = 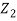 At
At
r12 = 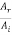 =
= 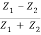 …………. (8)
…………. (8)
t12 = 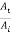 =
= 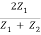 …………. (9)
…………. (9)
Where r12 and t12 are the reflection and transmission amplitude coefficients when a wave travels from string 1 to string 2. The ratio 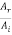 is the fraction of the incident amplitude reflected at the boundary and the ratio
is the fraction of the incident amplitude reflected at the boundary and the ratio 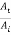 is the fraction of the incident amplitude transmitted across the boundary.
is the fraction of the incident amplitude transmitted across the boundary.
These fractions depend only on the impedances and are independent of the angular frequency ω of the incident wave. If the string is rigidly fixed at x = 0, say, by attaching this end to a wall, then the medium 2 is infinitely massive which means that 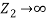 .
.
In this case 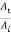 =0 giving
=0 giving 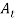 = 0 indicating that there is no transmitted wave and
= 0 indicating that there is no transmitted wave and 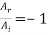 or
or 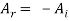 which means that the incident wave is completely reflected with a reversal in amplitude. The reversal of amplitude means a phase change of π on reflection.
which means that the incident wave is completely reflected with a reversal in amplitude. The reversal of amplitude means a phase change of π on reflection.
It is clear from equation (8) that if Z2 >Z1, the ratio 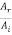 will be negative indicating a phase change of π on reflection. Thus we conclude that if a wave travelling in a medium of lower impedance meets the boundary of a medium of higher impedance (i.e. a medium in which the wave velocity is smaller), the wave reflected at the boundary undergoes a phase change of it.
will be negative indicating a phase change of π on reflection. Thus we conclude that if a wave travelling in a medium of lower impedance meets the boundary of a medium of higher impedance (i.e. a medium in which the wave velocity is smaller), the wave reflected at the boundary undergoes a phase change of it.
On the other hand if Z2< Z1 the ratio 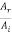 is positive. Thus, if a wave is reflected at the boundary of lower impedance (i.e. a medium in which the wave velocity is higher), the reflected wave does hot undergo any phase change.
is positive. Thus, if a wave is reflected at the boundary of lower impedance (i.e. a medium in which the wave velocity is higher), the reflected wave does hot undergo any phase change.
Furthermore, equation (9) shows that the ratio 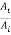 always remains positive independent of whether Z2 is less than or more than Z1. This shows that the transmitted wave does not undergo any phase change is illustrated in Figure 4 which shows reflection and transmission of a pulse at a boundary between two strings.
always remains positive independent of whether Z2 is less than or more than Z1. This shows that the transmitted wave does not undergo any phase change is illustrated in Figure 4 which shows reflection and transmission of a pulse at a boundary between two strings.
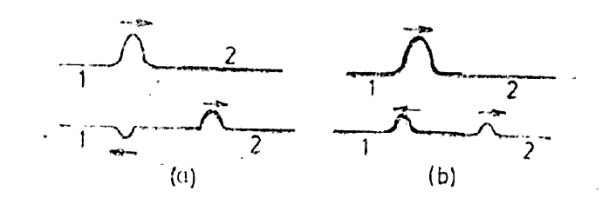
Figure 4: (a) Reflection and transmission of a pulse when string 2 has higher impedance. (b) Reflection and transmission of a pulse when string 2 has lower impedance.
If wave travels from string 2 to string 1 the r21 and t21 are the reflection and transmission amplitude coefficients
r21 = 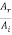 =
= 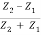 …………. (10)
…………. (10)
t21 = 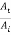 =
= 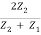 …………. (11)
…………. (11)
5 Question: Discuss the reflection and transmission coefficients of Energy at the Boundary?
Or
Prove that the rate at which energy arrives at the boundary with the incident wave is equal to the rate at which energy leaves the boundary with the reflected and transmitted waves.
Solution:
Reflection mid Transmission
Waves are a very useful mechanism for the transport of energy in a medium. It is interesting to consider what happens to the energy in a wave when it meets a boundary between two media of different impedances. As the wave travels along the string, each part of the string is thrown into harmonic oscillations with the passage of time.
We know that the rate at which energy is carried per unit length along the string is given by
P =  μvA2 ω2…………. (12)
μvA2 ω2…………. (12)
Let us now compute the rates at which energy is incident, reflected and transmitted at the boundary at x = 0. The rate of incident energy is the rate at which the energy is carried by the incident wave which is given by
Pi =  Z1Ai2 ω2…………. (13)
Z1Ai2 ω2…………. (13)
Similarly the rates of reflected and transmitted energies respectively are
Pr =  Z1Ar2 ω2…………. (14)
Z1Ar2 ω2…………. (14)
Pt =  Z2At2 ω2…………. (15)
Z2At2 ω2…………. (15)
Using Equations (8) and (9) we find that
Pr =  Z1(
Z1(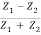 ) ω2 Ai2…………. (16)
) ω2 Ai2…………. (16)
Pt = 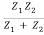 ω2 Ai2…………. (17)
ω2 Ai2…………. (17)
And
Pr + Pt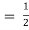 Z1ω2 Ai2 (
Z1ω2 Ai2 (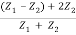 )=
)=  Z1ω2 Ai2 = Pi…………. (19)
Z1ω2 Ai2 = Pi…………. (19)
In other words, the rate at which energy arrives at the boundary with the incident wave is equal to the rate at which energy leaves the boundary with the reflected and transmitted waves. This is consistent with the conservation of energy at the junction of two media. Thus, energy is conserved. All the energy arriving at the boundary with the incident wave leaves the boundary with the reflected and transmitted waves. This is expected since we have assumed that there is no absorption of energy at the boundary. The reflection and transmission energy coefficients are given by
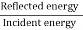 =
= 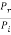 =
= 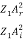 =
= 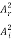 = (
= (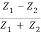 )2
)2
 =
= 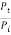 =
= 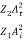 =
= 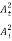 =
= 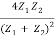
Reflection coefficient +Transmission coefficient = 1
Also if Z1 = Z2, no energy is reflected and the impedances are said to be matched.
6 Question: Discuss Impedance matching?
Or
Prove that the impedance of the coupling medium is the harmonic mean of the two impedances to be matched
Solution:
Impedance matching represents a very important practical problem in the transfer of energy. Long distance cables carrying energy must be accurately matched at all joints to avoid wastage from energy reflection. The power transfer from any generator is a maximum when the load matches the generator impedance. A loudspeaker is matched to the impedance of the power output of an amplifier by choosing the correct turns ratio on the coupling transformer. This last example, the insertion of a coupling element between two mismatched impedances, is of fundamental importance with applications in many branches of engineering physics and optics. We shall illustrate it using waves on a string, but the results will be valid for all wave systems.
We have seen that when a smooth joint exists between two strings of different impedances, energy will be reflected at the boundary. We are now going to see that the insertion of a particular length of another string between these two mismatched strings will allow us to eliminate energy reflection and match the impedances.
In Figure (5) we require to match the impedances Z1= ρ1c1 and Z3 = ρ3c3 by the smooth insertion of a string of length l and impedance Z2= ρ2c2. Our problem is to find the values of l and Z2.
The incident, reflected and transmitted displacements at the junctions x = 0 and x = l are shown in Figure 5 and we seek to make the ratio
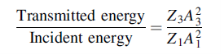
Equal to unity.
The boundary conditions are that y and T 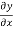 are continuous across the junctions x = 0 and x =l.
are continuous across the junctions x = 0 and x =l.
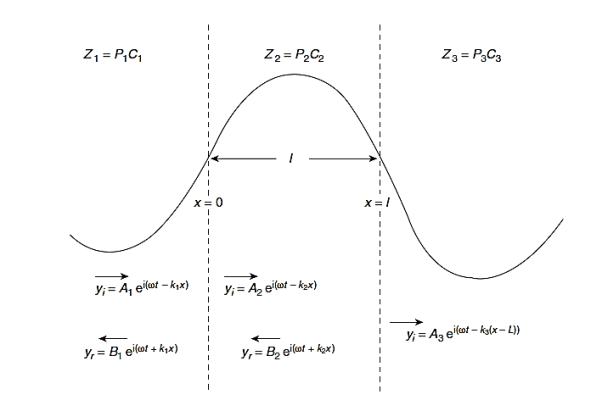
Figure 5: The impedances Z1 and Z3 of two strings are matched by the insertion of a length l of a string of impedance Z2. The incident and reflected waves are shown at boundary x=0 and x=l. The impedances are matched when 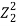 = Z1Z3 and for l= λ/4 in Z2, results which are true for waves in all media
= Z1Z3 and for l= λ/4 in Z2, results which are true for waves in all media
Between Z1 and Z2 the continuity of y gives
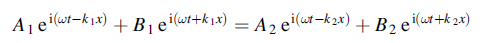
Or
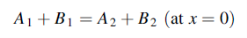 ……………(1)
……………(1)
Similarly the continuity of T 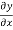 at x=0 gives
at x=0 gives
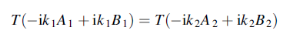
Dividing this equation by ω and remembering that
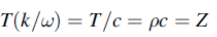
We have
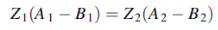 ……………(2)
……………(2)
Similarly at x= l, the continuity of y gives
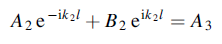 ……………(3)
……………(3)
And the continuity of T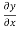 gives
gives
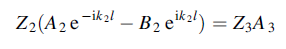 ……………(4)
……………(4)
From the four boundary equations (1), (2), (3) and (4) we require the ratio A3=A1.using above equations
We use equations (1) and (2) to eliminate B1 and obtain A1 in terms of A2 and B2. We then use equations (3) and (4) to obtain both A2 and B2 in terms of A3. Equations (1) and (2) give
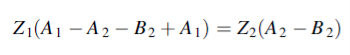
Or
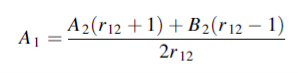 ……………(5)
……………(5)
Where
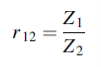
Equations (3) and (4) give
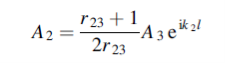 ……………(6)
……………(6)
And
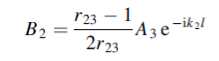
Where
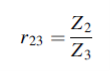
Where equation (5) and (6) gives
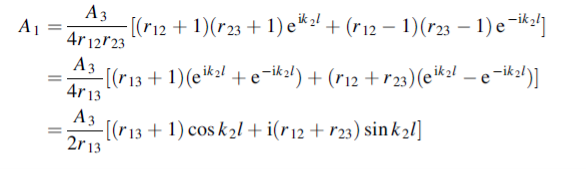
Where
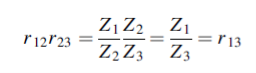
Hence
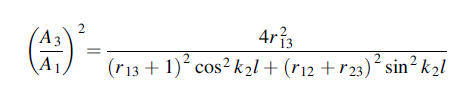
or
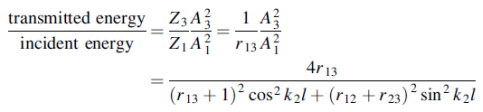
If we choose
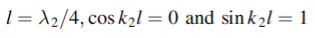
We have
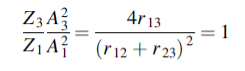
When r12 =r23
That is when
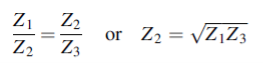
We see, therefore, that if the impedance of the coupling medium is the harmonic mean of the two impedances to be matched and the thickness of the coupling medium is
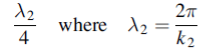
All the energy at frequency ω will be transmitted with zero reflection. The thickness of the dielectric coating of optical lenses which eliminates reflections as light passes from air into glass is one quarter of a wavelength. The ‘bloomed’ appearance arises because exact matching occurs at only one frequency. Transmission lines are matched to loads by inserting quarter wavelength stubs of lines with the appropriate impedance.
7 Question: Explain standing waves on a String of fixed length?
Solution:
Standing Waves on a String of Fixed Length
Consider a string of length L stretched with a tension T along the x-axis with its ends at A (x= 0) and B(x = L) rigidly fixed (Figure 6). A transverse wave is produced by creating a harmonic disturbance near the end A. The wave travels along the string in the +x direction and gets reflected at end B which travels in –x direction. The interference between two oppositely travelling wave ends gives rise to standing wave on the string. Let us consider the simplest case of a monochromatic incident wave of a single frequency co and amplitude Ai. The displacement at time t of a particle, say C, 1ocated at x due to the incident wave travelling in the +x direction is given by
yi(x,t) = Ai sin (ωt—kx) = Ai sin {k(vt—x)}…………..(1)
Where k = 2π/λ, λ is the wavelength of the wave, v =ω/k is velocity of the wave
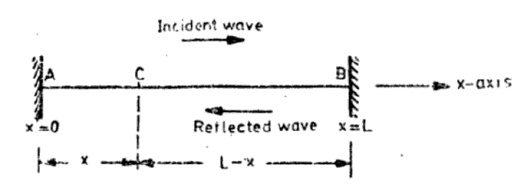
Figure 6: Standing waves on a string fixed at both ends x = 0 and x = L
Let us find out the displacement at time t of the same particle C located at x due to the wave reflected from the fixed end B.
The reflected wave can be written as
yr(x,t) = Ar sin {k(vt—x’)}…………..(2)
Where Ar, is the amplitude of the reflected wave and x’ must be the distance travelled by the wave of equation (1) from A to R and then to C, i e. x’ = x-(L-x)= 2L-x.
Hence the displacement at time t of particle C at x due to the reflected wave must be given by
yr(x,t) = Ar sin {k(vt+x-2L)}
The sine function involves (vt+x) which represents a wave in the - x direction, the direction of propagation of the wave reflected at B.
From the principle of superposition, the resultant displacement at time t at any point x is given by
y(x,t) = yi(x,t) + yr(x,t)
= Ai sin {k(vt—x)} + Ar sin {k(vt+x-2L)}…………..(3)
Since the ends x 0 and x = L are rigidly fixed, boundary conditions are (i) y = 0 at x = 0 and (ii) y = 0 at x =L. Using condition (II) in Eq. (8.7) gives
0 = Ai +sin {k(vt—L)} + Ar sin {k(vt-L)}
0=(Ai + Ar) sin {k(vt—L)}…………..(4)
Which is satisfied for all t values
Ai + Ar =0
Ar = - Ai =-A
The reversal of the amplitude of the reflected wave implies a phase change 1800 on reflection at the rigid end x = L. Putting Ar = - Ai =-A in equation (3) we have
y(x,t) = A {sin k(vt—x) - sin k(vt+x-2L)}
We know that  = 2
= 2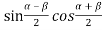 using this identity, we get
using this identity, we get
y(x,t) = 2A {sin k(L—x) cosk(vt -2L)}…………..(5)
At x=L equation (5) gives y=0, which is true since end is rigid so there is no resultant motion.
The first boundary conditions, namely y=0 also at x=0 remains to be satisfied.
Put x=0 in equation
(5) require y to be zero at all values of t.
SinkL =0
KL =0,π, 2π, 3π……..
knL = 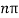
kn = 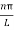 where n is an integer 0,1,2,3,…..…………..(6)
where n is an integer 0,1,2,3,…..…………..(6)
The allowed frequencies are ω =kv
ωn =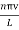 …………..(7)
…………..(7)
νn =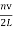 =
= 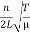 …………..(8)
…………..(8)
Using equation (5) and (6) we get
y(x,t) = 2A {sin 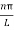 (L—x) cos
(L—x) cos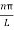 (vt -L)}
(vt -L)}
y(x,t) = -2A (sin 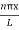 cos
cos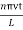 )…………..(9)
)…………..(9)
Equation (9) can be written as
y(x,t) = -2A (sinknx cosωnt )…………..(10)
Equation (9) is the equation of a standing or stationary wave. It is obvious that this equation does not represent a travelling wave since it no longer has the characteristic form involving (ωt–kx) or (ωt+kx) in the argument of the trigonometric function.
Modes of Vibration
Notice that the frequencies given by equation (8) are just the frequencies of the normal modes of a string fixed at both ends.
The mode with n = 0 is unphysical since then ν = 0 implying that there is no vibration at all. The mode with n = 1 is called the fundamental mode. The frequency and particle displacements in this mode are given by
ν1 = 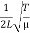
y(x,t) = -2A (sin 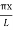 cos
cos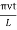 )
)
Notice that the points x = 0 and x = L are permanently at rest. These points on the string are called nodal points or nodes. But the point x = 1/2 has a maximum displacement. These points are called antinodes. Figure (7) shows the particle displacement in the fundamental mode.
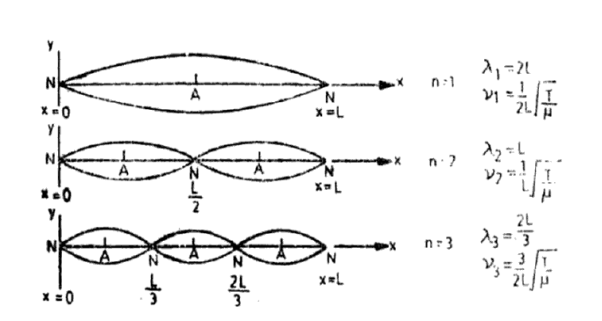
Figure 7: Standing Waves on a string of length L fixed at both ends Modes of string: first three harmonics n = 1, 2 and 3.
The mode with n= 2 is called the second harmonic. The frequency and particle displacements in this mode are given by
ν2 = 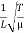 = 2 ν1
= 2 ν1
y(x,t) = -2A (sin 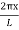 cos
cos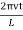 )
)
Notice that, in addition to nodes at x=0 and x=L, there is another node at x= L/2. The antinodes are at, L/4, 3L/4. This mode is shown in Figure 7(b). Figure 7(c) shows the third harmonic.
We find that in the nth harmonic there are (n—1) positions (between the fixed ends) equally spaced along the string where the displacement is always zero. These points marked N are the nodes in a standing wave pattern.
8 Question: Derive wave equations for longitudinal vibrations of a rod?
Solution:
Longitudinal vibrations of a rod
Consider a cylindrical metal rod of uniform cross-sectional area. When the rod is struck lengthwise (or stroked) it begins to vibrate. The vibrations are in the audible range of frequencies. Let us obtain the equation of motion of the particles of the rod.
Suppose the rod is lying along the x-axis. We divide the rod into a large number of small slices each of length, say,  x.
x.
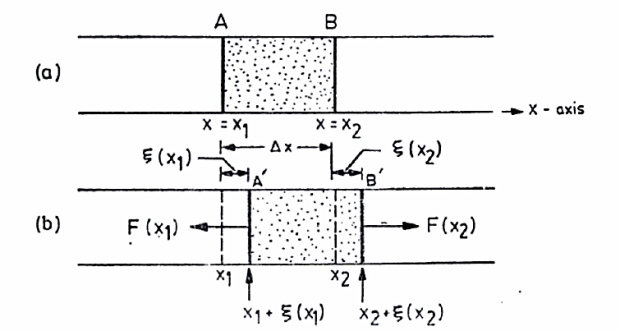
Figure 8: Longitudinal vibrations of a rod (a) Equilibrium State (b) Disturbed State
Consider one such slice or element AB as shown in Figure. The particles at the end A are at a distance of x1 = x from some origin and those at end B are at a distance x2 = x+ x.
x.
When the rod is struck lengthwise the particles of the rod are displaced along the x-axis, i.e. along the length of the rod. In other words, the particle displacements are longitudinal rather than transverse as in the case of a string.
We shall use the symbol ξ to denote the displacement, along the x-axis, of the particles in a plane at x = xi perpendicular to the axis of the rod. We shall now obtain the equation of motion of a thin slice AB of the rod which, in the undisturbed state, is contained between x and x+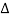 x as shown in Figure 8(a).
x as shown in Figure 8(a).
Figure 8(b) shows the displaced position of the slice. Let the x-coordinate of the end A of the slice in the displaced position be x1 +ξ (x1) so that ξ (x1) represents the displacement of the particles at the plane x1. Similarly let x2 +ξ (x2) be the x-coordinate the particles originally located at a plane x = x2 so that ξ (x2) is the displacement of the particles at the plane x2.
Therefore, Change in length of the slice
= ξ (x2) - ξ (x1)
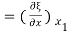
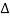 x
x
Where we have used Taylor's expansion
ξ (x2) = ξ (x1) + 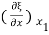
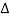 x +………
x +………
And retained terms up to order (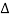 x) as in the case of a string. Since the original length of the slice is
x) as in the case of a string. Since the original length of the slice is 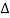 x. The longitudinal strain Ɛ at x1 is given by
x. The longitudinal strain Ɛ at x1 is given by
ξ (x1) = 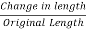 =
= 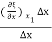 =
= 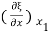
If Y is the young’s modulus of the material of the rod, the stress S at x1 is given by
S(x1) = Y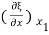
Similarly the stress at x2 is given by
S(x2) = Y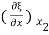
The net stress on the element AB is
S(x2) - S(x1) = Y [f(x2)-f(x1)]
Where f(x) =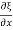 Since f(x2) - f(x1) =
Since f(x2) - f(x1) = 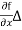 x, we have
x, we have
S(x2) - S(x1) = Y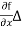 x, we have
x, we have
= Y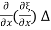 x
x
= Y 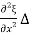 x
x
If 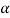 is a cross sectional area of the rod, net longitudinal force on the element is given by
is a cross sectional area of the rod, net longitudinal force on the element is given by
F(x)= F(x2) - F(x1) =Stress x Area = Y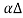 x
x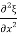
To obtain the equation of motion, we apply Newton's law to the slice. If ρ is the density of the rod, the mass of the slice is ρ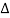 x. Therefore, Newton's force F' is mass x acceleration, i.e.
x. Therefore, Newton's force F' is mass x acceleration, i.e.
F’ = ρ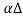 x
x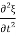
In dynamic equilibrium, the two force F and F’ must balance, giving
ρ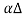 x
x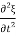 = Y
= Y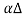 x
x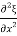
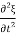 =
= 
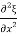
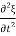 =
= 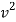
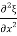
With  =
= 
Notice that  has the dimensions of a velocity will be identified as the velocity of longitudinal (is sound) waves travelling in the rod
has the dimensions of a velocity will be identified as the velocity of longitudinal (is sound) waves travelling in the rod
As the wave travels along the rod, different particles acquire a displacement ξ (x, t) which is a function of both x and t. It may be remarked that the picture presented above is a crude one because the particles of the rod are bouncing back and forth due to thermal agitation, even when there is no sound. The quantity ξ (x, t) actually measures the average displacement, due to sound wave, of those particles whose average position was originally at x.
9 Question: Explain sound wave? Derive formula for speed of wave?
Solution:
Longitudinal waves propagate as sound waves in all phases of matter, plasmas, gases, liquids and solids, but we shall concentrate on gases and solids. In the case of gases, limitations of thermodynamic interest are imposed; in solids the propagation will depend on the dimensions of the medium. Neither a gas nor a liquid can sustain the transverse shear necessary for transverse waves, but a solid can maintain both longitudinal and transverse oscillations.
The wave we analyse here is sound in an elastic medium, such as air. Let’s consider a one dimensional wave travelling in the x direction. We’ll consider a section with cross section A. Let us suppose a wave travelling through a pipe, and neglect the viscous and thermal interactions at the wall. We’ll consider some point here to analyse sound propagation:
- First, look at how spatial variations in displacement produce compression or expansion and thus derive how the pressure depends on displacement.
- Second, we’ll apply Newton’s second law to see how spatial variations in pressure accelerate the air, and thus change the displacement.
First we will analyse how displacement affects pressure
Let us consider the motion of an element of our medium, whose position, when there is no sound wave disturbance, is between x1 and x2. We’ll make the distance between x1 and x2 much less than a wavelength of sound.
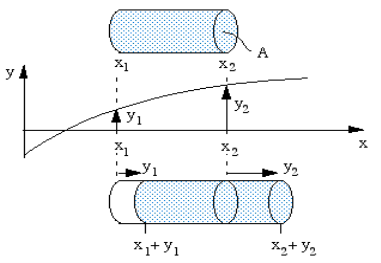
Figure 9: Wave travelling through a pipe
So the undisturbed volume of this element is
V = A(x2 – x1)
And, using the density ρ and cross section A, its mass is
m = ρV = ρA(x2 − x1) ………… (1)
Let y is the average displacement of the molecules in the x direction at any time
y is written as average displacement because in gas, the individual molecules have their own random motion superimposed on the average or bulk motion that we are going to observe.
At some time t, medium show displacement. It is displaced from its equilibrium position such that the medium whose equilibrium position is at x1 is moved to x1 + y1 and the medium whose equilibrium position is at x2 is moved to x2 + y2.
The new volume of our element of air is
V + δV = A(x2 + y2 − x1 − y1) and, using (1), we have
δV = A(y2 − y1).
When a medium is compressed, its pressure rises. The ratio between the pressure increase p and the proportional volume reduction is called the volumetric modulus of elasticity 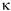 , defined by
, defined by
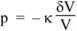
So the pressure in our element, when it is displaced as shown in above diagram, is
 , so
, so 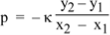
In the limit where x2 – x1 is very small, this gives us the relation between displacement y and pressure p:
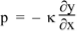 …………(2)
…………(2)
Now to apply Newton’s second law. The absolute pressure at x1 is PAtm + p1, where PAtm is undisturbed atmospheric pressure. So the pressure on the left, acting on area A, exerts a force to the right of (PAtm + p1)A. Similarly, at x2, the force on the right, acting to the left, is (PAtm + p2)A. So the net force to the right is
F = (p1 − p2)A.
Let’s take the average displacement of our element as y (where y1 < y < y2). So, taking the second derivative with respect to time, its acceleration to the right is
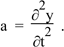
Equation (1) gives the mass and the two equations above give F and a, so F = ma becomes
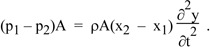
We rearrange, reverse the order of p1 and p2 and cancel A to give
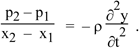
In the limit of very small distance x2 – x1, this gives
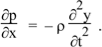
This is the wave equation.
Equation (2) gave us 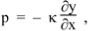 so combining this with the equation above we have
so combining this with the equation above we have
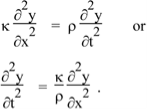 (3)
(3)
One dimensional wave equation. In case of a string with tension T and linear density μ, we had
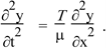
We showed then that this has wave solution with speed 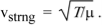
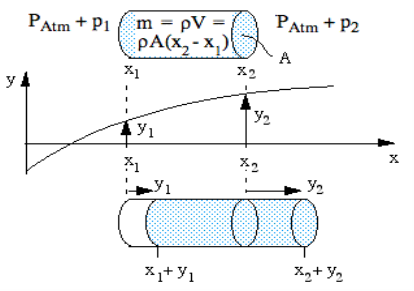
Figure 10: Wave travelling through a pipe under pressure
The solution is given by
y = ym sin (kx − ωt)
And take derivatives, we have
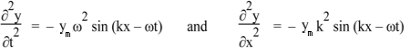
From the above solution it is given that (ω/k)2 =  /ρ. Now ω/k is the wave speed so we have, for the speed of sound:
/ρ. Now ω/k is the wave speed so we have, for the speed of sound:
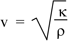
The tension in the string provides a restoring force; so does the elasticity of the medium here. The inertia was provided by the mass per unit length μ of the string, here by the mass per unit volume ρ of the medium.
Although we imagined that our element was air, we have so far only assumed that it is elastic. So this equation is true for longitudinal waves in any elastic medium. For air, we can give a value for the elastic modulus  .
.
Let us discuss the case of ideal gas. We show that, during adiabatic expansion and compression, the pressure P and volume V are related
PVγ = constant
Where γ is the adiabatic constant, or the ratio of the specific heat at constant pressure to the specific heat at constant volume, which is about 1.4 for air. Taking natural logs of both side, we have
Ln P + γ ln V = constant.
Taking derivatives gives us
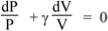
So 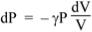
The definition of the bulk modulus, expressed as a differential, is
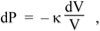
So combining the two equations above we have
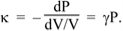
So the speed of sound in an ideal gas is
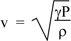
For air at atmospheric pressure (P = 101 kPa) and at T = 20 °C, the density is 1.20 kg.m−3. Taking γ = 1.4 gives a speed of sound of 343 m.s−1.
Specific acoustic impedance
Let’s relate the velocity and pressure, using the solution above:
y = ym sin(kx − ωt)
The particle velocity is
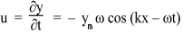
Using equation (2), we have
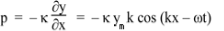
The specific acoustic impedance z of a medium is defined by p/u, so, using the equations above
z = κk/ω.
Above, we had κ/ρ = v2, above so κ = ρv2. We also had ω/k = v. Substituting these gives the specific acoustic impedance
z = ρv.
10 Question: A string of length l = 0.5 m and mass per unit length 0.01 kgm-1 has a fundamental frequency of 250 Hz. What is the tension in the string?
Solution:
We have
ν =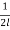
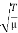
Or T = 4l2 ν2 μ = 4 × (0.5)2 × (250)2 × 0.01
= 625 N.
11 Question: A steel wire is stretched between two clamps 100 cm apart with a tension winch produces an extension of 0.608 cm in it. Calculate the fundamental frequency of its transverse vibration Density of steel = 7600 kgm-3, and its Young's modulus = 2x1011 Nm-2. Winch overtone of the string will correspond to a frequency of 800 Hz?
Solution:
Let L be the length of the wire and 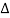 L the extension produced when it is stretched with a tension T. Then Y, the Young's modulus of the wire is given by
L the extension produced when it is stretched with a tension T. Then Y, the Young's modulus of the wire is given by
Y = 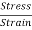 =
= 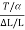 =
= 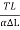
Where 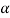 it the cross-sectional area of the wire. Thus
it the cross-sectional area of the wire. Thus
T = 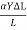 ………….(1)
………….(1)
Now the fundamental frequency of the wire is given by
ν1 = 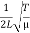 ………….(2)
………….(2)
But 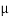 =mass per unit length, =
=mass per unit length, =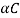 where
where 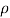 is the density of the wire.
is the density of the wire.
Using this 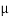 and Eq. (1) in Eq. (2), we get
and Eq. (1) in Eq. (2), we get
ν1 = 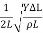
Putting the numerical values (In SI units), we have
ν1 = 200 Hz
Evidently the fourth harmonic (or the third overtone) has a frequency of 800 Hz.
12 Question: Two wires of radii r and 2r respectively are welded together end to end. This combination is used as a sonometer wire kept under tension T. The welded point is midway between the two bridges. What would be the ratio of the number of loops formed in the wires such that the joint is a node when stationary vibrations are set up in the wires?
Solution
Let n1 and n2 be the number of loops formed in the wires of radii r and 2r respectively.
Then
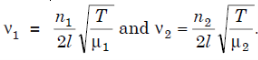
Since the welded wire is continuous, ν1 = ν2 and
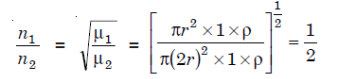
Where ρ = density of the material of the wires.