Question Bank ( unit-2)

                             Question Bank ( unit-2)

                             Question Bank ( unit-2)

Question-1: find the linear transformation of the matrix A.

                                     A =

Sol. We have,

                                   A =

Multiply the matrix by vector x = (x , y , z) , we get

                                   Ax =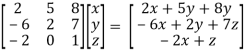

                                        = ( )

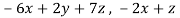f(x , y , z) = ( )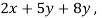

Which is the linear transformation of A.

Question-2: Are the vectors , , linearly dependent. If so, express x1 as a linear combination of the others.

Solution:

Consider a vector equation,

i.e.

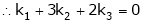
Which can be written in matrix form as,

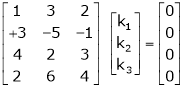
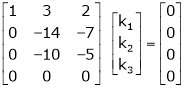
Here & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,

Put

and

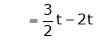
Thus

i.e.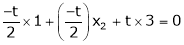

i.e.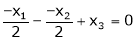

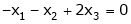
Since F11 k2, k3 not all zero. Hence are linearly dependent.

Question-3: At what value of P the following vectors are linearly independent.

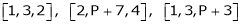
Solution:

Consider the vector equation.

i.e.

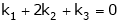
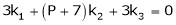
This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.

If and only if Determinant of coefficient matrix is non zero.

consider .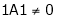

.

i.e.

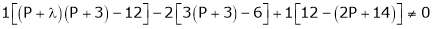
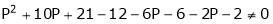
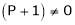
Thus for 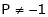the system has only trivial solution and Hence the vectors are linearly independent.

Question-4: Determine the eigen values of eigen vector of the matrix.

Solution:

Consider the characteristic equation as,

i.e.

i.e.

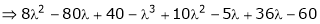
i.e.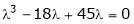

Which is the required characteristic equation.

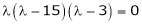
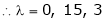are the required eigen values.

Now consider the equation

… (1)

Case I:

If 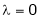Equation (1)becomes

R1 + R2

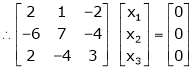
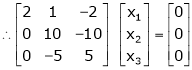
Thus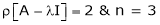

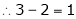independent variable.

Now rewrite equation as,

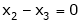
Put x3 = t

&

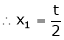
Thus .

Is the eigen vector corresponding to .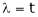

Case II:

If equation (1) becomes,

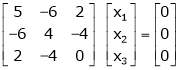
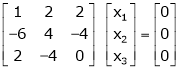
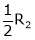
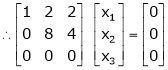
Here

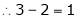independent variables

Now rewrite the equations as,

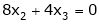
Put

&

.

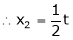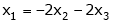
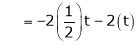
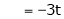
Is the eigen vector corresponding to .

Case III:

If equation (1) becomes,

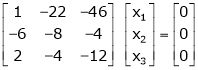
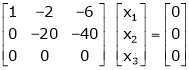
Here rank of

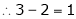independent variable.

Now rewrite the equations as,

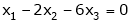
Put

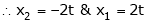
Thus .

Is the eigen vector for .

Question-5: :  Diagonalise the matrix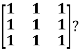

Sol.

Let A=

The three Eigen vectors obtained are  (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values .

Then 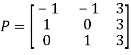   and

Also we know that    

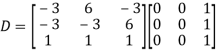
Question-6: Diagonalise the matrix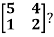

Sol.

Let A =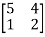

The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values .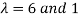

Then    and also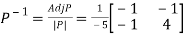 

Also we know that    

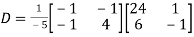
Question-7: Find the characteristic equation of the matrix A =   and Verify cayley-Hamlton theorem.

Sol. Characteristic equation of the matrix, we can be find as follows-

Which is,

( 2 -  , which gives

According to cayley-Hamilton theorem,

  …………(1)

Now we will verify equation (1),

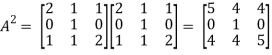
Put the required values in equation (1) , we get

Hence the cayley-Hamilton theorem is verified.

Question-8: Find the characteristic equation of the the matrix A and verify Cayley-Hamilton theorem as well.

                                           A =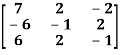

Sol. Characteristic equation will be-

                   = 0

( 7 -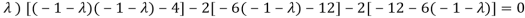

(7-

(7-

Which gives,

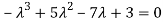
Or

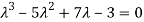
According to cayley-Hamilton theorem,

   …………………….(1)

In order to verify cayley-Hamilton theorem , we will find the values of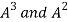 

So that,

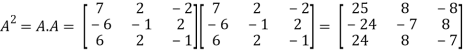
Now

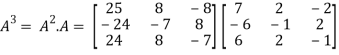
Put these values in equation(1), we get

= 0

Hence the cayley-hamilton theorem is verified.

Question-9: Find the inverse of matrix A by using Cayley-Hamilton theorem.

                                                 A =

Sol.  The characteristic equation will be,

                                                 |A - 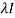| = 0

Which gives,

                 (4-

According to Cayley-Hamilton theorem,

Multiplying by 

That means

On solving ,

11

           = 

          = 

So that,

Question-10: Find the inverse of matrix A by using Cayley-Hamilton theorem.

                                            A =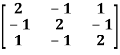

Sol.  The characteristic equation will be,

                                                 |A - | = 0

                                          = 

                                         = (2-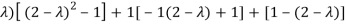

                                        = (2 -

                                       =

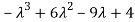
That is,

Or

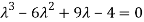
We know that by Cayley-Hamilton theorem,

…………………….(1)t,

Multiply equation(1) by 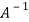, we get

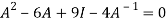
Or

Now we will find 

=

=

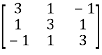
Hence the inverse of matrix A is,

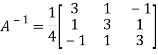
Question-11: : Find 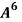  of matrix A by using Cayley-Hamilton theorem.

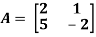
Sol. First we will find out the characteristic equation of matrix A,

                                 |A - 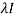| = 0

We get,

Which gives,

               (

We get,

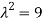
Or              I  ……………………..(1)

In order to find find 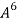we take cube of eq. (1)

We get,

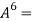                      729I                            we know that-  

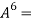                    729                       we know that- value of I =

Question-12: find out the quadratic form of following matrix.

                                               A =

Solution:  Quadratic form is,

                                                      X’ AX

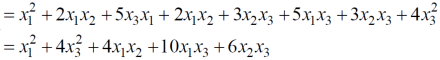
Which is the quadratic form of a matrix.

Question-13: find the real matrix of the following quadratic form:

   Sol.  Here we will compare the coefficients with the standard quadratic equation,

         We get,

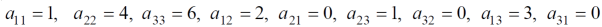
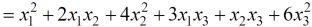
Question-14: Find the orthogonal canonical form of the quadratic form.

                                5

Sol. The matrix form of this quadratic equation can be written as,

                             A =

We can find the eigen values of A as –

                             |A - 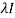| = 0

                    = 0

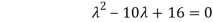
Which gives,

The required orthogonal canonical reduction will be,

                                           8 .