Question Bank(unit-4)
Question Bank(unit-4)
Question-1: Verify Rolle’s theorem for the function f(x) = x(x+3)
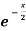
Sol. First we will differentiate the given function with respect to x, we get
f’(x) = (x²+3x) 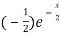 + (2x + 3)
+ (2x + 3)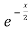
= 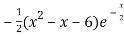
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.
Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).
Here f(x) satisfies all the conditions of Rolle’s theorem,
Then,
f’(x) = 0 , which gives
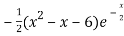 = 0
= 0
We get,
X = 3 and x = -2
Here we can see that clearly -3<-2<0 , therefore there exists -2 ∈ (-3,0) such that
f’(-2) = 0
That means the Rolle’s theorem is true for the given function.
Question-2: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Sol. (1)
As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+  and 2 -
and 2 - 
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Question-3: Verify the Rolle’s theorem for sin x in the interval [ ]
]
Sol. Suppose f(x) = sin x
We know that sin x is continuous for all x.
Now , f’(x) = cos x exists for all x in (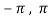 ) and
) and
f( 0
0
f( 0
0
Thus f(x) satisfies all the conditions of Rolle’s theorem.
Now,
f’(x) = 0 that gives , cos x = 0
x = 
Here we notice that both intervals lie in ( .
.
There exists, c = 
So that, f’(c) = 0
The Rolle’s theorem has been verified.
Question-4: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) =  =
=  =
=  = 3
= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2 
Here we see that the value of c lies between 0 and 4
Therefore the given function is verified.
Question-5: Verify Lagrange’s mean value theorem for f(x) = log x in [1,e].
Sol. We already know that the function which is log x is continuous for all x>0.
So that this is the continuous function In [1,e]
Now,
f’(x) = 1/x
Which is exists for all x in (1,e)
So that f(x) is differentiable in (1,e).
By Lagrange’s mean value theorem, we get
f’(c) =  , let x = c,
, let x = c,
then ,
f’(c) = 
We get,
c = e-1
e-1 will always lies between 1 and e .
Hence the function is verified by Lagrange’s mean value theorem
Question-6: Verify Cauchy’s mean value theorem for the function f(x) = sin x and g(x) = cos x in [ 0 , π/2]
Sol. It is given that ,
f(x) = sin x and g(x) = cos x
now ,
f’(x) = cos x and g’(x) = - sin x
We know that both the functions are continuous in [ 0 , π/2] and differentiable in ( 0 , π/2 )
Also , g’(x) = -sin x ≠ 0 for all x ϵ( 0 , π/2 )
By Cauchy’s mean value theorem , we get
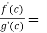
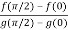 for some c: 0< c <
for some c: 0< c < 
That means
 which gives,
which gives,
Cot c = 1
C = 
Now we see that  lies between 0 and
lies between 0 and 
Question-7: Find the Taylor’s series for the function f(x) = 3x² - 6x + 5 in ascending powers of x-3.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) + 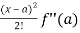 + ………
+ ……… . ………….(1)
. ………….(1)
Here ,
f(x) = 3x² - 6x + 5 and a = 3. So that f(a) = 14
Now , we will find out the derivatives ,
f’(x) = 6x – 6 and f’(3) = 12
f’’(x) = 6 and f’’(3) = 6
f’’’(x) = 0 and f’’’(x) = 14
Put these values in Taylor’s theorem, we get
3x² - 6x + 5 = 14 + 12(x-3) + 6 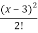 +…………. Ans.
+…………. Ans.
Question-8: Determine the area under the curves y = 2x² + 10 and y = 4x + 16.
Sol. Here we will find out the intersection, which are the boundaries of the curve,
2x² + 10 = 4x + 16
2x² - 4x – 6 = 0
2 (x + 1) ( x – 3 ) = 0
We get, x = -1 and x = 3,
We know that, Area under the curve,
A = 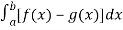

Question-9: A force of 1200 N compresses a spring from its natural length of 18 cm to a length of 16 cm. How much work is done in compressing it from 16 cm to 14 cm?
Sol. Here,
F = kx
So that,
1200 = 2k
K = 600 N/cm
In that case,
F = 600x
We know that,
W = 
W =  , which gives
, which gives
W = 3600 N.cm
Question-10: using slicing method, find out the volume of solid of revolution bounded by f(x) = x² - 4x +5 , x = 1 and x = 4, rotated about the x-axis.
Sol. Intervals are given. [ 1 , 4]
Here the solid is formed by revolving the region about x-axis , the cross – sections are circle .
Area of the cross section is , then is the area of circle, here radius of the circle is given by f(x).
We know that,
Area of the circle= π r²
= π [f(x)]²
= π[x² - 4x +5]²
Volume will be,
V = 
= 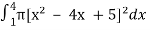
= 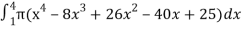 which gives,
which gives,
=  π
π
So the volume is 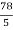 π
π
Question-11 Find the volume of the solid of revolution generated by rotating the region between the graph of f(x) = √x over the interval [1,4] around x-axis.
Sol. The graph of the function will look like as follow,

On rotation it will make circle ( cross-section)
We know that,
V = 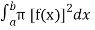
=  =
= 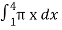 , which gives
, which gives
= 
The volume is 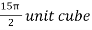
Question-12: suppose a wire hanging on two poles follows the curve,
f(x) = a cosh(x/a)
Find the length of the wire.
Sol. We will find the first derivative of f(x),
f’(x) = sinh(x/a)
The curve of f(x) will look like,
Hence the curve os symmetric, we will measure the length of one side first,
The limits on one side will be, 0 to b
We know that
Length of Arc = 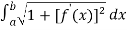
Put f’(x) = sinh(x/a), we get
Length of Arc = 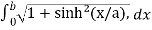
Use the identity,

= 
= 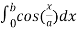
We get on solving,
a sinh(b/a)
On both sides, the length of the curve will be,
2 a sinh(b/a)
Question-13: find the surface of the surface generated by revolving the graph f(x) =  over the interval [1,4] around x-axis.
over the interval [1,4] around x-axis.
Sol. The graph of the function will look like

f(x) = 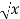 then f’(x) = 1/2 (
then f’(x) = 1/2 (
(f’(x))² = 1/4x
Then,
S = 
S = 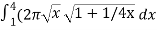
S = 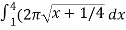 ,
,
Let u =  , then du = dx, when x = 1 , u = 5/4 and when x = 4 , u = 17/4,
, then du = dx, when x = 1 , u = 5/4 and when x = 4 , u = 17/4,
This will give,
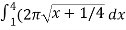 =
= 
On solving the integral we get,
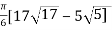 = 30.84 (approx.)
= 30.84 (approx.)
Question-14: Show that 

Solution : =
= 
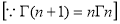
= 

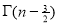
= 


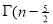 ) .......................
) .......................
= 

= 


Question-15: Evaluate 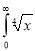
 dx.
dx.
Solution : Let 

 dx
dx
X | 0 |  |
t | 0 |  |
Put  or
or 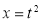 ;dx =2t dt .
;dx =2t dt .
 dt
dt
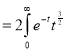 dt
dt
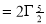
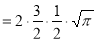
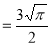
Question-16: Evaluate 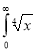
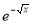 dx.
dx.
Solution : Let 
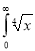
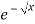 dx
dx
X | 0 |  |
t | 0 |  |
Put  or
or  ;dx =2t dt .
;dx =2t dt .
 dt
dt
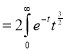 dt
dt
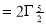
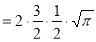
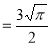
Question-17: Evaluate I = 
Solution:
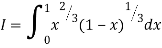
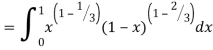
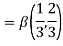
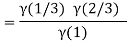
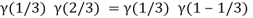
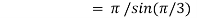
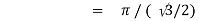
= 2 π/3
Question-18: Prove that
Solution : Let
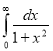
Put or
or  ,
, 
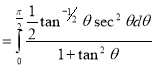
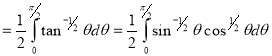





Question-19: Evaluate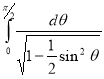
Solution :Let
Put  or
or  ,
,
 ,
,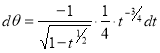
When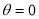 ,
, ;
;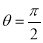 ,
,
 | o |  |
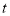 | 1 | 0 |
Also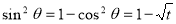


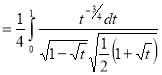

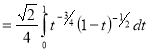
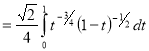

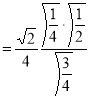
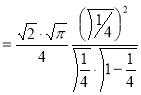



Question-20: Show that
Solution :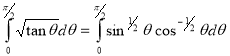
=
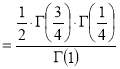
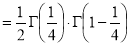

 (
(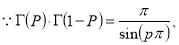 0<p<1)
0<p<1)
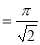
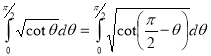
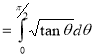
 (by above result)
(by above result) 

Question Bank(unit-4)
Question-1: Verify Rolle’s theorem for the function f(x) = x(x+3)
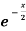
Sol. First we will differentiate the given function with respect to x, we get
f’(x) = (x²+3x)  + (2x + 3)
+ (2x + 3)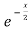
= 
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.
Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).
Here f(x) satisfies all the conditions of Rolle’s theorem,
Then,
f’(x) = 0 , which gives
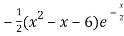 = 0
= 0
We get,
X = 3 and x = -2
Here we can see that clearly -3<-2<0 , therefore there exists -2 ∈ (-3,0) such that
f’(-2) = 0
That means the Rolle’s theorem is true for the given function.
Question-2: Verify Rolle’s theorem for the given functions below-
1. f(x) = x³ - 6x²+11x-6 in the interval [1,3]
2. f(x) = x²-4x+8 in the interval [1,3]
Sol. (1)
As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = f(3) = 0
Now we find f’(x) = 0
3x² - 12x +11 = 0
We get, x = 2+  and 2 -
and 2 - 
Hence both of them lie in (1,3).
Hence the theorem holds good for the given function in interval [1,3]
(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]
Also, f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5
Hence f(1) = f(3)
Now the first derivative of the function,
f’(x) = 0
2x – 4 = 0 , gives
X = 2
We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.
This means that the Rolle’s theorem holds good for the given function and given interval.
Question-3: Verify the Rolle’s theorem for sin x in the interval [ ]
]
Sol. Suppose f(x) = sin x
We know that sin x is continuous for all x.
Now , f’(x) = cos x exists for all x in (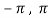 ) and
) and
f( 0
0
f( 0
0
Thus f(x) satisfies all the conditions of Rolle’s theorem.
Now,
f’(x) = 0 that gives , cos x = 0
x = 
Here we notice that both intervals lie in ( .
.
There exists, c = 
So that, f’(c) = 0
The Rolle’s theorem has been verified.
Question-4: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) = 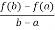 =
=  =
=  = 3
= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2 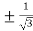
Here we see that the value of c lies between 0 and 4
Therefore the given function is verified.
Question-5: Verify Lagrange’s mean value theorem for f(x) = log x in [1,e].
Sol. We already know that the function which is log x is continuous for all x>0.
So that this is the continuous function In [1,e]
Now,
f’(x) = 1/x
Which is exists for all x in (1,e)
So that f(x) is differentiable in (1,e).
By Lagrange’s mean value theorem, we get
f’(c) =  , let x = c,
, let x = c,
then ,
f’(c) = 
We get,
c = e-1
e-1 will always lies between 1 and e .
Hence the function is verified by Lagrange’s mean value theorem
Question-6: Verify Cauchy’s mean value theorem for the function f(x) = sin x and g(x) = cos x in [ 0 , π/2]
Sol. It is given that ,
f(x) = sin x and g(x) = cos x
now ,
f’(x) = cos x and g’(x) = - sin x
We know that both the functions are continuous in [ 0 , π/2] and differentiable in ( 0 , π/2 )
Also , g’(x) = -sin x ≠ 0 for all x ϵ( 0 , π/2 )
By Cauchy’s mean value theorem , we get

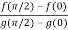 for some c: 0< c <
for some c: 0< c < 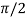
That means
 which gives,
which gives,
Cot c = 1
C = 
Now we see that  lies between 0 and
lies between 0 and 
Question-7: Find the Taylor’s series for the function f(x) = 3x² - 6x + 5 in ascending powers of x-3.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) + 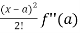 + ………
+ ……… . ………….(1)
. ………….(1)
Here ,
f(x) = 3x² - 6x + 5 and a = 3. So that f(a) = 14
Now , we will find out the derivatives ,
f’(x) = 6x – 6 and f’(3) = 12
f’’(x) = 6 and f’’(3) = 6
f’’’(x) = 0 and f’’’(x) = 14
Put these values in Taylor’s theorem, we get
3x² - 6x + 5 = 14 + 12(x-3) + 6  +…………. Ans.
+…………. Ans.
Question-8: Determine the area under the curves y = 2x² + 10 and y = 4x + 16.
Sol. Here we will find out the intersection, which are the boundaries of the curve,
2x² + 10 = 4x + 16
2x² - 4x – 6 = 0
2 (x + 1) ( x – 3 ) = 0
We get, x = -1 and x = 3,
We know that, Area under the curve,
A = 

Question-9: A force of 1200 N compresses a spring from its natural length of 18 cm to a length of 16 cm. How much work is done in compressing it from 16 cm to 14 cm?
Sol. Here,
F = kx
So that,
1200 = 2k
K = 600 N/cm
In that case,
F = 600x
We know that,
W = 
W = 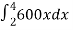 , which gives
, which gives
W = 3600 N.cm
Question-10: using slicing method, find out the volume of solid of revolution bounded by f(x) = x² - 4x +5 , x = 1 and x = 4, rotated about the x-axis.
Sol. Intervals are given. [ 1 , 4]
Here the solid is formed by revolving the region about x-axis , the cross – sections are circle .
Area of the cross section is , then is the area of circle, here radius of the circle is given by f(x).
We know that,
Area of the circle= π r²
= π [f(x)]²
= π[x² - 4x +5]²
Volume will be,
V = 
= 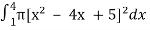
=  which gives,
which gives,
=  π
π
So the volume is  π
π
Question-11 Find the volume of the solid of revolution generated by rotating the region between the graph of f(x) = √x over the interval [1,4] around x-axis.
Sol. The graph of the function will look like as follow,

On rotation it will make circle ( cross-section)
We know that,
V = 
=  =
=  , which gives
, which gives
= 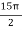
The volume is 
Question-12: suppose a wire hanging on two poles follows the curve,
f(x) = a cosh(x/a)
Find the length of the wire.
Sol. We will find the first derivative of f(x),
f’(x) = sinh(x/a)
The curve of f(x) will look like,

Hence the curve os symmetric, we will measure the length of one side first,
The limits on one side will be, 0 to b
We know that
Length of Arc = 
Put f’(x) = sinh(x/a), we get
Length of Arc = 
Use the identity,

= 
= 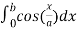
We get on solving,
a sinh(b/a)
On both sides, the length of the curve will be,
2 a sinh(b/a)
Question-13: find the surface of the surface generated by revolving the graph f(x) = 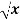 over the interval [1,4] around x-axis.
over the interval [1,4] around x-axis.
Sol. The graph of the function will look like
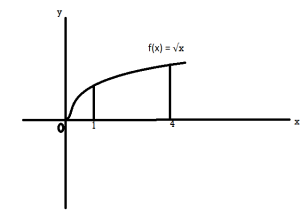
f(x) = 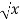 then f’(x) = 1/2 (
then f’(x) = 1/2 (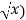
(f’(x))² = 1/4x
Then,
S = 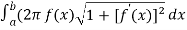
S = 
S =  ,
,
Let u =  , then du = dx, when x = 1 , u = 5/4 and when x = 4 , u = 17/4,
, then du = dx, when x = 1 , u = 5/4 and when x = 4 , u = 17/4,
This will give,
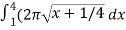 =
= 
On solving the integral we get,
 = 30.84 (approx.)
= 30.84 (approx.)
Question-14: Show that 

Solution :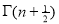 =
= 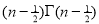

= 

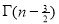
= 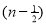
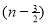

 ) .......................
) .......................
= 

= 


Question-15: Evaluate 
 dx.
dx.
Solution : Let 
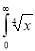
 dx
dx
X | 0 | 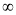 |
t | 0 | 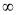 |
Put  or
or 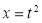 ;dx =2t dt .
;dx =2t dt .
 dt
dt
 dt
dt
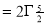
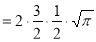
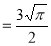
Question-16: Evaluate 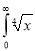
 dx.
dx.
Solution : Let 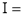

 dx
dx
X | 0 |  |
t | 0 |  |
Put  or
or  ;dx =2t dt .
;dx =2t dt .
 dt
dt
 dt
dt
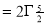
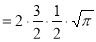
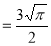
Question-17: Evaluate I = 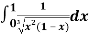
Solution:
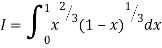
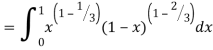
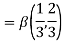
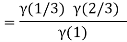
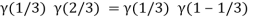
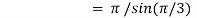
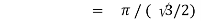
= 2 π/3
Question-18: Prove that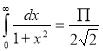
Solution : Let

Put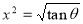 or
or  ,
, 
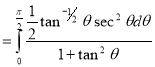
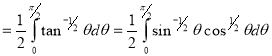





Question-19: Evaluate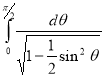
Solution :Let
Put  or
or 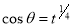 ,
,
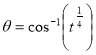 ,
,
When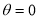 ,
, ;
; ,
,
 | o | 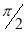 |
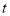 | 1 | 0 |
Also
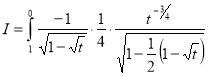



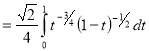
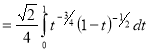






Question-20: Show that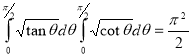
Solution :
=
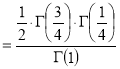


 (
( 0<p<1)
0<p<1)
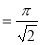
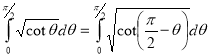
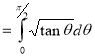
 (by above result)
(by above result)