UNIT 5
ELECTROMAGNETISM AND MAGNETIC PROPERTIES OF MATERIALS
1 Question: Discuss continuity equation for current density?
Solution:
Consider a closed surface S enclosing a Volume V through which currents are flowing. Let I be the current passing through the surface at any time t. Consider a small area 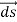 of the closed surface. The outward current flowing through
of the closed surface. The outward current flowing through  at a time t is
at a time t is

DI = 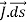 …………..(1)
…………..(1)
The total current flowing out through the closed surface S at time t is
I =  …………..(2)
…………..(2)
Suppose is ρ the Volume Charge density of charges inside the surface S. Then the total charge inside the Volume V is
q =  …………..(3)
…………..(3)
Since the current is flowing outward is it mean that charge within the enclosed surface is decreasing with time. The time rate of decrease of charge is
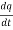 = -
= -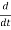
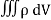 …………..(4)
…………..(4)
The negative sign shows that the charge inside the surface S is decreasing with time. The above equation can be written as
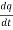 = -
= -  …………..(5)
…………..(5)
Since the charge is conserved, the current flowing outward through the closed surface must be equal to the rate of decrease of charge. Thus
I = 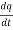
Using equation (2) and (5), it becomes
 = -
= - 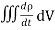 …………..(6)
…………..(6)
According to divergence theorem
 =
= 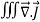 dV
dV
Using this result in equation (6) we obtain
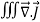 dV = -
dV = - 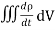
This equation holds good for arbitrary volumes. Therefore the integrands must be equal. Hence

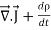 =0 …………..(7)
=0 …………..(7)
This equation is called equation of continuity. It is the mathematical statement of law of conservation of charge.
SPECIAL CASE
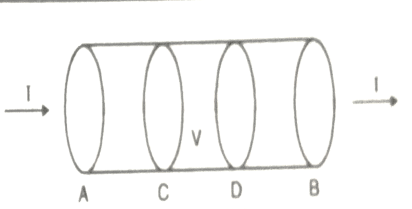
Consider a conductor AB through which a steady current I is flowing. The current I is said to be steady if charge is flowing per unit time through any two any sections C and D is the same. This means that the total amount of charge entering the volume V through C is equal to the charge leaving the volume V through D. Thus there is no change in the volume charge density in the volume V with time i.e.
 =0
=0
We may define steady current as that current in which the charge density is independent of time.
Using equation (7) we obtain
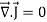
This is known as the equation of continuity for steady currents.
2 Question: If the electric field strength, E of an electromagnetic wave in free space is given by
E = 2 cos (t -  ) ay V/m,
) ay V/m,
Find the magnetic field, H
Solution:
We have
B/t =-x E
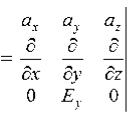
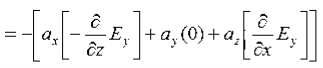
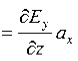

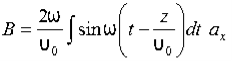

Thus
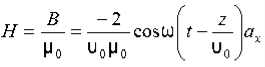
Also
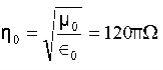
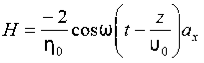
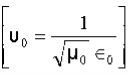
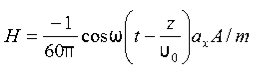
3. Question: For a long solenoid the magnetic field strength within the solenoid is given by the equation B=5.0t T, where t is time in seconds. If the induced electric field outside the solenoid is 11 V/m a distance 2.0 m from the axis of the solenoid, find the radius of the solenoid.
Solution:
Given
When there is a changing magnetic field through a coil, it causes an induced emf in the coil, which is based on the Faraday's law of electromagnetic induction. Further, the induced emf is related to the induced electric field along the circumference of the coil.
Magnetic field inside the solenoid, B =5.0×t T
Induced electric field at radial distance (from the axis of solenoid) r = 2.0 m is E =11 V/m
Radius (R) of solenoid =?
The induced electric field at the radial distance r from the axis of the solenoid is expressed as:
E×(2πr) =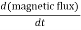
E×(2πr) =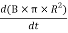
E×(2×r) =R2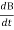
E×(2×r) = R2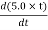
11×(2×2) =R2×5
R= 2.966  3.0 m
3.0 m
4. Question: A coil has 1000 turns and 500 cm2 as it's area. The plane of the coil is placed at right angles to a magnetic induction field of 2×10−5 Wb/m2. The coil is rotated through 1800 in 0.2 seconds. What is the average emf induced in the coil (in milli volts)?
Solution:
The induced emf will be given by
emf=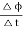
=
=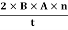
=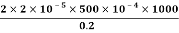
=10×10−3V=10 mV
5 Question: In a uniform magnetic field of induction B, a wire in the form of semicircle of radius r rotates about the diameter of the circle with angular velocity ω. If the total resistance of the circuit is R, then find the mean power generated per period of rotation.

Figure
Solution:

6. Question: Discuss Faraday’s law of electromagnetic induction? Solution:
Faraday’s law of electromagnetic induction (referred to as Faraday’s law) is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (EMF). This phenomenon is known as electromagnetic induction.
Faraday’s law states that a current will be induced in a conductor which is exposed to a changing magnetic field. Lenz’s law of electromagnetic induction states that the direction of this induced current will be such that the magnetic field created by the induced current opposes the initial changing magnetic field which produced it. The direction of this current flow can be determined using Fleming’s right-hand rule.
Let us understand Faraday’s law by faraday‘s experiment.
FARADAY’S EXPERIMENT
In this experiment, Faraday takes a magnet and a coil and connects a galvanometer across the coil. At starting, the magnet is at rest, so there is no deflection in the galvanometer i.e. the needle of the galvanometer is at the center or zero position. When the magnet is moved towards the coil, the needle of the galvanometer deflects in one direction.
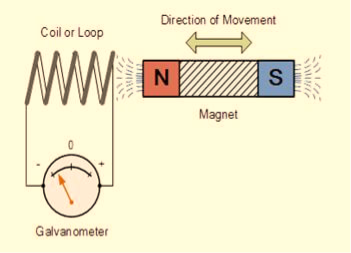
Figure 9
When the magnet is held stationary at that position, the needle of galvanometer returns to zero position. Now when the magnet moves away from the coil, there is some deflection in the needle but opposite direction, and again when the magnet becomes stationary, at that point respect to the coil, the needle of the galvanometer returns to the zero position.
Similarly, if the magnet is held stationary and the coil moves away, and towards the magnet, the galvanometer similarly shows deflection. It is also seen that the faster the change in the magnetic field, the greater will be the induced EMF or voltage in the coil.
Let us take a look at the following table. This table is showing the observation of faraday’s experiment.
Position of magnet | Deflection in galvanometer |
Magnet at rest | No deflection in the galvanometer |
Magnet moves towards the coil | Deflection in galvanometer in one direction |
Magnet is held stationary at same position (near the coil) | No deflection in the galvanometer |
Magnet moves away from the coil | Deflection in galvanometer but in the opposite direction |
Magnet is held stationary at the same position (away from the coil) | No deflection in the galvanometer |
CONCLUSION
From this experiment, Faraday concluded that whenever there is relative motion between a conductor and a magnetic field, the flux linkage with a coil changes and this change in flux induces a voltage across a coil.
Michael Faraday formulated two laws on the basis of the above experiments. These laws are called Faraday’s laws of electromagnetic induction.
FARADAY’S FIRST LAW
Any change in the magnetic field of a coil of wire will cause an emf to be induced in the coil. This emf induced is called induced emf and if the conductor circuit is closed, the current will also circulate through the circuit and this current is called induced current.
Method to change the magnetic field:
- By moving a magnet towards or away from the coil
- By moving the coil into or out of the magnetic field
- By changing the area of a coil placed in the magnetic field
- By rotating the coil relative to the magnet
FARADAY’S SECOND LAW
It states that the magnitude of emf induced in the coil is equal to the rate of change of flux that linkages with the coil. The flux linkage of the coil is the product of the number of turns in the coil and flux associated with the coil.
According to Faraday’s law of electromagnetic induction, the rate of change of flux linkage is equal to induced emf.
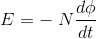 ………..(9)
………..(9)
Considering Lenz’s Law
Where:
- Flux Φ in Wb = B.A
- B = magnetic field strength
- A = area of the coil
FACTORS ON WHICH INDUCED EMF DEPEND
- By increasing the number of turns in the coil i.e. N, from the formulae derived above it is easily seen that if the number of turns in a coil is increased, the induced emf also gets increased.
- By increasing magnetic field strength i.e. B surrounding the coil- Mathematically, if magnetic field increases, flux increases and if flux increases emf induced will also get increased. Theoretically, if the coil is passed through a stronger magnetic field, there will be more lines of force for the coil to cut and hence there will be more emf induced.
- By increasing the speed of the relative motion between the coil and the magnet – If the relative speed between the coil and magnet is increased from its previous value, the coil will cut the lines of flux at a faster rate, so more induced emf would be produced.
7. Question: Give Physical Significance of Maxwell’s equation?
Solution:
Physical significance of Maxwell’s Ist equation
∇·E = ρ/ε0
According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.
Physical significance of Maxwell’s 2nd equation
∇·B = 0
It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.
Physical significance of Maxwell’s 3rd equation
∇×E = −∂B/∂t
It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.
Physical significance of Maxwell’s 4th equation
∇×H = J + ∂D/∂t
This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current density and displacement current density.
8 Question: Discuss Maxwell’s equations?
Solution:
Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.
Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects.
Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.
These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.
From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization.
We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed.
Maxwell’s first equation (Gauss' Law for Electric Fields)
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
∇·E = ρ/ε0
0r
∇·D = ρ
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
Maxwell’s second equation (Faraday's Law)
Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.
Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.
∇×E = −∂B/∂t(2)
Maxwell’s third equation (Ampere's Law)
Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced.
This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon.
The modified form of Ampere's Law s given by Maxwell’s third equation
∇×H = J + ∂D/∂t
Maxwell’s four equation (Gauss' Magnetism law)
We know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero.
Why? Why isn't the divergence of B equal to the magnetic charge density?
Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero:
∇·B = 0
Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.
Maxwell’s four equations are given by
∇·E = ρ/ε0(1)
∇×E = −∂B/∂t(2)
∇×H = J + ∂D/∂t(3)
∇·B = 0(4)
These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,
∇=(∂/∂x, ∂/∂y, ∂/∂z)
E is the electric vector
B is the magnetic induction
ρ is the electric charge density
j is the electric current density
ε0 is the permittivity of free space
c is the speed of light.
In addition to Maxwell equations, the following identities are useful:
J = σE(5)
D = εE(6)
B = μH(7)
Here,
D is the electric displacement
H is the magnetic vector
σ is the specific conductivity
ε is the dielectric constant (or permittivity)
μ is the magnetic permeability
9. Question: Define Gauss’s law? What is the value of Gauss’s law in free space?
Solution:
The law was published posthumously in 1867 as part of a collection of work by the famous German mathematician Carl Friedrich Gauss.
Gauss’s law for the electric field describes the static electric field generated by a distribution of electric charges.
It states that the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface.
Let’s calculate the electric flux through a spherical surface around a positive point charge q, since we already know the electric field in such a situation. Recall that when we place the point charge at the origin of a coordinate system, the electric field at a point P that is at a distance r
From the charge at the origin is given by
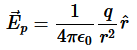
 is the radial vector from the charge at the origin to the point P. We can use this electric field to find the flux through the spherical surface of radius r, as shown in Figure 2
is the radial vector from the charge at the origin to the point P. We can use this electric field to find the flux through the spherical surface of radius r, as shown in Figure 2
.
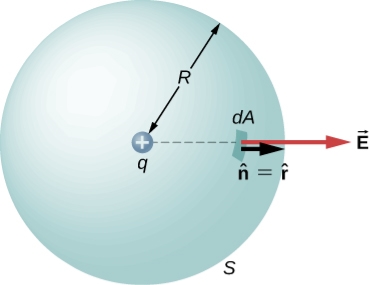
Figure 1: A closed spherical surface surrounding a point charge q.
Then we apply Φ=∫S  ⋅
⋅ dA
dA
To this system and substitute known values. On the sphere,  and r=R
and r=R
So for an infinitesimal area dA,
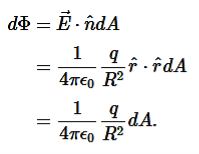
We now find the net flux by integrating this flux over the surface of the sphere
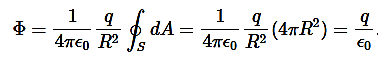
Where the total surface area of the spherical surface is 4πR2. This gives the flux through the closed spherical surface at radius r as
Φ=q/ϵ0
A remarkable fact about this equation is that the flux is independent of the size of the spherical surface. This can be directly attributed to the fact that the electric field of a point charge decreases as 1/r2 with distance, which just cancels the r2 rate of increase of the surface area.
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
∇·E = ρ/ε0
0r
∇·D = ρ
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
In integral form
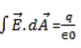
in differential form
∇·E = ρ/ε0
But in free space charge ρ is zero so ∇·E =0
10 Question: Derive Claussius -Mosotti equation?
Solution:
In dielectric solids, the atoms or molecules experience not only the external applied electric field but also the electric field produced by the dipoles. The resultant electric field acting on the atoms or molecules of dielectric substance is called the local field or an internal field.
To find an expression for local electric field on a dielectric molecule or an atom, we consider a dielectric material in the electric field of intensity E, between the capacitor plates so that the material is uniformly polarized, as a result opposite type of charges are induced on the surface of the dielectric near the capacitor plates. The local field is calculated by using the method suggested by Lorentz.
According to this method,
Internal field or Local field in solids
Consider a dielectric material and is subjected to external field of intensity E1. The charges are induced on the dielectric plate and the induced electric field intensity is taken as E2. Let E3 be the field at the center of the material. E4 be the induced field due to the charges on the spherical cavity. The total internal field of the material is
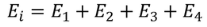 ………..(1)
………..(1)
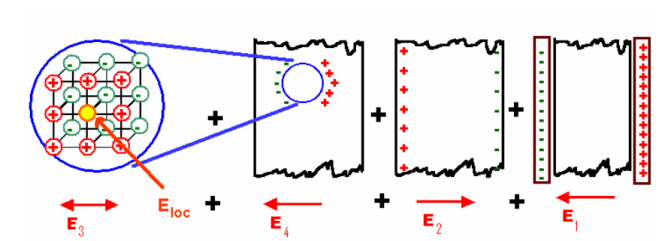
Now consider the Electric field intensity applied E1
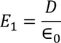 ………..(2)
………..(2)
We know
 ………..(3)
………..(3)
Substituting the Electric flux density D in E1, we get
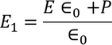 ………..(4)
………..(4)
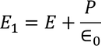 ………..(5)
………..(5)
E2 is the Electric field intensity due to induced or polarized charges
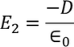 ………..(6)
………..(6)
Here the charge is induced due to the induced field so the electric flux density D changes to the electric polarization P
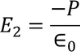 ………..(7)
………..(7)
Since we have considered that the specimen is non-polar dielectric material, at the center of the specimen the dipole moment is zero and hence the electric field intensity at the center is zero due to symmetric structure.
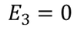 ………..(8)
………..(8)
Now consider a circle from the center of the dielectric material. Calculation of the electric field intensity E4 on the surface of spherical cavity.
As we know the polarization P is the induced charge per unit area
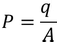 ………..(9)
………..(9)
Here the polarization changes to its component so we will take the component which is contributing.
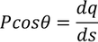
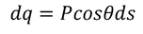 ………..(10)
………..(10)
Now this equation can be solved by finding out the values of the charge dq in the surface are dA. We know the Electric field intensity E
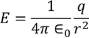 ………..(11)
………..(11)
Multiplying with the cosine angle on both the sides we get
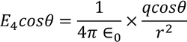 ………..(12)
………..(12)
Now by applying all the present condition for the above equation we
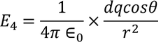 ………..(13)
………..(13)
Now substituting the charge dq in the above equation we get
 ………..(14)
………..(14)

If dA is the surface area of the sphere of radius r lying between θ and θ+dθ is the direction with reference to the direction of the applied force, then
DA= 2π(PQ)(QR)
But
Sinθ= PQ/r,
PQ = rsinθ ………..(15)
And
dθ=QR/r,
QR=r dθ………..(16)

Hence dA= 2πrsinθrdθ= 2πr2sinθdθ………..(17)
Now substituting all the values in the electric field intensity on the spherical cavity E4 we get,
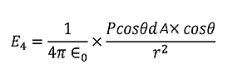 ………..(18)
………..(18)
Substituting (17) in (18), we get
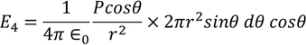
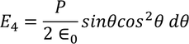 ………..(19)
………..(19)
Integrating with in the limits 0 to π
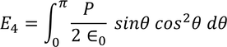
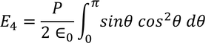 ………..(20)
………..(20)
On solving the integration we get,

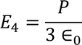 ………..(21)
………..(21)
So the total electric field
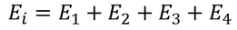
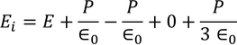 ………..(22)
………..(22)
Hence the Internal field obtained is
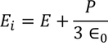 ………..(23)
………..(23)
Claussius -Mosotti Equation
It gives the relation between the dielectric constant and the ionic polarizability of atoms in dielectric material. If there are N number of atoms, the dipole moment per unit volume which is called Polarization is given by,
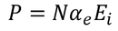 ………..(24)
………..(24)
We know internal field
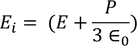 ………..(25)
………..(25)
From above equations
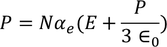
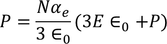
 ………..(26)
………..(26)
We know polarization from the relation between polarization and dielectric constant
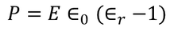 ………..(27)
………..(27)
From the above two equations we get,
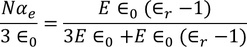
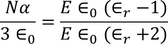
 ………..(28)
………..(28)
11 Question: Write a note on Ferroelectrics?
Solution:
Ferroelectrics
Ferroelectricity was first discovered in 1921 in a complex compound called Rochelle salt (Sodium potassium tartrate tetrahydrate). At that time it was the only material possessing the extraordinary property of reversible polarization. Later around 1935 ferroelectricity was observed in potassium dihydrogen phosphate (KH2PO4). The most popular and classical ferroelectric material BaTiO3 was discovered during World War II in 1941. BaTiO3 originally looked as a potential material for capacitors because of its high dielectric constant.
The high dielectric constant originates from the ferroelectric nature of BaTiO3. The physical quantity corresponding to the stored electric energy per unit area is called electric displacement D; it is related to the electric field E by the following simple expression
D= ε0E +P = εε0E
Where ε and ε0 are the material’s relative permittivity and permittivity of the vacuum respectively and P is the dielectric polarization, respectively.
When the centre of the positive and negative charges in the crystal structure do not coincide naturally (without application of any external field) such crystals are said to possess a spontaneous polarization. When, upon applying an electric field, such a spontaneous polarization can be reversed then the material is called ferroelectric.
Ferroelectrics are simply defined as the “class of materials which exhibits spontaneous electric polarization (in the absence of electric field) which reversible by applying an electric field”.
The term ferro in the ferroelectrics has nothing to do with the ferrous i.e., iron content in the materials, rather this term used to explain that this class of materials exhibit spontaneous electric polarization and electric hysteresis, analogous to the ferromagnetic properties of spontaneous magnetization and magnetic hysteresis.
The ferroelectric nature of a material depends crucially on the atomic structure. Other ferroelectric materials are Lead zirconate titanate (PZT), Lead lanthanum zirconate titanate (PLZT), Lithium niobate (LiNbO3), and relaxors like Lead magnesiumniobate (PMN).
12 Question: Write a note on Piezoelectric?
Solution:
Piezoelectric
All ferroelectric materials are piezoelectric (but the reverse is not true). In Piezoelectric “Piezo” derived from the Greek word “piezein” and the meaning of piezein is squeeze or press. So its name itself explaining the effect.
Direct Piezoelectric Effect
The piezoelectric effect transforms kinetic or mechanical energy into electrical energy, due to crystal deformation. When the material is compressed or squeezed, this Mechanical stress applied to the material generates electricity.
Microphones, speakers, buzzers, pressure sensors, hydrophones, and many other sensing types of devices use direct piezoelectric effect.
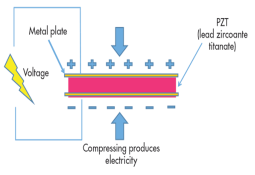
The above figure shows the direct piezoelectric effect
Figure 29: Direct Piezoelectric Effect
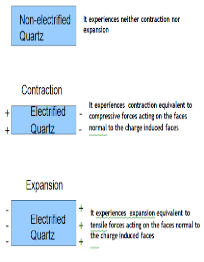
Inverse Piezoelectric Effect
We can reverse the same effect. Inverse piezoelectric effect – when an electric field is applied to a crystal it aligns all dipoles present in the material in order. This realignment results in deformation of crystal i.e. converting electrical energy into kinetic or mechanical energy. The reversal of the piezoelectric effect is called the inverse piezoelectric effect.
Using the inverse piezoelectric effect we can develop devices that produce acoustic sound waves. Even medical ultrasound and sonar transducers use the inverse piezoelectric effect.

The above figure shows the inverse piezoelectric effect
Figure 30: The Inverse Piezoelectric Effect
The basic equations describing the direct and converse piezoelectric effects can be expressed in terms of electric and elastic properties as follows
D = dE + εσE
S = sEσ + dE
Where D is the dielectric displacement, σ the stress, E the electric field, S the strain, d the piezoelectric coefficient, s the material compliance constant (inverse of the elastic constant) and ε is the material’s dielectric constant (permittivity). The superscript in the equations indicates that the quantity is held constant. In the case of εσ stress is held constant which implies that the piezoelectric element is mechanically unconstrained and in the case of sE, the electric field is held constant which implies electrodes on the elements are mutually shortened.
The direct and converse piezoelectric effects can also be conveniently expressed in terms of following tensor notations:
Pi = dijkσjk
Xij = dkijEk
In case of the direct piezoelectric effect Pi is the polarization generated along the i-axis, which is proportional to the applied stress σjk through the piezoelectric coefficients dijk. For the converse piezoelectric effect Xij is the strain generated in a particular orientation of the crystal when an electric field Ek is applied along a certain k-axis.
Examples of Piezoelectric Materials
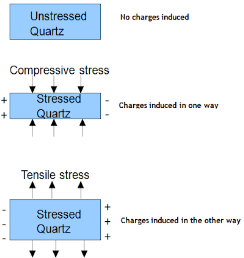
All piezoelectric materials are non-conductive for the piezoelectric effect to occur and work. Quartz is natural and first Piezoelectric Material whereas Lead Zirconate Titanate, Barium Titanate, and Lithium Niobate are man-made Piezoelectric Materials.
Q.13 Define Magnetic susceptibility (χ)
Solution:
If H is the applied magnetizing field intensity and M is the amount of magnetization of the material,
Then χ = 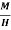
χ = 0 in vacuum
χ = +ve for paramagnetic and Ferro magnetic materials
χ = -ve for diamagnetic materials
Units: It has no units.
Q.14 How can we Classify Magnetic Materials?
Solution:
Magnetic materials are classified as follows:
- Diamagnetic
- Paramagnetic
- Ferromagnetic
- Anti-Ferro magnetic
- Ferric magnetic or ferrites
Diamagnetic
The orbital motion of electrons around the nucleus produces a magnetic field perpendicular to the plane of the orbit. Thus each electron orbit has a finite orbital magnetic dipole moment. Since the orbital planes are oriented randomly, the vector sum of magnetic moments is zero and there is no resultant magnetic moment for each atom.
In the presence of an external magnetic field, some electrons are speeded up and some are slowed down. The electrons whose moments were anti-parallel are speeded up according to Lenz’s law and this produces an induced magnetic moment in a direction opposite to the field. The induced moment disappears as soon as the external field is removed.
When placed in a non-uniform magnetic field, the interaction between the induced magnetic moment and the external field creates a force that tends to move the material from the stronger part to the weaker part of the external field. It means that diamagnetic material is repelled by the field.
This action is called diamagnetic action and such materials are known as diamagnetic materials. Examples: Bismuth, Copper, and Water, etc.
The properties of diamagnetic materials are
- Magnetic susceptibility is negative.
- Relative permeability is slightly less than unity.
- The magnetic field lines are repelled or expelled by diamagnetic materials when placed in a magnetic field.
- Susceptibility is nearly temperature independent.
- Examples: Cu, Au, Zn, H20, Bi, etc. organic materials
Paramagnetic materials
In some magnetic materials, each atom or molecule has a net magnetic dipole moment which is the vector sum of orbital and spin magnetic moments of electrons. Due to the random orientation of these magnetic moments, the net magnetic moment of the materials is zero.
In the presence of an external magnetic field, the torque acting on the atomic dipoles will align them in the field direction. As a result, there is a net magnetic dipole moment induced in the direction of the applied field. The induced dipole moment is present as long as the external field exists.
The properties of paramagnetic materials are:
- Magnetic susceptibility is positive and small.
- Relative permeability is greater than unity.
- The magnetic field lines are attracted to the paramagnetic materials when placed in a magnetic field.
- Susceptibility is inversely proportional to temperature.
Ferromagnetic materials
An atom or a molecule in a ferromagnetic material possesses a net magnetic dipole moment as in a paramagnetic material. A ferromagnetic material is made up of smaller regions, called ferromagnetic domain. Within each domain, the magnetic moments are spontaneously aligned in a direction. This alignment is caused by strong interaction arising from electron spin which depends on the inter-atomic distance. Each domain has net magnetization in a direction. However, the direction of magnetisation varies from domain to domain and thus net magnetisation of the specimen is zero.
In the presence of an external magnetic field, two processes take place
1. The domains having magnetic moments parallel to the field grow in size
2. The other domains (not parallel to the field) are rotated so that they are aligned with the field.
As a result of these mechanisms, there is a strong net magnetisation of the material in the direction of the applied field
When placed in a non-uniform magnetic field, the ferromagnetic materials will have a strong tendency to move from the weaker to the stronger part of the field. Materials that exhibit strong magnetism in the direction of the applied field are called ferromagnetic materials. Examples: Iron, Nickel, and Cobalt.
The properties of ferromagnetic materials are:
- Magnetic susceptibility is positive and large.
- Relative permeability is large.
- The magnetic field lines are strongly attracted to the ferromagnetic materials when placed in a magnetic field.
- Susceptibility is inversely proportional to temperature.
Antiferromagnetism
In the periodic table, the only element exhibiting antiferromagnetism at room temperature is chromium. Antiferromagnetic materials are very similar to ferromagnetic materials but the exchange interaction between neighboring atoms leads to the anti-parallel alignment of the atomic magnetic moments. Therefore, the magnetic field cancels out and the material appears to behave in the same way as a paramagnetic material. Like ferromagnetic materials, these materials become paramagnetic above a transition temperature, known as the Neel temperature, TN. (Cr: TN=37ºC).
The properties of antiferromagnetic materials are:
- They have permanent magnetic dipoles
- They do not possess a permanent magnetic dipole moment. Since in the absence of field, they have no spontaneous magnetization due to anti-parallel spin
- The relative permeability μr>1
- Susceptibility χ is small but negative
- 𝜒depends on temperature
Q.15 Discuss in brief the B-H curve?
Solution:
Magnetic Hysteresis
The lag or delay of a magnetic material known commonly as Magnetic Hysteresis relates to the magnetization properties of a material by which it first becomes magnetized and then de-magnetized.
The set of magnetization curves, M above represents an example of the relationship between B and H for soft-iron and steel cores but every type of core material will have its own set of magnetic hysteresis curves. You may notice that the flux density increases in proportion to the field strength until it reaches a certain value where it cannot increase any more becoming almost level and constant as the field strength continues to increase.
This is because there is a limit to the amount of flux density that can be generated by the core as all the domains in the iron are perfectly aligned. Any further increase will not affect the value of M, and the point on the graph where the flux density reaches its limit is called Magnetic Saturation also known as Saturation of the Core and in our simple example above the saturation point of the steel, the curve begins at about 3000 ampere-turns per metre.
As the magnetic field strength, ( H ) increases these molecular magnets become more and more aligned until they reach perfect alignment producing maximum flux density, and an increase in the magnetic field strength due to an increase in the electrical current flowing through the coil will have little or no effect.
Retentivity
Let’s assume that we have an electromagnetic coil with a high field strength due to the current flowing through it and that the ferromagnetic core material has reached its saturation point, maximum flux density. If we now open a switch and remove the magnetizing current flowing through the coil we would expect the magnetic field around the coil to disappear as the magnetic flux reduced to zero.
However, the magnetic flux does not completely disappear as the electromagnetic core material still retains some of its magnetism even when the current has stopped flowing in the coil. This ability for a coil to retain some of its magnetism within the core after the magnetization process has stopped is called Retentivity or remanence, while the amount of flux density remaining in the core is called Residual Magnetism, BR.
The reason for this that some of the tiny molecular magnets do not return to a completely random pattern and still point in the direction of the original magnetizing field giving them a sort of “memory”. Some ferromagnetic materials have a high retentivity (magnetically hard) making them excellent for producing permanent magnets.
While other ferromagnetic materials have low retentivity (magnetically soft) making them ideal for use in electromagnets, solenoids, or relays. One way to reduce this residual flux density to zero is by reversing the direction of the current flowing through the coil, thereby making the value of H, the magnetic field strength negative. This effect is called a Coercive Force, HC.
If this reverse current is increased further the flux density will also increase in the reverse direction until the ferromagnetic core reaches saturation again but in the reverse direction from before. Reducing the magnetizing current, i once again to zero will produce a similar amount of residual magnetism but in the reverse direction.
Then by constantly changing the direction of the magnetizing current through the coil from a positive direction to a negative direction, as would be the case in an AC supply, a Magnetic Hysteresis loop of the ferromagnetic core can be produced.
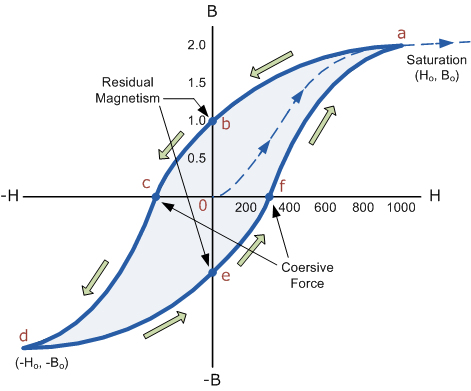
Figure 2
The B-H Curve or Magnetic Hysteresis loop above shows the behaviour of a ferromagnetic core graphically as the relationship between B and H is non-linear.
Starting with an unmagnetized core both B and H will be at zero, point 0 on the magnetization curve.
If the magnetization current, i is increased in a positive direction to some value the magnetic field strength H increases linearly with i and the flux density B will also increase as shown by the curve from point 0 to point a as it heads towards saturation.
Now if the magnetizing current in the coil is reduced to zero, the magnetic field circulating around the core also reduces to zero. However, the coils magnetic flux will not reach zero due to the residual magnetism present within the core and this is shown on the curve from point a to point b.
To reduce the flux density at point b to zero we need to reverse the current flowing through the coil. The magnetising force which must be applied to null the residual flux density is called a “Coercive Force”. This coercive force reverses the magnetic field re-arranging the molecular magnets until the core becomes unmagnetised at point c.
An increase in this reverse current causes the core to be magnetised in the opposite direction and increasing this magnetisation current further will cause the core to reach its saturation point but in the opposite direction, point d on the curve.
This point is symmetrical to point b. If the magnetising current is reduced again to zero the residual magnetism present in the core will be equal to the previous value but in reverse at point e.
Again reversing the magnetising current flowing through the coil this time into a positive direction will cause the magnetic flux to reach zero, point f on the curve and as before increasing the magnetisation current further in a positive direction will cause the core to reach saturation at point a.
Then the B-H curve follows the path of a-b-c-d-e-f-a as the magnetising current flowing through the coil alternates between a positive and negative value such as the cycle of an AC voltage. This path is called a B-H Curve or Magnetic Hysteresis Loop.
The effect of magnetic hysteresis shows that the magnetisation process of a ferromagnetic core and therefore the flux density depends on which part of the curve the ferromagnetic core is magnetised on as this depends upon the circuits past history giving the core a form of “memory”. Then ferromagnetic materials have memory because they remain magnetised after the external magnetic field has been removed.
However, soft ferromagnetic materials such as iron or silicon steel have very narrow magnetic hysteresis loops resulting in very small amounts of residual magnetism making them ideal for use in relays, solenoids, and transformers as they can be easily magnetised and demagnetised.
Since a coercive force must be applied to overcome this residual magnetism, work must be done in closing the hysteresis loop with the energy being used being dissipated as heat in the magnetic material. This heat is known as hysteresis loss, the amount of loss depends on the material’s value of coercive force.
By adding additives to the iron metal such as silicon, materials with a very small coercive force can be made that have a very narrow hysteresis loop. Materials with narrow hysteresis loops are easily magnetised and demagnetised and known as soft magnetic materials.
Q.16 Draw B-H Curve for Soft and Hard Materials?
Solution:
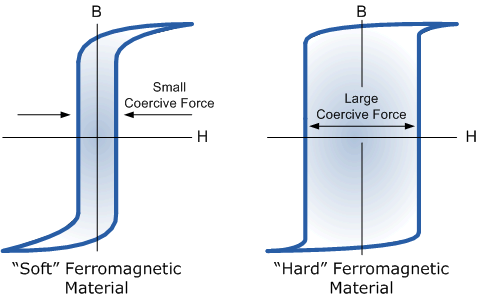
Figure 3
The shape of the hysteresis loop depends upon the nature of the iron or steel used and in the case of iron which is subjected to massive reversals of magnetism, for example, transformer cores, the B-H hysteresis loop must be as small as possible.
UNIT 5
ELECTROMAGNETISM AND MAGNETIC PROPERTIES OF MATERIALS
1 Question: Discuss continuity equation for current density?
Solution:
Consider a closed surface S enclosing a Volume V through which currents are flowing. Let I be the current passing through the surface at any time t. Consider a small area 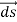 of the closed surface. The outward current flowing through
of the closed surface. The outward current flowing through 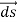 at a time t is
at a time t is

DI = 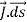 …………..(1)
…………..(1)
The total current flowing out through the closed surface S at time t is
I = 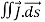 …………..(2)
…………..(2)
Suppose is ρ the Volume Charge density of charges inside the surface S. Then the total charge inside the Volume V is
q = 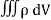 …………..(3)
…………..(3)
Since the current is flowing outward is it mean that charge within the enclosed surface is decreasing with time. The time rate of decrease of charge is
 = -
= -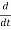
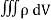 …………..(4)
…………..(4)
The negative sign shows that the charge inside the surface S is decreasing with time. The above equation can be written as
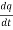 = -
= -  …………..(5)
…………..(5)
Since the charge is conserved, the current flowing outward through the closed surface must be equal to the rate of decrease of charge. Thus
I = 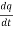
Using equation (2) and (5), it becomes
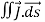 = -
= - 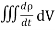 …………..(6)
…………..(6)
According to divergence theorem
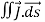 =
=  dV
dV
Using this result in equation (6) we obtain
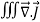 dV = -
dV = - 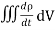
This equation holds good for arbitrary volumes. Therefore the integrands must be equal. Hence
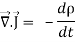
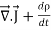 =0 …………..(7)
=0 …………..(7)
This equation is called equation of continuity. It is the mathematical statement of law of conservation of charge.
SPECIAL CASE
Consider a conductor AB through which a steady current I is flowing. The current I is said to be steady if charge is flowing per unit time through any two any sections C and D is the same. This means that the total amount of charge entering the volume V through C is equal to the charge leaving the volume V through D. Thus there is no change in the volume charge density in the volume V with time i.e.
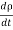 =0
=0

We may define steady current as that current in which the charge density is independent of time.
Using equation (7) we obtain
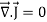
This is known as the equation of continuity for steady currents.
2 Question: If the electric field strength, E of an electromagnetic wave in free space is given by
E = 2 cos (t - 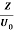 ) ay V/m,
) ay V/m,
Find the magnetic field, H
Solution:
We have
B/t =-x E
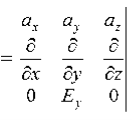


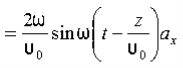
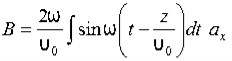
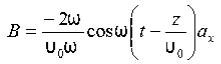
Thus
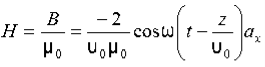
Also
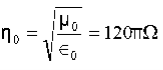

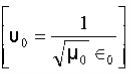

3. Question: For a long solenoid the magnetic field strength within the solenoid is given by the equation B=5.0t T, where t is time in seconds. If the induced electric field outside the solenoid is 11 V/m a distance 2.0 m from the axis of the solenoid, find the radius of the solenoid.
Solution:
Given
When there is a changing magnetic field through a coil, it causes an induced emf in the coil, which is based on the Faraday's law of electromagnetic induction. Further, the induced emf is related to the induced electric field along the circumference of the coil.
Magnetic field inside the solenoid, B =5.0×t T
Induced electric field at radial distance (from the axis of solenoid) r = 2.0 m is E =11 V/m
Radius (R) of solenoid =?
The induced electric field at the radial distance r from the axis of the solenoid is expressed as:
E×(2πr) =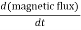
E×(2πr) =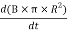
E×(2×r) =R2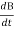
E×(2×r) = R2
11×(2×2) =R2×5
R= 2.966  3.0 m
3.0 m
4. Question: A coil has 1000 turns and 500 cm2 as it's area. The plane of the coil is placed at right angles to a magnetic induction field of 2×10−5 Wb/m2. The coil is rotated through 1800 in 0.2 seconds. What is the average emf induced in the coil (in milli volts)?
Solution:
The induced emf will be given by
emf=
=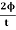
=
=
=10×10−3V=10 mV
5 Question: In a uniform magnetic field of induction B, a wire in the form of semicircle of radius r rotates about the diameter of the circle with angular velocity ω. If the total resistance of the circuit is R, then find the mean power generated per period of rotation.
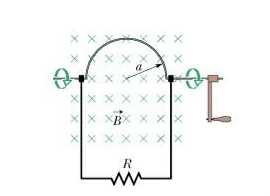
Figure
Solution:

6. Question: Discuss Faraday’s law of electromagnetic induction? Solution:
Faraday’s law of electromagnetic induction (referred to as Faraday’s law) is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (EMF). This phenomenon is known as electromagnetic induction.
Faraday’s law states that a current will be induced in a conductor which is exposed to a changing magnetic field. Lenz’s law of electromagnetic induction states that the direction of this induced current will be such that the magnetic field created by the induced current opposes the initial changing magnetic field which produced it. The direction of this current flow can be determined using Fleming’s right-hand rule.
Let us understand Faraday’s law by faraday‘s experiment.
FARADAY’S EXPERIMENT
In this experiment, Faraday takes a magnet and a coil and connects a galvanometer across the coil. At starting, the magnet is at rest, so there is no deflection in the galvanometer i.e. the needle of the galvanometer is at the center or zero position. When the magnet is moved towards the coil, the needle of the galvanometer deflects in one direction.
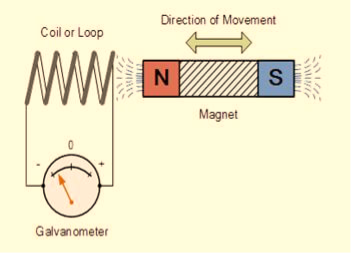
Figure 9
When the magnet is held stationary at that position, the needle of galvanometer returns to zero position. Now when the magnet moves away from the coil, there is some deflection in the needle but opposite direction, and again when the magnet becomes stationary, at that point respect to the coil, the needle of the galvanometer returns to the zero position.
Similarly, if the magnet is held stationary and the coil moves away, and towards the magnet, the galvanometer similarly shows deflection. It is also seen that the faster the change in the magnetic field, the greater will be the induced EMF or voltage in the coil.
Let us take a look at the following table. This table is showing the observation of faraday’s experiment.
Position of magnet | Deflection in galvanometer |
Magnet at rest | No deflection in the galvanometer |
Magnet moves towards the coil | Deflection in galvanometer in one direction |
Magnet is held stationary at same position (near the coil) | No deflection in the galvanometer |
Magnet moves away from the coil | Deflection in galvanometer but in the opposite direction |
Magnet is held stationary at the same position (away from the coil) | No deflection in the galvanometer |
CONCLUSION
From this experiment, Faraday concluded that whenever there is relative motion between a conductor and a magnetic field, the flux linkage with a coil changes and this change in flux induces a voltage across a coil.
Michael Faraday formulated two laws on the basis of the above experiments. These laws are called Faraday’s laws of electromagnetic induction.
FARADAY’S FIRST LAW
Any change in the magnetic field of a coil of wire will cause an emf to be induced in the coil. This emf induced is called induced emf and if the conductor circuit is closed, the current will also circulate through the circuit and this current is called induced current.
Method to change the magnetic field:
- By moving a magnet towards or away from the coil
- By moving the coil into or out of the magnetic field
- By changing the area of a coil placed in the magnetic field
- By rotating the coil relative to the magnet
FARADAY’S SECOND LAW
It states that the magnitude of emf induced in the coil is equal to the rate of change of flux that linkages with the coil. The flux linkage of the coil is the product of the number of turns in the coil and flux associated with the coil.
According to Faraday’s law of electromagnetic induction, the rate of change of flux linkage is equal to induced emf.
 ………..(9)
………..(9)
Considering Lenz’s Law
Where:
- Flux Φ in Wb = B.A
- B = magnetic field strength
- A = area of the coil
FACTORS ON WHICH INDUCED EMF DEPEND
- By increasing the number of turns in the coil i.e. N, from the formulae derived above it is easily seen that if the number of turns in a coil is increased, the induced emf also gets increased.
- By increasing magnetic field strength i.e. B surrounding the coil- Mathematically, if magnetic field increases, flux increases and if flux increases emf induced will also get increased. Theoretically, if the coil is passed through a stronger magnetic field, there will be more lines of force for the coil to cut and hence there will be more emf induced.
- By increasing the speed of the relative motion between the coil and the magnet – If the relative speed between the coil and magnet is increased from its previous value, the coil will cut the lines of flux at a faster rate, so more induced emf would be produced.
7. Question: Give Physical Significance of Maxwell’s equation?
Solution:
Physical significance of Maxwell’s Ist equation
∇·E = ρ/ε0
According to this total electric flux through any closed surface is 1/0 times the total charge enclosed by the closed surfaces, representing Gauss's law of electrostatics, As this does not depend on time, it is a steady state equation. Here for positive , divergence of electric field is positive and for negative divergence is negative. It indicates that is scalar quantity.
Physical significance of Maxwell’s 2nd equation
∇·B = 0
It represents Gauss law of magnetostatic as ∇·B = 0 resulting that isolated magnetic poles or magnetic monopoles cannot exist as they appear only in pairs and there is no source or sink for magnetic lines of forces. It is also independent of time i.e. steady state equation.
Physical significance of Maxwell’s 3rd equation
∇×E = −∂B/∂t
It shows that with time varying magnetic flux, electric field is produced in accordance with Faraday is law of electromagnetic induction. This is a time dependent equation.
Physical significance of Maxwell’s 4th equation
∇×H = J + ∂D/∂t
This is a time dependent equation which represents the modified differential form of Ampere's circuital law according to which magnetic field is produced due to combined effect of conduction current density and displacement current density.
8 Question: Discuss Maxwell’s equations?
Solution:
Maxwell equations are of fundamental importance since they describe the whole of classical electromagnetic phenomena.
Maxwell's Equations are a set of 4 complicated equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects.
Maxwell was one of the first to determine the speed of propagation of electromagnetic (EM) waves was the same as the speed of light - and hence to conclude that EM waves and visible light were really the same thing.
These equations are rules the universe uses to govern the behaviour of electric and magnetic fields. A flow of electric current will produce a magnetic field. If the current flow varies with time (as in any wave or periodic signal), the magnetic field will also give rise to an electric field. Maxwell's Equations shows that separated charge (positive and negative) gives rise to an electric field - and if this is varying in time as well will give rise to a propagating electric field, further giving rise to a propagating magnetic field.
From a classical perspective, light can be described as waves of electromagnetic radiation. As such, Maxwell equations are very useful to illustrate a number of the characteristics of light including polarization.
We are just to stating these equations without derivation. Since our goal is simply to apply them, the usual approach will be followed.
Maxwell’s first equation (Gauss' Law for Electric Fields)
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
∇·E = ρ/ε0
0r
∇·D = ρ
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
Maxwell’s second equation (Faraday's Law)
Faraday figured out that a changing Magnetic Flux within a circuit (or closed loop of wire) produced an induced EMF, or voltage within the circuit. Maxwell gives his second equation from this.
Faraday's Law tells us that a magnetic field that is changing in time will give rise to a circulating E-field. This means we have two ways of generating E-fields - from Electric Charges (or flowing electric charge, current) or from a magnetic field that is changing.
∇×E = −∂B/∂t(2)
Maxwell’s third equation (Ampere's Law)
Ampere's Law tells us that a flowing electric current gives rise to a magnetic field that circles the wire. In addition to this, it also says that an Electric Field that is changing in time gives rise to a magnetic field that encircles the E-field - this is the Displacement Current term that Maxwell himself introduced.
This means there are 2 ways to generate a solenoidal (circulating) H-field - a flowing electric current or a changing Electric Field. Both give rise to the same phenomenon.
The modified form of Ampere's Law s given by Maxwell’s third equation
∇×H = J + ∂D/∂t
Maxwell’s four equation (Gauss' Magnetism law)
We know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero.
Why? Why isn't the divergence of B equal to the magnetic charge density?
Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero:
∇·B = 0
Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attract like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and South Pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet.
Maxwell’s four equations are given by
∇·E = ρ/ε0(1)
∇×E = −∂B/∂t(2)
∇×H = J + ∂D/∂t(3)
∇·B = 0(4)
These equations illustrate the unique coexistence in nature of the electric field and the magnetic field. The first two equations give the value of the given flux through a closed surface, and the second two equations give the value of a line integral around a loop. In this notation,
∇=(∂/∂x, ∂/∂y, ∂/∂z)
E is the electric vector
B is the magnetic induction
ρ is the electric charge density
j is the electric current density
ε0 is the permittivity of free space
c is the speed of light.
In addition to Maxwell equations, the following identities are useful:
J = σE(5)
D = εE(6)
B = μH(7)
Here,
D is the electric displacement
H is the magnetic vector
σ is the specific conductivity
ε is the dielectric constant (or permittivity)
μ is the magnetic permeability
9. Question: Define Gauss’s law? What is the value of Gauss’s law in free space?
Solution:
The law was published posthumously in 1867 as part of a collection of work by the famous German mathematician Carl Friedrich Gauss.
Gauss’s law for the electric field describes the static electric field generated by a distribution of electric charges.
It states that the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface.
Let’s calculate the electric flux through a spherical surface around a positive point charge q, since we already know the electric field in such a situation. Recall that when we place the point charge at the origin of a coordinate system, the electric field at a point P that is at a distance r
From the charge at the origin is given by
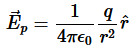
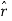 is the radial vector from the charge at the origin to the point P. We can use this electric field to find the flux through the spherical surface of radius r, as shown in Figure 2
is the radial vector from the charge at the origin to the point P. We can use this electric field to find the flux through the spherical surface of radius r, as shown in Figure 2
.
Figure 1: A closed spherical surface surrounding a point charge q.
Then we apply Φ=∫S  ⋅
⋅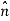 dA
dA
To this system and substitute known values. On the sphere,  and r=R
and r=R
So for an infinitesimal area dA,
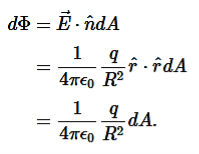
We now find the net flux by integrating this flux over the surface of the sphere
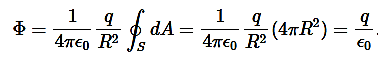
Where the total surface area of the spherical surface is 4πR2. This gives the flux through the closed spherical surface at radius r as
Φ=q/ϵ0
A remarkable fact about this equation is that the flux is independent of the size of the spherical surface. This can be directly attributed to the fact that the electric field of a point charge decreases as 1/r2 with distance, which just cancels the r2 rate of increase of the surface area.
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
∇·E = ρ/ε0
0r
∇·D = ρ
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
In integral form
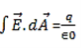
in differential form
∇·E = ρ/ε0
But in free space charge ρ is zero so ∇·E =0
10 Question: Derive Claussius -Mosotti equation?
Solution:
In dielectric solids, the atoms or molecules experience not only the external applied electric field but also the electric field produced by the dipoles. The resultant electric field acting on the atoms or molecules of dielectric substance is called the local field or an internal field.
To find an expression for local electric field on a dielectric molecule or an atom, we consider a dielectric material in the electric field of intensity E, between the capacitor plates so that the material is uniformly polarized, as a result opposite type of charges are induced on the surface of the dielectric near the capacitor plates. The local field is calculated by using the method suggested by Lorentz.
According to this method,
Internal field or Local field in solids
Consider a dielectric material and is subjected to external field of intensity E1. The charges are induced on the dielectric plate and the induced electric field intensity is taken as E2. Let E3 be the field at the center of the material. E4 be the induced field due to the charges on the spherical cavity. The total internal field of the material is
 ………..(1)
………..(1)
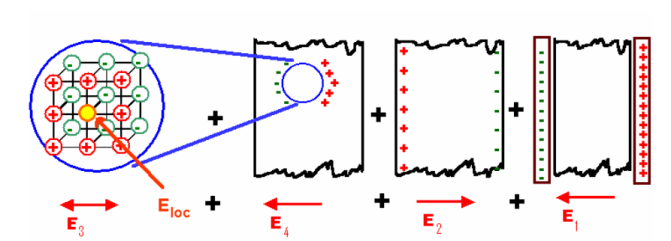
Now consider the Electric field intensity applied E1
 ………..(2)
………..(2)
We know
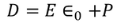 ………..(3)
………..(3)
Substituting the Electric flux density D in E1, we get
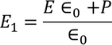 ………..(4)
………..(4)
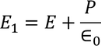 ………..(5)
………..(5)
E2 is the Electric field intensity due to induced or polarized charges
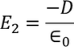 ………..(6)
………..(6)
Here the charge is induced due to the induced field so the electric flux density D changes to the electric polarization P
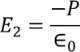 ………..(7)
………..(7)
Since we have considered that the specimen is non-polar dielectric material, at the center of the specimen the dipole moment is zero and hence the electric field intensity at the center is zero due to symmetric structure.
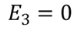 ………..(8)
………..(8)
Now consider a circle from the center of the dielectric material. Calculation of the electric field intensity E4 on the surface of spherical cavity.
As we know the polarization P is the induced charge per unit area
 ………..(9)
………..(9)
Here the polarization changes to its component so we will take the component which is contributing.
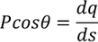
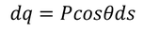 ………..(10)
………..(10)
Now this equation can be solved by finding out the values of the charge dq in the surface are dA. We know the Electric field intensity E
 ………..(11)
………..(11)
Multiplying with the cosine angle on both the sides we get
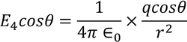 ………..(12)
………..(12)
Now by applying all the present condition for the above equation we
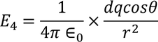 ………..(13)
………..(13)
Now substituting the charge dq in the above equation we get
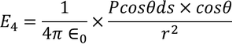 ………..(14)
………..(14)

If dA is the surface area of the sphere of radius r lying between θ and θ+dθ is the direction with reference to the direction of the applied force, then
DA= 2π(PQ)(QR)
But
Sinθ= PQ/r,
PQ = rsinθ ………..(15)
And
dθ=QR/r,
QR=r dθ………..(16)

Hence dA= 2πrsinθrdθ= 2πr2sinθdθ………..(17)
Now substituting all the values in the electric field intensity on the spherical cavity E4 we get,
 ………..(18)
………..(18)
Substituting (17) in (18), we get
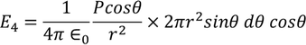
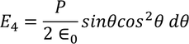 ………..(19)
………..(19)
Integrating with in the limits 0 to π

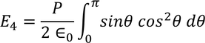 ………..(20)
………..(20)
On solving the integration we get,
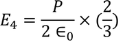
 ………..(21)
………..(21)
So the total electric field
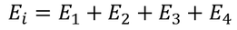
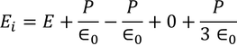 ………..(22)
………..(22)
Hence the Internal field obtained is
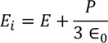 ………..(23)
………..(23)
Claussius -Mosotti Equation
It gives the relation between the dielectric constant and the ionic polarizability of atoms in dielectric material. If there are N number of atoms, the dipole moment per unit volume which is called Polarization is given by,
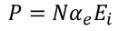 ………..(24)
………..(24)
We know internal field
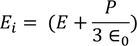 ………..(25)
………..(25)
From above equations

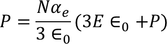
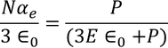 ………..(26)
………..(26)
We know polarization from the relation between polarization and dielectric constant
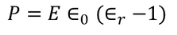 ………..(27)
………..(27)
From the above two equations we get,
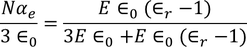
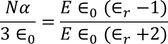
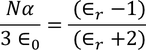 ………..(28)
………..(28)
11 Question: Write a note on Ferroelectrics?
Solution:
Ferroelectrics
Ferroelectricity was first discovered in 1921 in a complex compound called Rochelle salt (Sodium potassium tartrate tetrahydrate). At that time it was the only material possessing the extraordinary property of reversible polarization. Later around 1935 ferroelectricity was observed in potassium dihydrogen phosphate (KH2PO4). The most popular and classical ferroelectric material BaTiO3 was discovered during World War II in 1941. BaTiO3 originally looked as a potential material for capacitors because of its high dielectric constant.
The high dielectric constant originates from the ferroelectric nature of BaTiO3. The physical quantity corresponding to the stored electric energy per unit area is called electric displacement D; it is related to the electric field E by the following simple expression
D= ε0E +P = εε0E
Where ε and ε0 are the material’s relative permittivity and permittivity of the vacuum respectively and P is the dielectric polarization, respectively.
When the centre of the positive and negative charges in the crystal structure do not coincide naturally (without application of any external field) such crystals are said to possess a spontaneous polarization. When, upon applying an electric field, such a spontaneous polarization can be reversed then the material is called ferroelectric.
Ferroelectrics are simply defined as the “class of materials which exhibits spontaneous electric polarization (in the absence of electric field) which reversible by applying an electric field”.
The term ferro in the ferroelectrics has nothing to do with the ferrous i.e., iron content in the materials, rather this term used to explain that this class of materials exhibit spontaneous electric polarization and electric hysteresis, analogous to the ferromagnetic properties of spontaneous magnetization and magnetic hysteresis.
The ferroelectric nature of a material depends crucially on the atomic structure. Other ferroelectric materials are Lead zirconate titanate (PZT), Lead lanthanum zirconate titanate (PLZT), Lithium niobate (LiNbO3), and relaxors like Lead magnesiumniobate (PMN).
12 Question: Write a note on Piezoelectric?
Solution:
Piezoelectric
All ferroelectric materials are piezoelectric (but the reverse is not true). In Piezoelectric “Piezo” derived from the Greek word “piezein” and the meaning of piezein is squeeze or press. So its name itself explaining the effect.
Direct Piezoelectric Effect
The piezoelectric effect transforms kinetic or mechanical energy into electrical energy, due to crystal deformation. When the material is compressed or squeezed, this Mechanical stress applied to the material generates electricity.
Microphones, speakers, buzzers, pressure sensors, hydrophones, and many other sensing types of devices use direct piezoelectric effect.
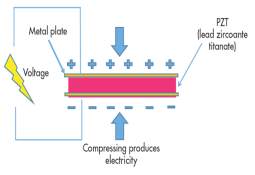
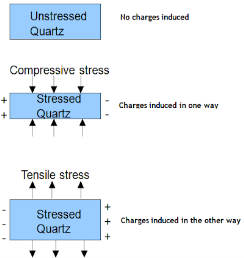
The above figure shows the direct piezoelectric effect
Figure 29: Direct Piezoelectric Effect
Inverse Piezoelectric Effect
We can reverse the same effect. Inverse piezoelectric effect – when an electric field is applied to a crystal it aligns all dipoles present in the material in order. This realignment results in deformation of crystal i.e. converting electrical energy into kinetic or mechanical energy. The reversal of the piezoelectric effect is called the inverse piezoelectric effect.
Using the inverse piezoelectric effect we can develop devices that produce acoustic sound waves. Even medical ultrasound and sonar transducers use the inverse piezoelectric effect.
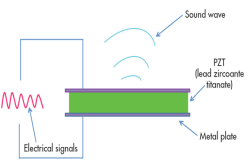
The above figure shows the inverse piezoelectric effect
Figure 30: The Inverse Piezoelectric Effect
The basic equations describing the direct and converse piezoelectric effects can be expressed in terms of electric and elastic properties as follows
D = dE + εσE
S = sEσ + dE
Where D is the dielectric displacement, σ the stress, E the electric field, S the strain, d the piezoelectric coefficient, s the material compliance constant (inverse of the elastic constant) and ε is the material’s dielectric constant (permittivity). The superscript in the equations indicates that the quantity is held constant. In the case of εσ stress is held constant which implies that the piezoelectric element is mechanically unconstrained and in the case of sE, the electric field is held constant which implies electrodes on the elements are mutually shortened.
The direct and converse piezoelectric effects can also be conveniently expressed in terms of following tensor notations:
Pi = dijkσjk
Xij = dkijEk
In case of the direct piezoelectric effect Pi is the polarization generated along the i-axis, which is proportional to the applied stress σjk through the piezoelectric coefficients dijk. For the converse piezoelectric effect Xij is the strain generated in a particular orientation of the crystal when an electric field Ek is applied along a certain k-axis.
Examples of Piezoelectric Materials
All piezoelectric materials are non-conductive for the piezoelectric effect to occur and work. Quartz is natural and first Piezoelectric Material whereas Lead Zirconate Titanate, Barium Titanate, and Lithium Niobate are man-made Piezoelectric Materials.
Q.13 Define Magnetic susceptibility (χ)
Solution:
If H is the applied magnetizing field intensity and M is the amount of magnetization of the material,
Then χ = 
χ = 0 in vacuum
χ = +ve for paramagnetic and Ferro magnetic materials
χ = -ve for diamagnetic materials
Units: It has no units.
Q.14 How can we Classify Magnetic Materials?
Solution:
Magnetic materials are classified as follows:
- Diamagnetic
- Paramagnetic
- Ferromagnetic
- Anti-Ferro magnetic
- Ferric magnetic or ferrites
Diamagnetic
The orbital motion of electrons around the nucleus produces a magnetic field perpendicular to the plane of the orbit. Thus each electron orbit has a finite orbital magnetic dipole moment. Since the orbital planes are oriented randomly, the vector sum of magnetic moments is zero and there is no resultant magnetic moment for each atom.
In the presence of an external magnetic field, some electrons are speeded up and some are slowed down. The electrons whose moments were anti-parallel are speeded up according to Lenz’s law and this produces an induced magnetic moment in a direction opposite to the field. The induced moment disappears as soon as the external field is removed.
When placed in a non-uniform magnetic field, the interaction between the induced magnetic moment and the external field creates a force that tends to move the material from the stronger part to the weaker part of the external field. It means that diamagnetic material is repelled by the field.
This action is called diamagnetic action and such materials are known as diamagnetic materials. Examples: Bismuth, Copper, and Water, etc.
The properties of diamagnetic materials are
- Magnetic susceptibility is negative.
- Relative permeability is slightly less than unity.
- The magnetic field lines are repelled or expelled by diamagnetic materials when placed in a magnetic field.
- Susceptibility is nearly temperature independent.
- Examples: Cu, Au, Zn, H20, Bi, etc. organic materials
Paramagnetic materials
In some magnetic materials, each atom or molecule has a net magnetic dipole moment which is the vector sum of orbital and spin magnetic moments of electrons. Due to the random orientation of these magnetic moments, the net magnetic moment of the materials is zero.
In the presence of an external magnetic field, the torque acting on the atomic dipoles will align them in the field direction. As a result, there is a net magnetic dipole moment induced in the direction of the applied field. The induced dipole moment is present as long as the external field exists.
The properties of paramagnetic materials are:
- Magnetic susceptibility is positive and small.
- Relative permeability is greater than unity.
- The magnetic field lines are attracted to the paramagnetic materials when placed in a magnetic field.
- Susceptibility is inversely proportional to temperature.
Ferromagnetic materials
An atom or a molecule in a ferromagnetic material possesses a net magnetic dipole moment as in a paramagnetic material. A ferromagnetic material is made up of smaller regions, called ferromagnetic domain. Within each domain, the magnetic moments are spontaneously aligned in a direction. This alignment is caused by strong interaction arising from electron spin which depends on the inter-atomic distance. Each domain has net magnetization in a direction. However, the direction of magnetisation varies from domain to domain and thus net magnetisation of the specimen is zero.
In the presence of an external magnetic field, two processes take place
1. The domains having magnetic moments parallel to the field grow in size
2. The other domains (not parallel to the field) are rotated so that they are aligned with the field.
As a result of these mechanisms, there is a strong net magnetisation of the material in the direction of the applied field
When placed in a non-uniform magnetic field, the ferromagnetic materials will have a strong tendency to move from the weaker to the stronger part of the field. Materials that exhibit strong magnetism in the direction of the applied field are called ferromagnetic materials. Examples: Iron, Nickel, and Cobalt.
The properties of ferromagnetic materials are:
- Magnetic susceptibility is positive and large.
- Relative permeability is large.
- The magnetic field lines are strongly attracted to the ferromagnetic materials when placed in a magnetic field.
- Susceptibility is inversely proportional to temperature.
Antiferromagnetism
In the periodic table, the only element exhibiting antiferromagnetism at room temperature is chromium. Antiferromagnetic materials are very similar to ferromagnetic materials but the exchange interaction between neighboring atoms leads to the anti-parallel alignment of the atomic magnetic moments. Therefore, the magnetic field cancels out and the material appears to behave in the same way as a paramagnetic material. Like ferromagnetic materials, these materials become paramagnetic above a transition temperature, known as the Neel temperature, TN. (Cr: TN=37ºC).
The properties of antiferromagnetic materials are:
- They have permanent magnetic dipoles
- They do not possess a permanent magnetic dipole moment. Since in the absence of field, they have no spontaneous magnetization due to anti-parallel spin
- The relative permeability μr>1
- Susceptibility χ is small but negative
- 𝜒depends on temperature
Q.15 Discuss in brief the B-H curve?
Solution:
Magnetic Hysteresis
The lag or delay of a magnetic material known commonly as Magnetic Hysteresis relates to the magnetization properties of a material by which it first becomes magnetized and then de-magnetized.
The set of magnetization curves, M above represents an example of the relationship between B and H for soft-iron and steel cores but every type of core material will have its own set of magnetic hysteresis curves. You may notice that the flux density increases in proportion to the field strength until it reaches a certain value where it cannot increase any more becoming almost level and constant as the field strength continues to increase.
This is because there is a limit to the amount of flux density that can be generated by the core as all the domains in the iron are perfectly aligned. Any further increase will not affect the value of M, and the point on the graph where the flux density reaches its limit is called Magnetic Saturation also known as Saturation of the Core and in our simple example above the saturation point of the steel, the curve begins at about 3000 ampere-turns per metre.
As the magnetic field strength, ( H ) increases these molecular magnets become more and more aligned until they reach perfect alignment producing maximum flux density, and an increase in the magnetic field strength due to an increase in the electrical current flowing through the coil will have little or no effect.
Retentivity
Let’s assume that we have an electromagnetic coil with a high field strength due to the current flowing through it and that the ferromagnetic core material has reached its saturation point, maximum flux density. If we now open a switch and remove the magnetizing current flowing through the coil we would expect the magnetic field around the coil to disappear as the magnetic flux reduced to zero.
However, the magnetic flux does not completely disappear as the electromagnetic core material still retains some of its magnetism even when the current has stopped flowing in the coil. This ability for a coil to retain some of its magnetism within the core after the magnetization process has stopped is called Retentivity or remanence, while the amount of flux density remaining in the core is called Residual Magnetism, BR.
The reason for this that some of the tiny molecular magnets do not return to a completely random pattern and still point in the direction of the original magnetizing field giving them a sort of “memory”. Some ferromagnetic materials have a high retentivity (magnetically hard) making them excellent for producing permanent magnets.
While other ferromagnetic materials have low retentivity (magnetically soft) making them ideal for use in electromagnets, solenoids, or relays. One way to reduce this residual flux density to zero is by reversing the direction of the current flowing through the coil, thereby making the value of H, the magnetic field strength negative. This effect is called a Coercive Force, HC.
If this reverse current is increased further the flux density will also increase in the reverse direction until the ferromagnetic core reaches saturation again but in the reverse direction from before. Reducing the magnetizing current, i once again to zero will produce a similar amount of residual magnetism but in the reverse direction.
Then by constantly changing the direction of the magnetizing current through the coil from a positive direction to a negative direction, as would be the case in an AC supply, a Magnetic Hysteresis loop of the ferromagnetic core can be produced.

Figure 2
The B-H Curve or Magnetic Hysteresis loop above shows the behaviour of a ferromagnetic core graphically as the relationship between B and H is non-linear.
Starting with an unmagnetized core both B and H will be at zero, point 0 on the magnetization curve.
If the magnetization current, i is increased in a positive direction to some value the magnetic field strength H increases linearly with i and the flux density B will also increase as shown by the curve from point 0 to point a as it heads towards saturation.
Now if the magnetizing current in the coil is reduced to zero, the magnetic field circulating around the core also reduces to zero. However, the coils magnetic flux will not reach zero due to the residual magnetism present within the core and this is shown on the curve from point a to point b.
To reduce the flux density at point b to zero we need to reverse the current flowing through the coil. The magnetising force which must be applied to null the residual flux density is called a “Coercive Force”. This coercive force reverses the magnetic field re-arranging the molecular magnets until the core becomes unmagnetised at point c.
An increase in this reverse current causes the core to be magnetised in the opposite direction and increasing this magnetisation current further will cause the core to reach its saturation point but in the opposite direction, point d on the curve.
This point is symmetrical to point b. If the magnetising current is reduced again to zero the residual magnetism present in the core will be equal to the previous value but in reverse at point e.
Again reversing the magnetising current flowing through the coil this time into a positive direction will cause the magnetic flux to reach zero, point f on the curve and as before increasing the magnetisation current further in a positive direction will cause the core to reach saturation at point a.
Then the B-H curve follows the path of a-b-c-d-e-f-a as the magnetising current flowing through the coil alternates between a positive and negative value such as the cycle of an AC voltage. This path is called a B-H Curve or Magnetic Hysteresis Loop.
The effect of magnetic hysteresis shows that the magnetisation process of a ferromagnetic core and therefore the flux density depends on which part of the curve the ferromagnetic core is magnetised on as this depends upon the circuits past history giving the core a form of “memory”. Then ferromagnetic materials have memory because they remain magnetised after the external magnetic field has been removed.
However, soft ferromagnetic materials such as iron or silicon steel have very narrow magnetic hysteresis loops resulting in very small amounts of residual magnetism making them ideal for use in relays, solenoids, and transformers as they can be easily magnetised and demagnetised.
Since a coercive force must be applied to overcome this residual magnetism, work must be done in closing the hysteresis loop with the energy being used being dissipated as heat in the magnetic material. This heat is known as hysteresis loss, the amount of loss depends on the material’s value of coercive force.
By adding additives to the iron metal such as silicon, materials with a very small coercive force can be made that have a very narrow hysteresis loop. Materials with narrow hysteresis loops are easily magnetised and demagnetised and known as soft magnetic materials.
Q.16 Draw B-H Curve for Soft and Hard Materials?
Solution:
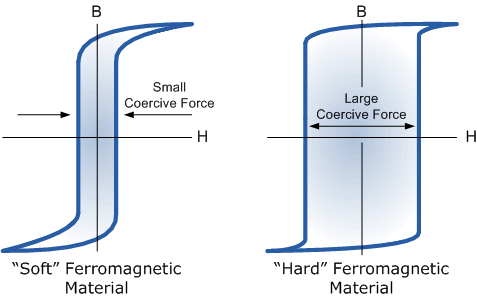
Figure 3
The shape of the hysteresis loop depends upon the nature of the iron or steel used and in the case of iron which is subjected to massive reversals of magnetism, for example, transformer cores, the B-H hysteresis loop must be as small as possible.