Question Bank (unit-5)
Question-1: evaluate
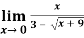
Sol.
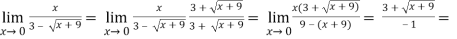 -6.
-6.
Question-2: Test the continuity of the following function-
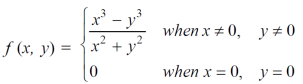
Sol. (1) the function is well defined at (0,0)
(2) check for the second step,
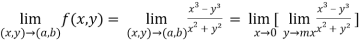
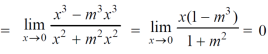
That means the limit exists at (0,0)
Now check step-3:
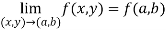

So that the function is continuous at origin.
Question-3: Evaluate 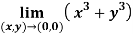
Sol . 1. 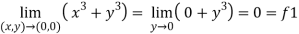
2. 
Here f1 = f2
3. Now put y = mx, we get
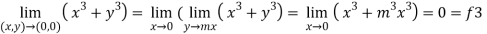
Here f1 = f2 = f3
Now put y = mx²
4. 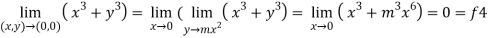
Therefore ,
F1 = f2 = f3 =f4
We can say that the limit exists with 0.
Question-4: evaluate the following-
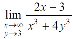
Sol. First we will calculate f1 –

Here we see that f1 = 0
Now find f2,
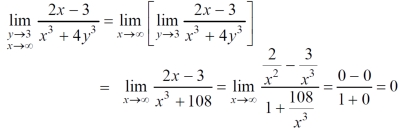
Here , f1 = f2
Therefore the limit exists with value 0.
Question-5: Calculate 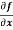 and
and  for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate  treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
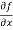 =
=  [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] -  5y²] +
5y²] + 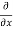 [2xy] -
[2xy] - 8x] +
8x] +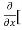 4y] -
4y] -  20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
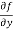 =
= 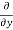 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
=  3x³] -
3x³] -  5y²] +
5y²] +  [2xy] -
[2xy] -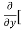 8x] +
8x] + 4y] -
4y] - 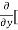 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Question-6: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Sol.  3x²y² - y⁵,
3x²y² - y⁵,  2x³y – 5xy⁴,
2x³y – 5xy⁴,
 =
= 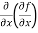 = 6xy²
= 6xy²
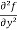 =
=  2x³ - 20xy³
2x³ - 20xy³
 =
= 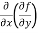 = 6x²y – 5y⁴
= 6x²y – 5y⁴
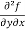 =
= 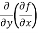 = 6x²y - 5y⁴
= 6x²y - 5y⁴
Question-7: if 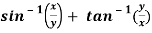 , then show that-
, then show that- 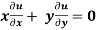
Sol. Here we have,
u = 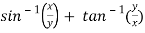 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get

= 
Or
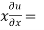
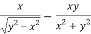 ………………..(2)
………………..(2)
And now,

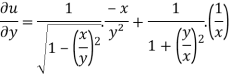
= 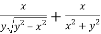
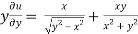 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get

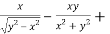
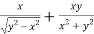 = 0
= 0
Hence proved.
Question-8: If u = x²(y-x) + y²(x-y), then show that 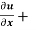
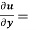 -2 (x – y)²
-2 (x – y)²
Solution - here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
now differentiate u partially with respect to x and y respectively,
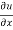 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
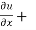
 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Question-9: If u(x,y,z) = log( tan x + tan y + tan z) , then prove that ,

Sol. Here we have,
u(x,y,z) = log( tan x + tan y + tan z) ………………..(1)
Diff. Eq.(1) w.r.t. x , partially , we get

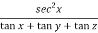 ……………..(2)
……………..(2)
Diff. Eq.(1) w.r.t. y , partially , we get

 ………………(3)
………………(3)
Diff. Eq.(1) w.r.t. z , partially , we get

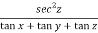 ……………………(4)
……………………(4)
Now multiply eq. 2 , 3 , 4 by sin 2x , sin 2y , sin 2z respectively and adding , in order to get the final result,
We get,
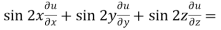
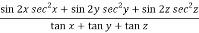

= 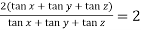
So that,
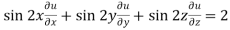 hence proved.
hence proved.
Question-10: let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find  .
.
Sol. : 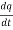 . =
. = 
Where, f1 =  , f2 =
, f2 = 
In this example f1 = 4 , f2 = 3
Also, 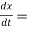 3t² + 2t ,
3t² + 2t , 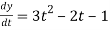
 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(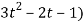
= 21t² + 2t – 3
Question-11: if w = x² + y – z + sint and x + y = t, find
(a) 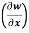 y,z
y,z
(b) 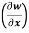 t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x² + y - z + sin (x + y).
Therefore,
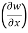 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)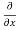 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
thus  t, z = 2x – 1
t, z = 2x – 1
Question-12: : if φ( cx – az , cy – bz) = 0 then show that ap + bq = c
Where p = 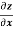 q =
q = 
Sol. We have,
φ( cx – az , cy – bz) = 0
φ( r , s) = 0
Where,

We know that,
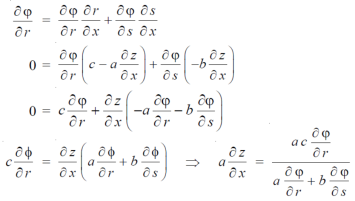
Again we do,

By adding the two results, we get


Question-13: If z is the function of x and y , and x = 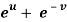 , y =
, y = 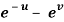 , then prove that,
, then prove that,
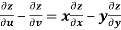
Sol. Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
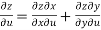 ……………….(1)
……………….(1)
And,
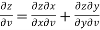 ………………..(2)
………………..(2)
Also there is,
x = 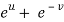 and y =
and y = 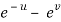 ,
,
Now,
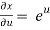 ,
, 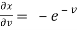 ,
, 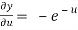 ,
, 
From equation(1) , we get
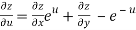 ……………….(3)
……………….(3)
And from eq. (2) , we get
 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
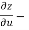
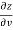 =
=  )
)  – (
– (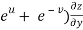
= x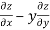
Hence proved.
Question-14: If x = r sin , y = r sin
, y = r sin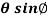 , z = r cos
, z = r cos , then show that
, then show that
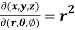 sin
sin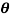 also find
also find 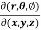
Sol. We know that,
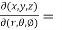

= 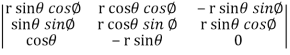
= 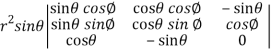
= 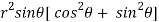 ( on solving the determinant)
( on solving the determinant)
= 
Now using first propert of Jacobians, we get
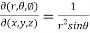
Question-15: If u = xyz , v = x² + y² + z² and w = x + y + z, then find J = 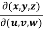
Sol. Here u ,v and w are explicitly given , so that first we calculate
J’ = 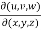
J’ = 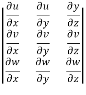 =
= 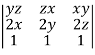
= yz(2y-2z) – zx(2x – 2z) + xy (2x – 2y) = 2[yz(y-z)-zx(x-z)+xy(x-y)]
= 2[x²y - x²z - xy² + xz² + y²z - yz²]
= 2[x²(y-z) - x(y² - z²) + yz (y – z)]
= 2(y – z)(z – x)(y – x)
= -2(x – y)(y – z)(z – x)
By the property,
JJ’ = 1
J = 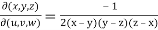
Question-16: Prove that the following functions are functionally dependent.
f(x , y) = log x – log y and g(x , y) = 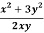
Sol. We have,
f(x , y) = log x – log y …………………(1)
g(x , y) =  …………………………(2)
…………………………(2)
Here we will find x from the second equation and substitute in (1) , which will show the relation between the two.
Write f(x,y) = f and g(x,y) = g for convenience,
From equation(1) , we get
2g.xy = 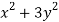
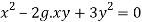

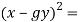

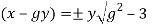
Lets consider,

x = y [ g + 
Put this value in eq.(1), we get
f = log x – log y
= log y [ g +  – log y
– log y
= log y + log y ( g + 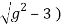 – log y
– log y
f = log (g + 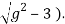
The functional relationship F(u,v) = 0 is,
F(u,v) = u - log (v + 
Now we can verify that,
F(f(x,y) , g(x,y)) = 0
The jacobian will also be zero.
Question-17: The temperature T at any point 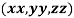 in space is
in space is 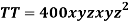 .Find the highest temperature on the surface of the unit sphere.
.Find the highest temperature on the surface of the unit sphere.
Sol. Given function is 
On the surface of unit sphere given  [
[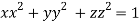 is an equation of unit sphere in 3 dimensional space]
is an equation of unit sphere in 3 dimensional space]
By Lagrange’s Method
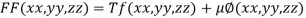
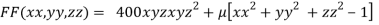 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
 or
or 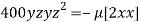 …(ii)
…(ii)
 or
or 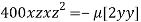 …(iii)
…(iii)
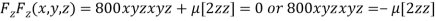 …(iv)
…(iv)
Dividing (ii) and (ii) by (iv) we get
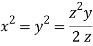
Using given relation 
Or 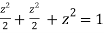 Or
Or 
So that 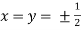
Or 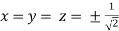
Thus points are 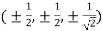
The maximum temperature is 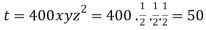
Question-18: Find the points on the surface  nearest to the origin.
nearest to the origin.
Sol.
Let  be any point on the surface, then its distance from the origin
be any point on the surface, then its distance from the origin 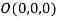 is
is

Thus the given equation will be
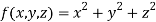
And relation is 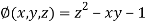
By Lagrange’s Method

 ….(i)
….(i)
Partially differentiatig (i) with respect to x, y and z and equate them to zero
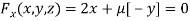
Or 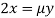 …(ii)
…(ii)

Or 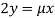 …(iii)
…(iii)
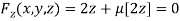
Or 
Or 
On solving equation (ii) by (iii) we get
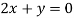
And 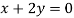
On subtracting we get 
Putting in above 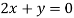
 Or
Or 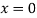
Thus 
Using the given relation we get
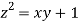 = 0.0 +1=1
= 0.0 +1=1
Or 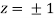
Thus point on the surface nearest to the origin is 