Unit - 6

Recursion and Structure

Q1) What is recursion give an example?

A1)

Recursion is the process which comes into existence when a function calls a copy of itself to work on a smaller problem. Any function which calls itself is called recursive function, and such function calls are called recursive calls. Recursion involves several numbers of recursive calls. However, it is important to impose a termination condition of recursion. Recursion code is shorter than iterative code however it is difficult to understand.

Recursion cannot be applied to all the problem, but it is more useful for the tasks that can be defined in terms of similar subtasks. For Example, recursion may be applied to sorting, searching, and traversal problems.

Generally, iterative solutions are more efficient than recursion since function call is always overhead. Any problem that can be solved recursively, can also be solved iteratively. However, some problems are best suited to be solved by the recursion, for example, tower of Hanoi, Fibonacci series, factorial finding, etc.

In the following example, recursion is used to calculate the factorial of a number.

1. #include <stdio.h>  
2. Int fact (int);  
3. Int main()  
4. {  
5.    Int n,f;  
6.    Printf("Enter the number whose factorial you want to calculate?");  
7.    Scanf("%d",&n);  
8.    f = fact(n);  
9.    Printf("factorial = %d",f);  
10. }  
11. Int fact(int n)  
12. {  
13.    If (n==0)  
14.    {  
15.        Return 0;  
16.    }  
17.    Else if ( n == 1)  
18.    {  
19.        Return 1;  
20.    }  
21.    Else   
22.    {  
23.        Return n*fact(n-1);  
24.    }  
25. }  

Output

Enter the number whose factorial you want to calculate?5

Factorial = 120

We can understand the above program of the recursive method call by the figure given below:

Q2) What is Recursive Function?

A2)

A recursive function performs the tasks by dividing it into the subtasks. There is a termination condition defined in the function which is satisfied by some specific subtask. After this, the recursion stops and the final result is returned from the function.

The case at which the function doesn't recur is called the base case whereas the instances where the function keeps calling itself to perform a subtask, is called the recursive case. All the recursive functions can be written using this format.

Pseudocode for writing any recursive function is given below.

1. If (test_for_base)  
2. {  
3.    Return some_value;  
4. }  
5. Else if (test_for_another_base)  
6. {  
7.    Return some_another_value;  
8. }  
9. Else  
10. {  
11.    // Statements;  
12.    Recursive call;  
13. }  

Q3) Write an example of recursion in C

A3)

Let's see an example to find the nth term of the Fibonacci series.

1. #include<stdio.h>  
2. Int fibonacci(int);  
3. Void main ()  
4. {  
5.    Int n,f;  
6.    Printf("Enter the value of n?");  
7.    Scanf("%d",&n);  
8.    f = fibonacci(n);  
9.    Printf("%d",f);  
10. }  
11. Int fibonacci (int n)  
12. {  
13.    If (n==0)  
14.    {  
15.    Return 0;  
16.    }  
17.    Else if (n == 1)  
18.    {  
19.        Return 1;   
20.    }  
21.    Else  
22.    {  
23.        Return fibonacci(n-1)+fibonacci(n-2);  
24.    }  
25. }  

Output

Enter the value of n?12

144

Q4) Explain Memory allocation of Recursive method

A4)

Each recursive call creates a new copy of that method in the memory. Once some data is returned by the method, the copy is removed from the memory. Since all the variables and other stuff declared inside function get stored in the stack, therefore a separate stack is maintained at each recursive call. Once the value is returned from the corresponding function, the stack gets destroyed. Recursion involves so much complexity in resolving and tracking the values at each recursive call. Therefore we need to maintain the stack and track the values of the variables defined in the stack.

Let us consider the following example to understand the memory allocation of the recursive functions.

1. Int display (int n)  
2. {  
3.    If(n == 0)  
4.        Return 0; // terminating condition  
5.    Else   
6.    {  
7.        Printf("%d",n);  
8.        Return display(n-1); // recursive call  
9.    }  
10. }  

Explanation

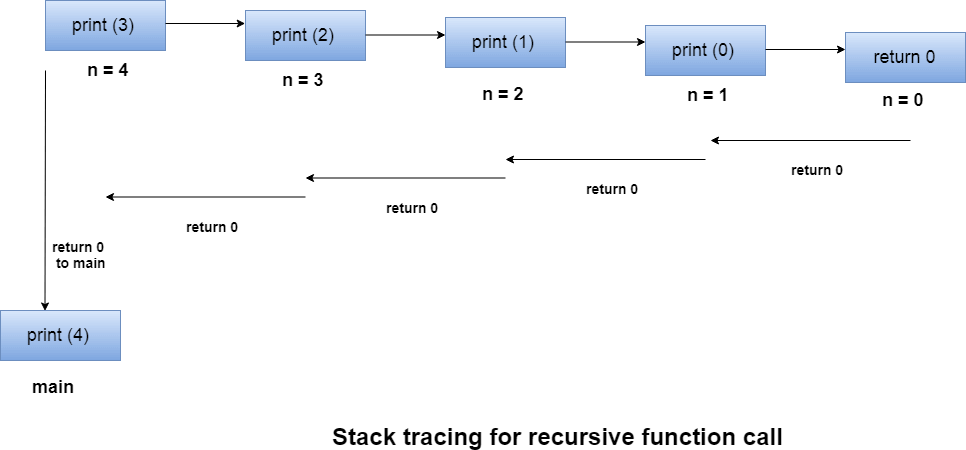
Let us examine this recursive function for n = 4. First, all the stacks are maintained which prints the corresponding value of n until n becomes 0, Once the termination condition is reached, the stacks get destroyed one by one by returning 0 to its calling stack. Consider the following image for more information regarding the stack trace for the recursive functions.

Q5) Give an example of Recursion as a different way of solving problems

A5)

Recursion is a common form of the general-purpose problem-solving technique called divide and conquer''. The principle of divide-and-conquer, is that you solve a given problem P in 3 steps:

1. Divide P into several subproblems, P1,P2,...Pn.
2. Solve, however you can, each of the subproblems to get solutions S1...Sn.
3. Use S1...Sn to construct a solution to the original problem, P.

This is often recursive, because in order to solve one or more of the subproblems, you might use this very same strategy. For instance, you might solve P1 be subdividing it into P1a,P1b..., solving each one of them, and putting together their solutions to get the solution S1 to problem P1.

An Everyday Example

To give a simple example, suppose you want to solve this problem:

P = carry a pile of 50 books from your office to your car.

Well, you can't even lift such a big pile, never mind carry it. So you split the original pile into 3 piles:

P1 contains 10 books, P2 contains 15 books, P3 contains 25 books.

Your plan, of course, is to carry each pile to the car separately, and then put them back together into one big pile once they are all there. This is a recursive divide-and-conquer strategy; you have divided the original problem P into 3 problems of the same kind.

Now suppose you can directly solve P1 and P2 - they are small enough that you can carry them to the car. So, P1 and P2 are now sitting out there by the car. Once you get P3 there, you will pile them up again.

But P3 is too big to be carried. You apply the same strategy recursively: divide P3 into smaller problems, solve them, and combine the results to make the solution for P3. You divide P3 into two piles, P3a has 11 books, P3b has 14, and carry these separately to the car. Then you put P3a back onto P3b to form the pile P3 there at the car.

Now you have solved all the subproblems: P1, P2, P3 are sitting at the car. You stack them into one big pile, and presto, you have solved the original problem.

This may seem like a rather hokey example, but it illustrates very well the principles of divide-and-conquer. Let us see how we can use the very same ideas to solve mathematical and computer science problems.

Q6) Write a Mathematical Example of Recursion as a different way of solving problems

A6)

Find an algorithm for raising a number X to the power N, where N is a positive integer. You may use only two operations: multiplication, subtraction. We would like to multiply N copies of X all at once, but, like the piles of books, we do not have an operation that directly allows us to do that: we can only multiply two numbers at a time. In other words, the problems we can solve directly are these:

• Raise X to the power 1: answer = X.
• Raise X to the power 2: answer = X * X.

Any other problem we have to solve indirectly, by breaking it down into smaller and smaller problems until we have reduced it to one of these base cases.

So, if N > 2, we split the original problem into two subproblems:

• P1: raise X to the power I. The answer to this is S1.
• P2: raise X to the power N-I. The answer to this is S2.
• To get the final answer, S, combine S1 and S2: S = S1 * S2.

How do we solve P1 and P2? They are problems of exactly the same type as original problem, so we can apply to them exactly the same strategy that we applied to the original problem. We check to see if we can solve them directly... If I=1 or I=2 we can solve P1 directly; if N-I=1 or N-I=2 we can solve P2 directly. The problems we cannot solve directly, we solve recursively, as just described. An interesting feature of this strategy is that it works no matter how we split up N.

We can't directly solve this problem, so we divide it into:

• P1: raise 3 to the power 2. (choose I=2, no particular reason)
• P2: raise 3 to the power 5.

We can directly solve P1, the answer is S1 = 9. But P2 we have to further decompose:

• P2.1: raise 3 to the power 1. (choose I=1, no particular reason)
• P2.2: raise 3 to the power 4.

Again, P2.1 can be directly solved, S2.1 = 3, but P2.2 must be further decomposed:

• P2.2.1: raise 3 to the power 2.
• P2.2.2: raise 3 to the power 2.

These both can be directly solved; S2.2.1 = S2.2.2 = 9. These are combined to give S2.2 = 9*9 = 81.

Now that we have the solutions to P2.1 and P2.2 we combine them to get the solution to P2, S2 = 3*81 = 243.

Now that we have solutions for P1 and P2, we combine them to get the final solution, S = S1*S2 = 9*243 = 2187.

I said that the strategy would work no matter how we chose to subdivide the problem: any choice of I' will give the correct answer. However, some choices of I' compute the final answer faster than others. Which do you think is faster: choosing I=1 (every time) or I=2?

Answer: The computation will be faster if you choose I=2 because there will be half the number of recursive calls, and therefore half the overhead.

This is true of most recursive strategies: they usually work correctly for many different ways of decomposing the problem, but some ways are much more efficient than others. In our first example, we also were free to divide the pile of books into as many piles and whatever sizes we liked. But it obviously would be very inefficient to carry one book at a time.

Q7) Explain structure in detail

A7)

A structure can be considered as a template used for defining a collection of variables under a single name. Structures help programmers to group elements of different data types into a single logical unit (Unlike arrays which permit a programmer to group only elements of same data type).

Why Use Structures

•         Ordinary variables can hold one piece of information

•         arrays can hold a number of pieces of information of the same data type.

For example, suppose you want to store data about a book. You might want to store its name (a string), its price (a float) and number of pages in it (an int).

If data about say 3 such books is to be stored, then we can follow two approaches:

      Construct individual arrays, one for storing names, another for storing prices and still another for storing number of pages.

      Use a structure variable.

Suppose we want to create a employee database. Then, we can define a structure

Called employee with three elements id, name and salary. The syntax of this structure is as

Follows:

Struct employee  

{   int id;  

Char name[50];  

Float salary;  

};

Note:

      Struct keyword is used to declare structure.

      Members of structure are enclosed within opening and closing braces.

      Usually structure type declaration appears at the top of the source code file, before any variables or functions are defined or maintained in separate header file.

      Declaration of Structure reserves no space.

      It is nothing but the “Template / Map / Shape” of the  structure .

      Memory is created, very first time when the variable is created / Instance is created.

Structure variable declaration:

We can declare the variable of structure in two ways

1. Declare the structure inside main function
2. Declare the structure outside the main function.

1. Declare the structure inside main function

Following example show you, how structure variable is declared inside main function

Struct employee  

{  

Int id;  

Char name[50];  

Float salary;  

};  

Int main()

{

Struct employee e1, e2; 

Return 0;

}

In this example the variable of structure employee is created inside main function that e1, e2.

2. Declare the structure outside main function

Following example show you, how structure variable is declared outside the main function

Struct employee  

{  

Int id;  

Char name[50];  

Float salary;  

}e1,e2;  

Q8) Explain Memory allocation for structure

A8)

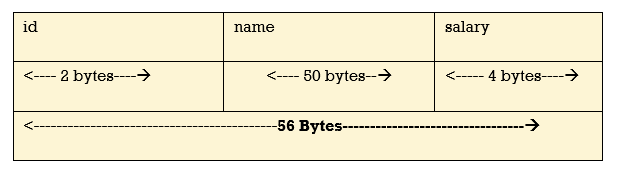
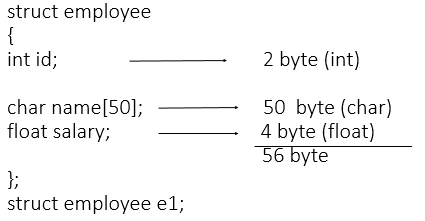
Memory is allocated to the structure only when we create the variable of structure.

Consider following example

Q9) Explain Structure Initialization in different ways

A9)

1. When we declare a structure, memory is not allocated for un-initialized variable.

2. Let us discuss very familiar example of structure student , we can initialize structure variable

In different ways –

Way 1: Declare and Initialize

Struct student

{

Char name[20];

Int roll;

Float marks;

}std1 = { "Poonam",89,78.3 };

In the above code snippet, we have seen that structure is declared and as soon as after declaration we

Have initialized the structure variable.

Std1 = { "Poonam",89,78.3 }

This is the code for initializing structure variable in C programming

Way 2: Declaring and Initializing Multiple Variables

Struct student

{

Char name[20];

Int roll;

Float marks;

}

Std1 = {"Poonam" ,67, 78.3};

Std2 = {"Vishal",62, 71.3};

In this example, we have declared two structure variables in above code. After declaration of variable we have initialized two variable.

Std1 = {"Poonam" ,67, 78.3};

Std2 = {"Vishal",62, 71.3};

Way 3: Initializing Single member

Struct student

{

Int mark1;

Int mark2;

Int mark3;

} sub1={67};

Though there are three members of structure, only one is initialized , Then remaining two members

Are initialized with Zero. If there are variables of other data type then their initial values will be –

Q10) Explain Array within Structure with example

A10)

As we know, structure is collection of different data type. Like normal data type, It can

Also store an array as well.

Syntax for array within structure

Struct struct-name

{

Datatype var1; // normal variable

Datatype array [size]; // array variable

- - - - - - - - - -

- - - - - - - - - -

Datatype varN;

};

Struct struct-name obj;

Example for array within structure

Struct Student

{

Int Roll;

Char Name[25];

Int Marks[3]; //Statement 1 : array of marks

Int Total;

Float Avg;

};

Void main()

{

Int i;

Struct Student S;

Printf("\n\nEnter Student Roll : ");

Scanf("%d",&S.Roll);

Printf("\n\nEnter Student Name : ");

Scanf("%s",&S.Name);

S.Total = 0;

For(i=0;i<3;i++)

{

Printf("\n\nEnter Marks %d : ",i+1);

Scanf("%d",&S.Marks[i]);

S.Total = S.Total + S.Marks[i];

}

S.Avg = S.Total / 3;

Printf("\nRoll : %d",S.Roll);

Printf("\nName : %s",S.Name);

Printf("\nTotal : %d",S.Total);

Printf("\nAverage : %f",S.Avg);

}

Output:

Enter Student Roll : 10

Enter Student Name : Kumar

Enter Marks 1 : 78

Enter Marks 2 : 89

Enter Marks 3 : 56

Roll : 10

Name : Kumar

Total : 223

Average : 74.00000

In the above example, we have created an array Marks[ ] inside structure representing 3 marks of a single student. Marks[ ] is now a member of structure student and to access Marks[ ] we have used dot operator(.) along with object S.