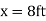Unit – 3
Moment of Inertia about an axis and polar moment of inertia
Q1) Prepare a chart of Moment of inertia about an axis and polar moment of inertia for different shapes.
A1)
Shape | Area(a) | Moment of Inertia | Radius of gyration (r) | Polar moment of Inertia (J) |
Rectangle 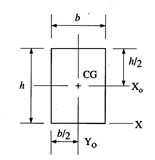 |  | 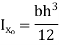 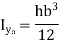 
|  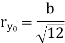 
| 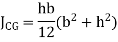 |
Triangle 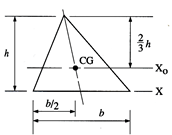 |  | 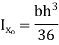 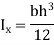
|  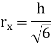
|
|
Circle 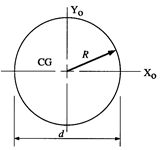 | 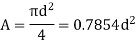 | 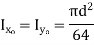 | 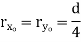 |  |
Semicircle  | 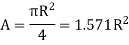 | 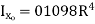 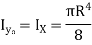 | 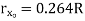 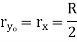 |   |
Hollow circle 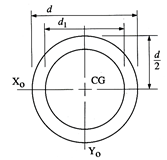 | 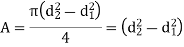 | 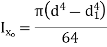 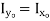 | 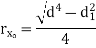 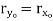 | 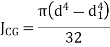 |
Hollow rectangle  |  | 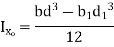  |  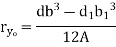 | 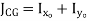 |
Quarter circle  | 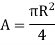 | 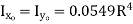 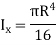 | 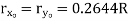 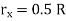 | 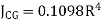 |
Q2) Describe Deflection of beam using double integration method.
A2)
Assumption: The following assumptions are undertaken in order to derive a differential equation of elastic curve for the loaded beam
1. Stress is proportional to strain i.e., hooks law applies. Thus, the equation is valid only for beams that are not stressed beyond the elastic limit.
2. The curvature is always small.
3. Any deflection resulting from the shear deformation of the material or shear stresses is neglected.
It can be shown that the deflections due to shear deformations are usually small and hence can be ignored.

Consider a beam AB which is initially straight and horizontal when unloaded. If under the action of loads the beam deflect to a position A’B’ under load or infact we say that the axis of the beam bends to a shape A’B’. It is customary to call A’B’ the curved axis of the beam as the elastic line or deflection curve.
In the case of a beam bent by transverse loads acting in a plane of symmetry, the bending moment M varies along the length of the beam and we represent the variation of bending moment in B.M diagram. Further, it is assumed that the simple bending theory equation holds good.

If we look at the elastic line or the deflection curve, this is obvious that the curvature at every point is different; hence the slope is different at different points.
To express the deflected shape of the beam in rectangular co-ordinates let us take two axes x and y, x-axis coincide with the original straight axis of the beam and the y - axis shows the deflection.
Further, let us consider an element ds of the deflected beam. At the ends of this element let us construct the normal which intersect at point O denoting the angle between these two normal.
But for the deflected shape of the beam the slope is at any point C is defined,
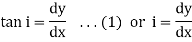
Assuming 
Further 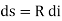
However,
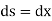 [usually for small curvature]
[usually for small curvature]
Hence 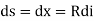
Or
Substituting the value of i, on get
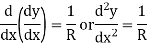
From the simple bending theory
 or
or
So the basic differentials equation governing the deflection of beams is

This is the differential equation of the elastic line for a beam subjected to bending in the plane of symmetry. Its solution y = f(x) defines the shape of the elastic line or the deflection curve as it is frequently called.
The governing differential equation is defined as
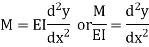
On integrating one get,
 this equation gives the slope of the loaded beam.
this equation gives the slope of the loaded beam.
Integrate once again to get the deflection.
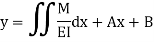
Where A and B are constants of integration to be evaluated from the known conditions of slope and deflections for the particular value of x.
Q3) Derive equation for Cantilever Beam with Concentrated Load at the end.
A3)
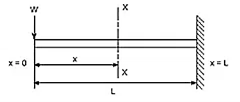
Consider any X-section X-X located at a distance x from the left end or the reference, and write down the expressions for the shear force and the bending moment.
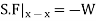
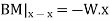
Therefore 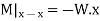
The governing equation 
Substituting the value of M in terms of x then integrating the equation one get

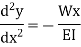
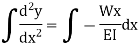
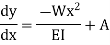
Integrating once more,

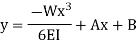
The constants A and B are required to be found out by utilizing the boundary conditions as defined below
i.e at x= L ; y= 0 ——————– (1)
At x = L ;dy/dx = 0 ——————– (2)
Utilizing the second condition, the value of constant A is obtained as
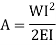
While employing the first condition yields

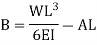

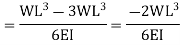
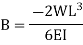
Substituting the values of A and B we get
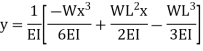
The slope as well as the deflection would be
Maximum at the free end hence putting 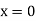 we get,
we get,
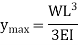
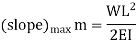
Q4) Derive the equation for Cantilever with Uniformly distributed Loads.
A4)
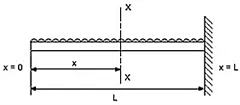
Consider any X-section X-X located at a distance x from the left end or the reference, and write down the expressions for the shear force and the bending moment.
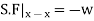



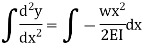
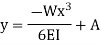
Integrating once more,
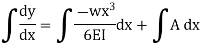
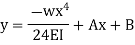
Boundary conditions relevant to the problem are as follows:
1. At x = L; y = 0
2. At x= L; dy/dx = 0
The second boundary conditions yield
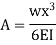
Whereas the first boundary conditions yields
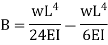

Thus 
So  will be at x=0
will be at x=0


Q5) Derive expression for Simply Supported beam with uniformly distributed Loads.
A5)
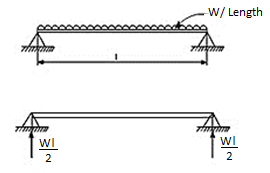
In order to write down the expression for bending moment consider any cross-section at distance of x metre from left end support.
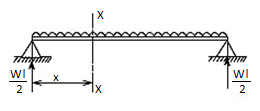
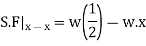
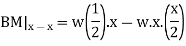
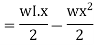
The differential equation which gives the elastic curve for the deflected beam is
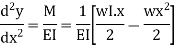


Boundary conditions which are relevant in this case are that the deflection at each support must be zero.
i.e., at x = 0; y = 0: at x = l; y = 0
Let us apply these two boundary conditions on equation (1) because the boundary conditions are on y, this yields B = 0.

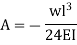
So the equation which gives the deflection curve is

In this case the maximum deflection will occur at the center of the beam where x = L/2 [ i.e., at the position where the load is being applied.] So, if we substitute the value of x = L/2.
Then 

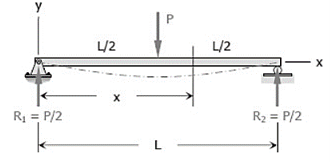
Q6) Determine the maximum deflection δ in a simply supported beam of length L carrying a concentrated load P at midspan.
A6)

At  , therefore,
, therefore, 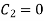
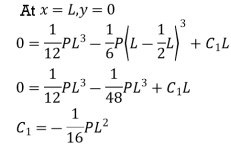
Thus,

Maximum deflection will occur at  (midspan)
(midspan)

The negative sign indicates that the deflection is below the undeformed neutral axis.
Therefore,
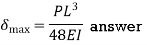
Q7) Determine the maximum value of EIy for the cantilever beam loaded as shown in Fig. Take the origin at the wall.
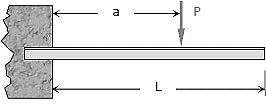
A7)

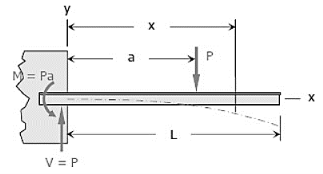
At 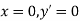 , therefore
, therefore 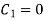
At 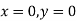 , therefore
, therefore 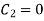
Therefore,

The maximum value of 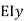 is at
is at  (free end)
(free end)
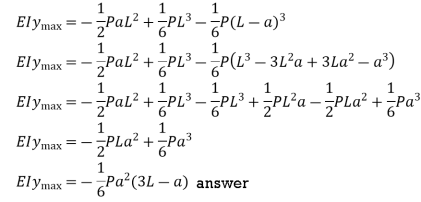
Q8) The simply supported beam shown in Fig. carries a uniform load of intensity wo symmetrically distributed over part of its length. Determine the maximum deflection δ.
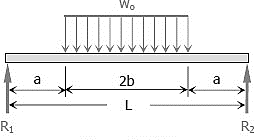
A8)
By symmetry



At 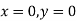 , therefore
, therefore 
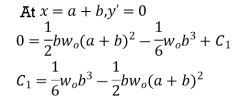
Therefore,
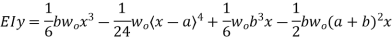
Therefore,
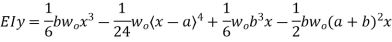
Maximum deflection will occur at 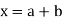 (midspan)
(midspan)

Therefore,
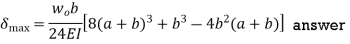
Q9) Compute the value of EI δ at midspan for the beam loaded as shown in fig. If E = 10 GPa, what value of I is required to limit the midspan deflection to 1/360 of the span?
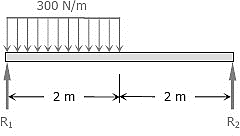
A9)
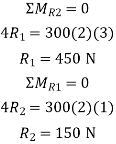

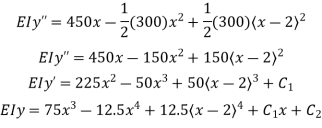 At
At 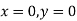 , therefore
, therefore 
At 
 Therefore,
Therefore,
EI 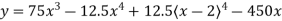
At  (midspan)
(midspan)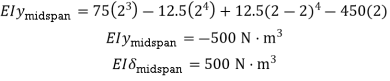 Maximum midspan deflection
Maximum midspan deflection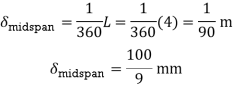 Thus,
Thus,
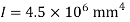 answer
answer
Q10) Compute the midspan value of EI δ for the beam loaded as shown in Fig.
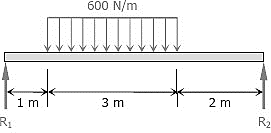
A10)
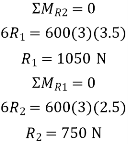


At 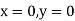 , therefore
, therefore 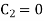

Therefore,
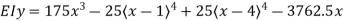
At midspan, 

Thus,
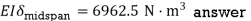
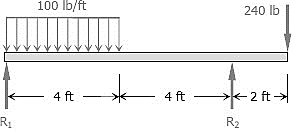
Q11) For the beam loaded as shown in Fig., calculate the slope of the elastic curve over the right support.
A11)


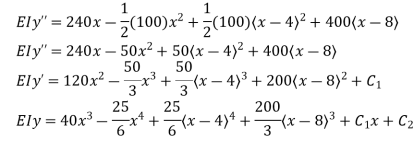
At  , therefore
, therefore 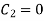
At 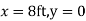
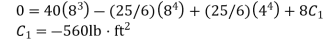
Thus,
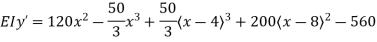
At the right support,