Unit – 5

Axial and hoop stresses in cylinders subjected to

Internal pressure

5.1 Axial and hoop stresses in cylinders subjected to internal pressure

Stress acting along the circumference of thin cylinder will be termed as circumferential stress or hoop stress.

If fluid is stored under pressure inside the cylindrical shell, pressure will be acting vertically upward and downward over the cylindrical wall. Pressure vessel will tend to burst as displayed here in following figure and stresses developed in such failure of cylindrical shell will be termed as circumferential stress or Hoop stress.

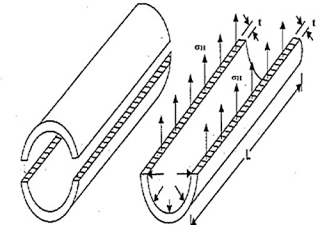
Let us consider here following terms to derive the expression for circumferential stress or Hoop stress developed in the wall of cylindrical shell.

P = Internal fluid pressure

d = Internal diameter of thin cylindrical shell

t = Thickness of the wall of the cylinder

L = Length of the cylindrical shell

σH = Circumferential stress or hoop stress developed in the wall of the cylindrical shell

Cylindrical shell bursting will take place if force due to internal fluid pressure will be more than the resisting force due to circumferential stress or hoop stress developed in the wall of the cylindrical shell.

In order to secure the expression for circumferential stress or hoop stress developed in the wall of the cylindrical shell, we will have to consider the limiting case i.e. force due to internal fluid pressure should be equal to the resisting force due to circumferential stress or hoop stress.

Force due to internal fluid pressure = Internal fluid pressure x Area on which fluid pressure will be acting

Force due to internal fluid pressure = P x (d x L)

Resisting force due to circumferential stress = σH x 2 L t

As we have seen above, we can write following equation as mentioned here.

Force due to internal fluid pressure = Resisting force due to circumferential stress

P x d x L = σH x 2 L t

σH = P x d / (2 t)

σH = P x d/ 2t

Longitudinal (Axial) Stress

For a cylinder closed in both ends the internal pressure creates a force along the axis of the cylinder. The longitudinal stress caused by this force can be calculated as

σL = p d / (4 t)                              

Where

σl = longitudinal stress (MPa, psi)

P = Internal fluid pressure

d = Internal diameter of thin cylindrical shell

t = Thickness of the wall of the cylinder

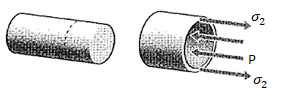
Figure: Free-body diagram for axial stress in a closed-end vessel.

The stresses σz in the axial direction of a cylindrical pressure vessel with closed ends are found using this same approach as seen in Fig. Below, and yielding the same answer:

P (πr2) = σz (2πr) t

σz =pr/2t

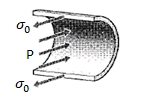
Figure: Hoop stresses in a cylindrical pressure vessel.

However, a different view is needed to obtain the circumferential or “hoop” stresses σθ. Considering an axial section of unit length, the force balance for Fig. Gives 2σθ (t x 1) = p (2r x 1)

σθ =pr/t

Note the hoop stresses are twice the axial stresses. This result different stresses in different directions occurs more often than not in engineering structures, and shows one of the compelling advantages for engineered materials that can be made stronger in one direction than another (the property of anisotropy). If a pressure vessel constructed of conventional isotropic material is made thick enough to keep the hoop stresses below yield, it will be twice as strong as it needs to be in the axial direction. In applications placing a premium on weight this may well be something to avoid.

5.2 Deformation of thick and thin cylinders

Thin Cylinder:

A cylinder or spherical shell is considered to be thin when the metal thickness is small compared to internal diameter. i. e., when the wall thickness, ‘t’ is equal to or less than ‘d/20’, where ‘d’ is the internal diameter of the cylinder or shell, we consider the cylinder or shell to be thin, otherwise thick.

When a thin cylindrical shell is subjected to an internal pressure, there will be an increase in the diameter as well as the length of the shell.

Let, L = Length of the cylindrical shell,

d = Diameter of the cylindrical shell,

t = Thickness of the cylindrical shell,

p = Intensity of internal pressure,

E = Young’s modulus for the material of the cylindrical shell, and

μ = Poisson’s ratio

The increase in diameter of the shell due to an internal pressure is given by:

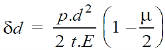
The increase in length of the shell due to an internal pressure is given by:

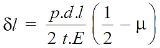
Here, the increase in diameter and length of the shell will also increase its volume.

Therefore, the increase in volume of the shell due to an internal pressure is given by:

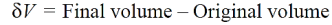
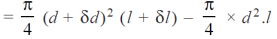
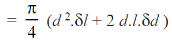  ..(neglecting small quantities) 

Thick Cylinder:

The thickness of the cylinder is large compared to that of thin cylinder. i. e., in case of thick cylinders, the metal thickness ‘t’ is more than ‘d/20’, where ‘d’ is the internal diameter of the cylinder. Magnitude of radial stress (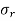) is large and hence it cannot be neglected. The circumferential stress is also not uniform across the cylinder wall. The radial stress is compressive in nature and circumferential and longitudinal stresses are tensile in nature. Radial stress and circumferential stresses are computed by using ‘Lame’s equations.

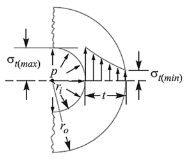
Fig. Thick cylindrical shell        Fig. Tangential stress distribution 

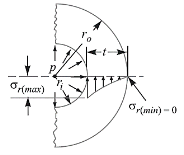
Fig. Radial Stress Distribution

Consider a thick cylinder of having say; 

Let,

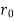= Outer radius of cylindrical shell,

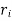= Inner radius of cylindrical shell,

t = Thickness of cylindrical shell =   – ,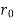

p = Intensity of internal pressure,

μ = Poisson’s ratio,

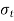= Tangential stress, and

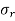= Radial stress

L = Length of the cylinder.

Assuming that the longitudinal fibres of the cylindrical shell are equally strained, According to Lame, the tangential stress at any radius x is given as:

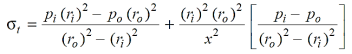
And radial stress at any radius x is given as:

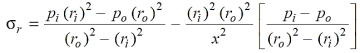
Since we are concerned with the internal pressure ( = p) only, therefore substituting the value

Of external pressure, = 0.

∴ Tangential stress at any radius x,

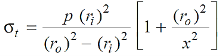  ……..(i)

And Radial stress at any radius x,

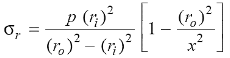……(ii)

As we know that the tangential stress is maximum at the inner surface of the shell (i.e., when (x = 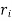) and it is minimum at the outer surface of the shell (i.e., when x = ).

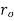Then put the value of x = and x = in equation (i) to obtain maximum tangential stress at the inner surface of the shell,

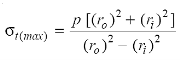
For maximum radial stress at the inner surface of the shell, substituting the value of

x = 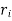and x = 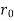in equation (ii),

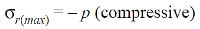
For minimum radial stress at the outer surface of the shell, we get

5.3 Deformation in spherical shells subjected to internal pressure

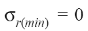
Thin Spherical shell subjected to internal pressure

Consider a thin spherical shell subjected to internal pressure;

Let, V = Storage capacity of the shell,

p = Intensity of internal pressure,

d = Diameter of the shell,

t = Thickness of the shell,

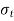= Permissible tensile stress for the shell material.

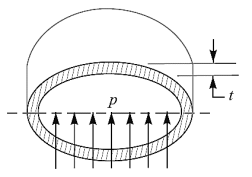
Fig. Thin spherical shell

1. Diameter of the shell:

We know that the storage capacity of the shell,

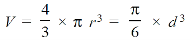
Or

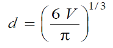
2.     Thickness of the shell:

Force tending to rupture the shell along the centre of the sphere or bursting force;

……..(i)

And Resisting force of the shell is given as;

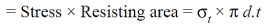…….(ii)

From equating equations (i) and (ii), we have

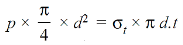
Or,

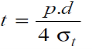
If η is the efficiency of the circumferential joints of the spherical shell, then

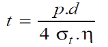
Why is a spherical pressure vessel more efficient than a cylindrical pressure vessel?

Spherical pressure vessels are more efficient with compare to cylindrical pressure vessel. Hence these are widely used for very high-pressure system. (Since there cost of construction is more with comparison to cylindrical pressure vessel. Hence not usually recommended until the pressure is very high.

The reason behind their higher efficiency is the stress distribution. The cylindrical pressure vessel has twice the stresses as generated in spherical system. Hence the thickness obtained in case of spherical pressure vessel for same pressure will be very less with compare to spherical pressure vessel. (nearly half)

Key takeaways

1)     A cylindrical or spherical shell will be considered as thin cylindrical or spherical shell, if the wall thickness of shell is very small as compared to the internal diameter of the shell.

2)     Wall thickness of a thin cylindrical and spherical shell will be equal or less than the 1/20 of the internal diameter of shell

3)     Cylindrical vessel hoop or circumferential stress = σH = P x d/ 2t

4)     Cylindrical vessel Longitudinal stress = σL = p d / (4 t)                              

5)     Thin Spherical hoop stress / longitudinal stress= σφ = σz = pr/2t=pr/2t

References:

1. U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
2. Elements of Strength of Materials (Timoshenko)
3. Strength of Materials (S. Ramamrutham)
4. A Textbook of Strength Of Materials (R K Bansal)
5. Strength of Materials (Dr B.C.Punmia)