Unit - 7

Classification of Curves

Q1) Classify Curves?

A1)

Horizontal curve:

• Definition: The curves which are provided at turning points so as to get gradual change in the direction of alignment of a road or a track are termed as horizontal curves.
• Note that these curves are in the horizontal plan. In railway track, the minimum radius of a horizontal curve should be 175 m for broad gauge.
• Horizontal as well as vertical, curves in case of road must ensure safety, comfort and convenience of the traffic.

Vertical Curve:

• Definition: The curves which are provided in the alignment of road or track at change of gradient is termed as vertical curves.
• Necessity of vertical curves: It gives adequate visibility and safety to the traffic.
• It gives gradual change in grade or slope.
• It gives adequate comfort to the passengers.

Q2) What is Types of Curves & Explain each types Simple curve, Compound curve, Reverse curve & Transition curves?

A2)

Different types of Curves and their applications:

There are four types of horizontal curves:

1. Simple curve
2. Compound curve
3. Reverse curve
4. Transition curve

Simple curve

• The curve which consists of a single arc of a circle of which two straight tangents further connects and brings about a deflection of the road through an angle '0' is called as simple curve. See Fig. For better understanding.
• Simple curve is normally represented by the length of its radius or by the degree of curve.
• This type of curve is provided at every change in alignment of the road or railway à track in a plain and in hilly areas.

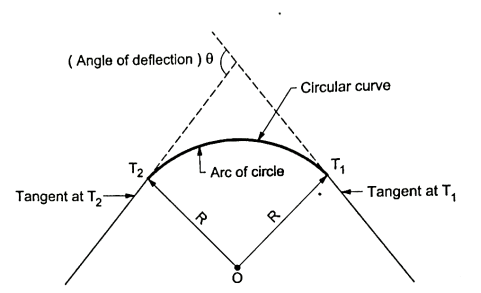
Fig1: Simple curve

Combined curve

• A curve of having the series of two and more simple curves of different radii curving in the same direction is called as compound curves. Refer to the Fig.

For better understanding.

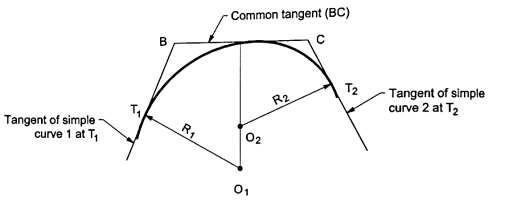
Fig2: Compound curve

• In compound curves, the two adjacent curves will have a common tangent "BC" as shown in Fig.
• The centers of two adjacent curve lie on the same side of the curve as shown in Fig.
• To avoid the cutting through hard rocks, heavy cutting or filling in the alignment of road or track, compound curves are provided.

Reverse curve

• The curve which consists of two simple curves having equal or different radii turning in opposite direction is called as reverse curve. Refer to Fig. 6.4.3 for better understanding.
• The two centres of curves are on opposite sides of a common tangent 'BD'.
• Reverse curves are necessary on hill roads where frequently changes in the direction of travel is required.

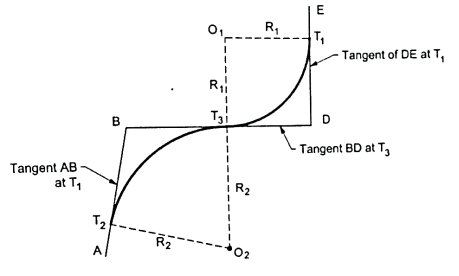
Fig3: Reverse curve

• Reverse curves are also necessary for cross-overs in station yards and in the alignment of the railway tracks in hilly areas.

Advantages of reverse curve:

• This type of curve is often used in the alignment of a hill road.
• It is also used in the layout of railway spur tracks and cross-over.

Disadvantages of reverse curve:

• The use of reverse curve is not suitable on highways where the speeds are high.
• This type of curve is also not suitable in the main railway lines due to high speed.
• There is sudden change of direction in reverse curve and this makes passengers more uncomfortable.
• Steering is dangerous on highways and driver has to be very cautious.

Transition curve:

• The curve in which radius varies gradually from infinity to a finite value equal to that of the circular curve to be connected and vice versa is termed as transition curve.
• These curves are commonly used in railway tracks between the circular curve and a tangent so as to provide easy and gradual change in direction.

There are Two types of vertical curve:

1. Summit Curve
2. Valley Curve

Summit curves:

• Definition: The curves which are having convex surface on upward side is termed as summit curves.
• Vertical curves are used manly when rising gradient intersects a falling grade or when rising gradient meets another rising gradient or when rising gradient meets a horizontal road or when falling gradient meets at a steeper falling gradient. Refer Fig. For better understanding.
• Fig. Shows the different situations where summit curves are provided.

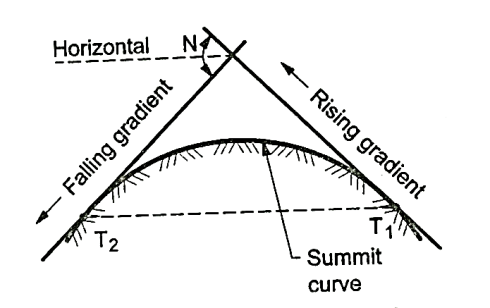
Fig4: A rising gradient intersecting a falling gradient

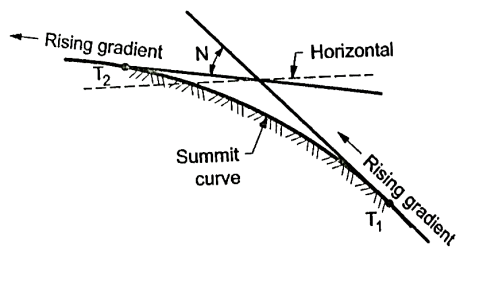
Fig5: A rising gradient meeting another rising gradient

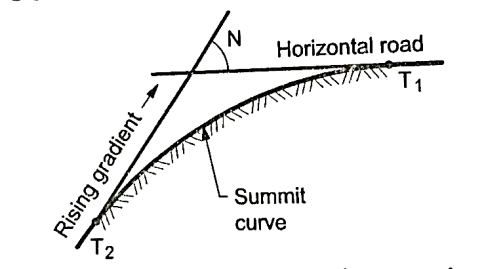
Fig6: A rising gradient meeting at horizontal road

Valley curves:

• Definition: The curves which are having the convex surface on downward side Fig. Shows the different situations where valley curves are termed as valley curve.

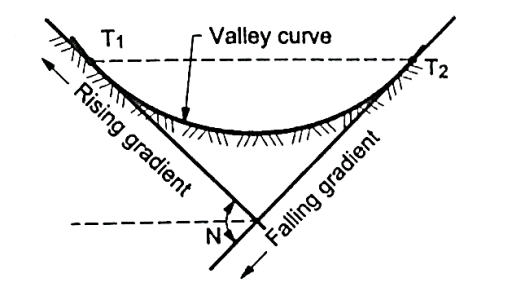
Fig7: A falling gradient intersecting a rising gradient

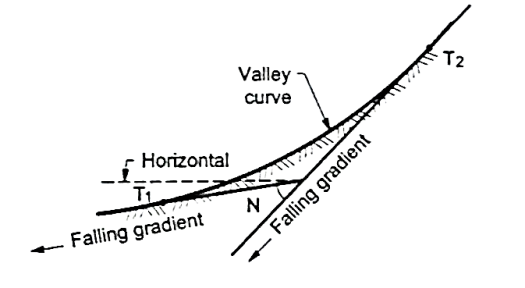
Fig8: A falling gradient meeting another falling gradient

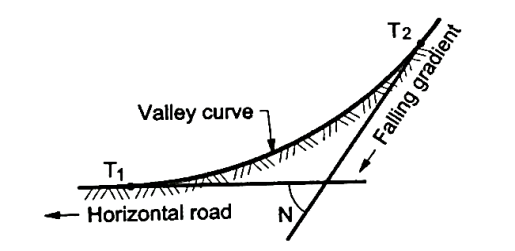
Fig9: A falling gradient meeting a horizontal road

There are Two types of vertical curve:

1. Summit Curve
2. Valley Curve

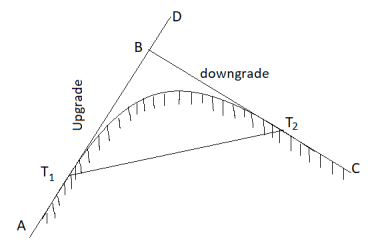
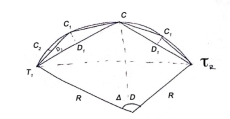
Elements of simple circular curves:

• Refer the Fig. For understanding the various terms of notation for a simple circular curve.

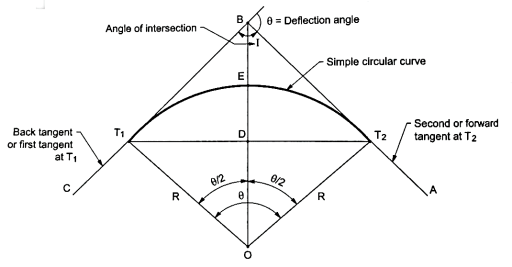
Fig10: Simple circular curve (Right hand curve)

• The common notation which are normally preferred for simple circular curve are as follows:

1. BC and AB are the two tangents drawn to the curve at T1, and T2, respectively. In short, BC and AB are two straight called as tangents.
2. The two tangents AB and BC are intersected at the B which is called as point of intersection. In short, B is the point of intersection of tangents AB and BC.
3. In Fig., the curve deflects to right side. Therefore, it is called as right-hand curve.

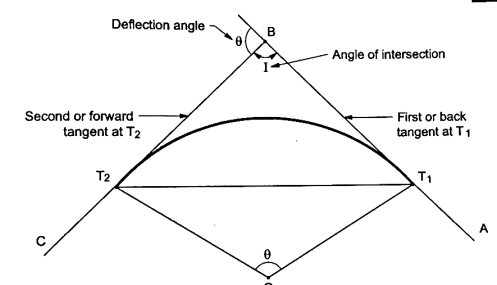
Fig11: Simple circular curve (left hand curve)

4.     In Fig., the curve deflects to left side. Therefore, it is called as left-hand curve.

5.     In Fig., BC is first tangent and also called as back tangent. AB is second tangent and also called as forward tangent. In Fig.AB is first or back tangent at T₁ and BC is second or forward tangent at T₁.

6.     T1, and T2, are the tangent points. T1, shows the starting of the curve and T2, shows the end of the curve.

7.     In fig., I is an angle of intersection and 0 is a deflection angle.

8.     BT1, and B T2, are the lengths of tangent.

9.     T1, T2, is a long chord of length 'L'.

10. The arc 'T1ET2' is a length of curve. 

11. The midpoint 'E' is apex of summit of the curve T1ET2

12. BE is the distance of apex.

13. The angle 'T1OT2' = The deflection angle ''.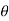

14. DE is a versed sine of the curves.

Q3) What is Methods of layout?

A3)

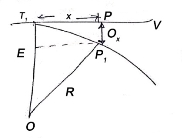
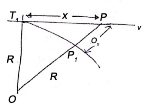
Radial offsets:

• Let Ox=Radial offset PN at any distance x along the tangent

T1P = x

From Δ T1 PO,

PO2 = T1O2+T1 P²

Ox=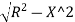 –R   …... (1)

Fig12: setting out by radial offsets

• In order to get an approximate expression for Ox, expand

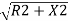
Thus,

Ox=R-R

Neglecting the other terms except the first two, we get

Or Ox=x2/ 2R

When the radius is large

T1P2=PN(2R+PN)

X2=Ox(2R+Ox)

Neglecting Ox in comparison to 2R we get

Ox=x2/2R

Perpendicular offsets:

Fig13: setting out by perpendicular offsets

• Let DN=Ox=offset perpendicular to the tangent

T1D=x=measured along the tangent

Draw NN1 parallel to the tangent

From 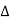leEE1O, we have

E1O2=EO2-E1E2

(R-Ox)2=R2-x2

From which

Ox=R-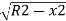

The corresponding approximate expression for Ox may be obtained by expanding the term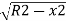. Thus,

Ox=R-R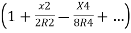

Neglecting the other terms except the first two of the expressions

Ox=R-R+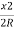

Q4) What is Offsets from chord produced?

A4)

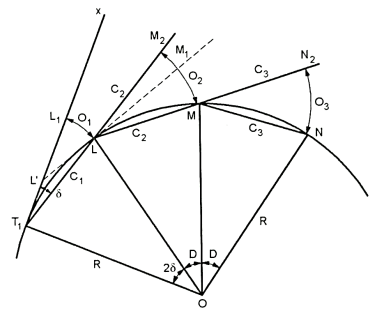
Fig.: setting out the curve by deflection distance

• When the curve is long, this method is useful (generally on highway curves) when a theodolite is not available.

Let T1L1 = T1L =  initial sub-cord= C1

L, M, W are the points on curve

LM = C2, MN = C3etc

T1x = rear tangent

∠ L1T1L = 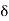= deflection angle of the first chord

L1 L =O1= first offset

M2 M = O2 = second offset

N2 N = O3 = Third offset etc.

Now Arc L1 L = O1 = T1 L 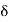    ……(1) 

Since T1x is the tangent to the circle at T₁

∠T O L = 2∠L T L

= 2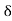

∴ T L = R 2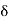

=

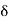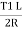
Substituting the value of 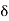in (1) we get

Arc L1 L = O1 = T1L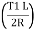

Taking arc T1L=chord T1L (very nearly) we get

O1=C1^2/2R

• Thus, to obtain the value of the second offset O2, for getting the point M on the curve, draw a tangent LM1, to the curve at L to cut the rear tangent in L. Join T1L and prolong it to point M2 such that LM2=LM=C2, length of the second chord.

The O2= M2M

As from equation No. 3, the offsets M1M from the tangent LM1 is given by

L1L =C22 /2R

Angle M2LM1=angle L’LT1 being opposite angles

Again,

Since T1L' and L'L are both tangents, they are equal in length.

Arc M2M1=LM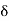2=C2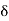

• Generally, the first chord is a sub-chord say of length c, and the intermediate chords are normal chords, say of length C. In that case the above formulae reduce to

O12=C2/2R

O₂ = C/2R(C+C)

03= 04=C/2R(2C)

=C2/R

Q5) Explain Rankine’s Method?

A5)

• Transit theodolite and chain or tape are used in this method.
• Since this method gives more precise results, it is mostly used for setting out the curves in railways and other important work.

Derivation of formula:

• Let R be the radius of the curve and 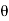be the angle of deflection.
• Refer the Fig. For better understanding and further simplification of derivation.

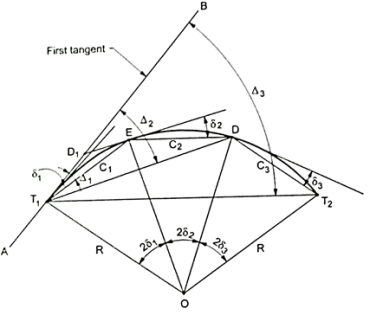
Fig: Rankine’s method of tangential angle or deflection angle

• AB is the first tangent to the curve.
• T1 and T2 are the tangent points.
• E, D, T1, etc. are the successive points on the curve.
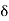• 1, 2, 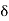3, etc. are the tangential angles or deflection angles made by chords T1E, ED, DT2 etc. w.r.t. Tangents.
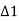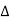• ₁, 2,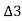, etc. are total tangential angles or deflection angles between:

1. First tangent AB and T1E
2. First tangent AB and ED
3. First tangent AB and DT2, respectively.

• C₁, C₂, C3, etc. are the lengths of chords T1E, ED, DT2, etc. Chord T1E = Arc T1 E assumed to be C

BT1E = 8, =½ T1OE

T1OE = 2,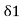

Now,=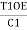

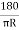
T1OE =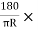C1

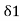2=C1

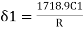minutes

Similarly,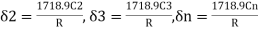

• Total tangential or deflection angles are ,,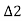, etc. Total deflection angle for first chord

∴

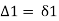
• Total deflection angle 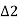, for the second chord ED= BT1D. But BT1D= BT1E+ET1+DET1D is the angle subtended by the chord 'ED' in the opposite segment and hence equal to the tangential angle 'S,' between the tangent at E and chord ED.

Hence,

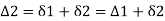
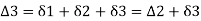
• Check: Total deflection angle (BT1 T2) =

Stepwise procedure for setting the curve by deflection angles:

1. Set up a transit theodolite over the first tangent point "T1, Centering and leveling is done precisely and set the vernier A to 360°.
2. Direct the telescope to A so as to bisect the ranging rod held at B.
3. Set the vernier A to the first deflection angle A, then direct the telescope along T, E.
4. Take one end of the chain or tape at T, and hold the arrow on the chain at a distance equal to the length of first sub-chord. Swing the chain around 'T, and bisect the arrow so as to fix the position on first point E on the curve.
5. Loose the upper plate and set the vernier to the second deflection angle "A". Then direct the line of sight along 'T, D'.
6. Now take the one end of the chain or tape at 'D' and swing the other end. Bisect the arrow, which is already held at the other end. In this way the second point on the chain D is located.
7. In this way, establish points on the curve until the end of the curve i.e., T₂: The slight deflection can be adjusted on the last few pegs.

• Note that if error goes beyond the permissible limit, whole procedure should be checked or repeated.
• Note that in left hand curve, each of the calculated values of the deflection angles A, A, etc. should be minus from 360°. In this way, the angles obtained will be set on the vernier of theodolite for setting out the curve. Enter the reading in following field note.

Q6) What is Transition Curve?

A6)

The curve in which radius varies gradually from infinity to a finite value equal to that of the circular curve to be connected and vice versa is termed as transition curve.

• These curves are commonly used in railway tracks between the circular curve and tangent so as to S provide easy and gradual change in direction.

Necessity:

1. To provide gradual change in the radius of curvature.
2. To provide smooth entry of vehicle from a straight portion to curved portion.
3. To permit gradual application of the super elevation and extra widening at horizontal curves.
4. To provide safety to the vehicular traffic.

Types of Transition Curve:

The types of the transition curve which are in common use are:

1. A Cubic parabola
2. A clothoid or spiral
3. A lemniscates

Type of vertical curve

i)                   Upgrade followed by a downgrade

Fig

Ii)                 Upgrade followed by another upgrade

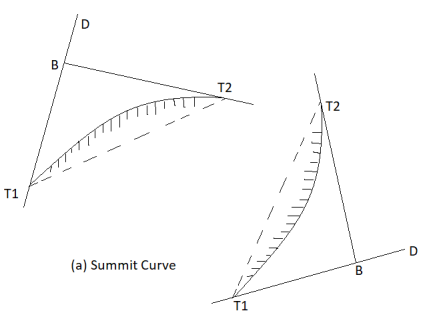
Fig 20

Iii)              A downgrade followed by an upgrade

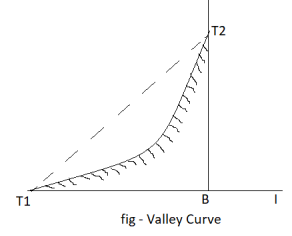
Fig21

Iv)               A downgrade followed by another downgrade

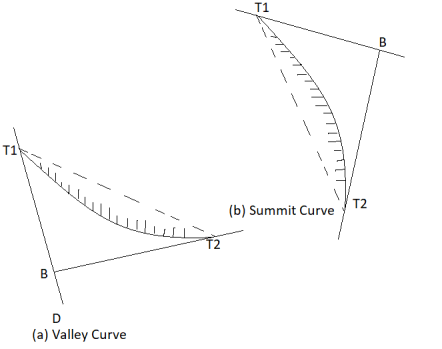
Q7) What is Super-elevation?

A8)

Super elevation in roads is largely furnished at the horizontally curved part of the roads wherein the outer fringe of the street pavement is raised with admire to the internal edge, therefore imparting a transverse slope at some point of the period of the horizontal curve of the street.

Super elevation at the horizontal curve is one of the maximum crucial functions within side the creation of the roads. It could be very important to offer super elevation in roads for the secure motion of cars at the curved part of the roads. It allows the fast-shifting cars to securely by skip via the curved part of the roads with stability.

The inward transverse inclination that is supplied to the cross-segment of the pavement of street on the horizontally curved part of the roads is referred to as super elevation. Super elevation is likewise referred to as Cant or Banking. Super elevation in roads is essentially supplied at the horizontally curved part of the roads wherein the outer fringe of the street pavement is raised with admire to the internal edge, for this reason presenting a transverse slope at some stage in the period of the horizontal curve of the street. This transverse inclination to the floor of the street pavement is referred to as Super elevation.

Purpose of Providing Super elevation in Roads • The predominant goal of supplying super elevation is to counteract the impact of centrifugal pressure performing at the shifting vehicle. • To save you the dangerous impact at the floor of the roads because of incorrect distribution of load at the roads.

To assist the fast-shifting automobiles to by skip thru a curved route without overturning or skidding. • To lessen the upkeep value of the street at the curved portion. • To make sure the clean and secure motion of automobiles and passengers at the curved part of the roads. Super elevation is expressed because the top of the outer fringe of the pavement with appreciate to the width of the pavement.

Super elevation or Cant:

It is defined as the raising of outer end of a road or outer rail over inner one.

h = super elevation = e

w = weight of vehicle

P = centrifugal force

g = acceleration due to gravity

R = radius of curve

G = gauge distance between rails

u = speed of vehicle

B = width of pavement

= Angle of super elevation

h = super elevation = e

w = weight of vehicle

P = centrifugal force

g = acceleration due to gravity

R = radius of curve

G = gauge distance between rails

u = speed of vehicle

B = width of pavement

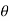= Angle of super elevation

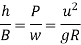
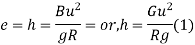
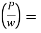Centrifugal ratio

Q8) What is Length of transition curve?

A9)

Length of transition curve: -

a)     Method of arbitrary gradient: -

e = total super elevation provided at junction of transition curve with circular curve

L = ne

Where rate of super elevation is ∆ in n

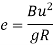
(b) Method of Time rate: -

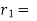time rate of super elevation

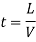
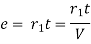
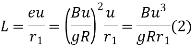
Method of rate of change of radial acceleration

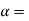Rate of change of radial acceleration

t is the time attained by radial acceleration (a)

a =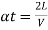

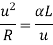
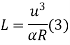
Q9) What are the Characteristics of a transition curve?

A10)

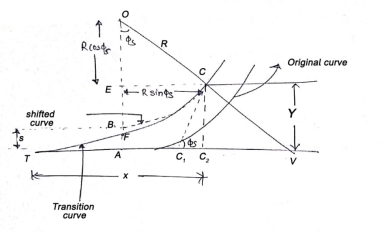
Characteristics of a transition curve:

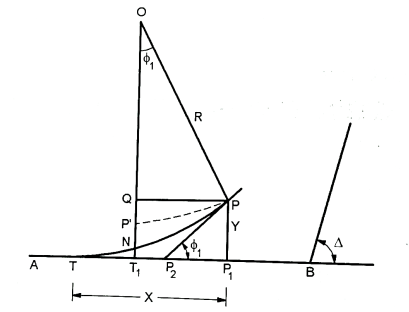
Fig14: Transition curve

Let TB = the original tangent

T= the starting of the transition curve

P= the end of the transition curve

PP₂= the tangent to both the transition and circular curve at P

Y = PP1=the offset to junction point (P) of both curves.

X = TP1=the x coordinate of P

PP’= the redundant circular curve

T₁ = the point of intersection of the line OP’ perpendicular to the tangent to the circular curve at P and original tangent AB.

S=ET1= the shift of the circular curve

N =the point in which OP’ cuts the transition curve

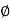₁ = the spiral angle between the common tangent PP2and the original TB

R = the radius of the circular curve (OP)

L = the length of the transition curve

1) Now PP’=R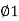

But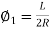

∴PP’=R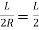

Since PN is very nearly equal to PP’

∴EN =

i.e., the shift (PT1) bisects the transition curve at N

Hence TN =1/2

2) Draw PG perpendicular to OP’

Now, S = P’T₁=GT₁-GP’

= PP’-GE’

S = Y-R (1-cos )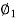

Or S=Y-2Rsin2

But Y=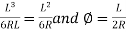

S=Y-2Rsin2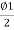

=Y-2R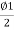

2R sin² S=Y-2R sin

=Y-2R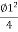

=

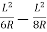
S=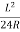

Also, NT1 =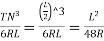

NT₁ =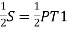

i.e., the transition curve bisects the shift.

(3) Total tangent length (BT):

(a) True Spiral

BT = BT1+T1T

Now T1T=TP1-P1T1

=TP1-PG

=X-Rsin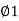

OT1= OP' + P'T1

= R+S

BT1=(R+S) tan

Where 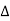is the deflection angle between the straights.

∴BT = (R+S) tan+ (X-R sin)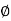

Now,

X=L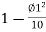 and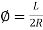

∴BT=(R+S) tan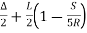

Q10) Explain Equation of transition curves?

A11)

Equations of various transition curves:

Elements of the Clothoid:

The centrifugal force acting on a vehicle is given by

P=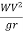

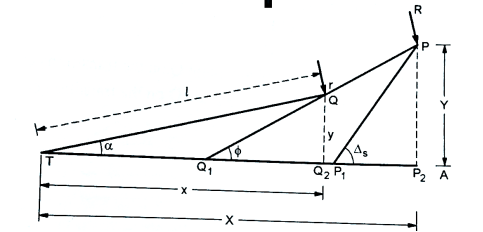
Fig15

Where,

r-is the radius of curvature at any point on the curve

If the centrifugal force P is to increase at a constant rate, P must vary with time

Also, if the speed of the vehicle is constant, the distance I along the transition curve measured from the tangent point must vary with time.

Hence, we have

P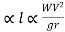

But W1V and g are all constants

Hence l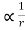   …… (1)

Lr=constant=LR

Thus, the fundamental requirement of a transition curve is that its radius of the curvature at any point shall vary inversely as the distance (l) from the beginning of the curve. Such a curve is the clothoid curve is also known as the ideal transition curve.

Let

T= tangent point = beginning of the transition curve

TA= initial tangent

P= point of junction of the transition circular curve

Q = any point on the curve at distance I along the curve.

r = radius of the curve at any point Q.

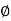= the inclination of the tangent to the transition curve at Q to the initial

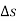= spiral angle = the angle between the initial tangent and the tangent to the transition curve at the junction point E

l= length of the curve from T to B

R= radius of the circular curve

X = the x coordinate of P

Y = the y coordinate of P

= TQ₂ = x coordinate of any point Q on the transitions curve

Y = OQ2= y coordinate to any point Q on the transition curve.

We have,

Lr = LR=Constant

Or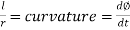

Integrating both side

We get

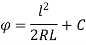
When l=0,

∴C=0

Hence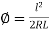

This is the intrinsic equation of the ideal transition curve.

Equation can also be expressed as

l =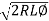

1 = K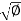

Where

k =

When L=l,

Elements of a Cubic Parabola Curve:

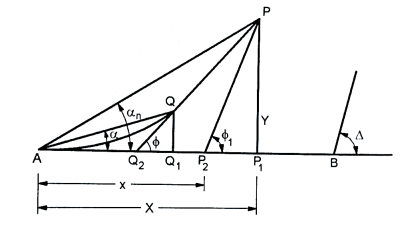
Fig16: Cubic parabola curve

Let x = AQ₁ = The distance of any point Q on the tangent AB from the commencement A of the curve.

y = Q, Q=the perpendicular offset to the point Q.

I= the length of the transition curve AQ

X = AP, the distance of the junction point P on transition curve with the circular curve from A measured along AB.

Y = PP the Perpendicular offset to the junction point P

L= the length of the transition curve.

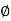= QQ2B= the angle between the tangent line AB and the tangent to the transition curve at any point Q.

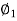= PP2B= the angle between AB and the tangent at P (Spiral angle)

R= the radius of the circular curve

= ∠QAB = the deflection angle to any point Q.

a = ∠PAB = the deflection angle to the junction P

y =

Now, tan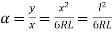

From the intrinsic equation,

∴

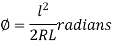
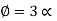…. (2)

=

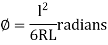
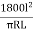=minutes   …. (3)

Since l=L,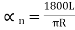… (4)

=

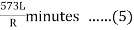
If the degree (D) of the curve be given instead of radius, the corresponding values of

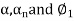may be found by substituting the value of R in terms of D,viz in equation 3 & 5.

Hence, 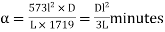…. (6)

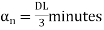…. (7)

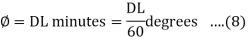
From equation (1), the Co-ordinates of P are

X = Land Y=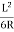 = four times the shift

Total tangent length = BA= (R+ Stan)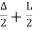

In which

S= the shift and

= the deflection angle between the two tangent S.

These are curves in a vertical plane, used to join two intersecting grade lines.

A vertical summit curve is provided when a rising grade join a falling grade and a vertical curve is provided when a falling grade joins a rising grade.

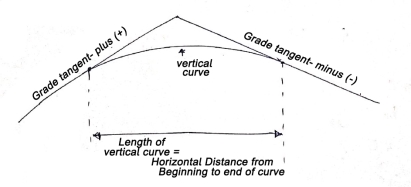
Fig17: Vertical curve

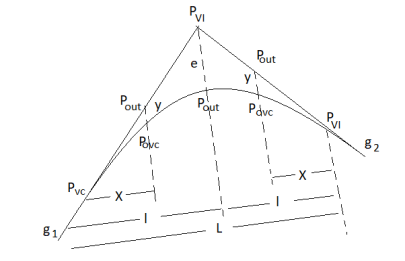
Fig18

PVC – point of vertical curvature place where curve begins

PVT – point of vertical tangency, where curve end.

PVI – point of vertical intersection, where grade tangents intersect.

POVC - point on vertical curve applies to any point on parabola

POVT - point on vertical tangent, applies to any point on other tangent

are grade tangent at PVC and PVT respectively.

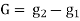
(a)  Length of vertical curve

L = algebraic difference of two grades/ rate of change of grade

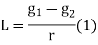
(b)  Change of end of curve

PVT = change of intersection point + half the length

Q11) What is Shift?

A12)

The distance thru which the curve is shifted is referred to as shift (S) of the curve, and is identical to, wherein L is the duration of every transition curve and R is the radius of the preferred round curve (EFE'). The duration of shift (T1E1) and the transition curve (TE) collectively bisect every other.

The distance AB thru which the primary round curve is shifted inwards to deal with the transition curve is known as shift (s) or throw. The distance among the unique centre O and the shifted centre O' is normally small.

Q12) What is Tangent length?

A13)

a) Total Tangent Length

Tangent length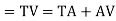

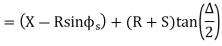
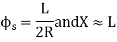
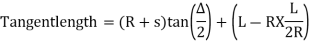
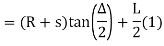
(b) Length of long chord

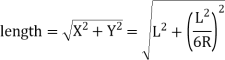
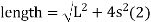
(c) Total length of curve

Total length of curve

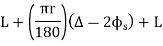
=Total length        (3)

(d) Apex distance E

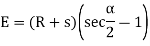
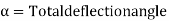
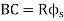
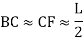
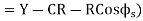
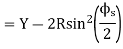
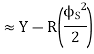
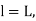
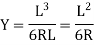
Q13) What is Curve length of combined curve?

A14)

Curves are normal bends furnished within side the traces of communiqué like roads, railways etc. and additionally in canals to result in the sluggish extrade of course. They also are used within side the vertical aircraft in any respect adjustments of grade to keep away from the abrupt extrade of grade on the apex. Curves furnished within side the horizontal aircraft to have the sluggish extrade in course are referred to as Horizontal curves, while the ones furnished within side the vertical aircraft to attain the sluggish extrade in grade are referred to as vertical curves. Curves are laid out at the floor alongside the centre line of the work. They can be round or parabolic.

Assume or calculate the i) duration of the transition curve. (ii) discover the cost of the shift train, . (iii) Locate the tangent factors T and T as in article (11.15,) (iv) Calculate the offset for the transition curve as in article (11.14 xiv) (v) Locate die factors at the transition curve in addition to at the round curves with the aid of using starting off the respective offsets.

Q14) Two straights intersect at a chainage of 2610 m, the deflection angle being 36 A circular curve of 400 m radius is to be set. Calculate the chainages of the tangent point of right-handed circular curve. Peg interval is 30 m.

A15)

Given: Deflection angle (0) = 36°.

BT₁ Tangent length = R tan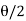=400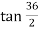 129.967 =129.97 m

= (4+9.97) chains

Length of curve =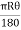= =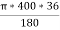251.327=251.33m

= (8+11.33) chains

Chainage of the second tangent point "T1':

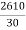=-(4+9.97) chains

= (87) -(4+9.97) chains

= (83+9.97) chains

Chainage of the second tangent point ‘T2':

= (Chainage of T,) + (length of curve)

= (83 +9.97) + (8 +11.33)

= (91 +21.3) chains

Q15) Two roads meet at an angle of 150. Calculate the data necessary for setting out curve of 10 chains radius to connect the two straight roads if it intended to set out curve by chain and offset from long chord, chain used is a 30 m chain only. Calculate two offsets from centre of long chord.

A16)

Given:

I =point of intersection

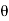=deflection angle = 180° - 150° = 30°

R = radius of curve = 10 chains = 10x30=300 m (since 30 m chain used)

Length of long chord (L) =2 R sin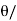2

L = 2x300 x sin 30°/2 = 155.29 m

Note: Length of long chord is taken in round figures as 160 m.

∴L = 160 m

Ordinate at the middle of the long chord (O)= versed sine

O0 = R-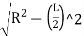

=300-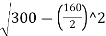

O0=300-289.136

∴O0=10.86 m

The various ordinates can be calculated by the following formula as,

Ox=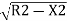 –(R-O0)

Consider the offset at 20 m from the centre.

O20=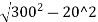-(300-10.86)

=299.33-289.14=10.19 m

(It is the first offset from the centre of long chord)

O40=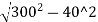-(300-10.86)

=297.32-289.14=8.18m

(It is the second offset from the centre of long chord.)

Hence the two offsets from the center of long chord are 10.19 m and 8.18 m.

Extension of problem:

Remaining offsets till curve ends can be calculated as follows:

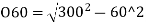-(300-10.86)

=293.938-289.14

=4.8 m

O80=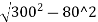-(300-10.86)

=289.136-289.14

=0 m

Q16) What is Setting out of simple and transition curve?

A17)

(a)  Linear method

(i)    Offset from long chord

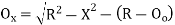
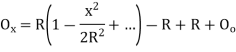
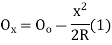
Where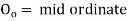

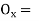offset at some point P at distance x from midpoint D.

(ii) Perpendicular offset from tangent

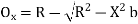
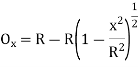
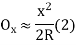
(iii) Radial offset from tangent:

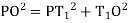
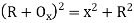
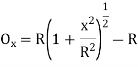
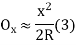
(iv) Successive Bisection of Arc or chord

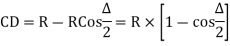
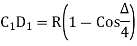
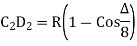
(v) By offset from chord produced

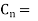last sub chord

b) Angular method

i) Rankine's method of deflection angle

- It is generally used for setting out a circular curve of long length and large radius.

- It gives good result except then chords are long as compared to radius, so that variation between length of an Arc and its cord becomes considerable.

- It is used in highway and Railway

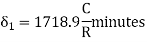
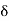= Tangential angle

C = chord length

(ii) Tachometric method

-It is similar to Rankine’s method of deflection angle.

- The theodolite at 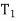may be used as Tacheometric and Tacheometric observation are made.

- Less accurate as compared to Rankins.

- Chaining is completely dispersed in this method.

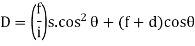
(For Incline and line of sight)

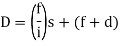
(For horizontal line of sight)

v)                 Two theodolite method

-         Convenient than any of to our method when ground is undulating rough and not suitable for Linear measurements.

-         Two theodolites are used and linear measurement are completely eliminated.

-         Hence, most accurate method.

-         It is based on principle that angle between the tangent and chord is equal to angle subtended by chord in opposite segment.

-         Time consuming method

-         Most accurate method

-         Highly expensive.