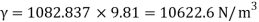Unit - 1

Basic Concepts and Definition

Q1) Explain distinction between fluid and solid?

A1)

• We have a common, vague idea of ​​difference. Solid is not easily damaged; and the liquid is easily deformed (we can easily move through the air).
• Although it is quite descriptive, this unusual view of the difference between solids and liquids is not very satisfying from a scientific or engineering point of view.
• The obvious difference is based on bow items that are disabled under the action of the external load.
• Fluid is defined as a substance that progressively deforms when subjected to shear stress of any size.
• The shear pressure (force at the per unit area) is created whenever the tangential force is applied to the surface as shown to the individual.
• When solid foods such as iron or other metals are subjected to shear pressure, they will initially be disabled (usually the smallest factor), but they will not continue to degenerate (flow).
• However, common liquids such as water, oil, and air satisfy the definition of liquid — that is, they will flow when they are made by shear pressure.
• Some materials, such as slurries‚ tar, putty, toothpaste, etc., are not easily separated because they will behave stronger if the shear pressure applied is less, but if the pressure exceeds a certain critical amount, the object will move.
• The study of such materials is called Rheology and does not fall into the category of classical fluid mechanics.
• Although the formation of fluid cells is important in the separation of fluids from one another, due to the large number of molecules involved, it is impossible to study the behavior of individual molecules when attempting to explain the function of a liquid at rest or on the move.
• Instead, we demonstrate this behavior by considering the scale, or macroscopic. The amount of interest rate, when the ratio is tested over a small volume containing a large number of molecules.

Q2) Explain density, Specific weight?

A2)

• Quantity (precisely, the size of the volume of a volume; also known as a specific weight), of an object whose weight is the volume of the unit.
• The symbol most commonly used for congestion is ρ (the capital letter of the Greek word rho), although the Latin letter D may also be used. Statistically, quantity is defined as the quantity divided by volume

ρ = m/ v

• Where ρ size, m size, and V is volume. In some cases (for example, in the United States oil and gas industry), overcrowding is freely defined as its weight per unit volume, although this is scientifically incorrect - this number is specifically called a specific weight.

• Pure material overcrowding has the same value as its mass concentration.
• Different materials tend to have different strengths, and congestion can be accompanied by durability, purity and packaging.
• Osmium and iridium are the most well-known substances in normal temperature and pressure conditions.

• To facilitate quantitative comparisons in various unit systems, sometimes incorporating an empty value "related size" or "specific gravity", e.g. A measure of the quantity of an object in that of a normal object, usually water. So the relative density of less than one relative in water means that the object is floating in water.

• The quantity of matter varies with temperature and pressure. These variations are usually small in solids and liquids but very large in gases. Increasing the pressure on an object reduces the volume of the object and thus increases its size.
• Increasing the temperature of an object (with a few exceptions) reduces its size by increasing its volume. In many cases, heating the bottom of the liquid leads to a temperature rise from the bottom to the top, resulting in a decrease in the volume of this warm liquid. This causes it to rise in relation to dense non-heated objects.

• The multiplication of quantities of matter is sometimes called its specific volume, which is a term sometimes used in thermodynamics. Quantity is a powerful structure in that the increase in the number of objects does not increase its size; instead it increases its weight.

Measurement of density

• There are many strategies and levels to measure the size of the materials used. Such techniques include the use of a hydrometer (fluid rehydration method), Hydrostatic balance (fluid and firmness method), an immersive body system (beverage fluid method), pycno meter (fluid and solids), air comparisons pycno meter (solid), oscillating densitometer (liquid), and pour and tap (solid).
• However, each method or procedure measures different types of quantities (e.g. Density, bone size, etc.), so it is necessary to understand the type of density measured and the type of object in question.

Homogeneous material

• The plurality of all the points of an object corresponding to its equality and its magnitude is divided by its total volume. Weight is usually measured in scale or balance; volume can be measured directly (from the geometry of an object) or by liquid transfer. To determine the size of the liquid or gas, hydrometer, dasy meter or Cororiol is flow meter can be used, respectively. Similarly, a hydrostatic weight uses water migration due to the immersed material to determine the size of the object.

Heterogeneous material

• When the body is incompatible, its homosexuality varies between different regions of the object. In that case the congestion around any given area is determined by the calculation of the maximum volume around that area. At the lowest volume limit the density of the non-point object

m = integration v ρ (r)d V

Non compacted material

• In practice, bulk materials such as sugar, sand, or ice contain voids. Many substances exist in nature such as flakes, pellets, or granules.

• Voids are regions that contain something other than imaginary objects. Normally this void is air, but can also contain vacuum, liquid, solid, or a different gas or gas mixture.

• Bulk volume - including an empty fraction - is usually obtained by simple measurement (e g by measuring cup measurement) or by geometry from known sizes.

• Mass divided by the volume of the pile determines the congestion of the pile. This is not the same as volumetric mass.

• To determine the size of the weight of the volume, one must first reduce the volume of the missing portion. Sometimes this can be determined by geometric thinking. Close packaging for equal parts of the empty fraction can be at least 74%.
• It can also be determined by force. Some materials in bulk, however, like sand, have a flexible fraction that depends on how the material is moved or poured. It may be loose or compact, with more or less air space depending on the handling.

• In practice, an empty fraction is not just air, or gas. In the case of sand, it could be water, which would be useful to measure as the empty fraction of sand filled with water - once all the air bubbles have been removed - can be much more flexible than dry sand compared to empty air.

• In the case of non-composite materials, one should also be careful in determining the size of the material sample.
• If the material is under pressure (the frequency of bad air on the surface of the earth) the determination of the weight from the measured sample scale may need to respond to the effects of the stiffness due to the quantity of the empty material, depending on how the measurement is made.
• In the case of dry sand, sand is so thicker than air that the softening effect is often overlooked (less than one thousandth).

• Mass conversion when removing one empty object and another while maintaining a constant volume can be used to measure the empty fraction, if the difference in the size of the two empty objects is reliably known.

SPECIFIC WEIGHT

• A specific weight, also known as a unit weight, is the unit weight of an item.
• The most commonly used value of the Earth's water table is 4 ° C, which is 9.807 k N / m3 or 62.43
• Gravity words, and very unusual weights, are used for relative size. A common symbol of a certain weight is γ, the Greek letter Gamma.

Definition

• The specific weight, γ, of a story is defined as the product of its plurality, ρ, and the common gravitational force, g: Gamma = ρ g
• Quantity of matter is defined as quantity by unit volume, typically measured in kg / m3. Gravity is usually faster due to gravity, usually given in m / s2, and on Earth it is generally considered to be 9.81 m / s2.
• Unlike quantity, a certain weight is not a fixed asset. Depending on the speed of gravity, it varies from place to place. Pressure can also affect values, depending on the bulk modulus of the object, but often, at moderate pressure, it has a less significant effect than other factors.

Q3) Explain specific gravity?

A3)

• The relative quantity or gravitational force is a measure of the size (volume of a unit volume) of an object in the quantity of a given object.
• The gravitational force of the liquid is almost always measured in relation to the water obtained (at 4 ° C or 39.2 ° F); for gases, the reference is air at room temperature (20 ° C or 68 ° F). The term "relative congestion" is often popular in scientific practice.

• If the density of an object is less than 1 it means that it is more dense than the reference; if it is greater than 1 then it is thicker than the reference.
• If the relative size is 1 exactly the stiffness is equal; that is, equal amounts of these two objects have the same weight. If the reference is water, then an object with a relative mass (or certain gravitational force) less than 1 will float in the water.
• For example, an ice cube, with a relative weight of about 0.91, floats. An object with a relative weight greater than 1 will sink.

• Temperature and pressure should be specified on both the sample and the reference. The pressure is approximately 1 atm (101.325 kPa). When not, it is very common to specify the exact size. Sample and reference temperatures vary from industry to industry.
• In British brewing practice, gravity, as described above, increased by 1000. Certain gravity is widely used in the industry as an easy way to obtain information about the complexity of solutions for various substances such as brines, sugar solutions (syrups, juices, honeys, brewers wort, must, etc.) and acids.

Uses

• The quantity associated with it can help to measure the maturity of a liquid or a gas, or determine the density of an unknown substance from a known congestion in another. Related quantities are often used by geologists and mineralogists to help determine the mineral content of a rock or other sample.
• Gemologists use it as an aid in the identification of gemstones. Water is preferred as a reference because measurements are easy to make in the field (see below for examples of measuring methods).

• As the basic application of industrial quantity measurements in the industry the determination of the focus of objects is a powerful solution and this finding in the RD vs concentration tables is very important for the analyst to enter the table in the correct way for the related quantities.
• For example, in the brewing industry, the Plato table, which calculates the concentration of sucrose in large quantities against real RD, initially (20 ° C / 4 ° C) based on the weight estimates of sucrose solutions made at laboratory temperatures (20 ° C) but with reference to positioning of water at 4 ° C very close to temperatures where the water has its maximum H (H) magnitude 2O) equal to 0.999972 g / cm3 (or 62.43 lb · ft - 3).
• The ASBC table used today in North America, when based on Plato's original table is the apparent average size of (20 ° C / 20 ° C) on the IPTS-68 scale where the water level is 0.9982071 g / cm3. In sugar, soft drinks, honey, fruit juice and sucrose-related industries the mass extraction is taken from this SG-using activity (17.5 ° C / 17.5 ° C). As a final example, British RD units are based on a reference temperature with a sample of 60 ° F and thus (15.56 ° C / 15.56 ° C).

Q4) Explain kinematic and dynamic viscosity?

A4)

Dynamic Viscosity

Absolute viscosity - the coefficient of total viscosity - is the measure of internal resistance. Dynamic (absolute) viscosity is the tangential force at each unit area required to move one horizontal plane in relation to another plane - by unit velocity - while maintaining unit distance outside the fluid.

Shave pressure between layers of fluid in straight lines can be defined by Newtonian fluid as

Liquid - viscosity and velocity profile

Fig no 1 Dynamic and kinematic viscosity

Shear depression can be shown

τ = μ dc / d y

   = μγ.                                  ........   (1)

Where

τ = cutting pressure on liquid (N / m2)

μ = strong viscosity of liquid (N s / m2)

d c = unit velocity (m / s)

d y = unit distance between layers (m)

γ = dc / d y = shear rate (s-1)

Equation (1) is known as the Newtons Law of Friction.

(1) Can be rearranged to reflect Dynamic viscosity as

μ = τ dy / dc

      = τ / γ.                                     .......... . (1b)

• In the SI system the dynamic viscosity units are N s / m2, Pa s or kg / (m s) - where

1 Pa s = 1 N s / m2 = 1 kg / (m s) = 0.67197 lbm / (ft s) = 0.67197 slug / (ft s) = 0.02089 lbf s / ft2

• Strong viscosity can also be expressed in the metric CGS system (centimeter-gram-second) such as g / (cm s), dyne s / cm2 or poise (p) where

1 poise = 1 dyne s / cm2 = 1 g / (cm s) = 1/10 Pa s = 1/10 N s / m2

• Effective use Poise is usually very large and the unit is therefore divided by 100 - into a small centipoise (cP) unit - where

1 P = 100 cP

1 cP = 0.01 poise = 0.01 gram per cm second = 0.001 second Pascal = 1 milliPascal second = 0.001 N s / m2

20.2oC (68.4oF) liquids have a perfect viscosity of one - 1 –centiPoise.

Kinematic Viscosity

Kinematic viscosity is a measure of the total viscosity - (or intensity) of a quantity - the amount of non-energy. Kinematic viscosity can be obtained by dividing the total viscosity of the liquid by the amount of fluid mass

ν = μ / ρ                               .................. (2)

Where

ν = kinematic viscosity (m2 / s)

μ = full or strong viscosity (N s / m2)

ρ   = density (kg / m3)

In the SI-system the unit of kinematic viscosity theory is m2 / s - or the most commonly used Stoke (St) where

• 1 St (Stokes) = 10-4 m2 / s = 1 cm2 / s

Stoke comes from the CGS unit program (Centimeter Gram Second Second).

As the Stoke unit is usually divided by 100 into smaller units centi Stoke (c St) - there

• 1 St = 100 c St

• 1 c St (centi Stoke) = 10-6 m2 / s = 1 mm2 / s

• 1 m2 / s = 106 centi Stokes

The gravitational force of 20.2oC (68.4oF) is almost the same, and the kinematic viscosity of 20.2oC (68.4oF) water is designed to operate 1.0 mm2 / s (c Stokes). The most precise water viscosity at 20.2oC (68.4oF) is 1.0038 mm2 / s (c St).

Conversion from full viscosity to kinematic in Imperial units can be shown as

ν = 6.7197 10-4 μ / γ.                           .................... (2a)

Where

ν = kinematic viscosity (ft2 / s)

μ = full or strong viscosity (c P)

γ = specific weight (lb / ft3)

Q5) Explain variation of viscosity with temperature?

A5)

• The viscosity of the fluid is due to two contributing factors, namely the interaction between fluid molecules and the transfer of pressure between molecules. In the case of gases the penetration between molecules is large and therefore the interaction of molecules is small.
• But in terms of liquid the molecules are very close together and as a result there is a great deal of interaction. Thus in liquids, viscosity is mainly due to the interaction of the middle cells, while in gases the viscosity is mainly due to the transfer of molecular pressure.
• The bonding force of the molecule decreases with increasing temperature and therefore with increasing temperature the viscosity of the liquid decreases.

The following formula provided by Poiseuille shows the dependence of the viscosity of the liquid on the heat-

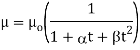
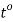Where, Viscosity of the liquid at C in poise

Viscosity of the liquid at C in poise

 and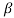 are constant characteristics of the liquid.

For water,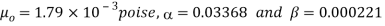

• In the case of gases, as mentioned earlier, the combination of molecules can be ignored viscosity depends largely on the transfer of molecular pressure on the right side to the direction of motion. As the temperature increases the movement of the cells increases that is, there will be a greater transfer of pressure and therefore the viscosity increases. Holman gave the following statement on gas viscosity-
• 

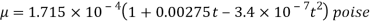
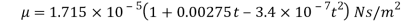
Viscosity of Liquids

Liquid	Viscosity at various temperatures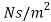
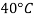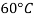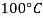Water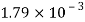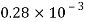
Alcohol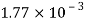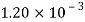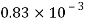
Kerosene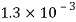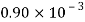
Petrol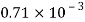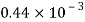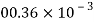

Viscosity of Air at various Temperature

Temperature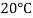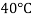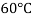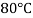
Viscosity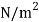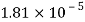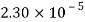

Q6) Explain Newton’s law of viscosity and vapor pressure?

A6)

Newton's viscosity law states that the shear pressure between adjacent water layers is equal to the velocity gradients between these two layers.

The shear pressure ratio and shear ratio are constant, at a given temperature and pressure, and are defined as viscosity or coefficient of viscosity.

Newton’s Law of viscosity,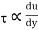

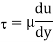
Where,

Viscosity

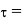Shear stress=F/A

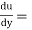Rate of shear deformation

Vapour Pressure

• Vapor pressure (or vapor pressure in British English; see spelling difference) or equilibrium moisture pressure is defined as the pressure exerted by the smoke on the thermodynamic equilibrium and its thick (solid or liquid) phases at a given temperature in a closed system.
• Equilibrium pressure is an indicator of evaporation rate. It is related to the tendency of particles to leak into a liquid (or solid). An object with a high vapor pressure at normal temperatures is often called an invariant.
• The pressure exerted by evaporation over a liquid is known as vapor pressure. As the temperature of a liquid increases, the kinetic energy of its molecules also increases.
• As the kinetic energy of the molecules increases, the number of molecules that evaporates also increases, thus increasing the vapor pressure.

Fig no 2 Vapour pressure

• The vapor pressure of any substance increases with the temperature according to Clausius- Clapeyron's relationship. The atmospheric pressure of boiling liquid (also known as the normal boiling point) is the temperature at which the pressure of the vapor is equal to the atmospheric pressure of the atmosphere.
• With the increasing temperature of that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and to raise the liquid to form vapor bubbles inside the object.
• The formation of a deep bubble in a liquid requires a high temperature due to the high pressure of the liquid, because the pressure of the liquid rises above the atmospheric pressure as the depth increases.
• The most important thing at the deepest depth is the high temperature needed to start bubble formation. The friction of the surface of the bubble wall leads to excessive pressure on very small, initial bubbles.
• The vapor pressure that one part contributes to total pressure in the system is called incomplete pressure. For example, sea air, and filled with water vapor at 20 ° C, has incomplete water pressures of about 2.3 k Pa, 78 k Pa of nitrogen, 21 k Pa of oxygen and 0.9 k Pa of argon, a total of -102.2 k Pa, which forms the basis of the normal atmospheric pressure.

Measurement and uses

• Vapor pressure is measured in standard pressure units. The International System of Units (SI) recognizes pressure as a unit derived from the magnitude of energy in each area and defines pascal (Pa) as its standard unit. One pascal is a newton per square meter (N · m - 2 or kg · m - 1 · s - 2).
• The pulse pressure test measurement is a simple procedure for normal pressures of between 1 and 200 k Pa. The most accurate results are found near the boiling point of objects and large errors result in smaller doses than 1kPa.
• Procedures usually include cleaning the test object, separating it from the container, removing any foreign gas, and then measuring the equilibrium pressure of the gas phase of the object in the container at various temperatures.
• Better accuracy is achieved when care is taken to ensure that everything and its vapor are at a set temperature. This is usually done, such as using an isotonic scope, by inserting the contents of the liquid in a liquid bathtub.
• Very low vapor pressure of solids can be measured using the Knudsen cell method
• According to medical conditions, vapor pressure is sometimes expressed in other units, especially millimeters of mercury (mmHg). This is important for flexible anesthetics, most of which are body fluids, but with very high vapor pressure.

Q7) Explain boiling point and cavitation?

A7)

Boiling Point

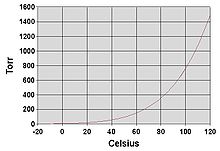
Fig no 3 Boiling point

• The boiling point of a liquid varies depending upon the surrounding environmental pressure. A liquid in a partial vacuum has a lower boiling point than when that liquid is at atmospheric pressure.
• A liquid at high pressure has a higher boiling point than when that liquid is at atmospheric pressure. For example, water boils at 100 °C (212 °F) at sea level, but at 93.4 °C (200.1 °F) at 1,905 meter (6,250 ft) altitude. For a given pressure, different liquids will boil at different temperatures.
• The normal boiling point (also called the atmospheric boiling point or the atmospheric pressure boiling point) of a liquid is the special case in which the vapor pressure of the liquid equals the defined atmospheric pressure at sea level, one atmosphere.
• At that temperature, the vapor pressure of the liquid becomes sufficient to overcome atmospheric pressure and allow bubbles of vapor to form inside the bulk of the liquid. The standard boiling point has been defined by IUPAC since 1982 as the temperature at which boiling occurs under a pressure of one bar.

• The heat of vaporization is the energy required to transform a given quantity (a mol, kg, pound, etc.) of a substance from a liquid into a gas at a given pressure (often atmospheric pressure).

• Liquids may change to a vapor at temperatures below their boiling points through the process of evaporation. Evaporation is a surface phenomenon in which molecules located near the liquid's edge, not contained by enough liquid pressure on that side, escape into the surroundings as vapor.
• On the other hand, boiling is a process in which molecules anywhere in the liquid escape, resulting in the formation of vapor bubbles within the liquid.

• Like all liquids, water evaporates when its vapor pressure reaches its surrounding pressure. Naturally, atmospheric pressure is low at high altitudes and water boils burn low. The boiling water temperature of atmospheric pressure can be compared to the Antoine equation:

Log 10 (P/ 1 Torr) = 8.07131 -[( 1730.63 °c) / (233.426° c + Tb)]

• Or transportation into this temperature explicit form

Tb = [1730.63 °c/ (8.07131 - log 10(P/ 1 Torr))] - 233

Where the temperature Tb is the boiling point in degree Celsius and the pressure P is in Torr

Relation between the normal boiling point and the vapour pressure of liquid

Fig no 4 Log linear Vapour pressure chart

• The steam pressure chart on the right contains graphs of vapor pressure relative to the temperature of the various beverages. As can be seen from the chart, beverages with very high vapor pressure have very low boiling points.
• For example, at any given temperature, methyl chloride has the highest pressure of any gut in the liquid on the chart. It also has the lowest boiling point (-24.2 ° C), at which point the methyl chloride pressure curve (blue line) crosses the horizontal pressure line of one atmosphere of absolute vapor pressure.
• The critical point of the liquid is the very high temperature (and pressure) that it will boil.

Cavitation

• Cavitation is a process in which a decrease in pressure to or under pressure from a liquid vapor leads to the formation of vapor-filled pores in the liquid. When placed under high pressure, these gaps, called "bubbles" or "voids", collapse and can create shocking waves that can damage equipment. These shock waves are strong when they are very close to the inserted bubble, but they quickly become weak as they spread away from the insert

• Cavitation is an important cause of wear in some engineering situations. The collapse of the voids entering near the metal causes cyclic stress through repeated implosion. This causes excess fatigue of the metal which causes a type of wear also called "cavitation". The most common examples of this type of wearable pumping equipment, and bending where there is a sudden change in the flow of fluid. Cavitation is usually divided into two behavioral categories: inertial (or temporal) cavitation and non-inertial cavitation.

• The process by which a void or bubble in a liquid falls rapidly, producing a shock wave, is called an inertial cavitation. Inertial cavitation occurs naturally in strikes of shrimp and pistol shrimps, as well as plant tissue. In man-made objects, it is possible for control valves, pumps, propellers and power inserts.

• Non-inertial cavitation is a process in which a bubble in a fluid is forced to change in size or shape due to some form of energy input, such as an acoustic field. Such cavitation is commonly used in ultrasonic cleaning facilities and can also be seen in pumps, propellers, etc.

• Since shock waves formed by collapsing spaces are strong enough to cause significant damage to parts, cavitation is often undesirable to machinery (although desirable when used intentionally, for example, sterilizing contaminated surgical instruments, dissecting contaminants in water purification systems, emulsify tissue cataract surgery or lithotripsy of kidney stones, or homogenize fluids). Special protection is often avoided in the construction of turbines or propellers, and eliminating cavitation is a major field in the study of fluid dynamics. However, sometimes it helps and does not cause damage when the bubbles fall away from the equipment, such as at high altitudes.

• Cavitation can occur when the local pressure in a liquid reaches a level below the pressure of the liquid vapor at the actual temperature. According to the Bernoulli Equation this can happen if the fluid accelerates to a control valve or to a pump-in area.

• Vaporization itself does not cause damage - damage occurs when the vapor almost immediately after evaporation decreases when the velocity decreases and the pressure increases.

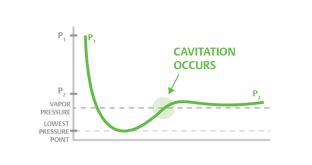
Fig no 5 Cavitation

Avoiding Cavitation

Cavitation can be generally avoided

• Increase the distance (pressure difference) between the actual static pressure on the liquid - and the pressure of the liquid vapor at direct temperature

This can be done by:

• Regenerative engineering components that initiate high speeds and low static pressures
• To increase the total or local pressure in the system
• To reduce the temperature of the liquid

Redesign Components Launch High Speed ​​and Low Static Pressure

Walking and injury can be avoided by using special equipment designed for extreme conditions.

• Situations with large pressure drops can be handled by Multi Stage Control Valves
• Challenging pump conditions with fluid temperatures near vaporization temperature can be treated with special pumps - performance behind other conditions than centrifugal pumps

Increasing total or local pressure in the system

• By increasing the total or local pressure in the system the distance between stationary pressure and vaporization pressure increases and vaporization and cavitation can be avoided.
• The balance between stationary pressure and vaporization pressure - an indication of possible vaporization, is often expressed by Cavitation Number.
• Unfortunately it is not always possible to increase the total static pressure due to system configuration or other limitations. Local static pressure in some parts can increase by lowering (rising) part of the system. Control pipes and pumps should usually be placed at the lowest point of the system to raise the immovable head.
• This is a common solution for boiler feed pumps that receive hot condensate (water up to 100 °C) from condensate receivers in steam plants.

Q8) Explain surface tension?

A8)

• Surface tension is the tendency for the liquid to shrink into the smallest possible area. Facial friction allows insects (e.g. Water arrows), to float and slide on the surface of water without immersion.
• Where fluids combine with air, the resulting incompatibility arises from the greater attraction of liquid molecules to each other (due to bonding) than to air molecules (due to adhesion).
• There are two main processes in play. One is the internal energy of the extra molecules that make the liquid enter. The second is the gravitational force associated with the surface of the membrane. The effect of the net is that the liquid behaves as if its surface was covered with a thick membrane.
• Due to the high attraction of water molecules to each other through the hydrogen bond web, water with a surface elevation (72.8 millinewtons (mN) per meter at 20 ° C) than most other beverages. Facial incompatibility is an important factor in the case of capillarity.
• Extra tension is a measure of the strength in the length of each unit, or the strength in the area of ​​each unit. This is similar, but when referring to the energy in each unit area, it is common to use the term energy energy, which is a common term in the sense that it also applies to solids.
• In science fiction, ground tension is applied either to the pressure of the earth or to higher forces.

Causes

• Due to the relative strength the molecule is pulled evenly on all sides by neighboring chemical molecules, resulting in zero energy. The upper molecules do not have the same molecules on all sides so they are pulled inwards. This creates some internal pressure and forces wet areas to penetrate that small area.
• There is also a surface tension in the liquid-air optical connector that will withstand external forces, due to the interaction of water molecules.
• The gravitational force that works between molecules of the same type is called cohesive force and those that work between molecules of different types are called cohesive forces.
• The balance between fluid mixing and its adhesion to the contents of the container determines the water level, contact angle and position of the meniscus. When cohesion dominates (preferably, the adhesion capacity is less than half the cohesive force) the moisture is low and the meniscus pulls against a straight wall (with respect to mercury in a glass container).
• On the other hand, when adhesion controls (the holding capacity of more than half of the cohesive force) the moisture is high and the same meniscus is concave (as in water in a glass).
• Facial tension is the result of the formation of water droplets. Although easily deformed, water droplets tend to be drawn in an unequal circular motion on the overlapping forces of the upper layer. In the absence of additional energy, droplets of almost all liquid may be round. The rounded shape reduces the "wall friction" required by the upper layer according to Laplace law.
• Another way to look at surface tension is power. A molecule that communicates with a neighbor is in a lower state of energy than it is alone.
• Internal molecules have as many neighbors as possible, but boundary molecules are lost in the neighborhood (compared to internal molecules) and therefore have higher potency.
• In order for a liquid to reduce its energy level, the number of molecules at higher energy limits must be reduced. A reduced number of boundary molecules leads to a much lower surface area.
• As a result of the reduction in area, the area will take on the potential smoothness (statistical evidence that the "smooth" formation reduces the surface area depending on the use of the Euler-Lagrange figure). Since any curvature of the impact shape results in a larger area, there will be higher strength.

Effect of surface tension

Water

Many of the effects of global conflict can be seen in ordinary water:

• Beads of rain water on the surface of the wax, like a leaf. Water adheres weakly to melt and solidify itself, so water collections become droplets. Extra tension gives them their intimate circular shape, because the field has the smallest area over the volume size.

Fig no 6 Water bending on leaf

• The formation of droplets occurs when the weight of the liquid is increased. Flushing (below) indicates that water is attached to the mains for maximum gain until it is extended to an area where ground height can no longer keep the pump connected to the tap. After that it separates and the surface tension creates a partial reduction. When a stream of water flowed out of a tap, the river broke in pieces when it fell. Gravity lightens the stream, and the moisture of the earth drains you into the fields.

Fig no 7 Water dripping from a tap

• The movement of thick objects in water occurs when an object is not soft and its weight is small enough to be carried by forces from the earth's crust. For example, water abusers use ground tension to move on the surface of a lake in the following way. The dehydration of the water rider's leg means that there is no attraction between the leg molecules and the water molecules, so when the leg moves down into the water, the surface tension of the water tries to restore its softness to its flexibility due to the leg. This water behavior pushes the water rider up so that you can stand on the water as long as its weight is small enough for the water to support it. The surface of the water acts like an expanding film: the feet of the insect cause cracks in the surface of the water, increase the surface area and the tendency to decrease the earth's curv (such surface) water pushes the insect's feet upwards.

Fig no 8 Water striders stay atop the liquid because of surface tension

• The separation of oil and water (in this case, water and liquid wax) is caused by a facial imbalance between different drinks. This type of ground tension is called "interface tension", but its chemistry is the same.

Fig no 9 Lava lamp

• Tears of wine the formation of drops and streams along a glass containing an alcoholic beverage. The reason for this is the complex interaction between the different surface tension of water and ethanol; a combination of water-soluble changes by ethanol and ethanol evaporates faster than water.

Fig no 10 Tears of wine

Surfactants

Surface tension is seen in other common causes, especially when surfactants are used to reduce it:

• Soap bubbles have very large areas with very small size. The foam in the clear water is unstable. The addition of surfactants, however, can have a stabilizing effect on bubbles (see Marangoni effect). Note that surfactants actually reduce water resistance by a factor of three or more.
• Emulsions are a type of colloid in which the surface of the earth plays a role. Smaller pieces of oil suspended in pure water will automatically merge into larger masses. But the presence of the surfactant provides a decrease in surface tension, which allows for the stabilization of the minute droplets of oil in most liquids (or vice versa).

Q9) Explain capillarity?

A9)

• Capillary action (sometimes capillarity, capillary motion, capillary effect, or wicking) is the ability of fluid to flow in small areas without assistance, or even to counteract external forces such as gravity.
• The effect can be seen in the formation of fluid between the hairs of the paint brush, in a thin tube, in the smooth material such as paper and cement, in other non-abrasive materials such as sand and carbon fiber, or organic cell.
• It occurs due to intermolecular forces between liquids and solid surrounding environments. If the diameter of the tube is small enough, then a combination of ground incompatibility (caused by coagulation within the liquid) and the ability to adhere between the wall of the liquid and the vessel to form a liquid.
• The first recorded view of the capillary act was by Leonardo da Vinci. A former Galileo student, NiccoloAggiunti, was said to be investigating the carrying of the wheels.
• By 1660, capillary action was still a novelty for Irish chemist Robert Boyle, when he reported that "some Frenchmen wanted to know" realized that when the capillary tube was submerged in water, the water would rise "up into the Pipeline". Boyle then reported on a trial in which he put a capillary tube in red wine and then inserted a tube.
• You have found that the vacuum has no visible effect on the rise of the fluid in the capillary, so the performance of the fluid in the capillary tubes is due to a specific condition different from that which controls the barometers baro meters.
• Some quickly followed Boyle's lead. Some (e.g., HonoreFabri, Jacob Bernoulli) thought that fluid was rising in the capillaries because air could not enter the capillaries as easily as fluid, so air pressure was lower within the capillaries.
• Some (e.g., Isaac Vossius, Giovanni Alfonso Borelli, Louis Carre, Francis Hauksbee, Josia Weitbrecht) thought that liquid particles were attracted to each other and capillary walls.
• Although experimental studies continued through the 18th century, effective treatment of capillary values ​​up to 1805 by two researchers: Thomas Young of the United Kingdom [16] and Pierre-Simon Laplace of France.
• They found the equivalent of the Young - Laplace capillary act. By 1830, German mathematician Carl Friedrich Gauss had determined the parameters of the capillary (i.e., conditions on a solid visual connection). Known as Kelvin's equation.
• German philosopher Franz Ernst Neumann (1798-1895) subsequently decided to collaborate between two non-alcoholic beverages.
• Albert Einstein's first paper, sent to Annalen der Physik in 1900, was astonishing.
• Capillary penetration into media sources shares its powerful equipment through the flow of empty tubes, as both processes are opposed by viscous force.
• As a result, the most common tools used to demonstrate this practice are capillary tube. When the lower end of the glass tube is immersed in fluid, such as water, the concave meniscus forms.
• Adhesion occurs between the fluid and the solid inner wall that pulls the liquid column until there is a sufficient amount of gravity force to overcome these intermolecular forces.
• The length of the contact (edge) between the top of the liquid column and the tube is equal to the width of the intestine, and the weight of the liquid column is equal to the square area of ​​the tube.
• Therefore, a narrow tube will pull the liquid column farther away from the broad bone, provided that the internal water molecules interact sufficiently with the outer ones.

Q10) Explain bulk modulus of elasticity and compressibility?

A10) An elastic modulus (also known as a modulus of elasticity) is a value that measures an object or object to the object of a highly deformed object (i.e., non-permanent) in which pressure is applied. The expandable modulus of the material is defined as the slope of the pressure point in the region of the elastic deformation: Solid material will have a very high modulus. The elastic modulus has the following form:

Delta = stress / strain

Where the pressure is the force that causes the change to be divided by the area in which the force and gravity are used is the rate of change of a particular parameter caused by the distortion in the actual parameter value. Since the difficulty is flawless, the delta will be the same as the units of pressure.

Determining how pressure and complexity will be measured, including indicators, allows for many types of expandable model to be defined. The three main ones are:

1. The Young (E) modulus defines a solid, or tilt, inclination of an object along the axis when opposing forces are used on that axis; defined as a measure of the severity of the stiffness of the stiffness. It is often referred to as the elastic modulus.
2. The shear modulus or stiffness modulus the second parameter of Lame) defines the tendency of an object to shave (change in shape with a fixed volume) when operated by opposing forces; is defined as the shear pressure above the shear type. The shear modulus is part of the viscosity detection.
3. The modulus in the plural (K) defines volumetric stiffness, or the tendency of an object to deform in all indicators when loaded equally in all indicators; is defined as the volumetric pressure over the volumetric mass, and the opposite of the pressure. Modulus in bulk extension of Young's modulus has been in three dimensions.

• Two other extensible methods are Lames first parameter, λ, and P-wave modulus, M, as used in the modulus comparison table given below.

• Homogeneous and isotropic substances (the same in all directions) (solids) have their own (linear) stretchy properties that are fully defined by two stretchable conditions, and one can choose any pair. Given the expansive module, all other expandable methods can be calculated according to the formulas in the table at the bottom of the page.
• Liquids are special because they cannot support shear stress, which means the shear modulus remains zero. This also means that Young's modulus of this group remains a point.

• In some texts, the modulus of elasticity is called constant elastic, and most sizes are called modulus elastic.

COMPRESSIBILITY

• Compression is an asset to be reduced to a minimum by pressure. This material is the result of porosity, and the change in mass occurs from particles that come close together by pressure.
• Liquid pressure is actually a measure of the change in the quantity that will be produced in a liquid by a certain change. Gases, in general, are highly compressed and most liquids have very low pressures.
• The fact that the effects of stress can have a profound effect on the flow of fluid. The study of this flow when changes in quantity and temperature are most important is what is known as compressible flow fluid or gas dynamics.

Q11) Density of liquid is 850 kg/m³. Determine relative density and weight density of the liquid. With reason state whether the liquid will float on water or not

A11)

Gives:

p= 850kg/m'.

P. 1000kg/m (standard value)

To find: Relative density, weight density

Relative density

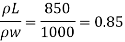
Weight density

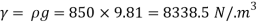
The liquid will float on water because weight density of liquid is less than water.

Q12) On a certain planet a correctly calibrated spring balance shows the weight of a body s 12 N, the mass of which is 4.893 kg. Find the value of gravity on this planet.

A12)

Given:

Weight W= 12 N.

Mass m = 4.893 kg

Weight = Mass x acceleration

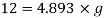
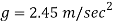
Acceleration due to gravity on a certain planet is 2.45 m/sec.

Q13) What is the specific volume of material with specific gravity 0.87?

A13)

Given:

Specific gravity=0.5,

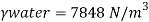
To find: Specific volume.

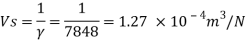
Q14) The specific volume of a certain gas is 0.7m/kg Determine its specific weight and mass density.

A14)

Given:

Specific volume =0.7

To find: Mass density, specific weight

Mass density (p)

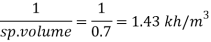
Specific weight (Y)

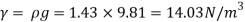
Q15) Calculate the specific weight, density, specific volume and relative duty of oil which 7 N per liter.

A15)

Given:

Weight W=7N,

Volume V= 1 litre = 10^-3 'm^3

To find:

Specific weight,

Specific volume,

Relative density

Specific weight Y

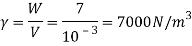
Density

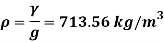
Specific volume (Vs)

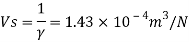
Relative density

Q16) 2 liter of petrol weighs 14N. Calculate the specific weight, density, specific volume and specific gravity of petrol with respect to water.

A16)

Given: V=2 liter = 2 x 10-3m,

W=14N

To find:

1. Specific weight,
2. Density,
3. Specific volume
4. Specific gravity.

1. Specific weight

Specific weight = Mass density x Acceleration due to gravity

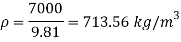
2.     Specific volume (V)

3.     Specific gravity (S)

Q17) A 400 ml of certain liquid weight 9N calculate the weight density and specific gravity of the liquid.

A17)

Given:

Volume V= 400 ml-0.4 L=0.4/1000=4x10^-4 m^3

Weight W=9N

To find: Weight density, specific gravity

1. Weight density (Y) =

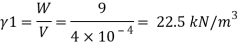
2.     Specific gravity

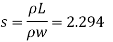
Q18) A plate 0.02 mm distance from a fixed plate, moves at 60 cmvs and requires a force of 3 N/m² to maintain this speed. Determine the fluid viscosity between the plates.

A18)

Given: Distance between plates

Dy= 0.02 mm = 0.02 x 10-3 m

Velocity of upper plate u 60 cm/s 0.6 m/s

Change in velocity du=u-0-0.6 m/s.

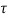= Force per unit Area = 3 N/m²

To find: Viscosity

Using Newton's law of viscosity

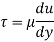
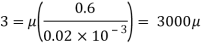
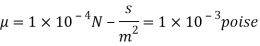
The fluid viscosity between the plates is 1 x 10-3 poise,

Q19) A flat plate of area 2.5 x 10 mm² is pulled with a speed of 0.4m's relative to another plate locate at a distance of 0.15mm from it. Find the force and power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise

A19)

Given:

A=2.5 x 10 mm²=2.5m²,

Du= 0.4m/s dy-0.15mm = 0.15 x 10 m,

=1 poise = 0.1N-s/m

To find: Force, power

Using Newton's law of viscosity:

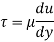
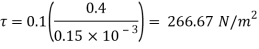
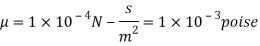
As we known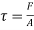

Power required to move the plate at speed 0.4 m/s

= Force x Velocity = 666.67 x 0.4 N-m/

1 N-m/s = 1 Watt

P = 266.67 Watt

Power required moving the plate is 266.67 Watt.

Q20) The space between two square flat parallel plates is filled with oil. Each side of the plate is 720 mm. The thickness of the oil film is 15 mm. The upper plate, which moves at 3 ms requires a force of 120 N to maintain the speed. May 2016. 6 Marks

Determine:

(1) The dynamic viscosity of oil.

(2) The kinematic viscosity of oil if the specific gravity of oil is 0.95

A20)

Square plate of side, a = 720 mm=0.72 m

Thickness of oil film, t = 15 mm= 15 x 10

Velocity of plate v= du= 3m/s

Force F= 120 N

Specific gravity s= 0.95

To find

Mass density,

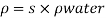
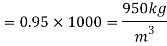
Area of plate,

A= 0.72x0.72 = 0. 5184 m²

Using Newton's law viscosity

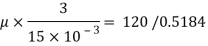
Dynamic viscosity 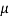= 1.157 N/m²

Kinematic viscosity, v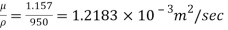

Q21) A body with gravity force of 500 N with a flat surface area 0.2 m slides down a lubricated inclined plane making a 30° angle with the horizontal. For viscosity of 0.1 kg s/m and body speed of 1 m/s. Determine the lubricant film thickness

A21)

Given:

Area A = 0.2 m²

Weight of late W = 500 N

Velocity of plate u = 1 m/sec 0.1kg /m²=0.1 x 9.81 N.s/m² = 0.981 N-s/m²

To find: Thickness of film.

Component of W along the plate W sin 8= 500 sin 30= 250 N

Shear force on the bottom surface of the plate

F = 250N

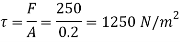
The lubricant film thickness is 0.785 mm

Q22) A rectangular plate 1.2 m x 0.4 m. Weighting 970N slides down a 45° inclined surface at a uniform velocity of 2.25 m/s. If the 2mm gap between the plate and the inclined surface is filled with oil, determine the viscosity of oil.

A22)

Given:

Area A = 12x04 0.48 m²

Weight of plate W =970 N

Velocity of plate u = 2.25 m/sec

Thickness of film t = dy = 2 mm = 2 x 10³ m

To find: Viscosity

Component of W along the plate= W sin

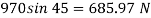
Shear force on the bottom surface of the plate

F= 685.89 N

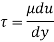
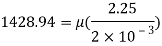
The viscosity of the liquid is 12.7 poise.

Q23) A skater weighing 1000 N attains a speed of 72 km/hour on ice, average skating area being 10 cm². The dynamic coefficient of friction between the Skater and ice may be taken as 0.015. Determine the average thickness of water. Layer existing between the skater and the skating surface. Viscosity of water at 0°C may be taken 1 x 10 N-s/m².

A23)

Given:

W=1000N,

u = 72 kmph = 72x=20m/sec,

A = 10 cm² = 10 x 10 m², -0.015, 10¹N-s/m²

To find: Average thickness.

Force responsible for motion = Frictional resistance

F = μN=pW

Where N= W

F= 0.015 x 1000 = 15 N

Newton's law of viscosity

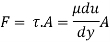
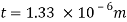
Average thickness of water layer is 1.33 x 10 m

Q24) A body weighing 1000 N slides down at a uniform speed of 1 m/s along a lubricated Inclined plane making 30° angle with the horizontal. The viscosity of lubricant is 0.1 kg/ms and contact area of the body is 0.25 m². Determine the lubricant thickness assuming linear velocity distribution. -June 2011. 6 Marks

A24)

Given:

W= 1000 N,

= 30°

Du = V = 1m/s,

A=0.25 m²

H=0.1 kgm/s 0.1x9.81 Nm/s = 0.981 Nm/s

To find: Lubricant thickness t

Shear force= Weight component along plane

= 1000 sin 30

F = 500 N

Shear stress

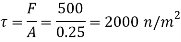
By Newton's law of viscosity

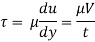
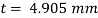
The lubricant thickness is 4.905 mm.

Q25) Calculate the gauge pressure and the absolute pressure within:

(1) a droplet of water 0.3 cm in diameter

(2) a jet of water 0.3 cm in diameter.

Assume the surface tension of water as 0.07 N/m and atmospheric pressure as 101.3 N/m² Dec. 2010, 4 Marks

A25)

Given:

d = 3mm = 3 x 10³ m.

 water = 0.073N/m.

Patm = 101.3 N/m² atm

For droplet and air bubble

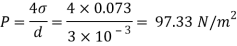
Absolute pressure. (P) = Pgauge + Patm = 97.33 + 101.3 = 198.63 N/m²

For jet

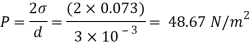
Absolute pressure in jet

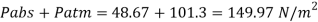
Q26) Determine the diameter of a droplet of water in mm it t pressure inside is to be greater than that outside by 13 Nm². Take a 7.26 10 Nm.

A26)

Given:

P-130 N/m²

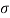= 7.26×10^-2 N/m

For droplet, P

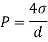
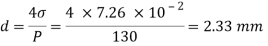
The diameter of a droplet of water is 2.33 mm

Q27) In the surface tension at air water interface is 0.070 Nm what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?

A27)

Given: -

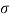= 0.07 Nm.

D= 001mm= 0.01 = 10 m

An air bubble has only one surface,

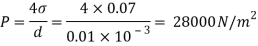
The pressure difference between inside and outside of an air bubble is P= 25000N/m2

Q28) Calculate the pressure inside a soap bubble of 50mm diameter. Take surface tension at the soap air interface as 0.1Nm

A28)

Given:

= 0.1Nm,

d=50x10^-3  mm

For soup bubble, P

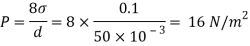
The pressure inside a soup babble is 16 N/m2

Q29) If the surface tension at air water interface is 0.075 N/m, what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?

A29)

Given:

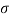  water = 0.075N/m,

d=0.01mm

An air bubble has only one surface,

The pressure difference between inside and outside of an air bubble is P=30000N/m2

Q30) What force is necessary to it a thin platinum wire ring of negligible thickness having 5 cm diameter from a water surface? Neglect weight of wire and consider surface tension of water as 0.0725 Nm.

A30)

Given: -

= 0.0725 N/m,

D= 5 cm = 0.05m

Force required to lift a than wire ring

Q31) A 10 mm glass tube is inserted into trough containing mercury. Find the capillary effect when the contact angle is: () 180 and (0) 110 Take surface tension of mercury in contact with air as 0.51 N/m. Dec. 2014.3 Marks

A31)

Given: d = 10 mm= 10 x 10 m,

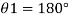
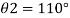
For mercury p=13600 kg/m²

To find: Capillary effect

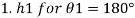
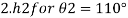
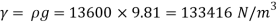
1)     Case 1: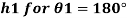

Weight density for mercury

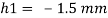
Negative sign indicates capillary depression.

2)     Case 2: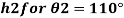

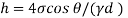
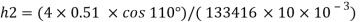
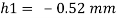
Negative sign indicates capillary depression

Q32) Two wide clean glass plates are held parallel with a gap of 1mm between them. What will be the rise of water level between these plates when dipped in water? Assume surface tension for water as 0.0730 N/m.

A32)

Given:

t=gap=1 mm

=0.073 N/m

For two wide clean glass plates,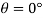

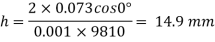
Capillary rise is 14.9 mm.

Q33) A clean tube of internal diameter 3 mm is immerged in a liquid with a coefficient of surface tension 0.48 N/m. Angle of contact of the liquid with the glass can be assumed to be 130%. The density of the liquid is 13600 kg/m". What would be the level of the liquid in the tube relative to the free surface of the liquid outside the tube?

A33)

Given:

d= 3 mm,

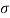= 0.48 N/m

The capillary rise (or depression) is given as

For mercury = 130°. 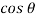=-0.6428

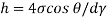
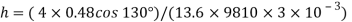
h= - 3. 083 mm

The negative sign indicates that there is capillary depression.

Q34) Find the height through which water rises by capillarity action in a glass tube of 2 mm bore, if the surface tension at the prevailing temperature is 0.0736 N/m. Assume angle of contact of glass with water -0°

A34)

Diameter of glass tube d=2 mm=2x10-3 m

Surface tension=0.0736 N/m

Angle of Contact

Capillary rise

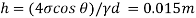
h= 15 mm

The height by which water rises by capillary is 15 mm.

Q35) A glass tube of internal diameter 0.2 mm is immersed in mercury. The angle of contact of mercury with glass can be taken as 130 W lat will be the level of Hg in the tube relative to the free surface of the liquid outside the tube? Take surface tension of liquid = 0.5 N/m Dec. 2010, 6 Marks

A35)

Given: d= 0.2mm,

0.5 N/m

The capillary rise (or depression) is given as

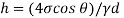
For mercury

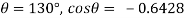
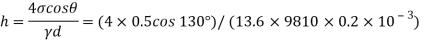
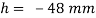
The negative sign indicates that there is capillary depression.

Q36) Determine the minimum size of glass tube that can be used to measure water level, if the capillary rise in the tube is not to exceed 0.25 mm, Take surface tension of water in contact with air as 0.0735 N/m. May 2013, 6 Marks

A36)

Given:

h=0.25 mm,

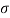=0.0735 N/m,

To find: Minimum size of glass tube 'd'.

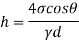
For water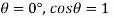

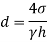
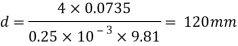
Q37) State the minimum diameter of glass tube to be immersed in water, for which capillarity effects are to be limited up to 2.08mm Take surface tension of water in contact with air as 0.073 N/m.  June 2011; 2 Marks

A37)

Given:

h=298mm,

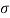=0.073 N/m,

for glass plates

To find: Diameter of tube,

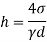
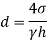
The diameter of glass tube immersed in water is 10 mm.

Q38) Determine the Bulk modulus of elasticity of a liquid, which is compressed in a cylinder from a volume of 0.0125 m³ at 80 N/cm² pressure to a volume of 0.0124 m³ at 150 N/cm² pressure?

A38)

Given:

Initial volume V = 0.0125 m²,

Final volume = 0.0124 m³

DV = Decreases in volume = 0.0125 -0.0124 = 0.0001m³

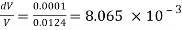
Initial pressure = 80 N/cm2

Final pressure - 150 N/cm

Increases in pressure = 150-80= 70 N/cm = 70 x 10^4 N/m²

Bulk modulus K

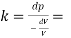Change in pressure/(change volume/ original volume)

The Bulk modulus of elasticity of a liquid is 56.79 x 10^6 N/m2

Q39) Determine the Bulk modulus of elasticity of a liquid, if the pressure of the liquid is increased from 400 Pa to 1200 Pa. The volume of the liquid decreases by 0.15% June 2010, 4 Marks

A39)

Given:

Initial pressure 400 Pa,

Final pressure 1200 Pa,

DV = 0.15% V

Increases in pressure

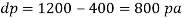
Decreases in volume

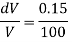
Bulk modulus

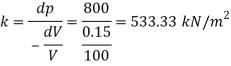
Q40) A cylinder contains a liquid of volume of 0.02 m' at pressure of 700 Pa when compressed to reach a volume of 0.019 m The pressure is increased to 1400 Pa. Find bulk modulus of elasticity Dec. 2011, 2 Marks

A40)

Given:

Initial volume 0.02 m²

Final volume 0.019 m

Change in volume dv=0.02- 0.019 = 1x 10^-3 m^3

Change in pressure dp = 1400-700 = 700 Pa

Bulk modulus k

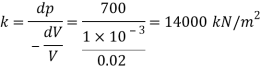
Q41) If the bulk modulus of elasticity of water is 2.07 x 10° kN/m²:

(1) What is the pressure required to reduce its volume by 2%?

(ii) What will be the change in mass density?

A41)

Given:

K=207 x 10 kN/m²

DV/V= 2%

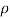for water = 1000 kg/m

To find: dp, d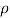

1)     Pressure required to reduced its volume by 2%

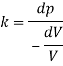
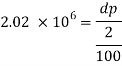
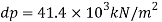
2)     Change in mass density

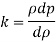
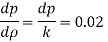
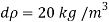
Q42) A pressure of 1.2 M Pascal is applied to 350 liters of liquid, causes a volume reduction of 1.5 liters. Calculate bulk modulus of elasticity for the liquid also find the compressibility.

A42)

Given:

Pressure p= 1.2M,

Pascal = 12x10 N/m².

Volume V 650 liter=  650 x 10³ m.

Reduction in volume dV= 1.5 liter=  1.5 x 10^-3 m3

Bulk modulus of elasticity, K

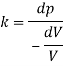
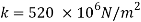
Compressibility

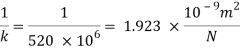
The Bulk modulus of elasticity for the liquid is 520 M Pa and compressibility is 1.923 x 10 m/N.

Q43) At a depth of 5 kilo meters in the ocean the pressure 480 kg/cm Assuming specific weight at the surface as is 1025 kgm and that the average modulus of elasticity is 24 x 10 kg/cm for that pressure range. Calculate:

a) The change in specific volume between the surface and the given depth

b) Specific volume at the given depth and

c) Specific weight at that depth.

A43)

Given:

Pressure dp = 480 kg/cm²

Average modulus of elasticity K = 24 x 10' kg/cm

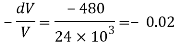
Specific volume of the water at the surface of the ocean,

Specific volume

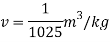
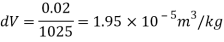
Specific volume at the depth of 5 km,

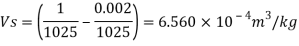
Specific weight of water at the depth of 5 km,

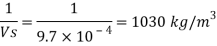
Q44) At a depth of 2 km in an ocean, the pressure is 840 bar. Assume the specific weight at surface as 10,250 N per m² and the average Bulk modulus of elasticity as 2.4 x 10° kN per sq.m. For that pressure range.

1) What will be the change in specific volumes between that at the surface and at that depth?

2) What will be the specific volume at that depth?

3) What will be the specific weight at that depth?

A44)

Given:

P₁ = 840 x 10¹ Pa,

H1, = 2 km = 2000 m.

 = 10250 N/m²,

K = 2.4 x 10' Pa

Bulk modulus K

And

Specific volume

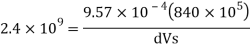
Change in specific volume

Specific volume at 2 km depth

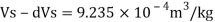
Density at 2 km depth

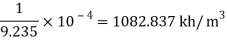
Specific weight

Unit - 1

Basic Concepts and Definition

Q1) Explain distinction between fluid and solid?

A1)

• We have a common, vague idea of ​​difference. Solid is not easily damaged; and the liquid is easily deformed (we can easily move through the air).
• Although it is quite descriptive, this unusual view of the difference between solids and liquids is not very satisfying from a scientific or engineering point of view.
• The obvious difference is based on bow items that are disabled under the action of the external load.
• Fluid is defined as a substance that progressively deforms when subjected to shear stress of any size.
• The shear pressure (force at the per unit area) is created whenever the tangential force is applied to the surface as shown to the individual.
• When solid foods such as iron or other metals are subjected to shear pressure, they will initially be disabled (usually the smallest factor), but they will not continue to degenerate (flow).
• However, common liquids such as water, oil, and air satisfy the definition of liquid — that is, they will flow when they are made by shear pressure.
• Some materials, such as slurries‚ tar, putty, toothpaste, etc., are not easily separated because they will behave stronger if the shear pressure applied is less, but if the pressure exceeds a certain critical amount, the object will move.
• The study of such materials is called Rheology and does not fall into the category of classical fluid mechanics.
• Although the formation of fluid cells is important in the separation of fluids from one another, due to the large number of molecules involved, it is impossible to study the behavior of individual molecules when attempting to explain the function of a liquid at rest or on the move.
• Instead, we demonstrate this behavior by considering the scale, or macroscopic. The amount of interest rate, when the ratio is tested over a small volume containing a large number of molecules.

Q2) Explain density, Specific weight?

A2)

• Quantity (precisely, the size of the volume of a volume; also known as a specific weight), of an object whose weight is the volume of the unit.
• The symbol most commonly used for congestion is ρ (the capital letter of the Greek word rho), although the Latin letter D may also be used. Statistically, quantity is defined as the quantity divided by volume

ρ = m/ v

• Where ρ size, m size, and V is volume. In some cases (for example, in the United States oil and gas industry), overcrowding is freely defined as its weight per unit volume, although this is scientifically incorrect - this number is specifically called a specific weight.

• Pure material overcrowding has the same value as its mass concentration.
• Different materials tend to have different strengths, and congestion can be accompanied by durability, purity and packaging.
• Osmium and iridium are the most well-known substances in normal temperature and pressure conditions.

• To facilitate quantitative comparisons in various unit systems, sometimes incorporating an empty value "related size" or "specific gravity", e.g. A measure of the quantity of an object in that of a normal object, usually water. So the relative density of less than one relative in water means that the object is floating in water.

• The quantity of matter varies with temperature and pressure. These variations are usually small in solids and liquids but very large in gases. Increasing the pressure on an object reduces the volume of the object and thus increases its size.
• Increasing the temperature of an object (with a few exceptions) reduces its size by increasing its volume. In many cases, heating the bottom of the liquid leads to a temperature rise from the bottom to the top, resulting in a decrease in the volume of this warm liquid. This causes it to rise in relation to dense non-heated objects.

• The multiplication of quantities of matter is sometimes called its specific volume, which is a term sometimes used in thermodynamics. Quantity is a powerful structure in that the increase in the number of objects does not increase its size; instead it increases its weight.

Measurement of density

• There are many strategies and levels to measure the size of the materials used. Such techniques include the use of a hydrometer (fluid rehydration method), Hydrostatic balance (fluid and firmness method), an immersive body system (beverage fluid method), pycno meter (fluid and solids), air comparisons pycno meter (solid), oscillating densitometer (liquid), and pour and tap (solid).
• However, each method or procedure measures different types of quantities (e.g. Density, bone size, etc.), so it is necessary to understand the type of density measured and the type of object in question.

Homogeneous material

• The plurality of all the points of an object corresponding to its equality and its magnitude is divided by its total volume. Weight is usually measured in scale or balance; volume can be measured directly (from the geometry of an object) or by liquid transfer. To determine the size of the liquid or gas, hydrometer, dasy meter or Cororiol is flow meter can be used, respectively. Similarly, a hydrostatic weight uses water migration due to the immersed material to determine the size of the object.

Heterogeneous material

• When the body is incompatible, its homosexuality varies between different regions of the object. In that case the congestion around any given area is determined by the calculation of the maximum volume around that area. At the lowest volume limit the density of the non-point object

m = integration v ρ (r)d V

Non compacted material

• In practice, bulk materials such as sugar, sand, or ice contain voids. Many substances exist in nature such as flakes, pellets, or granules.

• Voids are regions that contain something other than imaginary objects. Normally this void is air, but can also contain vacuum, liquid, solid, or a different gas or gas mixture.

• Bulk volume - including an empty fraction - is usually obtained by simple measurement (e g by measuring cup measurement) or by geometry from known sizes.

• Mass divided by the volume of the pile determines the congestion of the pile. This is not the same as volumetric mass.

• To determine the size of the weight of the volume, one must first reduce the volume of the missing portion. Sometimes this can be determined by geometric thinking. Close packaging for equal parts of the empty fraction can be at least 74%.
• It can also be determined by force. Some materials in bulk, however, like sand, have a flexible fraction that depends on how the material is moved or poured. It may be loose or compact, with more or less air space depending on the handling.

• In practice, an empty fraction is not just air, or gas. In the case of sand, it could be water, which would be useful to measure as the empty fraction of sand filled with water - once all the air bubbles have been removed - can be much more flexible than dry sand compared to empty air.

• In the case of non-composite materials, one should also be careful in determining the size of the material sample.
• If the material is under pressure (the frequency of bad air on the surface of the earth) the determination of the weight from the measured sample scale may need to respond to the effects of the stiffness due to the quantity of the empty material, depending on how the measurement is made.
• In the case of dry sand, sand is so thicker than air that the softening effect is often overlooked (less than one thousandth).

• Mass conversion when removing one empty object and another while maintaining a constant volume can be used to measure the empty fraction, if the difference in the size of the two empty objects is reliably known.

SPECIFIC WEIGHT

• A specific weight, also known as a unit weight, is the unit weight of an item.
• The most commonly used value of the Earth's water table is 4 ° C, which is 9.807 k N / m3 or 62.43
• Gravity words, and very unusual weights, are used for relative size. A common symbol of a certain weight is γ, the Greek letter Gamma.

Definition

• The specific weight, γ, of a story is defined as the product of its plurality, ρ, and the common gravitational force, g: Gamma = ρ g
• Quantity of matter is defined as quantity by unit volume, typically measured in kg / m3. Gravity is usually faster due to gravity, usually given in m / s2, and on Earth it is generally considered to be 9.81 m / s2.
• Unlike quantity, a certain weight is not a fixed asset. Depending on the speed of gravity, it varies from place to place. Pressure can also affect values, depending on the bulk modulus of the object, but often, at moderate pressure, it has a less significant effect than other factors.

Q3) Explain specific gravity?

A3)

• The relative quantity or gravitational force is a measure of the size (volume of a unit volume) of an object in the quantity of a given object.
• The gravitational force of the liquid is almost always measured in relation to the water obtained (at 4 ° C or 39.2 ° F); for gases, the reference is air at room temperature (20 ° C or 68 ° F). The term "relative congestion" is often popular in scientific practice.

• If the density of an object is less than 1 it means that it is more dense than the reference; if it is greater than 1 then it is thicker than the reference.
• If the relative size is 1 exactly the stiffness is equal; that is, equal amounts of these two objects have the same weight. If the reference is water, then an object with a relative mass (or certain gravitational force) less than 1 will float in the water.
• For example, an ice cube, with a relative weight of about 0.91, floats. An object with a relative weight greater than 1 will sink.

• Temperature and pressure should be specified on both the sample and the reference. The pressure is approximately 1 atm (101.325 kPa). When not, it is very common to specify the exact size. Sample and reference temperatures vary from industry to industry.
• In British brewing practice, gravity, as described above, increased by 1000. Certain gravity is widely used in the industry as an easy way to obtain information about the complexity of solutions for various substances such as brines, sugar solutions (syrups, juices, honeys, brewers wort, must, etc.) and acids.

Uses

• The quantity associated with it can help to measure the maturity of a liquid or a gas, or determine the density of an unknown substance from a known congestion in another. Related quantities are often used by geologists and mineralogists to help determine the mineral content of a rock or other sample.
• Gemologists use it as an aid in the identification of gemstones. Water is preferred as a reference because measurements are easy to make in the field (see below for examples of measuring methods).

• As the basic application of industrial quantity measurements in the industry the determination of the focus of objects is a powerful solution and this finding in the RD vs concentration tables is very important for the analyst to enter the table in the correct way for the related quantities.
• For example, in the brewing industry, the Plato table, which calculates the concentration of sucrose in large quantities against real RD, initially (20 ° C / 4 ° C) based on the weight estimates of sucrose solutions made at laboratory temperatures (20 ° C) but with reference to positioning of water at 4 ° C very close to temperatures where the water has its maximum H (H) magnitude 2O) equal to 0.999972 g / cm3 (or 62.43 lb · ft - 3).
• The ASBC table used today in North America, when based on Plato's original table is the apparent average size of (20 ° C / 20 ° C) on the IPTS-68 scale where the water level is 0.9982071 g / cm3. In sugar, soft drinks, honey, fruit juice and sucrose-related industries the mass extraction is taken from this SG-using activity (17.5 ° C / 17.5 ° C). As a final example, British RD units are based on a reference temperature with a sample of 60 ° F and thus (15.56 ° C / 15.56 ° C).

Q4) Explain kinematic and dynamic viscosity?

A4)

Dynamic Viscosity

Absolute viscosity - the coefficient of total viscosity - is the measure of internal resistance. Dynamic (absolute) viscosity is the tangential force at each unit area required to move one horizontal plane in relation to another plane - by unit velocity - while maintaining unit distance outside the fluid.

Shave pressure between layers of fluid in straight lines can be defined by Newtonian fluid as

Liquid - viscosity and velocity profile

Fig no 1 Dynamic and kinematic viscosity

Shear depression can be shown

τ = μ dc / d y

   = μγ.                                  ........   (1)

Where

τ = cutting pressure on liquid (N / m2)

μ = strong viscosity of liquid (N s / m2)

d c = unit velocity (m / s)

d y = unit distance between layers (m)

γ = dc / d y = shear rate (s-1)

Equation (1) is known as the Newtons Law of Friction.

(1) Can be rearranged to reflect Dynamic viscosity as

μ = τ dy / dc

      = τ / γ.                                     .......... . (1b)

• In the SI system the dynamic viscosity units are N s / m2, Pa s or kg / (m s) - where

1 Pa s = 1 N s / m2 = 1 kg / (m s) = 0.67197 lbm / (ft s) = 0.67197 slug / (ft s) = 0.02089 lbf s / ft2

• Strong viscosity can also be expressed in the metric CGS system (centimeter-gram-second) such as g / (cm s), dyne s / cm2 or poise (p) where

1 poise = 1 dyne s / cm2 = 1 g / (cm s) = 1/10 Pa s = 1/10 N s / m2

• Effective use Poise is usually very large and the unit is therefore divided by 100 - into a small centipoise (cP) unit - where

1 P = 100 cP

1 cP = 0.01 poise = 0.01 gram per cm second = 0.001 second Pascal = 1 milliPascal second = 0.001 N s / m2

20.2oC (68.4oF) liquids have a perfect viscosity of one - 1 –centiPoise.

Kinematic Viscosity

Kinematic viscosity is a measure of the total viscosity - (or intensity) of a quantity - the amount of non-energy. Kinematic viscosity can be obtained by dividing the total viscosity of the liquid by the amount of fluid mass

ν = μ / ρ                               .................. (2)

Where

ν = kinematic viscosity (m2 / s)

μ = full or strong viscosity (N s / m2)

ρ   = density (kg / m3)

In the SI-system the unit of kinematic viscosity theory is m2 / s - or the most commonly used Stoke (St) where

• 1 St (Stokes) = 10-4 m2 / s = 1 cm2 / s

Stoke comes from the CGS unit program (Centimeter Gram Second Second).

As the Stoke unit is usually divided by 100 into smaller units centi Stoke (c St) - there

• 1 St = 100 c St

• 1 c St (centi Stoke) = 10-6 m2 / s = 1 mm2 / s

• 1 m2 / s = 106 centi Stokes

The gravitational force of 20.2oC (68.4oF) is almost the same, and the kinematic viscosity of 20.2oC (68.4oF) water is designed to operate 1.0 mm2 / s (c Stokes). The most precise water viscosity at 20.2oC (68.4oF) is 1.0038 mm2 / s (c St).

Conversion from full viscosity to kinematic in Imperial units can be shown as

ν = 6.7197 10-4 μ / γ.                           .................... (2a)

Where

ν = kinematic viscosity (ft2 / s)

μ = full or strong viscosity (c P)

γ = specific weight (lb / ft3)

Q5) Explain variation of viscosity with temperature?

A5)

• The viscosity of the fluid is due to two contributing factors, namely the interaction between fluid molecules and the transfer of pressure between molecules. In the case of gases the penetration between molecules is large and therefore the interaction of molecules is small.
• But in terms of liquid the molecules are very close together and as a result there is a great deal of interaction. Thus in liquids, viscosity is mainly due to the interaction of the middle cells, while in gases the viscosity is mainly due to the transfer of molecular pressure.
• The bonding force of the molecule decreases with increasing temperature and therefore with increasing temperature the viscosity of the liquid decreases.

The following formula provided by Poiseuille shows the dependence of the viscosity of the liquid on the heat-

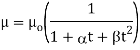
Where, 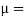Viscosity of the liquid at C in poise

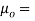Viscosity of the liquid at 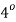C in poise

 and are constant characteristics of the liquid.

For water,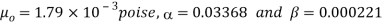

• In the case of gases, as mentioned earlier, the combination of molecules can be ignored viscosity depends largely on the transfer of molecular pressure on the right side to the direction of motion. As the temperature increases the movement of the cells increases that is, there will be a greater transfer of pressure and therefore the viscosity increases. Holman gave the following statement on gas viscosity-
• 

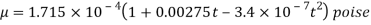
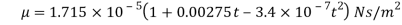
Viscosity of Liquids

Liquid	Viscosity at various temperatures
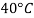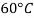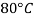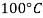Water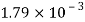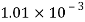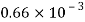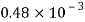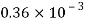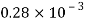
Alcohol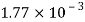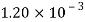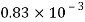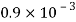
Kerosene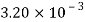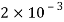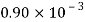
Petrol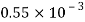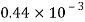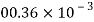

Viscosity of Air at various Temperature

Temperature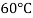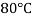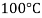
Viscosity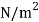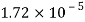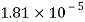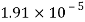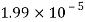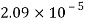

Q6) Explain Newton’s law of viscosity and vapor pressure?

A6)

Newton's viscosity law states that the shear pressure between adjacent water layers is equal to the velocity gradients between these two layers.

The shear pressure ratio and shear ratio are constant, at a given temperature and pressure, and are defined as viscosity or coefficient of viscosity.

Newton’s Law of viscosity,

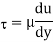
Where,

Viscosity

Shear stress=F/A

Rate of shear deformation

Vapour Pressure

• Vapor pressure (or vapor pressure in British English; see spelling difference) or equilibrium moisture pressure is defined as the pressure exerted by the smoke on the thermodynamic equilibrium and its thick (solid or liquid) phases at a given temperature in a closed system.
• Equilibrium pressure is an indicator of evaporation rate. It is related to the tendency of particles to leak into a liquid (or solid). An object with a high vapor pressure at normal temperatures is often called an invariant.
• The pressure exerted by evaporation over a liquid is known as vapor pressure. As the temperature of a liquid increases, the kinetic energy of its molecules also increases.
• As the kinetic energy of the molecules increases, the number of molecules that evaporates also increases, thus increasing the vapor pressure.

Fig no 2 Vapour pressure

• The vapor pressure of any substance increases with the temperature according to Clausius- Clapeyron's relationship. The atmospheric pressure of boiling liquid (also known as the normal boiling point) is the temperature at which the pressure of the vapor is equal to the atmospheric pressure of the atmosphere.
• With the increasing temperature of that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and to raise the liquid to form vapor bubbles inside the object.
• The formation of a deep bubble in a liquid requires a high temperature due to the high pressure of the liquid, because the pressure of the liquid rises above the atmospheric pressure as the depth increases.
• The most important thing at the deepest depth is the high temperature needed to start bubble formation. The friction of the surface of the bubble wall leads to excessive pressure on very small, initial bubbles.
• The vapor pressure that one part contributes to total pressure in the system is called incomplete pressure. For example, sea air, and filled with water vapor at 20 ° C, has incomplete water pressures of about 2.3 k Pa, 78 k Pa of nitrogen, 21 k Pa of oxygen and 0.9 k Pa of argon, a total of -102.2 k Pa, which forms the basis of the normal atmospheric pressure.

Measurement and uses

• Vapor pressure is measured in standard pressure units. The International System of Units (SI) recognizes pressure as a unit derived from the magnitude of energy in each area and defines pascal (Pa) as its standard unit. One pascal is a newton per square meter (N · m - 2 or kg · m - 1 · s - 2).
• The pulse pressure test measurement is a simple procedure for normal pressures of between 1 and 200 k Pa. The most accurate results are found near the boiling point of objects and large errors result in smaller doses than 1kPa.
• Procedures usually include cleaning the test object, separating it from the container, removing any foreign gas, and then measuring the equilibrium pressure of the gas phase of the object in the container at various temperatures.
• Better accuracy is achieved when care is taken to ensure that everything and its vapor are at a set temperature. This is usually done, such as using an isotonic scope, by inserting the contents of the liquid in a liquid bathtub.
• Very low vapor pressure of solids can be measured using the Knudsen cell method
• According to medical conditions, vapor pressure is sometimes expressed in other units, especially millimeters of mercury (mmHg). This is important for flexible anesthetics, most of which are body fluids, but with very high vapor pressure.

Q7) Explain boiling point and cavitation?

A7)

Boiling Point

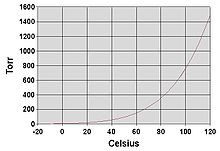
Fig no 3 Boiling point

• The boiling point of a liquid varies depending upon the surrounding environmental pressure. A liquid in a partial vacuum has a lower boiling point than when that liquid is at atmospheric pressure.
• A liquid at high pressure has a higher boiling point than when that liquid is at atmospheric pressure. For example, water boils at 100 °C (212 °F) at sea level, but at 93.4 °C (200.1 °F) at 1,905 meter (6,250 ft) altitude. For a given pressure, different liquids will boil at different temperatures.
• The normal boiling point (also called the atmospheric boiling point or the atmospheric pressure boiling point) of a liquid is the special case in which the vapor pressure of the liquid equals the defined atmospheric pressure at sea level, one atmosphere.
• At that temperature, the vapor pressure of the liquid becomes sufficient to overcome atmospheric pressure and allow bubbles of vapor to form inside the bulk of the liquid. The standard boiling point has been defined by IUPAC since 1982 as the temperature at which boiling occurs under a pressure of one bar.

• The heat of vaporization is the energy required to transform a given quantity (a mol, kg, pound, etc.) of a substance from a liquid into a gas at a given pressure (often atmospheric pressure).

• Liquids may change to a vapor at temperatures below their boiling points through the process of evaporation. Evaporation is a surface phenomenon in which molecules located near the liquid's edge, not contained by enough liquid pressure on that side, escape into the surroundings as vapor.
• On the other hand, boiling is a process in which molecules anywhere in the liquid escape, resulting in the formation of vapor bubbles within the liquid.

• Like all liquids, water evaporates when its vapor pressure reaches its surrounding pressure. Naturally, atmospheric pressure is low at high altitudes and water boils burn low. The boiling water temperature of atmospheric pressure can be compared to the Antoine equation:

Log 10 (P/ 1 Torr) = 8.07131 -[( 1730.63 °c) / (233.426° c + Tb)]

• Or transportation into this temperature explicit form

Tb = [1730.63 °c/ (8.07131 - log 10(P/ 1 Torr))] - 233

Where the temperature Tb is the boiling point in degree Celsius and the pressure P is in Torr

Relation between the normal boiling point and the vapour pressure of liquid

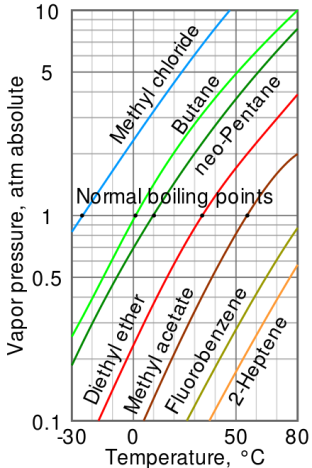
Fig no 4 Log linear Vapour pressure chart

• The steam pressure chart on the right contains graphs of vapor pressure relative to the temperature of the various beverages. As can be seen from the chart, beverages with very high vapor pressure have very low boiling points.
• For example, at any given temperature, methyl chloride has the highest pressure of any gut in the liquid on the chart. It also has the lowest boiling point (-24.2 ° C), at which point the methyl chloride pressure curve (blue line) crosses the horizontal pressure line of one atmosphere of absolute vapor pressure.
• The critical point of the liquid is the very high temperature (and pressure) that it will boil.

Cavitation

• Cavitation is a process in which a decrease in pressure to or under pressure from a liquid vapor leads to the formation of vapor-filled pores in the liquid. When placed under high pressure, these gaps, called "bubbles" or "voids", collapse and can create shocking waves that can damage equipment. These shock waves are strong when they are very close to the inserted bubble, but they quickly become weak as they spread away from the insert

• Cavitation is an important cause of wear in some engineering situations. The collapse of the voids entering near the metal causes cyclic stress through repeated implosion. This causes excess fatigue of the metal which causes a type of wear also called "cavitation". The most common examples of this type of wearable pumping equipment, and bending where there is a sudden change in the flow of fluid. Cavitation is usually divided into two behavioral categories: inertial (or temporal) cavitation and non-inertial cavitation.

• The process by which a void or bubble in a liquid falls rapidly, producing a shock wave, is called an inertial cavitation. Inertial cavitation occurs naturally in strikes of shrimp and pistol shrimps, as well as plant tissue. In man-made objects, it is possible for control valves, pumps, propellers and power inserts.

• Non-inertial cavitation is a process in which a bubble in a fluid is forced to change in size or shape due to some form of energy input, such as an acoustic field. Such cavitation is commonly used in ultrasonic cleaning facilities and can also be seen in pumps, propellers, etc.

• Since shock waves formed by collapsing spaces are strong enough to cause significant damage to parts, cavitation is often undesirable to machinery (although desirable when used intentionally, for example, sterilizing contaminated surgical instruments, dissecting contaminants in water purification systems, emulsify tissue cataract surgery or lithotripsy of kidney stones, or homogenize fluids). Special protection is often avoided in the construction of turbines or propellers, and eliminating cavitation is a major field in the study of fluid dynamics. However, sometimes it helps and does not cause damage when the bubbles fall away from the equipment, such as at high altitudes.

• Cavitation can occur when the local pressure in a liquid reaches a level below the pressure of the liquid vapor at the actual temperature. According to the Bernoulli Equation this can happen if the fluid accelerates to a control valve or to a pump-in area.

• Vaporization itself does not cause damage - damage occurs when the vapor almost immediately after evaporation decreases when the velocity decreases and the pressure increases.

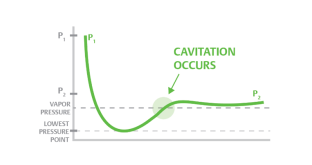
Fig no 5 Cavitation

Avoiding Cavitation

Cavitation can be generally avoided

• Increase the distance (pressure difference) between the actual static pressure on the liquid - and the pressure of the liquid vapor at direct temperature

This can be done by:

• Regenerative engineering components that initiate high speeds and low static pressures
• To increase the total or local pressure in the system
• To reduce the temperature of the liquid

Redesign Components Launch High Speed ​​and Low Static Pressure

Walking and injury can be avoided by using special equipment designed for extreme conditions.

• Situations with large pressure drops can be handled by Multi Stage Control Valves
• Challenging pump conditions with fluid temperatures near vaporization temperature can be treated with special pumps - performance behind other conditions than centrifugal pumps

Increasing total or local pressure in the system

• By increasing the total or local pressure in the system the distance between stationary pressure and vaporization pressure increases and vaporization and cavitation can be avoided.
• The balance between stationary pressure and vaporization pressure - an indication of possible vaporization, is often expressed by Cavitation Number.
• Unfortunately it is not always possible to increase the total static pressure due to system configuration or other limitations. Local static pressure in some parts can increase by lowering (rising) part of the system. Control pipes and pumps should usually be placed at the lowest point of the system to raise the immovable head.
• This is a common solution for boiler feed pumps that receive hot condensate (water up to 100 °C) from condensate receivers in steam plants.

Q8) Explain surface tension?

A8)

• Surface tension is the tendency for the liquid to shrink into the smallest possible area. Facial friction allows insects (e.g. Water arrows), to float and slide on the surface of water without immersion.
• Where fluids combine with air, the resulting incompatibility arises from the greater attraction of liquid molecules to each other (due to bonding) than to air molecules (due to adhesion).
• There are two main processes in play. One is the internal energy of the extra molecules that make the liquid enter. The second is the gravitational force associated with the surface of the membrane. The effect of the net is that the liquid behaves as if its surface was covered with a thick membrane.
• Due to the high attraction of water molecules to each other through the hydrogen bond web, water with a surface elevation (72.8 millinewtons (mN) per meter at 20 ° C) than most other beverages. Facial incompatibility is an important factor in the case of capillarity.
• Extra tension is a measure of the strength in the length of each unit, or the strength in the area of ​​each unit. This is similar, but when referring to the energy in each unit area, it is common to use the term energy energy, which is a common term in the sense that it also applies to solids.
• In science fiction, ground tension is applied either to the pressure of the earth or to higher forces.

Causes

• Due to the relative strength the molecule is pulled evenly on all sides by neighboring chemical molecules, resulting in zero energy. The upper molecules do not have the same molecules on all sides so they are pulled inwards. This creates some internal pressure and forces wet areas to penetrate that small area.
• There is also a surface tension in the liquid-air optical connector that will withstand external forces, due to the interaction of water molecules.
• The gravitational force that works between molecules of the same type is called cohesive force and those that work between molecules of different types are called cohesive forces.
• The balance between fluid mixing and its adhesion to the contents of the container determines the water level, contact angle and position of the meniscus. When cohesion dominates (preferably, the adhesion capacity is less than half the cohesive force) the moisture is low and the meniscus pulls against a straight wall (with respect to mercury in a glass container).
• On the other hand, when adhesion controls (the holding capacity of more than half of the cohesive force) the moisture is high and the same meniscus is concave (as in water in a glass).
• Facial tension is the result of the formation of water droplets. Although easily deformed, water droplets tend to be drawn in an unequal circular motion on the overlapping forces of the upper layer. In the absence of additional energy, droplets of almost all liquid may be round. The rounded shape reduces the "wall friction" required by the upper layer according to Laplace law.
• Another way to look at surface tension is power. A molecule that communicates with a neighbor is in a lower state of energy than it is alone.
• Internal molecules have as many neighbors as possible, but boundary molecules are lost in the neighborhood (compared to internal molecules) and therefore have higher potency.
• In order for a liquid to reduce its energy level, the number of molecules at higher energy limits must be reduced. A reduced number of boundary molecules leads to a much lower surface area.
• As a result of the reduction in area, the area will take on the potential smoothness (statistical evidence that the "smooth" formation reduces the surface area depending on the use of the Euler-Lagrange figure). Since any curvature of the impact shape results in a larger area, there will be higher strength.

Effect of surface tension

Water

Many of the effects of global conflict can be seen in ordinary water:

• Beads of rain water on the surface of the wax, like a leaf. Water adheres weakly to melt and solidify itself, so water collections become droplets. Extra tension gives them their intimate circular shape, because the field has the smallest area over the volume size.

Fig no 6 Water bending on leaf

• The formation of droplets occurs when the weight of the liquid is increased. Flushing (below) indicates that water is attached to the mains for maximum gain until it is extended to an area where ground height can no longer keep the pump connected to the tap. After that it separates and the surface tension creates a partial reduction. When a stream of water flowed out of a tap, the river broke in pieces when it fell. Gravity lightens the stream, and the moisture of the earth drains you into the fields.

Fig no 7 Water dripping from a tap

• The movement of thick objects in water occurs when an object is not soft and its weight is small enough to be carried by forces from the earth's crust. For example, water abusers use ground tension to move on the surface of a lake in the following way. The dehydration of the water rider's leg means that there is no attraction between the leg molecules and the water molecules, so when the leg moves down into the water, the surface tension of the water tries to restore its softness to its flexibility due to the leg. This water behavior pushes the water rider up so that you can stand on the water as long as its weight is small enough for the water to support it. The surface of the water acts like an expanding film: the feet of the insect cause cracks in the surface of the water, increase the surface area and the tendency to decrease the earth's curv (such surface) water pushes the insect's feet upwards.

Fig no 8 Water striders stay atop the liquid because of surface tension

• The separation of oil and water (in this case, water and liquid wax) is caused by a facial imbalance between different drinks. This type of ground tension is called "interface tension", but its chemistry is the same.

Fig no 9 Lava lamp

• Tears of wine the formation of drops and streams along a glass containing an alcoholic beverage. The reason for this is the complex interaction between the different surface tension of water and ethanol; a combination of water-soluble changes by ethanol and ethanol evaporates faster than water.

Fig no 10 Tears of wine

Surfactants

Surface tension is seen in other common causes, especially when surfactants are used to reduce it:

• Soap bubbles have very large areas with very small size. The foam in the clear water is unstable. The addition of surfactants, however, can have a stabilizing effect on bubbles (see Marangoni effect). Note that surfactants actually reduce water resistance by a factor of three or more.
• Emulsions are a type of colloid in which the surface of the earth plays a role. Smaller pieces of oil suspended in pure water will automatically merge into larger masses. But the presence of the surfactant provides a decrease in surface tension, which allows for the stabilization of the minute droplets of oil in most liquids (or vice versa).

Q9) Explain capillarity?

A9)

• Capillary action (sometimes capillarity, capillary motion, capillary effect, or wicking) is the ability of fluid to flow in small areas without assistance, or even to counteract external forces such as gravity.
• The effect can be seen in the formation of fluid between the hairs of the paint brush, in a thin tube, in the smooth material such as paper and cement, in other non-abrasive materials such as sand and carbon fiber, or organic cell.
• It occurs due to intermolecular forces between liquids and solid surrounding environments. If the diameter of the tube is small enough, then a combination of ground incompatibility (caused by coagulation within the liquid) and the ability to adhere between the wall of the liquid and the vessel to form a liquid.
• The first recorded view of the capillary act was by Leonardo da Vinci. A former Galileo student, NiccoloAggiunti, was said to be investigating the carrying of the wheels.
• By 1660, capillary action was still a novelty for Irish chemist Robert Boyle, when he reported that "some Frenchmen wanted to know" realized that when the capillary tube was submerged in water, the water would rise "up into the Pipeline". Boyle then reported on a trial in which he put a capillary tube in red wine and then inserted a tube.
• You have found that the vacuum has no visible effect on the rise of the fluid in the capillary, so the performance of the fluid in the capillary tubes is due to a specific condition different from that which controls the barometers baro meters.
• Some quickly followed Boyle's lead. Some (e.g., HonoreFabri, Jacob Bernoulli) thought that fluid was rising in the capillaries because air could not enter the capillaries as easily as fluid, so air pressure was lower within the capillaries.
• Some (e.g., Isaac Vossius, Giovanni Alfonso Borelli, Louis Carre, Francis Hauksbee, Josia Weitbrecht) thought that liquid particles were attracted to each other and capillary walls.
• Although experimental studies continued through the 18th century, effective treatment of capillary values ​​up to 1805 by two researchers: Thomas Young of the United Kingdom [16] and Pierre-Simon Laplace of France.
• They found the equivalent of the Young - Laplace capillary act. By 1830, German mathematician Carl Friedrich Gauss had determined the parameters of the capillary (i.e., conditions on a solid visual connection). Known as Kelvin's equation.
• German philosopher Franz Ernst Neumann (1798-1895) subsequently decided to collaborate between two non-alcoholic beverages.
• Albert Einstein's first paper, sent to Annalen der Physik in 1900, was astonishing.
• Capillary penetration into media sources shares its powerful equipment through the flow of empty tubes, as both processes are opposed by viscous force.
• As a result, the most common tools used to demonstrate this practice are capillary tube. When the lower end of the glass tube is immersed in fluid, such as water, the concave meniscus forms.
• Adhesion occurs between the fluid and the solid inner wall that pulls the liquid column until there is a sufficient amount of gravity force to overcome these intermolecular forces.
• The length of the contact (edge) between the top of the liquid column and the tube is equal to the width of the intestine, and the weight of the liquid column is equal to the square area of ​​the tube.
• Therefore, a narrow tube will pull the liquid column farther away from the broad bone, provided that the internal water molecules interact sufficiently with the outer ones.

Q10) Explain bulk modulus of elasticity and compressibility?

A10) An elastic modulus (also known as a modulus of elasticity) is a value that measures an object or object to the object of a highly deformed object (i.e., non-permanent) in which pressure is applied. The expandable modulus of the material is defined as the slope of the pressure point in the region of the elastic deformation: Solid material will have a very high modulus. The elastic modulus has the following form:

Delta = stress / strain

Where the pressure is the force that causes the change to be divided by the area in which the force and gravity are used is the rate of change of a particular parameter caused by the distortion in the actual parameter value. Since the difficulty is flawless, the delta will be the same as the units of pressure.

Determining how pressure and complexity will be measured, including indicators, allows for many types of expandable model to be defined. The three main ones are:

1. The Young (E) modulus defines a solid, or tilt, inclination of an object along the axis when opposing forces are used on that axis; defined as a measure of the severity of the stiffness of the stiffness. It is often referred to as the elastic modulus.
2. The shear modulus or stiffness modulus the second parameter of Lame) defines the tendency of an object to shave (change in shape with a fixed volume) when operated by opposing forces; is defined as the shear pressure above the shear type. The shear modulus is part of the viscosity detection.
3. The modulus in the plural (K) defines volumetric stiffness, or the tendency of an object to deform in all indicators when loaded equally in all indicators; is defined as the volumetric pressure over the volumetric mass, and the opposite of the pressure. Modulus in bulk extension of Young's modulus has been in three dimensions.

• Two other extensible methods are Lames first parameter, λ, and P-wave modulus, M, as used in the modulus comparison table given below.

• Homogeneous and isotropic substances (the same in all directions) (solids) have their own (linear) stretchy properties that are fully defined by two stretchable conditions, and one can choose any pair. Given the expansive module, all other expandable methods can be calculated according to the formulas in the table at the bottom of the page.
• Liquids are special because they cannot support shear stress, which means the shear modulus remains zero. This also means that Young's modulus of this group remains a point.

• In some texts, the modulus of elasticity is called constant elastic, and most sizes are called modulus elastic.

COMPRESSIBILITY

• Compression is an asset to be reduced to a minimum by pressure. This material is the result of porosity, and the change in mass occurs from particles that come close together by pressure.
• Liquid pressure is actually a measure of the change in the quantity that will be produced in a liquid by a certain change. Gases, in general, are highly compressed and most liquids have very low pressures.
• The fact that the effects of stress can have a profound effect on the flow of fluid. The study of this flow when changes in quantity and temperature are most important is what is known as compressible flow fluid or gas dynamics.

Q11) Density of liquid is 850 kg/m³. Determine relative density and weight density of the liquid. With reason state whether the liquid will float on water or not

A11)

Gives:

p= 850kg/m'.

P. 1000kg/m (standard value)

To find: Relative density, weight density

Relative density

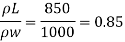
Weight density

The liquid will float on water because weight density of liquid is less than water.

Q12) On a certain planet a correctly calibrated spring balance shows the weight of a body s 12 N, the mass of which is 4.893 kg. Find the value of gravity on this planet.

A12)

Given:

Weight W= 12 N.

Mass m = 4.893 kg

Weight = Mass x acceleration

Acceleration due to gravity on a certain planet is 2.45 m/sec.

Q13) What is the specific volume of material with specific gravity 0.87?

A13)

Given:

Specific gravity=0.5,

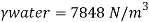
To find: Specific volume.

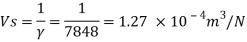
Q14) The specific volume of a certain gas is 0.7m/kg Determine its specific weight and mass density.

A14)

Given:

Specific volume =0.7

To find: Mass density, specific weight

Mass density (p)

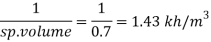
Specific weight (Y)

Q15) Calculate the specific weight, density, specific volume and relative duty of oil which 7 N per liter.

A15)

Given:

Weight W=7N,

Volume V= 1 litre = 10^-3 'm^3

To find:

Specific weight,

Specific volume,

Relative density

Specific weight Y

Density

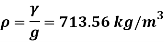
Specific volume (Vs)

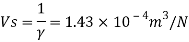
Relative density

Q16) 2 liter of petrol weighs 14N. Calculate the specific weight, density, specific volume and specific gravity of petrol with respect to water.

A16)

Given: V=2 liter = 2 x 10-3m,

W=14N

To find:

1. Specific weight,
2. Density,
3. Specific volume
4. Specific gravity.

1. Specific weight

Specific weight = Mass density x Acceleration due to gravity

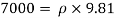
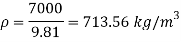
2.     Specific volume (V)

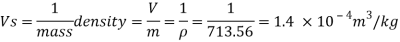
3.     Specific gravity (S)

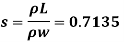
Q17) A 400 ml of certain liquid weight 9N calculate the weight density and specific gravity of the liquid.

A17)

Given:

Volume V= 400 ml-0.4 L=0.4/1000=4x10^-4 m^3

Weight W=9N

To find: Weight density, specific gravity

1. Weight density (Y) =

2.     Specific gravity

Q18) A plate 0.02 mm distance from a fixed plate, moves at 60 cmvs and requires a force of 3 N/m² to maintain this speed. Determine the fluid viscosity between the plates.

A18)

Given: Distance between plates

Dy= 0.02 mm = 0.02 x 10-3 m

Velocity of upper plate u 60 cm/s 0.6 m/s

Change in velocity du=u-0-0.6 m/s.

= Force per unit Area = 3 N/m²

To find: Viscosity

Using Newton's law of viscosity

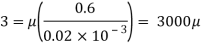
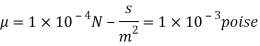
The fluid viscosity between the plates is 1 x 10-3 poise,

Q19) A flat plate of area 2.5 x 10 mm² is pulled with a speed of 0.4m's relative to another plate locate at a distance of 0.15mm from it. Find the force and power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise

A19)

Given:

A=2.5 x 10 mm²=2.5m²,

Du= 0.4m/s dy-0.15mm = 0.15 x 10 m,

=1 poise = 0.1N-s/m

To find: Force, power

Using Newton's law of viscosity:

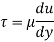
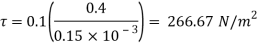
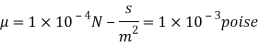
As we known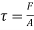

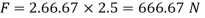
Power required to move the plate at speed 0.4 m/s

= Force x Velocity = 666.67 x 0.4 N-m/

1 N-m/s = 1 Watt

P = 266.67 Watt

Power required moving the plate is 266.67 Watt.

Q20) The space between two square flat parallel plates is filled with oil. Each side of the plate is 720 mm. The thickness of the oil film is 15 mm. The upper plate, which moves at 3 ms requires a force of 120 N to maintain the speed. May 2016. 6 Marks

Determine:

(1) The dynamic viscosity of oil.

(2) The kinematic viscosity of oil if the specific gravity of oil is 0.95

A20)

Square plate of side, a = 720 mm=0.72 m

Thickness of oil film, t = 15 mm= 15 x 10

Velocity of plate v= du= 3m/s

Force F= 120 N

Specific gravity s= 0.95

To find

Mass density,

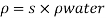
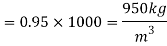
Area of plate,

A= 0.72x0.72 = 0. 5184 m²

Using Newton's law viscosity

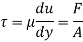
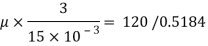
Dynamic viscosity 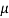= 1.157 N/m²

Kinematic viscosity, v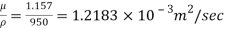

Q21) A body with gravity force of 500 N with a flat surface area 0.2 m slides down a lubricated inclined plane making a 30° angle with the horizontal. For viscosity of 0.1 kg s/m and body speed of 1 m/s. Determine the lubricant film thickness

A21)

Given:

Area A = 0.2 m²

Weight of late W = 500 N

Velocity of plate u = 1 m/sec 0.1kg /m²=0.1 x 9.81 N.s/m² = 0.981 N-s/m²

To find: Thickness of film.

Component of W along the plate W sin 8= 500 sin 30= 250 N

Shear force on the bottom surface of the plate

F = 250N

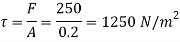
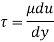
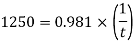
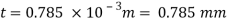
The lubricant film thickness is 0.785 mm

Q22) A rectangular plate 1.2 m x 0.4 m. Weighting 970N slides down a 45° inclined surface at a uniform velocity of 2.25 m/s. If the 2mm gap between the plate and the inclined surface is filled with oil, determine the viscosity of oil.

A22)

Given:

Area A = 12x04 0.48 m²

Weight of plate W =970 N

Velocity of plate u = 2.25 m/sec

Thickness of film t = dy = 2 mm = 2 x 10³ m

To find: Viscosity

Component of W along the plate= W sin

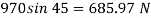
Shear force on the bottom surface of the plate

F= 685.89 N

The viscosity of the liquid is 12.7 poise.

Q23) A skater weighing 1000 N attains a speed of 72 km/hour on ice, average skating area being 10 cm². The dynamic coefficient of friction between the Skater and ice may be taken as 0.015. Determine the average thickness of water. Layer existing between the skater and the skating surface. Viscosity of water at 0°C may be taken 1 x 10 N-s/m².

A23)

Given:

W=1000N,

u = 72 kmph = 72x=20m/sec,

A = 10 cm² = 10 x 10 m², -0.015, 10¹N-s/m²

To find: Average thickness.

Force responsible for motion = Frictional resistance

F = μN=pW

Where N= W

F= 0.015 x 1000 = 15 N

Newton's law of viscosity

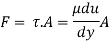
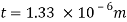
Average thickness of water layer is 1.33 x 10 m

Q24) A body weighing 1000 N slides down at a uniform speed of 1 m/s along a lubricated Inclined plane making 30° angle with the horizontal. The viscosity of lubricant is 0.1 kg/ms and contact area of the body is 0.25 m². Determine the lubricant thickness assuming linear velocity distribution. -June 2011. 6 Marks

A24)

Given:

W= 1000 N,

= 30°

Du = V = 1m/s,

A=0.25 m²

H=0.1 kgm/s 0.1x9.81 Nm/s = 0.981 Nm/s

To find: Lubricant thickness t

Shear force= Weight component along plane

= 1000 sin 30

F = 500 N

Shear stress

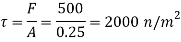
By Newton's law of viscosity

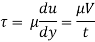
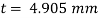
The lubricant thickness is 4.905 mm.

Q25) Calculate the gauge pressure and the absolute pressure within:

(1) a droplet of water 0.3 cm in diameter

(2) a jet of water 0.3 cm in diameter.

Assume the surface tension of water as 0.07 N/m and atmospheric pressure as 101.3 N/m² Dec. 2010, 4 Marks

A25)

Given:

d = 3mm = 3 x 10³ m.

 water = 0.073N/m.

Patm = 101.3 N/m² atm

For droplet and air bubble

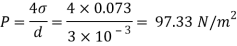
Absolute pressure. (P) = Pgauge + Patm = 97.33 + 101.3 = 198.63 N/m²

For jet

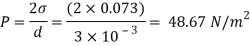
Absolute pressure in jet

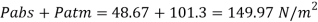
Q26) Determine the diameter of a droplet of water in mm it t pressure inside is to be greater than that outside by 13 Nm². Take a 7.26 10 Nm.

A26)

Given:

P-130 N/m²

= 7.26×10^-2 N/m

For droplet, P

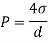
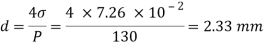
The diameter of a droplet of water is 2.33 mm

Q27) In the surface tension at air water interface is 0.070 Nm what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?

A27)

Given: -

= 0.07 Nm.

D= 001mm= 0.01 = 10 m

An air bubble has only one surface,

The pressure difference between inside and outside of an air bubble is P= 25000N/m2

Q28) Calculate the pressure inside a soap bubble of 50mm diameter. Take surface tension at the soap air interface as 0.1Nm

A28)

Given:

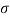= 0.1Nm,

d=50x10^-3  mm

For soup bubble, P

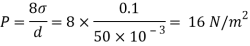
The pressure inside a soup babble is 16 N/m2

Q29) If the surface tension at air water interface is 0.075 N/m, what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?

A29)

Given:

  water = 0.075N/m,

d=0.01mm

An air bubble has only one surface,

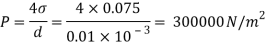
The pressure difference between inside and outside of an air bubble is P=30000N/m2

Q30) What force is necessary to it a thin platinum wire ring of negligible thickness having 5 cm diameter from a water surface? Neglect weight of wire and consider surface tension of water as 0.0725 Nm.

A30)

Given: -

= 0.0725 N/m,

D= 5 cm = 0.05m

Force required to lift a than wire ring

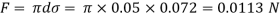
Q31) A 10 mm glass tube is inserted into trough containing mercury. Find the capillary effect when the contact angle is: () 180 and (0) 110 Take surface tension of mercury in contact with air as 0.51 N/m. Dec. 2014.3 Marks

A31)

Given: d = 10 mm= 10 x 10 m,

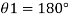
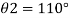
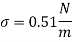
For mercury p=13600 kg/m²

To find: Capillary effect

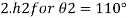
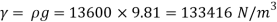
1)     Case 1: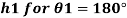

Weight density for mercury

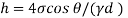
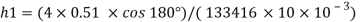
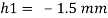
Negative sign indicates capillary depression.

2)     Case 2:

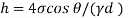
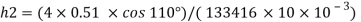
Negative sign indicates capillary depression

Q32) Two wide clean glass plates are held parallel with a gap of 1mm between them. What will be the rise of water level between these plates when dipped in water? Assume surface tension for water as 0.0730 N/m.

A32)

Given:

t=gap=1 mm

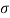=0.073 N/m

For two wide clean glass plates,

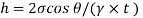
Capillary rise is 14.9 mm.

Q33) A clean tube of internal diameter 3 mm is immerged in a liquid with a coefficient of surface tension 0.48 N/m. Angle of contact of the liquid with the glass can be assumed to be 130%. The density of the liquid is 13600 kg/m". What would be the level of the liquid in the tube relative to the free surface of the liquid outside the tube?

A33)

Given:

d= 3 mm,

= 0.48 N/m

The capillary rise (or depression) is given as

For mercury = 130°. =-0.6428

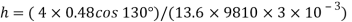
h= - 3. 083 mm

The negative sign indicates that there is capillary depression.

Q34) Find the height through which water rises by capillarity action in a glass tube of 2 mm bore, if the surface tension at the prevailing temperature is 0.0736 N/m. Assume angle of contact of glass with water -0°

A34)

Diameter of glass tube d=2 mm=2x10-3 m

Surface tension=0.0736 N/m

Angle of Contact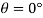

Capillary rise

h= 15 mm

The height by which water rises by capillary is 15 mm.

Q35) A glass tube of internal diameter 0.2 mm is immersed in mercury. The angle of contact of mercury with glass can be taken as 130 W lat will be the level of Hg in the tube relative to the free surface of the liquid outside the tube? Take surface tension of liquid = 0.5 N/m Dec. 2010, 6 Marks

A35)

Given: d= 0.2mm,

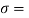0.5 N/m

The capillary rise (or depression) is given as

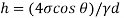
For mercury

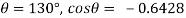
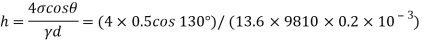
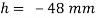
The negative sign indicates that there is capillary depression.

Q36) Determine the minimum size of glass tube that can be used to measure water level, if the capillary rise in the tube is not to exceed 0.25 mm, Take surface tension of water in contact with air as 0.0735 N/m. May 2013, 6 Marks

A36)

Given:

h=0.25 mm,

=0.0735 N/m,

To find: Minimum size of glass tube 'd'.

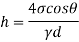
For water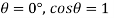

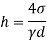
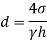
Q37) State the minimum diameter of glass tube to be immersed in water, for which capillarity effects are to be limited up to 2.08mm Take surface tension of water in contact with air as 0.073 N/m.  June 2011; 2 Marks

A37)

Given:

h=298mm,

=0.073 N/m,

for glass plates

To find: Diameter of tube,

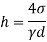
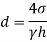
The diameter of glass tube immersed in water is 10 mm.

Q38) Determine the Bulk modulus of elasticity of a liquid, which is compressed in a cylinder from a volume of 0.0125 m³ at 80 N/cm² pressure to a volume of 0.0124 m³ at 150 N/cm² pressure?

A38)

Given:

Initial volume V = 0.0125 m²,

Final volume = 0.0124 m³

DV = Decreases in volume = 0.0125 -0.0124 = 0.0001m³

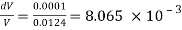
Initial pressure = 80 N/cm2

Final pressure - 150 N/cm

Increases in pressure = 150-80= 70 N/cm = 70 x 10^4 N/m²

Bulk modulus K

Change in pressure/(change volume/ original volume)

The Bulk modulus of elasticity of a liquid is 56.79 x 10^6 N/m2

Q39) Determine the Bulk modulus of elasticity of a liquid, if the pressure of the liquid is increased from 400 Pa to 1200 Pa. The volume of the liquid decreases by 0.15% June 2010, 4 Marks

A39)

Given:

Initial pressure 400 Pa,

Final pressure 1200 Pa,

DV = 0.15% V

Increases in pressure

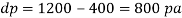
Decreases in volume

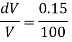
Bulk modulus

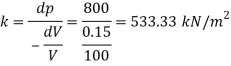
Q40) A cylinder contains a liquid of volume of 0.02 m' at pressure of 700 Pa when compressed to reach a volume of 0.019 m The pressure is increased to 1400 Pa. Find bulk modulus of elasticity Dec. 2011, 2 Marks

A40)

Given:

Initial volume 0.02 m²

Final volume 0.019 m

Change in volume dv=0.02- 0.019 = 1x 10^-3 m^3

Change in pressure dp = 1400-700 = 700 Pa

Bulk modulus k

Q41) If the bulk modulus of elasticity of water is 2.07 x 10° kN/m²:

(1) What is the pressure required to reduce its volume by 2%?

(ii) What will be the change in mass density?

A41)

Given:

K=207 x 10 kN/m²

DV/V= 2%

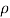for water = 1000 kg/m

To find: dp, d

1)     Pressure required to reduced its volume by 2%

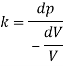
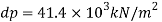
2)     Change in mass density

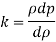
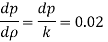
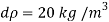
Q42) A pressure of 1.2 M Pascal is applied to 350 liters of liquid, causes a volume reduction of 1.5 liters. Calculate bulk modulus of elasticity for the liquid also find the compressibility.

A42)

Given:

Pressure p= 1.2M,

Pascal = 12x10 N/m².

Volume V 650 liter=  650 x 10³ m.

Reduction in volume dV= 1.5 liter=  1.5 x 10^-3 m3

Bulk modulus of elasticity, K

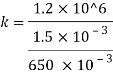
Compressibility

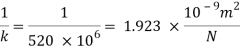
The Bulk modulus of elasticity for the liquid is 520 M Pa and compressibility is 1.923 x 10 m/N.

Q43) At a depth of 5 kilo meters in the ocean the pressure 480 kg/cm Assuming specific weight at the surface as is 1025 kgm and that the average modulus of elasticity is 24 x 10 kg/cm for that pressure range. Calculate:

a) The change in specific volume between the surface and the given depth

b) Specific volume at the given depth and

c) Specific weight at that depth.

A43)

Given:

Pressure dp = 480 kg/cm²

Average modulus of elasticity K = 24 x 10' kg/cm

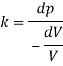
Specific volume of the water at the surface of the ocean,

Specific volume

Specific volume at the depth of 5 km,

Specific weight of water at the depth of 5 km,

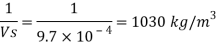
Q44) At a depth of 2 km in an ocean, the pressure is 840 bar. Assume the specific weight at surface as 10,250 N per m² and the average Bulk modulus of elasticity as 2.4 x 10° kN per sq.m. For that pressure range.

1) What will be the change in specific volumes between that at the surface and at that depth?

2) What will be the specific volume at that depth?

3) What will be the specific weight at that depth?

A44)

Given:

P₁ = 840 x 10¹ Pa,

H1, = 2 km = 2000 m.

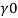 = 10250 N/m²,

K = 2.4 x 10' Pa

Bulk modulus K

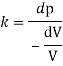
And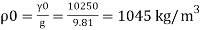

Specific volume

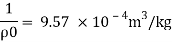
Change in specific volume

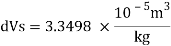
Specific volume at 2 km depth

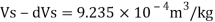
Density at 2 km depth

Specific weight

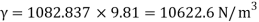
Unit - 1

Unit - 1

Unit - 1

Unit - 1

Basic Concepts and Definition

Q1) Explain distinction between fluid and solid?

A1)

• We have a common, vague idea of ​​difference. Solid is not easily damaged; and the liquid is easily deformed (we can easily move through the air).
• Although it is quite descriptive, this unusual view of the difference between solids and liquids is not very satisfying from a scientific or engineering point of view.
• The obvious difference is based on bow items that are disabled under the action of the external load.
• Fluid is defined as a substance that progressively deforms when subjected to shear stress of any size.
• The shear pressure (force at the per unit area) is created whenever the tangential force is applied to the surface as shown to the individual.
• When solid foods such as iron or other metals are subjected to shear pressure, they will initially be disabled (usually the smallest factor), but they will not continue to degenerate (flow).
• However, common liquids such as water, oil, and air satisfy the definition of liquid — that is, they will flow when they are made by shear pressure.
• Some materials, such as slurries‚ tar, putty, toothpaste, etc., are not easily separated because they will behave stronger if the shear pressure applied is less, but if the pressure exceeds a certain critical amount, the object will move.
• The study of such materials is called Rheology and does not fall into the category of classical fluid mechanics.
• Although the formation of fluid cells is important in the separation of fluids from one another, due to the large number of molecules involved, it is impossible to study the behavior of individual molecules when attempting to explain the function of a liquid at rest or on the move.
• Instead, we demonstrate this behavior by considering the scale, or macroscopic. The amount of interest rate, when the ratio is tested over a small volume containing a large number of molecules.

Q2) Explain density, Specific weight?

A2)

• Quantity (precisely, the size of the volume of a volume; also known as a specific weight), of an object whose weight is the volume of the unit.
• The symbol most commonly used for congestion is ρ (the capital letter of the Greek word rho), although the Latin letter D may also be used. Statistically, quantity is defined as the quantity divided by volume

ρ = m/ v

• Where ρ size, m size, and V is volume. In some cases (for example, in the United States oil and gas industry), overcrowding is freely defined as its weight per unit volume, although this is scientifically incorrect - this number is specifically called a specific weight.

• Pure material overcrowding has the same value as its mass concentration.
• Different materials tend to have different strengths, and congestion can be accompanied by durability, purity and packaging.
• Osmium and iridium are the most well-known substances in normal temperature and pressure conditions.

• To facilitate quantitative comparisons in various unit systems, sometimes incorporating an empty value "related size" or "specific gravity", e.g. A measure of the quantity of an object in that of a normal object, usually water. So the relative density of less than one relative in water means that the object is floating in water.

• The quantity of matter varies with temperature and pressure. These variations are usually small in solids and liquids but very large in gases. Increasing the pressure on an object reduces the volume of the object and thus increases its size.
• Increasing the temperature of an object (with a few exceptions) reduces its size by increasing its volume. In many cases, heating the bottom of the liquid leads to a temperature rise from the bottom to the top, resulting in a decrease in the volume of this warm liquid. This causes it to rise in relation to dense non-heated objects.

• The multiplication of quantities of matter is sometimes called its specific volume, which is a term sometimes used in thermodynamics. Quantity is a powerful structure in that the increase in the number of objects does not increase its size; instead it increases its weight.

Measurement of density

• There are many strategies and levels to measure the size of the materials used. Such techniques include the use of a hydrometer (fluid rehydration method), Hydrostatic balance (fluid and firmness method), an immersive body system (beverage fluid method), pycno meter (fluid and solids), air comparisons pycno meter (solid), oscillating densitometer (liquid), and pour and tap (solid).
• However, each method or procedure measures different types of quantities (e.g. Density, bone size, etc.), so it is necessary to understand the type of density measured and the type of object in question.

Homogeneous material

• The plurality of all the points of an object corresponding to its equality and its magnitude is divided by its total volume. Weight is usually measured in scale or balance; volume can be measured directly (from the geometry of an object) or by liquid transfer. To determine the size of the liquid or gas, hydrometer, dasy meter or Cororiol is flow meter can be used, respectively. Similarly, a hydrostatic weight uses water migration due to the immersed material to determine the size of the object.

Heterogeneous material

• When the body is incompatible, its homosexuality varies between different regions of the object. In that case the congestion around any given area is determined by the calculation of the maximum volume around that area. At the lowest volume limit the density of the non-point object

m = integration v ρ (r)d V

Non compacted material

• In practice, bulk materials such as sugar, sand, or ice contain voids. Many substances exist in nature such as flakes, pellets, or granules.

• Voids are regions that contain something other than imaginary objects. Normally this void is air, but can also contain vacuum, liquid, solid, or a different gas or gas mixture.

• Bulk volume - including an empty fraction - is usually obtained by simple measurement (e g by measuring cup measurement) or by geometry from known sizes.

• Mass divided by the volume of the pile determines the congestion of the pile. This is not the same as volumetric mass.

• To determine the size of the weight of the volume, one must first reduce the volume of the missing portion. Sometimes this can be determined by geometric thinking. Close packaging for equal parts of the empty fraction can be at least 74%.
• It can also be determined by force. Some materials in bulk, however, like sand, have a flexible fraction that depends on how the material is moved or poured. It may be loose or compact, with more or less air space depending on the handling.

• In practice, an empty fraction is not just air, or gas. In the case of sand, it could be water, which would be useful to measure as the empty fraction of sand filled with water - once all the air bubbles have been removed - can be much more flexible than dry sand compared to empty air.

• In the case of non-composite materials, one should also be careful in determining the size of the material sample.
• If the material is under pressure (the frequency of bad air on the surface of the earth) the determination of the weight from the measured sample scale may need to respond to the effects of the stiffness due to the quantity of the empty material, depending on how the measurement is made.
• In the case of dry sand, sand is so thicker than air that the softening effect is often overlooked (less than one thousandth).

• Mass conversion when removing one empty object and another while maintaining a constant volume can be used to measure the empty fraction, if the difference in the size of the two empty objects is reliably known.

SPECIFIC WEIGHT

• A specific weight, also known as a unit weight, is the unit weight of an item.
• The most commonly used value of the Earth's water table is 4 ° C, which is 9.807 k N / m3 or 62.43
• Gravity words, and very unusual weights, are used for relative size. A common symbol of a certain weight is γ, the Greek letter Gamma.

Definition

• The specific weight, γ, of a story is defined as the product of its plurality, ρ, and the common gravitational force, g: Gamma = ρ g
• Quantity of matter is defined as quantity by unit volume, typically measured in kg / m3. Gravity is usually faster due to gravity, usually given in m / s2, and on Earth it is generally considered to be 9.81 m / s2.
• Unlike quantity, a certain weight is not a fixed asset. Depending on the speed of gravity, it varies from place to place. Pressure can also affect values, depending on the bulk modulus of the object, but often, at moderate pressure, it has a less significant effect than other factors.

Q3) Explain specific gravity?

A3)

• The relative quantity or gravitational force is a measure of the size (volume of a unit volume) of an object in the quantity of a given object.
• The gravitational force of the liquid is almost always measured in relation to the water obtained (at 4 ° C or 39.2 ° F); for gases, the reference is air at room temperature (20 ° C or 68 ° F). The term "relative congestion" is often popular in scientific practice.

• If the density of an object is less than 1 it means that it is more dense than the reference; if it is greater than 1 then it is thicker than the reference.
• If the relative size is 1 exactly the stiffness is equal; that is, equal amounts of these two objects have the same weight. If the reference is water, then an object with a relative mass (or certain gravitational force) less than 1 will float in the water.
• For example, an ice cube, with a relative weight of about 0.91, floats. An object with a relative weight greater than 1 will sink.

• Temperature and pressure should be specified on both the sample and the reference. The pressure is approximately 1 atm (101.325 kPa). When not, it is very common to specify the exact size. Sample and reference temperatures vary from industry to industry.
• In British brewing practice, gravity, as described above, increased by 1000. Certain gravity is widely used in the industry as an easy way to obtain information about the complexity of solutions for various substances such as brines, sugar solutions (syrups, juices, honeys, brewers wort, must, etc.) and acids.

Uses

• The quantity associated with it can help to measure the maturity of a liquid or a gas, or determine the density of an unknown substance from a known congestion in another. Related quantities are often used by geologists and mineralogists to help determine the mineral content of a rock or other sample.
• Gemologists use it as an aid in the identification of gemstones. Water is preferred as a reference because measurements are easy to make in the field (see below for examples of measuring methods).

• As the basic application of industrial quantity measurements in the industry the determination of the focus of objects is a powerful solution and this finding in the RD vs concentration tables is very important for the analyst to enter the table in the correct way for the related quantities.
• For example, in the brewing industry, the Plato table, which calculates the concentration of sucrose in large quantities against real RD, initially (20 ° C / 4 ° C) based on the weight estimates of sucrose solutions made at laboratory temperatures (20 ° C) but with reference to positioning of water at 4 ° C very close to temperatures where the water has its maximum H (H) magnitude 2O) equal to 0.999972 g / cm3 (or 62.43 lb · ft - 3).
• The ASBC table used today in North America, when based on Plato's original table is the apparent average size of (20 ° C / 20 ° C) on the IPTS-68 scale where the water level is 0.9982071 g / cm3. In sugar, soft drinks, honey, fruit juice and sucrose-related industries the mass extraction is taken from this SG-using activity (17.5 ° C / 17.5 ° C). As a final example, British RD units are based on a reference temperature with a sample of 60 ° F and thus (15.56 ° C / 15.56 ° C).

Q4) Explain kinematic and dynamic viscosity?

A4)

Dynamic Viscosity

Absolute viscosity - the coefficient of total viscosity - is the measure of internal resistance. Dynamic (absolute) viscosity is the tangential force at each unit area required to move one horizontal plane in relation to another plane - by unit velocity - while maintaining unit distance outside the fluid.

Shave pressure between layers of fluid in straight lines can be defined by Newtonian fluid as

Liquid - viscosity and velocity profile

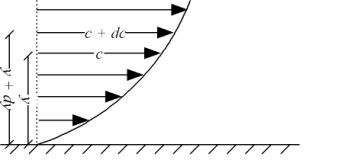
Fig no 1 Dynamic and kinematic viscosity

Shear depression can be shown

τ = μ dc / d y

   = μγ.                                  ........   (1)

Where

τ = cutting pressure on liquid (N / m2)

μ = strong viscosity of liquid (N s / m2)

d c = unit velocity (m / s)

d y = unit distance between layers (m)

γ = dc / d y = shear rate (s-1)

Equation (1) is known as the Newtons Law of Friction.

(1) Can be rearranged to reflect Dynamic viscosity as

μ = τ dy / dc

      = τ / γ.                                     .......... . (1b)

• In the SI system the dynamic viscosity units are N s / m2, Pa s or kg / (m s) - where

1 Pa s = 1 N s / m2 = 1 kg / (m s) = 0.67197 lbm / (ft s) = 0.67197 slug / (ft s) = 0.02089 lbf s / ft2

• Strong viscosity can also be expressed in the metric CGS system (centimeter-gram-second) such as g / (cm s), dyne s / cm2 or poise (p) where

1 poise = 1 dyne s / cm2 = 1 g / (cm s) = 1/10 Pa s = 1/10 N s / m2

• Effective use Poise is usually very large and the unit is therefore divided by 100 - into a small centipoise (cP) unit - where

1 P = 100 cP

1 cP = 0.01 poise = 0.01 gram per cm second = 0.001 second Pascal = 1 milliPascal second = 0.001 N s / m2

20.2oC (68.4oF) liquids have a perfect viscosity of one - 1 –centiPoise.

Kinematic Viscosity

Kinematic viscosity is a measure of the total viscosity - (or intensity) of a quantity - the amount of non-energy. Kinematic viscosity can be obtained by dividing the total viscosity of the liquid by the amount of fluid mass

ν = μ / ρ                               .................. (2)

Where

ν = kinematic viscosity (m2 / s)

μ = full or strong viscosity (N s / m2)

ρ   = density (kg / m3)

In the SI-system the unit of kinematic viscosity theory is m2 / s - or the most commonly used Stoke (St) where

• 1 St (Stokes) = 10-4 m2 / s = 1 cm2 / s

Stoke comes from the CGS unit program (Centimeter Gram Second Second).

As the Stoke unit is usually divided by 100 into smaller units centi Stoke (c St) - there

• 1 St = 100 c St

• 1 c St (centi Stoke) = 10-6 m2 / s = 1 mm2 / s

• 1 m2 / s = 106 centi Stokes

The gravitational force of 20.2oC (68.4oF) is almost the same, and the kinematic viscosity of 20.2oC (68.4oF) water is designed to operate 1.0 mm2 / s (c Stokes). The most precise water viscosity at 20.2oC (68.4oF) is 1.0038 mm2 / s (c St).

Conversion from full viscosity to kinematic in Imperial units can be shown as

ν = 6.7197 10-4 μ / γ.                           .................... (2a)

Where

ν = kinematic viscosity (ft2 / s)

μ = full or strong viscosity (c P)

γ = specific weight (lb / ft3)

Q5) Explain variation of viscosity with temperature?

A5)

• The viscosity of the fluid is due to two contributing factors, namely the interaction between fluid molecules and the transfer of pressure between molecules. In the case of gases the penetration between molecules is large and therefore the interaction of molecules is small.
• But in terms of liquid the molecules are very close together and as a result there is a great deal of interaction. Thus in liquids, viscosity is mainly due to the interaction of the middle cells, while in gases the viscosity is mainly due to the transfer of molecular pressure.
• The bonding force of the molecule decreases with increasing temperature and therefore with increasing temperature the viscosity of the liquid decreases.

The following formula provided by Poiseuille shows the dependence of the viscosity of the liquid on the heat-

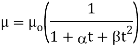
Where, 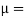Viscosity of the liquid at 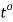C in poise

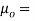Viscosity of the liquid at C in poise

 and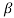 are constant characteristics of the liquid.

For water,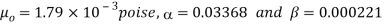

• In the case of gases, as mentioned earlier, the combination of molecules can be ignored viscosity depends largely on the transfer of molecular pressure on the right side to the direction of motion. As the temperature increases the movement of the cells increases that is, there will be a greater transfer of pressure and therefore the viscosity increases. Holman gave the following statement on gas viscosity-
• 

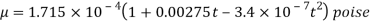
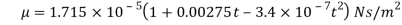
Viscosity of Liquids

Liquid	Viscosity at various temperatures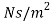
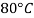Water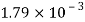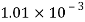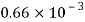
Alcohol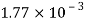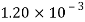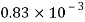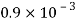
Kerosene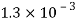
Petrol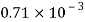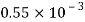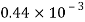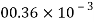

Viscosity of Air at various Temperature

Temperature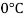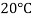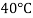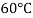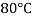
Viscosity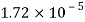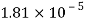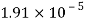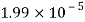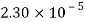

Q6) Explain Newton’s law of viscosity and vapor pressure?

A6)

Newton's viscosity law states that the shear pressure between adjacent water layers is equal to the velocity gradients between these two layers.

The shear pressure ratio and shear ratio are constant, at a given temperature and pressure, and are defined as viscosity or coefficient of viscosity.

Newton’s Law of viscosity,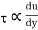

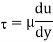
Where,

Viscosity

Shear stress=F/A

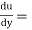Rate of shear deformation

Vapour Pressure

• Vapor pressure (or vapor pressure in British English; see spelling difference) or equilibrium moisture pressure is defined as the pressure exerted by the smoke on the thermodynamic equilibrium and its thick (solid or liquid) phases at a given temperature in a closed system.
• Equilibrium pressure is an indicator of evaporation rate. It is related to the tendency of particles to leak into a liquid (or solid). An object with a high vapor pressure at normal temperatures is often called an invariant.
• The pressure exerted by evaporation over a liquid is known as vapor pressure. As the temperature of a liquid increases, the kinetic energy of its molecules also increases.
• As the kinetic energy of the molecules increases, the number of molecules that evaporates also increases, thus increasing the vapor pressure.

Fig no 2 Vapour pressure

• The vapor pressure of any substance increases with the temperature according to Clausius- Clapeyron's relationship. The atmospheric pressure of boiling liquid (also known as the normal boiling point) is the temperature at which the pressure of the vapor is equal to the atmospheric pressure of the atmosphere.
• With the increasing temperature of that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and to raise the liquid to form vapor bubbles inside the object.
• The formation of a deep bubble in a liquid requires a high temperature due to the high pressure of the liquid, because the pressure of the liquid rises above the atmospheric pressure as the depth increases.
• The most important thing at the deepest depth is the high temperature needed to start bubble formation. The friction of the surface of the bubble wall leads to excessive pressure on very small, initial bubbles.
• The vapor pressure that one part contributes to total pressure in the system is called incomplete pressure. For example, sea air, and filled with water vapor at 20 ° C, has incomplete water pressures of about 2.3 k Pa, 78 k Pa of nitrogen, 21 k Pa of oxygen and 0.9 k Pa of argon, a total of -102.2 k Pa, which forms the basis of the normal atmospheric pressure.

Measurement and uses

• Vapor pressure is measured in standard pressure units. The International System of Units (SI) recognizes pressure as a unit derived from the magnitude of energy in each area and defines pascal (Pa) as its standard unit. One pascal is a newton per square meter (N · m - 2 or kg · m - 1 · s - 2).
• The pulse pressure test measurement is a simple procedure for normal pressures of between 1 and 200 k Pa. The most accurate results are found near the boiling point of objects and large errors result in smaller doses than 1kPa.
• Procedures usually include cleaning the test object, separating it from the container, removing any foreign gas, and then measuring the equilibrium pressure of the gas phase of the object in the container at various temperatures.
• Better accuracy is achieved when care is taken to ensure that everything and its vapor are at a set temperature. This is usually done, such as using an isotonic scope, by inserting the contents of the liquid in a liquid bathtub.
• Very low vapor pressure of solids can be measured using the Knudsen cell method
• According to medical conditions, vapor pressure is sometimes expressed in other units, especially millimeters of mercury (mmHg). This is important for flexible anesthetics, most of which are body fluids, but with very high vapor pressure.

Q7) Explain boiling point and cavitation?

A7)

Boiling Point

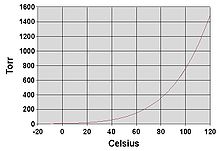
Fig no 3 Boiling point

• The boiling point of a liquid varies depending upon the surrounding environmental pressure. A liquid in a partial vacuum has a lower boiling point than when that liquid is at atmospheric pressure.
• A liquid at high pressure has a higher boiling point than when that liquid is at atmospheric pressure. For example, water boils at 100 °C (212 °F) at sea level, but at 93.4 °C (200.1 °F) at 1,905 meter (6,250 ft) altitude. For a given pressure, different liquids will boil at different temperatures.
• The normal boiling point (also called the atmospheric boiling point or the atmospheric pressure boiling point) of a liquid is the special case in which the vapor pressure of the liquid equals the defined atmospheric pressure at sea level, one atmosphere.
• At that temperature, the vapor pressure of the liquid becomes sufficient to overcome atmospheric pressure and allow bubbles of vapor to form inside the bulk of the liquid. The standard boiling point has been defined by IUPAC since 1982 as the temperature at which boiling occurs under a pressure of one bar.

• The heat of vaporization is the energy required to transform a given quantity (a mol, kg, pound, etc.) of a substance from a liquid into a gas at a given pressure (often atmospheric pressure).

• Liquids may change to a vapor at temperatures below their boiling points through the process of evaporation. Evaporation is a surface phenomenon in which molecules located near the liquid's edge, not contained by enough liquid pressure on that side, escape into the surroundings as vapor.
• On the other hand, boiling is a process in which molecules anywhere in the liquid escape, resulting in the formation of vapor bubbles within the liquid.

• Like all liquids, water evaporates when its vapor pressure reaches its surrounding pressure. Naturally, atmospheric pressure is low at high altitudes and water boils burn low. The boiling water temperature of atmospheric pressure can be compared to the Antoine equation:

Log 10 (P/ 1 Torr) = 8.07131 -[( 1730.63 °c) / (233.426° c + Tb)]

• Or transportation into this temperature explicit form

Tb = [1730.63 °c/ (8.07131 - log 10(P/ 1 Torr))] - 233

Where the temperature Tb is the boiling point in degree Celsius and the pressure P is in Torr

Relation between the normal boiling point and the vapour pressure of liquid

Fig no 4 Log linear Vapour pressure chart

• The steam pressure chart on the right contains graphs of vapor pressure relative to the temperature of the various beverages. As can be seen from the chart, beverages with very high vapor pressure have very low boiling points.
• For example, at any given temperature, methyl chloride has the highest pressure of any gut in the liquid on the chart. It also has the lowest boiling point (-24.2 ° C), at which point the methyl chloride pressure curve (blue line) crosses the horizontal pressure line of one atmosphere of absolute vapor pressure.
• The critical point of the liquid is the very high temperature (and pressure) that it will boil.

Cavitation

• Cavitation is a process in which a decrease in pressure to or under pressure from a liquid vapor leads to the formation of vapor-filled pores in the liquid. When placed under high pressure, these gaps, called "bubbles" or "voids", collapse and can create shocking waves that can damage equipment. These shock waves are strong when they are very close to the inserted bubble, but they quickly become weak as they spread away from the insert

• Cavitation is an important cause of wear in some engineering situations. The collapse of the voids entering near the metal causes cyclic stress through repeated implosion. This causes excess fatigue of the metal which causes a type of wear also called "cavitation". The most common examples of this type of wearable pumping equipment, and bending where there is a sudden change in the flow of fluid. Cavitation is usually divided into two behavioral categories: inertial (or temporal) cavitation and non-inertial cavitation.

• The process by which a void or bubble in a liquid falls rapidly, producing a shock wave, is called an inertial cavitation. Inertial cavitation occurs naturally in strikes of shrimp and pistol shrimps, as well as plant tissue. In man-made objects, it is possible for control valves, pumps, propellers and power inserts.

• Non-inertial cavitation is a process in which a bubble in a fluid is forced to change in size or shape due to some form of energy input, such as an acoustic field. Such cavitation is commonly used in ultrasonic cleaning facilities and can also be seen in pumps, propellers, etc.

• Since shock waves formed by collapsing spaces are strong enough to cause significant damage to parts, cavitation is often undesirable to machinery (although desirable when used intentionally, for example, sterilizing contaminated surgical instruments, dissecting contaminants in water purification systems, emulsify tissue cataract surgery or lithotripsy of kidney stones, or homogenize fluids). Special protection is often avoided in the construction of turbines or propellers, and eliminating cavitation is a major field in the study of fluid dynamics. However, sometimes it helps and does not cause damage when the bubbles fall away from the equipment, such as at high altitudes.

• Cavitation can occur when the local pressure in a liquid reaches a level below the pressure of the liquid vapor at the actual temperature. According to the Bernoulli Equation this can happen if the fluid accelerates to a control valve or to a pump-in area.

• Vaporization itself does not cause damage - damage occurs when the vapor almost immediately after evaporation decreases when the velocity decreases and the pressure increases.

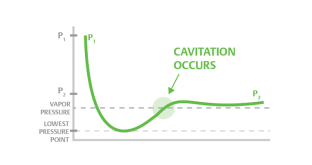
Fig no 5 Cavitation

Avoiding Cavitation

Cavitation can be generally avoided

• Increase the distance (pressure difference) between the actual static pressure on the liquid - and the pressure of the liquid vapor at direct temperature

This can be done by:

• Regenerative engineering components that initiate high speeds and low static pressures
• To increase the total or local pressure in the system
• To reduce the temperature of the liquid

Redesign Components Launch High Speed ​​and Low Static Pressure

Walking and injury can be avoided by using special equipment designed for extreme conditions.

• Situations with large pressure drops can be handled by Multi Stage Control Valves
• Challenging pump conditions with fluid temperatures near vaporization temperature can be treated with special pumps - performance behind other conditions than centrifugal pumps

Increasing total or local pressure in the system

• By increasing the total or local pressure in the system the distance between stationary pressure and vaporization pressure increases and vaporization and cavitation can be avoided.
• The balance between stationary pressure and vaporization pressure - an indication of possible vaporization, is often expressed by Cavitation Number.
• Unfortunately it is not always possible to increase the total static pressure due to system configuration or other limitations. Local static pressure in some parts can increase by lowering (rising) part of the system. Control pipes and pumps should usually be placed at the lowest point of the system to raise the immovable head.
• This is a common solution for boiler feed pumps that receive hot condensate (water up to 100 °C) from condensate receivers in steam plants.

Q8) Explain surface tension?

A8)

• Surface tension is the tendency for the liquid to shrink into the smallest possible area. Facial friction allows insects (e.g. Water arrows), to float and slide on the surface of water without immersion.
• Where fluids combine with air, the resulting incompatibility arises from the greater attraction of liquid molecules to each other (due to bonding) than to air molecules (due to adhesion).
• There are two main processes in play. One is the internal energy of the extra molecules that make the liquid enter. The second is the gravitational force associated with the surface of the membrane. The effect of the net is that the liquid behaves as if its surface was covered with a thick membrane.
• Due to the high attraction of water molecules to each other through the hydrogen bond web, water with a surface elevation (72.8 millinewtons (mN) per meter at 20 ° C) than most other beverages. Facial incompatibility is an important factor in the case of capillarity.
• Extra tension is a measure of the strength in the length of each unit, or the strength in the area of ​​each unit. This is similar, but when referring to the energy in each unit area, it is common to use the term energy energy, which is a common term in the sense that it also applies to solids.
• In science fiction, ground tension is applied either to the pressure of the earth or to higher forces.

Causes

• Due to the relative strength the molecule is pulled evenly on all sides by neighboring chemical molecules, resulting in zero energy. The upper molecules do not have the same molecules on all sides so they are pulled inwards. This creates some internal pressure and forces wet areas to penetrate that small area.
• There is also a surface tension in the liquid-air optical connector that will withstand external forces, due to the interaction of water molecules.
• The gravitational force that works between molecules of the same type is called cohesive force and those that work between molecules of different types are called cohesive forces.
• The balance between fluid mixing and its adhesion to the contents of the container determines the water level, contact angle and position of the meniscus. When cohesion dominates (preferably, the adhesion capacity is less than half the cohesive force) the moisture is low and the meniscus pulls against a straight wall (with respect to mercury in a glass container).
• On the other hand, when adhesion controls (the holding capacity of more than half of the cohesive force) the moisture is high and the same meniscus is concave (as in water in a glass).
• Facial tension is the result of the formation of water droplets. Although easily deformed, water droplets tend to be drawn in an unequal circular motion on the overlapping forces of the upper layer. In the absence of additional energy, droplets of almost all liquid may be round. The rounded shape reduces the "wall friction" required by the upper layer according to Laplace law.
• Another way to look at surface tension is power. A molecule that communicates with a neighbor is in a lower state of energy than it is alone.
• Internal molecules have as many neighbors as possible, but boundary molecules are lost in the neighborhood (compared to internal molecules) and therefore have higher potency.
• In order for a liquid to reduce its energy level, the number of molecules at higher energy limits must be reduced. A reduced number of boundary molecules leads to a much lower surface area.
• As a result of the reduction in area, the area will take on the potential smoothness (statistical evidence that the "smooth" formation reduces the surface area depending on the use of the Euler-Lagrange figure). Since any curvature of the impact shape results in a larger area, there will be higher strength.

Effect of surface tension

Water

Many of the effects of global conflict can be seen in ordinary water:

• Beads of rain water on the surface of the wax, like a leaf. Water adheres weakly to melt and solidify itself, so water collections become droplets. Extra tension gives them their intimate circular shape, because the field has the smallest area over the volume size.

Fig no 6 Water bending on leaf

• The formation of droplets occurs when the weight of the liquid is increased. Flushing (below) indicates that water is attached to the mains for maximum gain until it is extended to an area where ground height can no longer keep the pump connected to the tap. After that it separates and the surface tension creates a partial reduction. When a stream of water flowed out of a tap, the river broke in pieces when it fell. Gravity lightens the stream, and the moisture of the earth drains you into the fields.

Fig no 7 Water dripping from a tap

• The movement of thick objects in water occurs when an object is not soft and its weight is small enough to be carried by forces from the earth's crust. For example, water abusers use ground tension to move on the surface of a lake in the following way. The dehydration of the water rider's leg means that there is no attraction between the leg molecules and the water molecules, so when the leg moves down into the water, the surface tension of the water tries to restore its softness to its flexibility due to the leg. This water behavior pushes the water rider up so that you can stand on the water as long as its weight is small enough for the water to support it. The surface of the water acts like an expanding film: the feet of the insect cause cracks in the surface of the water, increase the surface area and the tendency to decrease the earth's curv (such surface) water pushes the insect's feet upwards.

Fig no 8 Water striders stay atop the liquid because of surface tension

• The separation of oil and water (in this case, water and liquid wax) is caused by a facial imbalance between different drinks. This type of ground tension is called "interface tension", but its chemistry is the same.

Fig no 9 Lava lamp

• Tears of wine the formation of drops and streams along a glass containing an alcoholic beverage. The reason for this is the complex interaction between the different surface tension of water and ethanol; a combination of water-soluble changes by ethanol and ethanol evaporates faster than water.

Fig no 10 Tears of wine

Surfactants

Surface tension is seen in other common causes, especially when surfactants are used to reduce it:

• Soap bubbles have very large areas with very small size. The foam in the clear water is unstable. The addition of surfactants, however, can have a stabilizing effect on bubbles (see Marangoni effect). Note that surfactants actually reduce water resistance by a factor of three or more.
• Emulsions are a type of colloid in which the surface of the earth plays a role. Smaller pieces of oil suspended in pure water will automatically merge into larger masses. But the presence of the surfactant provides a decrease in surface tension, which allows for the stabilization of the minute droplets of oil in most liquids (or vice versa).

Q9) Explain capillarity?

A9)

• Capillary action (sometimes capillarity, capillary motion, capillary effect, or wicking) is the ability of fluid to flow in small areas without assistance, or even to counteract external forces such as gravity.
• The effect can be seen in the formation of fluid between the hairs of the paint brush, in a thin tube, in the smooth material such as paper and cement, in other non-abrasive materials such as sand and carbon fiber, or organic cell.
• It occurs due to intermolecular forces between liquids and solid surrounding environments. If the diameter of the tube is small enough, then a combination of ground incompatibility (caused by coagulation within the liquid) and the ability to adhere between the wall of the liquid and the vessel to form a liquid.
• The first recorded view of the capillary act was by Leonardo da Vinci. A former Galileo student, NiccoloAggiunti, was said to be investigating the carrying of the wheels.
• By 1660, capillary action was still a novelty for Irish chemist Robert Boyle, when he reported that "some Frenchmen wanted to know" realized that when the capillary tube was submerged in water, the water would rise "up into the Pipeline". Boyle then reported on a trial in which he put a capillary tube in red wine and then inserted a tube.
• You have found that the vacuum has no visible effect on the rise of the fluid in the capillary, so the performance of the fluid in the capillary tubes is due to a specific condition different from that which controls the barometers baro meters.
• Some quickly followed Boyle's lead. Some (e.g., HonoreFabri, Jacob Bernoulli) thought that fluid was rising in the capillaries because air could not enter the capillaries as easily as fluid, so air pressure was lower within the capillaries.
• Some (e.g., Isaac Vossius, Giovanni Alfonso Borelli, Louis Carre, Francis Hauksbee, Josia Weitbrecht) thought that liquid particles were attracted to each other and capillary walls.
• Although experimental studies continued through the 18th century, effective treatment of capillary values ​​up to 1805 by two researchers: Thomas Young of the United Kingdom [16] and Pierre-Simon Laplace of France.
• They found the equivalent of the Young - Laplace capillary act. By 1830, German mathematician Carl Friedrich Gauss had determined the parameters of the capillary (i.e., conditions on a solid visual connection). Known as Kelvin's equation.
• German philosopher Franz Ernst Neumann (1798-1895) subsequently decided to collaborate between two non-alcoholic beverages.
• Albert Einstein's first paper, sent to Annalen der Physik in 1900, was astonishing.
• Capillary penetration into media sources shares its powerful equipment through the flow of empty tubes, as both processes are opposed by viscous force.
• As a result, the most common tools used to demonstrate this practice are capillary tube. When the lower end of the glass tube is immersed in fluid, such as water, the concave meniscus forms.
• Adhesion occurs between the fluid and the solid inner wall that pulls the liquid column until there is a sufficient amount of gravity force to overcome these intermolecular forces.
• The length of the contact (edge) between the top of the liquid column and the tube is equal to the width of the intestine, and the weight of the liquid column is equal to the square area of ​​the tube.
• Therefore, a narrow tube will pull the liquid column farther away from the broad bone, provided that the internal water molecules interact sufficiently with the outer ones.

Q10) Explain bulk modulus of elasticity and compressibility?

A10) An elastic modulus (also known as a modulus of elasticity) is a value that measures an object or object to the object of a highly deformed object (i.e., non-permanent) in which pressure is applied. The expandable modulus of the material is defined as the slope of the pressure point in the region of the elastic deformation: Solid material will have a very high modulus. The elastic modulus has the following form:

Delta = stress / strain

Where the pressure is the force that causes the change to be divided by the area in which the force and gravity are used is the rate of change of a particular parameter caused by the distortion in the actual parameter value. Since the difficulty is flawless, the delta will be the same as the units of pressure.

Determining how pressure and complexity will be measured, including indicators, allows for many types of expandable model to be defined. The three main ones are:

1. The Young (E) modulus defines a solid, or tilt, inclination of an object along the axis when opposing forces are used on that axis; defined as a measure of the severity of the stiffness of the stiffness. It is often referred to as the elastic modulus.
2. The shear modulus or stiffness modulus the second parameter of Lame) defines the tendency of an object to shave (change in shape with a fixed volume) when operated by opposing forces; is defined as the shear pressure above the shear type. The shear modulus is part of the viscosity detection.
3. The modulus in the plural (K) defines volumetric stiffness, or the tendency of an object to deform in all indicators when loaded equally in all indicators; is defined as the volumetric pressure over the volumetric mass, and the opposite of the pressure. Modulus in bulk extension of Young's modulus has been in three dimensions.

• Two other extensible methods are Lames first parameter, λ, and P-wave modulus, M, as used in the modulus comparison table given below.

• Homogeneous and isotropic substances (the same in all directions) (solids) have their own (linear) stretchy properties that are fully defined by two stretchable conditions, and one can choose any pair. Given the expansive module, all other expandable methods can be calculated according to the formulas in the table at the bottom of the page.
• Liquids are special because they cannot support shear stress, which means the shear modulus remains zero. This also means that Young's modulus of this group remains a point.

• In some texts, the modulus of elasticity is called constant elastic, and most sizes are called modulus elastic.

COMPRESSIBILITY

• Compression is an asset to be reduced to a minimum by pressure. This material is the result of porosity, and the change in mass occurs from particles that come close together by pressure.
• Liquid pressure is actually a measure of the change in the quantity that will be produced in a liquid by a certain change. Gases, in general, are highly compressed and most liquids have very low pressures.
• The fact that the effects of stress can have a profound effect on the flow of fluid. The study of this flow when changes in quantity and temperature are most important is what is known as compressible flow fluid or gas dynamics.

Q11) Density of liquid is 850 kg/m³. Determine relative density and weight density of the liquid. With reason state whether the liquid will float on water or not

A11)

Gives:

p= 850kg/m'.

P. 1000kg/m (standard value)

To find: Relative density, weight density

Relative density

Weight density

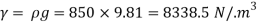
The liquid will float on water because weight density of liquid is less than water.

Q12) On a certain planet a correctly calibrated spring balance shows the weight of a body s 12 N, the mass of which is 4.893 kg. Find the value of gravity on this planet.

A12)

Given:

Weight W= 12 N.

Mass m = 4.893 kg

Weight = Mass x acceleration

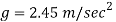
Acceleration due to gravity on a certain planet is 2.45 m/sec.

Q13) What is the specific volume of material with specific gravity 0.87?

A13)

Given:

Specific gravity=0.5,

To find: Specific volume.

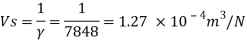
Q14) The specific volume of a certain gas is 0.7m/kg Determine its specific weight and mass density.

A14)

Given:

Specific volume =0.7

To find: Mass density, specific weight

Mass density (p)

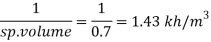
Specific weight (Y)

Q15) Calculate the specific weight, density, specific volume and relative duty of oil which 7 N per liter.

A15)

Given:

Weight W=7N,

Volume V= 1 litre = 10^-3 'm^3

To find:

Specific weight,

Specific volume,

Relative density

Specific weight Y

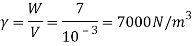
Density

Specific volume (Vs)

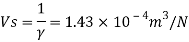
Relative density

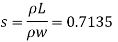
Q16) 2 liter of petrol weighs 14N. Calculate the specific weight, density, specific volume and specific gravity of petrol with respect to water.

A16)

Given: V=2 liter = 2 x 10-3m,

W=14N

To find:

1. Specific weight,
2. Density,
3. Specific volume
4. Specific gravity.

1. Specific weight

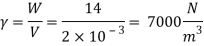
Specific weight = Mass density x Acceleration due to gravity

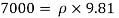
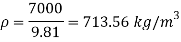
2.     Specific volume (V)

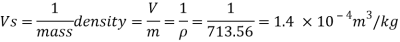
3.     Specific gravity (S)

Q17) A 400 ml of certain liquid weight 9N calculate the weight density and specific gravity of the liquid.

A17)

Given:

Volume V= 400 ml-0.4 L=0.4/1000=4x10^-4 m^3

Weight W=9N

To find: Weight density, specific gravity

1. Weight density (Y) =

2.     Specific gravity

Q18) A plate 0.02 mm distance from a fixed plate, moves at 60 cmvs and requires a force of 3 N/m² to maintain this speed. Determine the fluid viscosity between the plates.

A18)

Given: Distance between plates

Dy= 0.02 mm = 0.02 x 10-3 m

Velocity of upper plate u 60 cm/s 0.6 m/s

Change in velocity du=u-0-0.6 m/s.

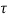= Force per unit Area = 3 N/m²

To find: Viscosity

Using Newton's law of viscosity

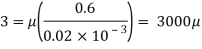
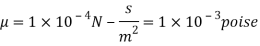
The fluid viscosity between the plates is 1 x 10-3 poise,

Q19) A flat plate of area 2.5 x 10 mm² is pulled with a speed of 0.4m's relative to another plate locate at a distance of 0.15mm from it. Find the force and power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise

A19)

Given:

A=2.5 x 10 mm²=2.5m²,

Du= 0.4m/s dy-0.15mm = 0.15 x 10 m,

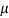=1 poise = 0.1N-s/m

To find: Force, power

Using Newton's law of viscosity:

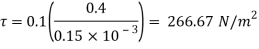
As we known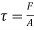

Power required to move the plate at speed 0.4 m/s

= Force x Velocity = 666.67 x 0.4 N-m/

1 N-m/s = 1 Watt

P = 266.67 Watt

Power required moving the plate is 266.67 Watt.

Q20) The space between two square flat parallel plates is filled with oil. Each side of the plate is 720 mm. The thickness of the oil film is 15 mm. The upper plate, which moves at 3 ms requires a force of 120 N to maintain the speed. May 2016. 6 Marks

Determine:

(1) The dynamic viscosity of oil.

(2) The kinematic viscosity of oil if the specific gravity of oil is 0.95

A20)

Square plate of side, a = 720 mm=0.72 m

Thickness of oil film, t = 15 mm= 15 x 10

Velocity of plate v= du= 3m/s

Force F= 120 N

Specific gravity s= 0.95

To find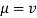

Mass density,

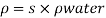
Area of plate,

A= 0.72x0.72 = 0. 5184 m²

Using Newton's law viscosity

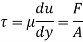
Dynamic viscosity 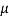= 1.157 N/m²

Kinematic viscosity, v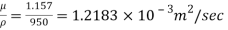

Q21) A body with gravity force of 500 N with a flat surface area 0.2 m slides down a lubricated inclined plane making a 30° angle with the horizontal. For viscosity of 0.1 kg s/m and body speed of 1 m/s. Determine the lubricant film thickness

A21)

Given:

Area A = 0.2 m²

Weight of late W = 500 N

Velocity of plate u = 1 m/sec 0.1kg /m²=0.1 x 9.81 N.s/m² = 0.981 N-s/m²

To find: Thickness of film.

Component of W along the plate W sin 8= 500 sin 30= 250 N

Shear force on the bottom surface of the plate

F = 250N

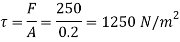
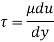
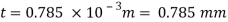
The lubricant film thickness is 0.785 mm

Q22) A rectangular plate 1.2 m x 0.4 m. Weighting 970N slides down a 45° inclined surface at a uniform velocity of 2.25 m/s. If the 2mm gap between the plate and the inclined surface is filled with oil, determine the viscosity of oil.

A22)

Given:

Area A = 12x04 0.48 m²

Weight of plate W =970 N

Velocity of plate u = 2.25 m/sec

Thickness of film t = dy = 2 mm = 2 x 10³ m

To find: Viscosity

Component of W along the plate= W sin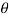

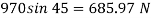
Shear force on the bottom surface of the plate

F= 685.89 N

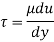
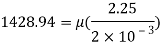
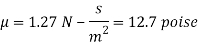
The viscosity of the liquid is 12.7 poise.

Q23) A skater weighing 1000 N attains a speed of 72 km/hour on ice, average skating area being 10 cm². The dynamic coefficient of friction between the Skater and ice may be taken as 0.015. Determine the average thickness of water. Layer existing between the skater and the skating surface. Viscosity of water at 0°C may be taken 1 x 10 N-s/m².

A23)

Given:

W=1000N,

u = 72 kmph = 72x=20m/sec,

A = 10 cm² = 10 x 10 m², -0.015, 10¹N-s/m²

To find: Average thickness.

Force responsible for motion = Frictional resistance

F = μN=pW

Where N= W

F= 0.015 x 1000 = 15 N

Newton's law of viscosity

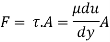
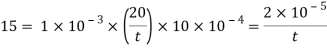
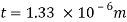
Average thickness of water layer is 1.33 x 10 m

Q24) A body weighing 1000 N slides down at a uniform speed of 1 m/s along a lubricated Inclined plane making 30° angle with the horizontal. The viscosity of lubricant is 0.1 kg/ms and contact area of the body is 0.25 m². Determine the lubricant thickness assuming linear velocity distribution. -June 2011. 6 Marks

A24)

Given:

W= 1000 N,

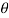= 30°

Du = V = 1m/s,

A=0.25 m²

H=0.1 kgm/s 0.1x9.81 Nm/s = 0.981 Nm/s

To find: Lubricant thickness t

Shear force= Weight component along plane

= 1000 sin 30

F = 500 N

Shear stress

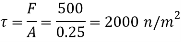
By Newton's law of viscosity

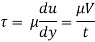
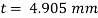
The lubricant thickness is 4.905 mm.

Q25) Calculate the gauge pressure and the absolute pressure within:

(1) a droplet of water 0.3 cm in diameter

(2) a jet of water 0.3 cm in diameter.

Assume the surface tension of water as 0.07 N/m and atmospheric pressure as 101.3 N/m² Dec. 2010, 4 Marks

A25)

Given:

d = 3mm = 3 x 10³ m.

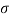 water = 0.073N/m.

Patm = 101.3 N/m² atm

For droplet and air bubble

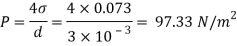
Absolute pressure. (P) = Pgauge + Patm = 97.33 + 101.3 = 198.63 N/m²

For jet

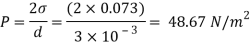
Absolute pressure in jet

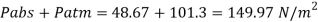
Q26) Determine the diameter of a droplet of water in mm it t pressure inside is to be greater than that outside by 13 Nm². Take a 7.26 10 Nm.

A26)

Given:

P-130 N/m²

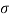= 7.26×10^-2 N/m

For droplet, P

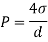
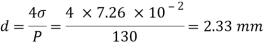
The diameter of a droplet of water is 2.33 mm

Q27) In the surface tension at air water interface is 0.070 Nm what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?

A27)

Given: -

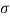= 0.07 Nm.

D= 001mm= 0.01 = 10 m

An air bubble has only one surface,

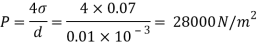
The pressure difference between inside and outside of an air bubble is P= 25000N/m2

Q28) Calculate the pressure inside a soap bubble of 50mm diameter. Take surface tension at the soap air interface as 0.1Nm

A28)

Given:

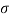= 0.1Nm,

d=50x10^-3  mm

For soup bubble, P

The pressure inside a soup babble is 16 N/m2

Q29) If the surface tension at air water interface is 0.075 N/m, what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?

A29)

Given:

  water = 0.075N/m,

d=0.01mm

An air bubble has only one surface,

The pressure difference between inside and outside of an air bubble is P=30000N/m2

Q30) What force is necessary to it a thin platinum wire ring of negligible thickness having 5 cm diameter from a water surface? Neglect weight of wire and consider surface tension of water as 0.0725 Nm.

A30)

Given: -

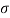= 0.0725 N/m,

D= 5 cm = 0.05m

Force required to lift a than wire ring

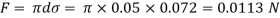
Q31) A 10 mm glass tube is inserted into trough containing mercury. Find the capillary effect when the contact angle is: () 180 and (0) 110 Take surface tension of mercury in contact with air as 0.51 N/m. Dec. 2014.3 Marks

A31)

Given: d = 10 mm= 10 x 10 m,

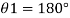
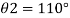
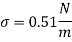
For mercury p=13600 kg/m²

To find: Capillary effect

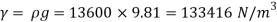
1)     Case 1: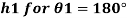

Weight density for mercury

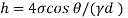
Negative sign indicates capillary depression.

2)     Case 2: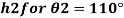

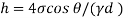
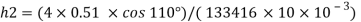
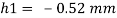
Negative sign indicates capillary depression

Q32) Two wide clean glass plates are held parallel with a gap of 1mm between them. What will be the rise of water level between these plates when dipped in water? Assume surface tension for water as 0.0730 N/m.

A32)

Given:

t=gap=1 mm

=0.073 N/m

For two wide clean glass plates,

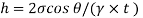
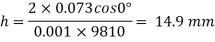
Capillary rise is 14.9 mm.

Q33) A clean tube of internal diameter 3 mm is immerged in a liquid with a coefficient of surface tension 0.48 N/m. Angle of contact of the liquid with the glass can be assumed to be 130%. The density of the liquid is 13600 kg/m". What would be the level of the liquid in the tube relative to the free surface of the liquid outside the tube?

A33)

Given:

d= 3 mm,

= 0.48 N/m

The capillary rise (or depression) is given as

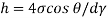
For mercury = 130°. 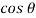=-0.6428

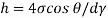
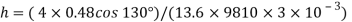
h= - 3. 083 mm

The negative sign indicates that there is capillary depression.

Q34) Find the height through which water rises by capillarity action in a glass tube of 2 mm bore, if the surface tension at the prevailing temperature is 0.0736 N/m. Assume angle of contact of glass with water -0°

A34)

Diameter of glass tube d=2 mm=2x10-3 m

Surface tension=0.0736 N/m

Angle of Contact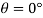

Capillary rise

h= 15 mm

The height by which water rises by capillary is 15 mm.

Q35) A glass tube of internal diameter 0.2 mm is immersed in mercury. The angle of contact of mercury with glass can be taken as 130 W lat will be the level of Hg in the tube relative to the free surface of the liquid outside the tube? Take surface tension of liquid = 0.5 N/m Dec. 2010, 6 Marks

A35)

Given: d= 0.2mm,

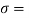0.5 N/m

The capillary rise (or depression) is given as

For mercury

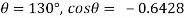
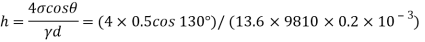
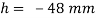
The negative sign indicates that there is capillary depression.

Q36) Determine the minimum size of glass tube that can be used to measure water level, if the capillary rise in the tube is not to exceed 0.25 mm, Take surface tension of water in contact with air as 0.0735 N/m. May 2013, 6 Marks

A36)

Given:

h=0.25 mm,

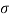=0.0735 N/m,

To find: Minimum size of glass tube 'd'.

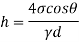
For water

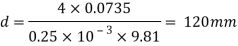
Q37) State the minimum diameter of glass tube to be immersed in water, for which capillarity effects are to be limited up to 2.08mm Take surface tension of water in contact with air as 0.073 N/m.  June 2011; 2 Marks

A37)

Given:

h=298mm,

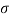=0.073 N/m,

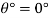for glass plates

To find: Diameter of tube,

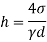
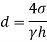
The diameter of glass tube immersed in water is 10 mm.

Q38) Determine the Bulk modulus of elasticity of a liquid, which is compressed in a cylinder from a volume of 0.0125 m³ at 80 N/cm² pressure to a volume of 0.0124 m³ at 150 N/cm² pressure?

A38)

Given:

Initial volume V = 0.0125 m²,

Final volume = 0.0124 m³

DV = Decreases in volume = 0.0125 -0.0124 = 0.0001m³

Initial pressure = 80 N/cm2

Final pressure - 150 N/cm

Increases in pressure = 150-80= 70 N/cm = 70 x 10^4 N/m²

Bulk modulus K

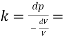Change in pressure/(change volume/ original volume)

The Bulk modulus of elasticity of a liquid is 56.79 x 10^6 N/m2

Q39) Determine the Bulk modulus of elasticity of a liquid, if the pressure of the liquid is increased from 400 Pa to 1200 Pa. The volume of the liquid decreases by 0.15% June 2010, 4 Marks

A39)

Given:

Initial pressure 400 Pa,

Final pressure 1200 Pa,

DV = 0.15% V

Increases in pressure

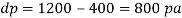
Decreases in volume

Bulk modulus

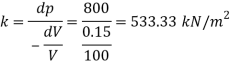
Q40) A cylinder contains a liquid of volume of 0.02 m' at pressure of 700 Pa when compressed to reach a volume of 0.019 m The pressure is increased to 1400 Pa. Find bulk modulus of elasticity Dec. 2011, 2 Marks

A40)

Given:

Initial volume 0.02 m²

Final volume 0.019 m

Change in volume dv=0.02- 0.019 = 1x 10^-3 m^3

Change in pressure dp = 1400-700 = 700 Pa

Bulk modulus k

Q41) If the bulk modulus of elasticity of water is 2.07 x 10° kN/m²:

(1) What is the pressure required to reduce its volume by 2%?

(ii) What will be the change in mass density?

A41)

Given:

K=207 x 10 kN/m²

DV/V= 2%

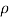for water = 1000 kg/m

To find: dp, d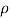

1)     Pressure required to reduced its volume by 2%

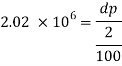
2)     Change in mass density

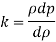
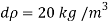
Q42) A pressure of 1.2 M Pascal is applied to 350 liters of liquid, causes a volume reduction of 1.5 liters. Calculate bulk modulus of elasticity for the liquid also find the compressibility.

A42)

Given:

Pressure p= 1.2M,

Pascal = 12x10 N/m².

Volume V 650 liter=  650 x 10³ m.

Reduction in volume dV= 1.5 liter=  1.5 x 10^-3 m3

Bulk modulus of elasticity, K

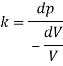
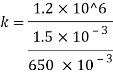
Compressibility

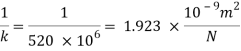
The Bulk modulus of elasticity for the liquid is 520 M Pa and compressibility is 1.923 x 10 m/N.

Q43) At a depth of 5 kilo meters in the ocean the pressure 480 kg/cm Assuming specific weight at the surface as is 1025 kgm and that the average modulus of elasticity is 24 x 10 kg/cm for that pressure range. Calculate:

a) The change in specific volume between the surface and the given depth

b) Specific volume at the given depth and

c) Specific weight at that depth.

A43)

Given:

Pressure dp = 480 kg/cm²

Average modulus of elasticity K = 24 x 10' kg/cm

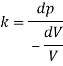
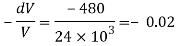
Specific volume of the water at the surface of the ocean,

Specific volume

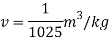
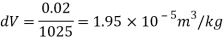
Specific volume at the depth of 5 km,

Specific weight of water at the depth of 5 km,

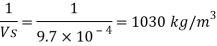
Q44) At a depth of 2 km in an ocean, the pressure is 840 bar. Assume the specific weight at surface as 10,250 N per m² and the average Bulk modulus of elasticity as 2.4 x 10° kN per sq.m. For that pressure range.

1) What will be the change in specific volumes between that at the surface and at that depth?

2) What will be the specific volume at that depth?

3) What will be the specific weight at that depth?

A44)

Given:

P₁ = 840 x 10¹ Pa,

H1, = 2 km = 2000 m.

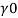 = 10250 N/m²,

K = 2.4 x 10' Pa

Bulk modulus K

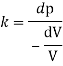
And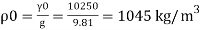

Specific volume

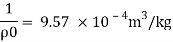
Change in specific volume

Specific volume at 2 km depth

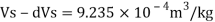
Density at 2 km depth

Specific weight