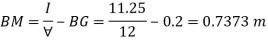Unit - 2
Fluid Statics
Q1) Explain pressure at a point in fluid pressure?
A1)
- Have you ever seen a human tower? Consider the case of the man in the bottom line. You obviously carry a lot more weight than the guy in the first row. It is the same with the pressure of a liquid in a column. In the liquid column, as the depth increases, the pressure increases with it. And why is this pressure increasing? Because as it deepens, the liquid at lower depth should support the excess liquid as well. So to put it bluntly, we can say that
- Fluid pressure is the pressure within the fluid resulting from the weight of the liquid.
Liquid pressure can be calculated using the following relationships.
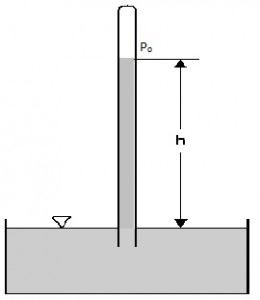
Fig no 1 Fluid measurement
P fluid = P + ρ g h
Where,
P = Pressure on the reference area
P fluid is the pressure at a point in a fluid
ρ is the density of the fluid
g acceleration due to gravity (considering earth g = 9.8 m / s)
h height from the reference point
The volume of this liquid can be calculated by dividing the volume of the liquid by considering the volume of the extracted liquid.
ρ = m / v
Where,
m the size of the liquid
v is the amount of liquid considered
When the liquid is under atmospheric pressure there is a total systemic pressure provided by
P fluid = Po + ρ g h
Where,
Po atmospheric pressure
Conditions for Consideration of fluid pressure:
Water pressure is considered in two cases:
- In open condition or open channel flow
- In a closed case or in a closed ditch
The pressure of the liquid given above is static fluid pressure or hydrostatic pressure. The pressure here is considered to be based on the depth of the liquid only because the pressure generated as a result of the flow of the liquid can be considered minimal. The intensity of static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
Remember that here, liquid refers to anything that has the ability to flow. Therefore, this refers to both beverages and gases.
Factors Affecting Fluid Pressure
There are two factors that affect liquid pressure. These two factors are the depth of the liquid and the quantity of it.
- Depth of fluid: As the depth increases, the pressure released by the fluid increases.
- Liquidity: A liquid as strong as water has a greater pressure than a liquid as light as air. The molecules in the denser fluid are close to each other leading to more collisions in a given area. This results in exertion and increased pressure.
Q2) Explain pascals law?
A2)
The pressure of the liquid given above is the constant pressure of water or hydrostatic pressure. The pressure here is considered to be based solely on the depth of the liquid because the pressure generated by the flow of the liquid can be considered minimal. The size of the static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
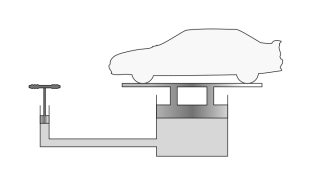
Fig no 2 Pascal's law is the principal behind hydraulic lifting and pressing device

Fig no 3 Pascal law applies for fluid
Pascal's law is defined as
- The change of pressure at any time in the closed liquid at rest is transmitted continuously to all points of the liquid.
- The pressure applied to the liquid in a sealed container is transmitted evenly and is not reduced to all parts of the container and applies with fairness to the closed walls.
- Another explanation: The pressure applied to any part of a closed fluid will be transmitted evenly across all directions of the liquid.
This principle is mathematically defined as:
∆p = ρ g ∆ h
Where
∆p hydrostatic pressure (given by pascals in the SI system), or the difference in pressure in two places within a liquid column, due to the weight of the liquid;
ρ the size of the water (per kilogram per cubic meter in the SI system);
g acceleration due to gravity (usually coastal acceleration due to gravity, meters per second);
∆h the height of the liquid above the measuring point, or the difference in height between two points within a column of water (in meters) .
- An accurate definition of this formula is that the change in pressure between the two heights is due to the weight of the liquid between the heights. Alternatively, the result can be interpreted as a pressure change caused by a potential energy change per unit of liquid due to the presence of a magnetic field. Pressures. Therefore, Pascal's law can be interpreted as any change in pressure applied to any point of fluid being transferred continuously throughout the liquid.
- The formula is a specific mathematical aspect of Navier - Stokes other than the words of inertia and viscosity.
- When the U-tube is filled with water and pistons are fitted at each end, the pressure carried by the left piston will be transferred to all the liquid and below the right piston. (Just four pistons "plugs" can slide freely but inside the tube.)
- The pressure on the left piston against the water will be exactly the same as the water pressure it does when facing the right piston. Suppose the tube on the right is widened and a large area piston is used; for example, the right piston has 50 times the position of the piston on the left.
- When a load of 1 N is placed on the left piston, additional pressure due to the weight of the load is transferred across the liquid and counteracts the larger piston.
- The difference between force and pressure is significant: additional pressure is found throughout the piston area. With an area 50 times larger, there is a 50 times greater force on a larger piston. Therefore, a larger piston will support 50 N load - 50 times the load on a smaller piston.
- Power can be doubled using such a device. One newton input shows the output of 50 newtons. By adding the location of a large piston (or reducing the area of a small piston), the forces can multiply, in fact, by any value. Pascal's foundation supports the operation of a compression machine.
- The hydraulic engine does not break energy savings, because the reduced distance traveled compensates for the increase in energy. When the small piston is removed to the ground by 100 inches, the larger piston will only be raised by fifty inches in this case, or by 2 inches.
- The input power multiplied by the distance transmitted by the small piston is equal to the output power multiplied by the distance transmitted by the large piston; this is just one example of a simple machine that works on the same principle as a machine lever.
- The most common use of Pascal's gas and fluid policy is a vehicle lift that is seen on most service stations (hydraulic jack). The increased air pressure generated by the air compressor is transferred through the air towards the surface of the oil in the underground pool.
- The oil, in turn, exerts pressure on the piston, which lifts the vehicle. The low pressure that exerts the piston lift is almost the same as the air pressure on the car's wheels. Hydraulics are used by modern machines ranging from the smallest to the largest.
- For example, there are pressure pistons on almost all construction equipment where heavy loads are touched.
Q3) Explain pressure variation with temperature and density altitude?
A3)
- When the gas is trapped inside a container with a fixed size (its volume cannot change) and the gas is heated, the particles will gain kinetic energy that will make it faster.
- Gas temperature is equal to the kinetic energy of its molecules. Fast moving particles will collide with container walls more often and with greater force. This causes the strength in the walls of the vessel to increase so the pressure increases.
- When the temperature of a gas is measured in Kelvin's scale, the pressure is equal to the temperature.
In this we can find equality
P1 /T1 = P2 /T2
Where:
P1 is the initial pressure
T1 is the initial temperature
P2 is the final pressure
T2 is the last heat
All temperatures were measured in Kelvin's temperature.
DENSITY ALTITUDE
- Maximum pressure is adjusted by constant temperature. As the temperature rises, the air pressure decreases. In a sense, the height at which a plane “feels” its flight.
- The height of the magnitude is the relative height of the atmospheric conditions where the magnitude of the air can be equal to the magnitude of the air indicated in the viewing area. In other words, the height of the density is the air pressure given as the height above means the sea. The maximum temperature can also be considered as the pressure height adjusted to the ambient temperature.
- Both an increase in temperature and a decrease in atmospheric pressure, and, to a lesser degree, an increase in humidity, will result in an increase in human density. In tropical and subtropical climates, the height of the mass in one area may be much higher than the true elevation.
- For aircraft, maximum altitude is used to test the performance of an airplane aircraft under certain weather conditions. The aviation impacts, as well as the relationship between its indicated airspeed (IAS) and its actual airspeed (TAS), are also subject to changes in wind power. In addition, the force exerted by an aircraft engine is affected by congestion and air conditioning.
Tips for flying at very high altitudes
- I will go in the evening or early morning when temperatures are low.
- Call a local instructor at your destination airport to discuss the flight arrangements at that airport.
- Before taking off for a high-end flight, be aware that your flight is taking off more efficiently with professional hits. Most planes do, but the results are varied and that the first note of the layers can add more drag than lift.
- Make sure the weight of the plane is less than 90 percent of the total weight.
- Do not fill tanks at the top (see previous tip).
- Fly short legs and make another fat stand (a suggestion that is hard to accept, but results in a less pleasant departure).
- Be prepared to take one passenger to the airport with the lowest possible traffic, then return to another. If you are unsure of the circumstances, fly around the pattern once alone without baggage to check the performance of your plane.
- Have an 80% speeding departure from the road area, or have an abortion. That means having 48 IAS knots in Cessna 172 in the middle.
Q4) Explain piezometer and u tube mano meter?
A4)
PIEZOMETER
- A piezometer is the simplest form of manometer which can be used for measuring moderate pressures of liquids.
- It consists of a glass tube inserted in the wall of a vessel or of a pipe, containing liquid whose pressure is to be measured.
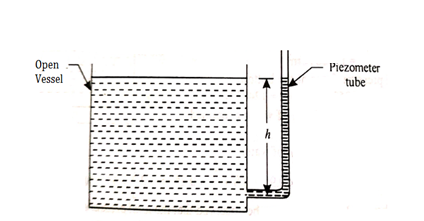
Fig no 4 Piezometer tube fitted to open vessel

Fig no 5 Piezometer tube fitted to a closed pipe
- The tube extends vertically upward to such a height that liquid can freely rise in it without overflowing.
- The pressure at any point in the liquid is indicated by the height of the liquid in the tube above that point, which can be read on the scale attached to it.
- Thus if w is the specific weight of the liquid, then the pressure at point A(p) is given by p = wh
- A piezometer tube is not suitable or measuring negative pressure; as in such a case the air will enter in pipe through the tube.
U-TUBE MANOMETER
- Piezometer cannot be employed when large pressures in the lighter liquids are to be measured, since this would require very long tubes, which cannot be handled conveniently.
- Further more gas pressures cannot be measured by piezometer because a gas forms no free atmospheric surface.
- These limitations can be overcome by the use of U-tube manometers.
- A U-tube manometer consists of a glass tube but in U-shape, one end of which is connected to a point at which pressure is to be measured and other end remains open to the atmosphere as shown in fig.
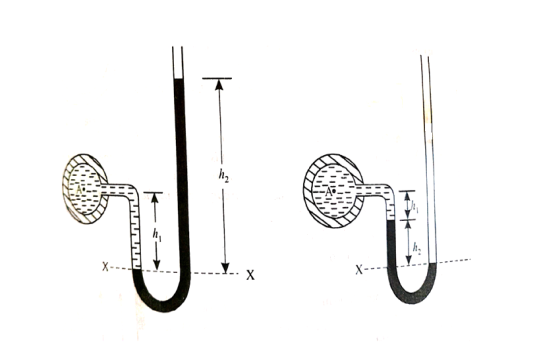
(a). (b)
Fig no 6 Utube manometer
Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)
Let, h1 = height of the light liquid in the left limb above the datum line
h2 = height of the heavy liquid in the right limb above the datum line
h = pressure in pipe, expressed in terms of head
S1 = specific gravity of the light liquid, and
S2 = specific gravity of the heavy liquid
The pressure in the left limb and right limb above the datum line X-X are equal.
Pressure head above X-X line in the left limb = h+h1S1
Pressure head above X-X in the right limb = h2S2
Equating these two pressures, we get
For negative pressure:
Refer to fig(b)
Pressure head above x-x in the left limb=
Pressure head above x-x in the right limb = 0
Equating these two pressures, we get
h + h1S1 + h2S2 = 0 or h = - h2S2 - h1S1
Q5) Explain single column manometer?
A5)
This type of manometer is useful for the measurement of small pressures and is more sensitive than the vertical tube type.
Due to inclination the distance moved by the heavy liquid in the right limb is more.
l = length of the heavy liquid moved in right limb,
Alpha = inclination of right limb horizontal, and
h2 = vertical rise of liquid in right limb from x-x = l sin
h = l sin alpha × S2 - h1S1
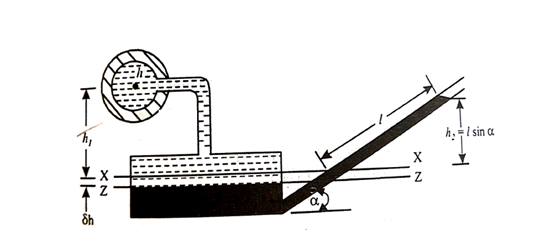
Fig no 7 Single column manometer
Q6) Explain u tube differential manometer?
A6)
A U-tube differential manometer is shown in fig.
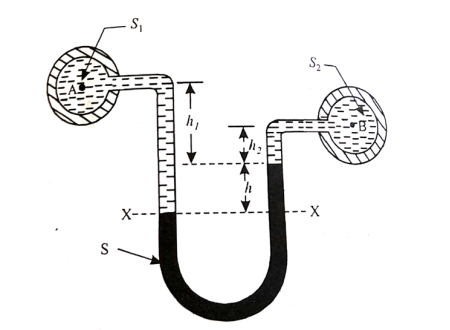
Fig no 8 Utube differential manometer
Let, h = difference of mercury level (heavy liquid) in the U-tube,
h1 = distance of the centre of A, from the mercury level in the left limb
h2 = distance of the centre of B, from the mercury level in the right limb,
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of heavy liquid o mercury
HA = pressure head at A,
HB = pressure head at B
Considering the pressure heads above the datum line x-x, we get
Pressure head in the left limb:
h A + ( h 1 + h ) S1
Pressure head in the right limb:
h B + h 2 × S 2 + h × S
Equating the above pressure heads, we get
h A + ( h1 + h ) S1 = h B + h 2 × S 2 + h× S
( h A - h B ) = h 2 × S 2 + h × S - ( h 1 + h ) S 1
Q7) Explain manometer?
A7)
- A micro manometer can be used - if required in combination with pitot tubes - to measure, measure, measure and calculate velocity and volumetric flow rate. Micro manometers have high accuracy for measuring high-, low- and variability. Observatory Instruments offer different micro manometers, each with a different application.
- One leg of the micro manometer is the source and the other is the inclined tube, which contains a magnifier. The meniscus in the inclined tube is located at a reliable level adjusted by the hairline viewed by the magnifier.
- First of all both the source and the amplifier are the same pressure. The application of pressure at the end of the spring removes the hairline but can be restored to its original position by increasing or lowering the source (mercury sump).
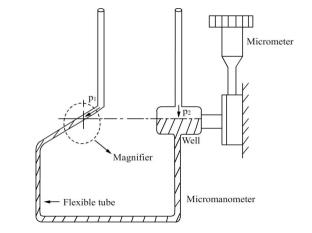
Fig no 9 Micro manometer
Q8) Explain pressure gauge?
A8)
Mechanical Gauges
- The manometers are suitable for comparatively low pressure.
- For high pressures, they become unnecessarily larger even when they are filled with heavy liquids.
- Therefore, for measuring medium and high pressures, we make use of elastic pressure gauges.
- They employ different forms of elastic systems such as tubes, diaphragms or bellows etc. to measure the pressure.
- The elastic deformation of these elements is used to show the effect of pressure. Since these elements are deformed within the elastic limit only, therefore these gauges are sometimes called elastic gauges.
Bourdon tube pressure gauge:
- Bourdon tube pressure gauge is used for measuring high as well as low pressure.
- In this case, the pressure element consists of a metal tube of approximately elliptical cross section.

Fig no 10 Bourdon tube pressure gauge
- This tube is bent in the form of a segment of a circle and responds to pressure changes.
- When one end of the tube which is attached to the gauge case, is connected to the source of pressure, the internal pressure causes the tube to expand, whereby circumferential stress is set up.
- The free end of the tube moves and is in turn connected by suitable levers to a rack, which engages with a small pinion mounted on the same spindle as the pointer.
- Thus the pressure applied to the tube causes the rack and pinion to move.
- The pressure is indicated by the pointer over a dial which can be graduated in a suitable scale.
- The Bourdon tube are generally made of bronze or nickel steel.
- The former is generally used for low pressures and the latter for high pressures.
Diaphragm Gauge:
- This type of gauge employs a metallic disc or diaphragm instead of a bent tube.
- This disc or diaphragm is used for actuating the indicated device.

Fig no 11 Diaphragm gauge
- When pressure is applied on the lower side of the diaphragm it is deflected upward.
- This movement of the diaphragm is transmitted to a rack and pinion.
- The latter is attached to the spindle of needle moving on a graduated dial.
- The dial can again be graduated in a suitable scale.
Vacuum gauge:
- Bourdon gauges discussed earlier can be used to measure vacuum instead of pressure.
- Slight changes in the design are required in this purpose.
- Thus, in this case, the tube be bent inward instead of outward as in pressure gauges.
- Vacuum gauges are graduated in millimeters of mercury below atmospheric pressure.
- In such cases, therefore, absolute pressure in millimeters of mercury is the difference between barometer reading and vacuum gauge reading.
- Vacuum gauges are used to measure the vacuum in the condensers etc. If there is leakage, the vacuum will drop.
Q9) Explain hydrostatic pressure force like horizontal, vertical and inclined surface?
A9)
Fluid Statics
- Fluid Statics interacts with the relaxing fluid while Fluid Dynamics explores the flow fluid.
- Any improved power is caused only by normal pressure i.e., pressure. Such a condition is called hydrostatic condition.
- Fluid Statics is also known as Hydrostatics.
- The static fluid cannot have the shear strength to which it operates, and that any force between the liquid and the boundary must operate in a direct way across the boundary.
- As for the liquid at rest, the factor will be proportional. The total number of energy components in any direction will be zero. The sum of the times the power of an object at any point and should be zero.
- Inside the liquid, the pressure is the same at all points in all directions.
- The pressure on the wall of any ship is toward the wall
- The pressure due to the depth is P = ρgh, and is the same for any specific level of the connected liquid.
Fluid Pressure at a point
- If the liquid is dry, then the force acting on any area or area is unique to that area.
- If the force is present in each area of the same boundary, the pressure is said to be the same
Fig no 12 Hydrostatic force on surface
Pascal's Law of Pressure at a Point
- It states that the pressure or pressure somewhere in the static fluid (liquid rest) is equal in all directions. If the fluid does not move according to Pascal's law,
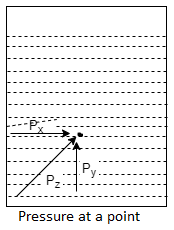
Fig no 13 Pressure at a point
Px = py = pz
Where, px, py and pz pressure point x, y, z respectively.
A typical equation of pressure variability in Static Fluid

Fig no 14 Pressure variability in static fluid
Dp / d s = -  g cos
g cos 
Vertical Variation of pressure in a fluid under gravity

Fig no 15 Vertical Variation of pressure in a fluid
Taking upward as positive, we have
Vertical cylindrical structure of a liquid body = A
Metal size = ρ
The force involved are:
- Force for p1 to A (top) = p1. A
- Force for p2 to A (bottom) = p2. A
- Forcing due to the weight of the material (bottom) = mg
= mass density x volume x g
= ρ.gA.A. (z2 - z1)
Thus in a liquid that is below gravity, the pressure decreases proportionally with the elevation
p2 - p1 = ρgA (z2 - z1)
This is a change in hydrostatic pressure.
Equilibrium of Pressure at Equivalent Static Fluid

Fig no 16 Pressure act on horizontal surface
Horizontal element of cylindrical cross sectional area = A
Metal size = ρ
Left end pressure = pl
Right end pressure = pr
Equally, the total energy in direction x is zero = pl. A = pr. A
Pl = pr
Therefore, the pressure in the horizontal direction does not change.

Fig no 17 Pressure in horizontal direction
As we know, P1 = pr

Therefore, the pressure at two equal levels is the same.
Total Hydrostatic Force in the Facial Area
- On the surface of a liquid plane submerged in a liquid, or in the airplane inside a gas chamber, or in another part of the aircraft under the same hydrostatic pressure, the total hydrostatic power is given by
F = p. A
Where p is the same pressure and A is the area.
- Generally, the total hydrostatic pressure in any aircraft area is equal to the local product output and the unit pressure at its center of gravity.
F = pcg. A
When the pcg pressure is in the center of gravity.
- To get the same free liquid at rest, the number can be displayed according to the unit weight γ of the liquid.
F = γh'A
Where h 'is the depth of the liquid above the centroid of the immersed area.
Q10) Explain buoyancy stability of floating bodies?
A10)
- Whenever a body is immersed wholly or partially in a fluid it is subjected to an upward force which tends to lift it up.
- The tendency for an immersed body to be lifted up in the fluid due to an upward force opposite to action of gravity is known as buoyancy.
- The force tending to lift up the body under such conditions is known as buoyant force or force of buoyancy.
- The magnitude of the buoyant force can be determined by Archimedes principle which states as follows:
- When a body is immersed in a fluid either wholly or partially it is buoyed or lifted up by a force which is equal to the weight of fluid displaced by the body.
Centre of Buoyancy
- The point of application of the force of buoyancy on the body is known as the center of buoyancy. It is always the center of gravity of the volume of fluid displaced.
Equilibrium of floating and submerged bodies
Stability of floating Body:
The stability of a floating body is determined from the position of Meta-centre (M).
a). Stable Equilibrium
- If the point M is above G, the floating body will be in stable equilibrium as shown in Fig.
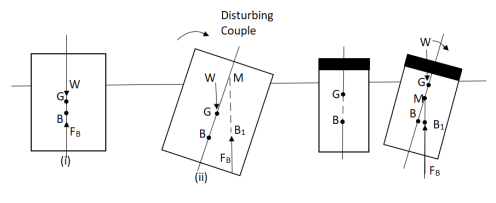
M is above G ( stable equilibrium ). M is below G ( unstable equilibrium )
Fig no 18 Stability of floating bodies
- If a slight angular displacement is given to the floating body in the clockwise direction, the center of buoyancy shifts from B to B1, such that the vertical line through B1 cuts at M.
- Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anti-clockwise direction and thus bringing the floating body in the original position.
b. Unstable Equilibrium:
- If the point M is below G, the floating body will be in unstable equilibrium as shown in fig.
- The disturbing couple is acting in the clockwise direction.
- The couple due to buoyant force FB and W is also acting in clock direction and thus overturning the floating body.
c. Neutral Equilibrium:
- If the point M is at the center of gravity of the body. The floating body will be in neutral equilibrium.
Stability of submerged Body:
- The position of center of gravity ¢er of buoyancy in case of a completely submerged body are fixed.
- Weight W acting vertically downward through G, while the buoyant force FB is acting vertical up through B.
Stable equilibrium :
When W = FB& point B is above G, the body is said to be in stable equilibrium.
Unstable Equilibrium :
If W = FB , but center of buoyancy B is below the center of gravity G, the body is in unstable equilibrium.
Neutral Equilibrium :
If W = FB & point B & G are at the same point, the body is said to be in neutral equilibrium.
Q11) Barometric reading at a place is 75 cm of Hg. Express the pressure intensity of 10 N per cm² is:
(1) m of water
(2) mm of mercury
(3) KN.m^2 abs
A11)
Given:

 = 10 N/cm² = 100 kN/m².
= 10 N/cm² = 100 kN/m².
(i) In m of water,

(ii) In mm of mercury
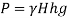
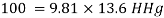

(iii) In kN/m absolute,
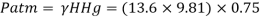

Absolute pressure,

Q12) A gauge on suction side of pump shows a negative pressure of 0.285 bar. Express this pressure in terms of
1. Pressure intensity kPa
2. N/m absolute
3. m of water gauge
4. m of oil (S0.85) absolute
5. Cm of mercury gauge.
Take atmospheric pressure as 76cm of mercury and relative density of mercury as 13.6.
A12)
1 bar = 10'^5 Pa
Gauge vacuum reading
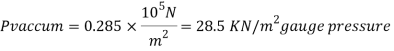
Absolute pressure

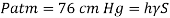
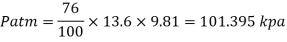
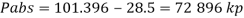
Equivalent head of water (gauge)
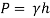
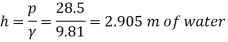
Equivalent head of oil (absolute)
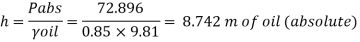
Head of mercury (gauge)

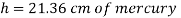
Q13) A cylinder contains a fluid at a gauge pressure of 350kPa. Express the pressure in terms of the column height of (a) water (o 1000kg/m) (b) Hg (S= 13.6). What would be absolute pressure in the cylinder if the atmospheric pressure is 101.3kPa?
A13)
Given:
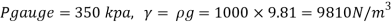
(a) Pressure in term column head of water,
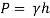

(b) Pressure head in terms of Hg

(c) Absolute Pressure
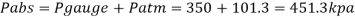
Q14) Mass density of a liquid varies as p = (1000+ 0.008 h). Where 'h' is depth (m) below free surface of liquid. Determine depth at which gauge pressure would be 100 kPa.
A14)
Given: 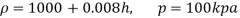
To find: Depth?
Pressure at any point
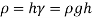
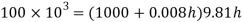
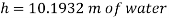
Q15) Measurements of pressure at the base and top of a mountain are 74cm and 60cm of mercury respectively. Workout the height of mountain if air has specific weight 11.97 N/m²
A15)
Pressure at top

Pressure at bottom
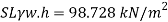


Q16) A piezo meter tube is fitted to a tank containing water at a point 600 mm above the tank. The liquid in the manometer is carbon bi Sulphide having a specific gravity of 1.9. Find the height of the free water surface above the bottom of the tank if the piezo meter reading 700 mm. Find also the pressure intensity at the bottom of the tank. Dec. 2005, 4 Marks
A16)
Pressure at end of piezometer
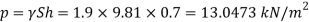
Height of water above point A
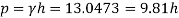
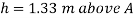
Height of free surface above bottom of tank
H = h +0.6
= 1.33 +0.6 = 1.93m
Pressure at bottom of tank

Q17) A piezometer tube is fitted to a tank containing water at a point 500 mm above the bottom of the tank. The liquid in the manometer is carbon tetrachloride (sp. Gr. 1.6). Find the height of the free water surface above the bottom of the tank if the piezometer reading is 600 mm. Find the pressure intensity at the bottom of the tank.
A17)
For static equilibrium

Pressure in the tank at point A= pressure due to piezometric liquid at A
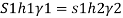
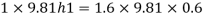

Total height of the free water surface above bottom of tank
h =h₁+0.5 = 0.96 + 0.5 = 1.46 m
Pressure intensity at the bottom of the tank
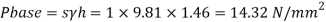
Q18) A simple U-tube manometer is used to measure water pressure in pipe line. The left limb of manometer connected to the pipe and the night limb is open to atmosphere. The mercury level in the left limb is 80mm below the center of the pipe and the level in the right limb in 220mm above the center of the pipe. Calculate the pressure of water in meter and also in km
A18)
Oil
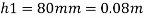

Mercury

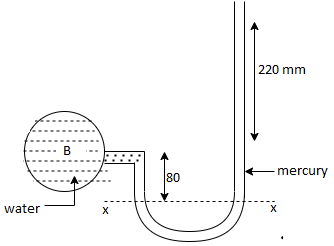
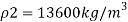
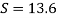
Pressure in the left limb about xx = Pressure in the right limb about x-s

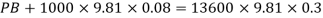


Q19) A U-tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The night limb of the manometer contains mercury and is open to atmosphere. The contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tule 12 cm and the free surface of mercury is in level with the centre of the pipe. It the pressure of water in pipe he is reduced to 9810 N/m². Calculate the new difference in the level of mercury.
A19)

Case I
Given:
h1,=h₂= 12cm=0.12 m.
S2=13.6
Pressure in pipe

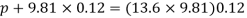

Case II
Since the pressure in the pipe is reduced to 9.81 kN/m² (which is less than 14.83 kN/m²), the mercury in the left limp will be rise. Rise of mercury in the left limb will be equal to the fall of mercury in right limb as the total volume of mercury remains same.
Let x = rise of mercury in left limb= fall in mercury in right limb,
Pressure at new section x₁ - x₁

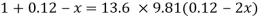

.. New difference of mercury
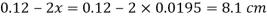
Q20) Fig. P shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer given in the Fig. P. 3.7.15 shows when the vessel is empty. Find the reading of the manometer when the vessel is completely filled with water.
A20)

Case I:
Vessel is empty
Pressure in left limb about x-x= Pressure in right limb about x-x

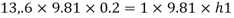
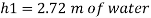
Case II: Vessel is full of water
When pressure is full of water, the pressure in right limb will increase and mercury level will fall by 'y' m, similarly Hg level in left limb will rise by 'y' m
Now consider 7-7 as a datum
Pressure in left limb = Pressure in right limb about z-z
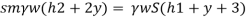
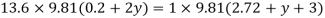
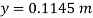
:. Difference of mercury level when the vessel is full of

Q21) A differential manometer is connected at two points A and B of two pipes as shown in Fig. Pipe A contains liquid of specific gravity 1.6, while pipe B contains liquid of specific gravity 0.8. If the pressure at A and B are 11.80 x 10 N/m² and 19.60 x 10 N/m2, find the difference in mercury level in the differential manometer.
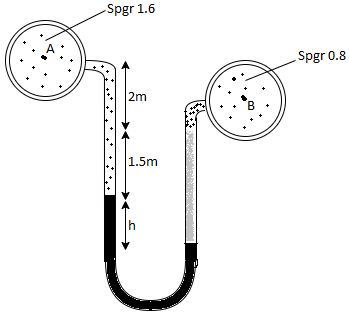
A21)
Pipe A
S₁ = 1.6
PA = 11.8 x 10' N/m² = 118 kN/m² 19.62× 10¹ N/m² = 196.2 kN/m²
h₁ = (2+1,5) = 3.5 h₂ = (1.5 + h)
Pipe B
s2= 0.8
h2= 1.5+h

Pressure in left limb = pressure in right limb PA

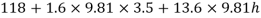

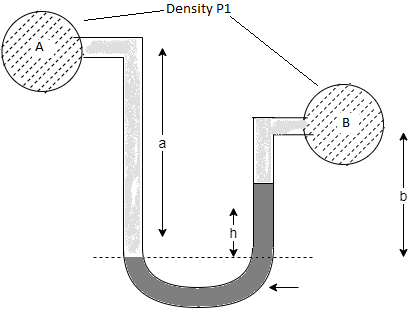
Q22) A U-tube manometer (Fig. P.) measures the pressure difference between two points A and B in a liquid of density PL The U tube contains mercury of density pa. Calculate the difference of pressure between points A and B in a liquid of density p, The u tube contains mercury of density P Calculate the difference of pressure between points A and B if the liquid contain at A is water take a 1.5 m, b=0.75 m and h= 0.50 m.
A22)
Given:
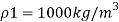


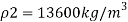
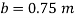
To find :
PA-PB
Pressure in left limb = Pressure in right limb
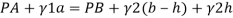
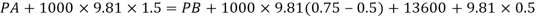

Q23) Liquid of specific gravity 1.0 flows through pipes A and B at positive pressures of 0.5 bar and 0.25 bar respectively. Pipe A is 1.8 m higher than B. What would be the difference in the levels of U-tube manometer connected to A and B, having manometric liquid of specific gravity 13.6 ? Liquid level in the limb attached to A is lower than that in the order.
A23)
Given:
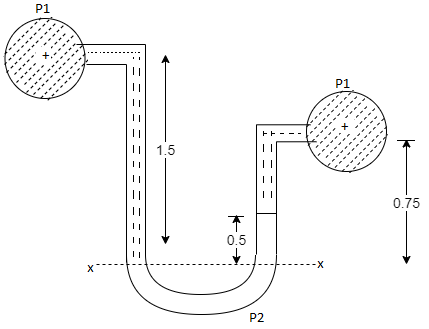
1 1bar = 10^5 N/m²,
2 P=0.5 bar = 50 kN/m².
3 pB= 0.25 bar 25 kN/m²
Balancing the liquid about x-x in left limb and right limb
Pressure in left limb about x-x= Pressure in right limb about x-x


Q24) A pressure gauge, calibrated to read volume of fuel, is used as a fuel gauge. It is connected at the bottom of a fuel tank of area 267 cm². The gauge is calibrated to read maximum volume of 8 liters. If there accumulates 1 cm layer of water in the tank, how much fuel is measured when the gauge shows full scale reading? Assume density of fuel 730 kg/m².
A24)
Given:
Tank base Area A = 267 cm² = 267 x 10 m²
Max. Volume V = 8 liters = 8 x 10¹ m²
Density of fuel p₁ = 730 kg/m

Depth of fuel for maximum volume

Max. Pressure for which gauge is calibrated

Total pressure due to water + Pressure due to fuel
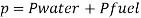
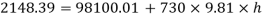

Volume of fuel


For full scale reading, volume of fuel is 7.64 liter
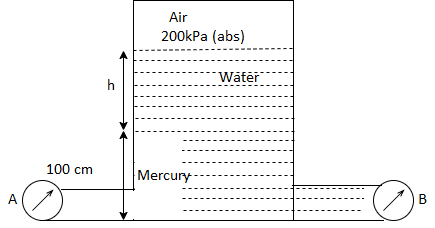
Q25) Gauge A attached at the bottom of a tank shown in Fig. P. 3.7.7 reads 350 kPa (absolute). What is the height 'h' of water? What is the reading of gauge B?
A25)
Given:
P = 350 (absolute)
Pressure due to mercury
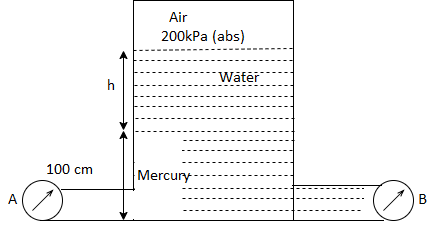
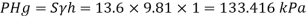
Consider pressure from A up to air
Let 'h' be the height of water
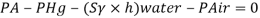


Height of water is 1.69 m
Now consider pressure from air up to gauge B Let P be the gauge pressure at B
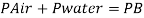

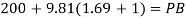
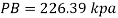
Pressure at B is 226.39 kPa (abs)
Q26) A 6 m deep tank contains 4 m of water and 2 m of oil of relative density 0.8. Determine the pressure at the bottom of the tank.
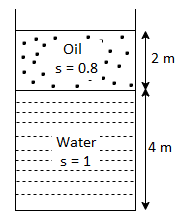
A26)
Specific weight

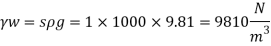
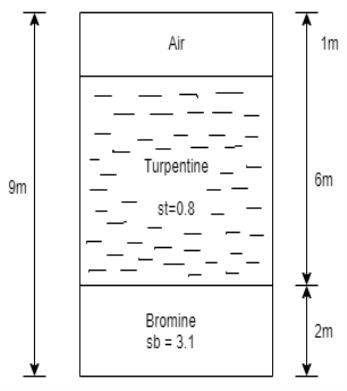
Q27) A closed tank of height 9.0 m is filled with bromine of specific gravity 3.1 to a depth of 2 m and turpentine of specific gravity 0.87 to a depth of 6m. The upper part of the tank contains air under a pressure of 25 kPa (vacuum). Find the absolute pressure at the bottom of the tank in kPa and in cm of mercury Neglect density of air. Consider atmospheric pressure 101.3 kPa.
A27)
Given:
Atmospheric pressure
Patm= 101.3 kpa
Air pressure P=25 kPa (vacuum)
Gauge pressure at bottom of tank
= Air pressure + pressure due to turpentine + pressure due to bromine
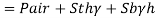


Absolute pressure

Pressure head in term mercury
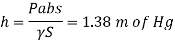
Q28) The tank shown in Fig. P. Is closed at to and contains air at a pressure of P, Calculate the value of P, for the manometer reading as shown in Fig.
A28)
Given:
h₁ = 10 cm = 0.1 m,
h₂ = 150 cm= 15m
h3 = 200+10-150=60 cm=0.6 m
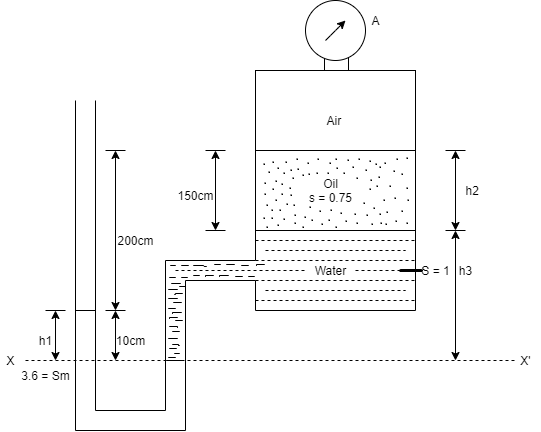
Consider section X-X, balance the fluid about X-X.
Pressure on left limb about XX= Pressure on right limb about X-X
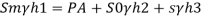
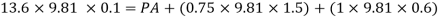
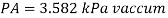
Q29) A vertical rectangular plane surface has width of 1.5 m and depth of 3.0 m. It is placed in water such that the upper edge is 1 m below free water surface. Find the total pressure and the depth of centre of pressure on the rectangular plane.
A29)
Given:
b= 1.5 m,
d = 3.0 m 1m,
s = 1 (water)
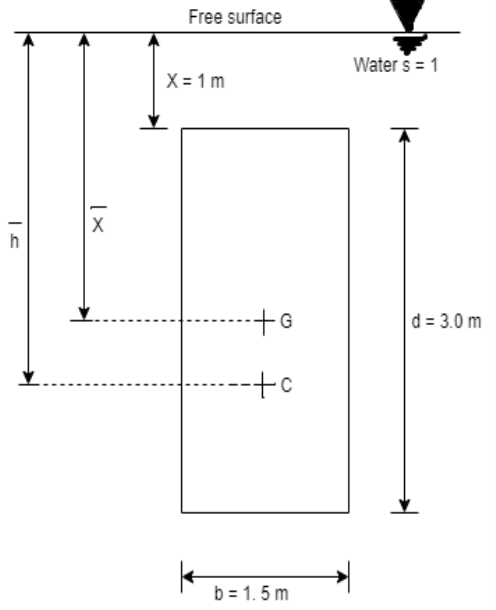
To find: P and h
Area A = b x d=1.5x3=4.5 m²
Distance of centroid of lamina from free surface,
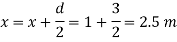
Total of inertia
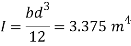
Total pressure,

Centre of pressure,

Q30) A rectangular gate 2 m long and 1.5 m wide lies in a vertical plane with its centre 2.5 m below water surface. Calculate magnitude, direction and location of the total force on the gate.
A30)
Given:
x=2.5m, b = 2m, d=1.5m
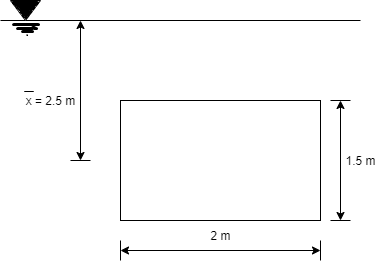
To find
P and h
Moment of inertia

Total pressure

Centre of pressure

Q31) An isosceles triangular plate of base band altitude 'h' meter is immersed vertically in water with its apex below the base. The base is parallel to and vertical depth of 'd below free surface. Prove that the depth of pressure is equal to (h²-4dh+6d²)/ (3d+h)
A31)
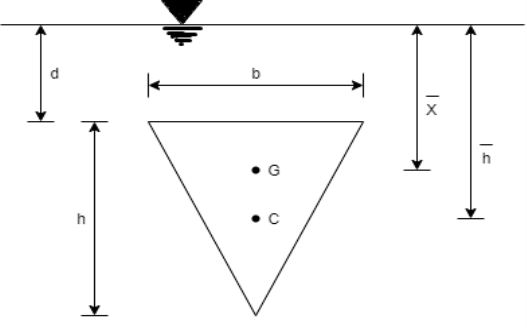
Distance of centroid from free surface

Area of triangle,
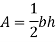
Moment of inertia
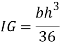
Centre of pressure

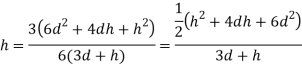
Q32) A circular plate 2.95 m diameter is immersed in water in such a way that its greatest and least depth below the free surface is 4.1 m and 1.6 m respectively. Determine the total pressure on one face of the plate and position of center of pressure.
A32)
Given:
d=2.95 m,
Least depth 1.6 m,
Greatest depth 4.1 m
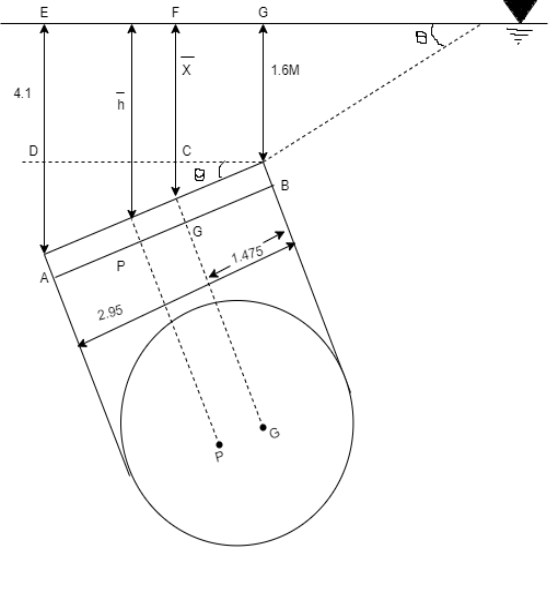
To Find: P and h
Area of plate
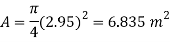
Moment of inertia
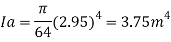
Distance of c. g. Of plate from free surface

1. Total pressure, p

2. Position of center of pressure, h

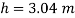
Q33) A square plate 6 m x 6 m is placed in a liquid of specific gravity 0.8 at an angle of 30 with free liquid surface. A square hole 1.5 m in size is cut exactly in the center of the plate. Its greatest and the least depths below the free liquid surface are 4 m and 2 m respectively. Determine the total pressure on one face of the plate and position of center of pressure.
A33)
Given: S=0.8, 0=30°
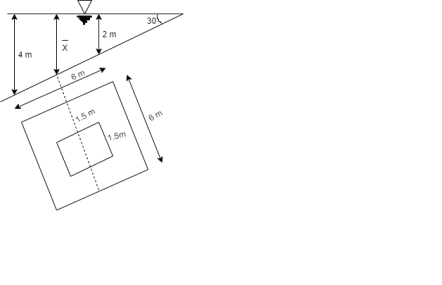
To Find: P and h
Area A=6²-1.5 = 33.75 m²
Position of centroid of lamina from free surface

Moment of inertia,
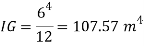
Total pressure,

Q34) A solid cube of sides 0.5 m each is made of material of relative density 0.5. Tho cube floats in a liquid of relative density 0.95 with two of its faces horizontal. Examine its stability.
A34)
Given:

Side a=0.5 m
Relative density 0.5 m
Relative density of cube Sc= 0.5
Relative density of liquid S₁ = 0.95
Weight of cube = Weight of liquid displaced


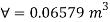
Depth of immersion (h).
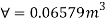
Depth of immersion (h),
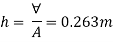
Distance of C.G. From O.

Distance of buoyancy from O.

Now, BG= OG-OB=0.25-0.1315 = 0.1185 m

Metacentric height, BM-BG
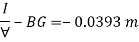
Negative sign of metacentric height indicates that in unstable equilibrium.
Q35) A rectangular pontoon is 5 m long, 3 m wide and 1.20 m high. The depth of immersion of the pontoon is 0.80 m in sea water. If the centre of gravity is 0.6 m above the bottom of the pontoon, determine the metacentric height. The density for sea water = 1025 kg/m².
A35)
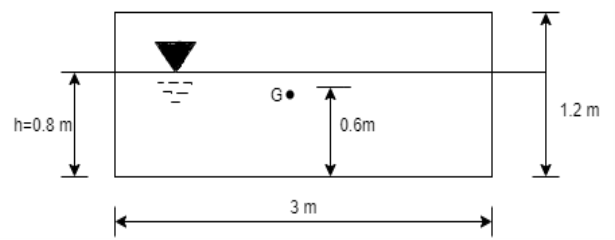
Volume of liquid displaced

Moment of inertia

Metacentric height BM BG=
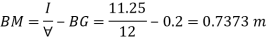
Unit - 2
Fluid Statics
Q1) Explain pressure at a point in fluid pressure?
A1)
- Have you ever seen a human tower? Consider the case of the man in the bottom line. You obviously carry a lot more weight than the guy in the first row. It is the same with the pressure of a liquid in a column. In the liquid column, as the depth increases, the pressure increases with it. And why is this pressure increasing? Because as it deepens, the liquid at lower depth should support the excess liquid as well. So to put it bluntly, we can say that
- Fluid pressure is the pressure within the fluid resulting from the weight of the liquid.
Liquid pressure can be calculated using the following relationships.

Fig no 1 Fluid measurement
P fluid = P + ρ g h
Where,
P = Pressure on the reference area
P fluid is the pressure at a point in a fluid
ρ is the density of the fluid
g acceleration due to gravity (considering earth g = 9.8 m / s)
h height from the reference point
The volume of this liquid can be calculated by dividing the volume of the liquid by considering the volume of the extracted liquid.
ρ = m / v
Where,
m the size of the liquid
v is the amount of liquid considered
When the liquid is under atmospheric pressure there is a total systemic pressure provided by
P fluid = Po + ρ g h
Where,
Po atmospheric pressure
Conditions for Consideration of fluid pressure:
Water pressure is considered in two cases:
- In open condition or open channel flow
- In a closed case or in a closed ditch
The pressure of the liquid given above is static fluid pressure or hydrostatic pressure. The pressure here is considered to be based on the depth of the liquid only because the pressure generated as a result of the flow of the liquid can be considered minimal. The intensity of static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
Remember that here, liquid refers to anything that has the ability to flow. Therefore, this refers to both beverages and gases.
Factors Affecting Fluid Pressure
There are two factors that affect liquid pressure. These two factors are the depth of the liquid and the quantity of it.
- Depth of fluid: As the depth increases, the pressure released by the fluid increases.
- Liquidity: A liquid as strong as water has a greater pressure than a liquid as light as air. The molecules in the denser fluid are close to each other leading to more collisions in a given area. This results in exertion and increased pressure.
Q2) Explain pascals law?
A2)
The pressure of the liquid given above is the constant pressure of water or hydrostatic pressure. The pressure here is considered to be based solely on the depth of the liquid because the pressure generated by the flow of the liquid can be considered minimal. The size of the static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
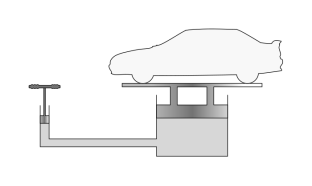
Fig no 2 Pascal's law is the principal behind hydraulic lifting and pressing device
Fig no 3 Pascal law applies for fluid
Pascal's law is defined as
- The change of pressure at any time in the closed liquid at rest is transmitted continuously to all points of the liquid.
- The pressure applied to the liquid in a sealed container is transmitted evenly and is not reduced to all parts of the container and applies with fairness to the closed walls.
- Another explanation: The pressure applied to any part of a closed fluid will be transmitted evenly across all directions of the liquid.
This principle is mathematically defined as:
∆p = ρ g ∆ h
Where
∆p hydrostatic pressure (given by pascals in the SI system), or the difference in pressure in two places within a liquid column, due to the weight of the liquid;
ρ the size of the water (per kilogram per cubic meter in the SI system);
g acceleration due to gravity (usually coastal acceleration due to gravity, meters per second);
∆h the height of the liquid above the measuring point, or the difference in height between two points within a column of water (in meters) .
- An accurate definition of this formula is that the change in pressure between the two heights is due to the weight of the liquid between the heights. Alternatively, the result can be interpreted as a pressure change caused by a potential energy change per unit of liquid due to the presence of a magnetic field. Pressures. Therefore, Pascal's law can be interpreted as any change in pressure applied to any point of fluid being transferred continuously throughout the liquid.
- The formula is a specific mathematical aspect of Navier - Stokes other than the words of inertia and viscosity.
- When the U-tube is filled with water and pistons are fitted at each end, the pressure carried by the left piston will be transferred to all the liquid and below the right piston. (Just four pistons "plugs" can slide freely but inside the tube.)
- The pressure on the left piston against the water will be exactly the same as the water pressure it does when facing the right piston. Suppose the tube on the right is widened and a large area piston is used; for example, the right piston has 50 times the position of the piston on the left.
- When a load of 1 N is placed on the left piston, additional pressure due to the weight of the load is transferred across the liquid and counteracts the larger piston.
- The difference between force and pressure is significant: additional pressure is found throughout the piston area. With an area 50 times larger, there is a 50 times greater force on a larger piston. Therefore, a larger piston will support 50 N load - 50 times the load on a smaller piston.
- Power can be doubled using such a device. One newton input shows the output of 50 newtons. By adding the location of a large piston (or reducing the area of a small piston), the forces can multiply, in fact, by any value. Pascal's foundation supports the operation of a compression machine.
- The hydraulic engine does not break energy savings, because the reduced distance traveled compensates for the increase in energy. When the small piston is removed to the ground by 100 inches, the larger piston will only be raised by fifty inches in this case, or by 2 inches.
- The input power multiplied by the distance transmitted by the small piston is equal to the output power multiplied by the distance transmitted by the large piston; this is just one example of a simple machine that works on the same principle as a machine lever.
- The most common use of Pascal's gas and fluid policy is a vehicle lift that is seen on most service stations (hydraulic jack). The increased air pressure generated by the air compressor is transferred through the air towards the surface of the oil in the underground pool.
- The oil, in turn, exerts pressure on the piston, which lifts the vehicle. The low pressure that exerts the piston lift is almost the same as the air pressure on the car's wheels. Hydraulics are used by modern machines ranging from the smallest to the largest.
- For example, there are pressure pistons on almost all construction equipment where heavy loads are touched.
Q3) Explain pressure variation with temperature and density altitude?
A3)
- When the gas is trapped inside a container with a fixed size (its volume cannot change) and the gas is heated, the particles will gain kinetic energy that will make it faster.
- Gas temperature is equal to the kinetic energy of its molecules. Fast moving particles will collide with container walls more often and with greater force. This causes the strength in the walls of the vessel to increase so the pressure increases.
- When the temperature of a gas is measured in Kelvin's scale, the pressure is equal to the temperature.
In this we can find equality
P1 /T1 = P2 /T2
Where:
P1 is the initial pressure
T1 is the initial temperature
P2 is the final pressure
T2 is the last heat
All temperatures were measured in Kelvin's temperature.
DENSITY ALTITUDE
- Maximum pressure is adjusted by constant temperature. As the temperature rises, the air pressure decreases. In a sense, the height at which a plane “feels” its flight.
- The height of the magnitude is the relative height of the atmospheric conditions where the magnitude of the air can be equal to the magnitude of the air indicated in the viewing area. In other words, the height of the density is the air pressure given as the height above means the sea. The maximum temperature can also be considered as the pressure height adjusted to the ambient temperature.
- Both an increase in temperature and a decrease in atmospheric pressure, and, to a lesser degree, an increase in humidity, will result in an increase in human density. In tropical and subtropical climates, the height of the mass in one area may be much higher than the true elevation.
- For aircraft, maximum altitude is used to test the performance of an airplane aircraft under certain weather conditions. The aviation impacts, as well as the relationship between its indicated airspeed (IAS) and its actual airspeed (TAS), are also subject to changes in wind power. In addition, the force exerted by an aircraft engine is affected by congestion and air conditioning.
Tips for flying at very high altitudes
- I will go in the evening or early morning when temperatures are low.
- Call a local instructor at your destination airport to discuss the flight arrangements at that airport.
- Before taking off for a high-end flight, be aware that your flight is taking off more efficiently with professional hits. Most planes do, but the results are varied and that the first note of the layers can add more drag than lift.
- Make sure the weight of the plane is less than 90 percent of the total weight.
- Do not fill tanks at the top (see previous tip).
- Fly short legs and make another fat stand (a suggestion that is hard to accept, but results in a less pleasant departure).
- Be prepared to take one passenger to the airport with the lowest possible traffic, then return to another. If you are unsure of the circumstances, fly around the pattern once alone without baggage to check the performance of your plane.
- Have an 80% speeding departure from the road area, or have an abortion. That means having 48 IAS knots in Cessna 172 in the middle.
Q4) Explain piezometer and u tube mano meter?
A4)
PIEZOMETER
- A piezometer is the simplest form of manometer which can be used for measuring moderate pressures of liquids.
- It consists of a glass tube inserted in the wall of a vessel or of a pipe, containing liquid whose pressure is to be measured.
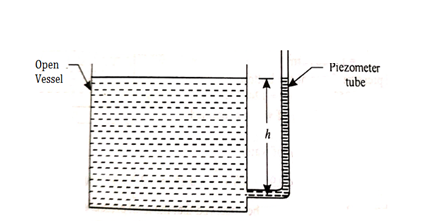
Fig no 4 Piezometer tube fitted to open vessel
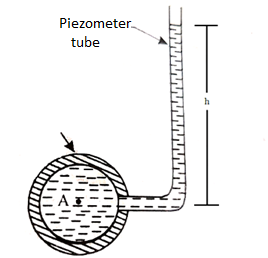
Fig no 5 Piezometer tube fitted to a closed pipe
- The tube extends vertically upward to such a height that liquid can freely rise in it without overflowing.
- The pressure at any point in the liquid is indicated by the height of the liquid in the tube above that point, which can be read on the scale attached to it.
- Thus if w is the specific weight of the liquid, then the pressure at point A(p) is given by p = wh
- A piezometer tube is not suitable or measuring negative pressure; as in such a case the air will enter in pipe through the tube.
U-TUBE MANOMETER
- Piezometer cannot be employed when large pressures in the lighter liquids are to be measured, since this would require very long tubes, which cannot be handled conveniently.
- Further more gas pressures cannot be measured by piezometer because a gas forms no free atmospheric surface.
- These limitations can be overcome by the use of U-tube manometers.
- A U-tube manometer consists of a glass tube but in U-shape, one end of which is connected to a point at which pressure is to be measured and other end remains open to the atmosphere as shown in fig.

(a). (b)
Fig no 6 Utube manometer
Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)
Let, h1 = height of the light liquid in the left limb above the datum line
h2 = height of the heavy liquid in the right limb above the datum line
h = pressure in pipe, expressed in terms of head
S1 = specific gravity of the light liquid, and
S2 = specific gravity of the heavy liquid
The pressure in the left limb and right limb above the datum line X-X are equal.
Pressure head above X-X line in the left limb = h+h1S1
Pressure head above X-X in the right limb = h2S2
Equating these two pressures, we get
For negative pressure:
Refer to fig(b)
Pressure head above x-x in the left limb=
Pressure head above x-x in the right limb = 0
Equating these two pressures, we get
h + h1S1 + h2S2 = 0 or h = - h2S2 - h1S1
Q5) Explain single column manometer?
A5)
This type of manometer is useful for the measurement of small pressures and is more sensitive than the vertical tube type.
Due to inclination the distance moved by the heavy liquid in the right limb is more.
l = length of the heavy liquid moved in right limb,
Alpha = inclination of right limb horizontal, and
h2 = vertical rise of liquid in right limb from x-x = l sin
h = l sin alpha × S2 - h1S1

Fig no 7 Single column manometer
Q6) Explain u tube differential manometer?
A6)
A U-tube differential manometer is shown in fig.
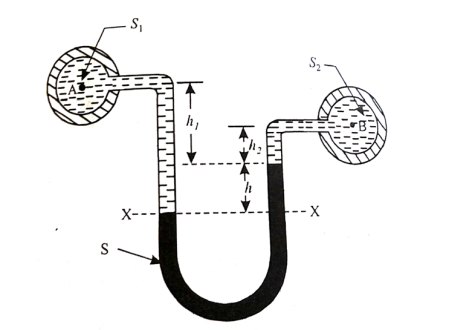
Fig no 8 Utube differential manometer
Let, h = difference of mercury level (heavy liquid) in the U-tube,
h1 = distance of the centre of A, from the mercury level in the left limb
h2 = distance of the centre of B, from the mercury level in the right limb,
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of heavy liquid o mercury
HA = pressure head at A,
HB = pressure head at B
Considering the pressure heads above the datum line x-x, we get
Pressure head in the left limb:
h A + ( h 1 + h ) S1
Pressure head in the right limb:
h B + h 2 × S 2 + h × S
Equating the above pressure heads, we get
h A + ( h1 + h ) S1 = h B + h 2 × S 2 + h× S
( h A - h B ) = h 2 × S 2 + h × S - ( h 1 + h ) S 1
Q7) Explain manometer?
A7)
- A micro manometer can be used - if required in combination with pitot tubes - to measure, measure, measure and calculate velocity and volumetric flow rate. Micro manometers have high accuracy for measuring high-, low- and variability. Observatory Instruments offer different micro manometers, each with a different application.
- One leg of the micro manometer is the source and the other is the inclined tube, which contains a magnifier. The meniscus in the inclined tube is located at a reliable level adjusted by the hairline viewed by the magnifier.
- First of all both the source and the amplifier are the same pressure. The application of pressure at the end of the spring removes the hairline but can be restored to its original position by increasing or lowering the source (mercury sump).

Fig no 9 Micro manometer
Q8) Explain pressure gauge?
A8)
Mechanical Gauges
- The manometers are suitable for comparatively low pressure.
- For high pressures, they become unnecessarily larger even when they are filled with heavy liquids.
- Therefore, for measuring medium and high pressures, we make use of elastic pressure gauges.
- They employ different forms of elastic systems such as tubes, diaphragms or bellows etc. to measure the pressure.
- The elastic deformation of these elements is used to show the effect of pressure. Since these elements are deformed within the elastic limit only, therefore these gauges are sometimes called elastic gauges.
Bourdon tube pressure gauge:
- Bourdon tube pressure gauge is used for measuring high as well as low pressure.
- In this case, the pressure element consists of a metal tube of approximately elliptical cross section.
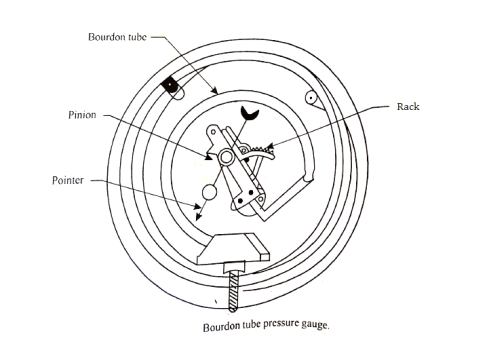
Fig no 10 Bourdon tube pressure gauge
- This tube is bent in the form of a segment of a circle and responds to pressure changes.
- When one end of the tube which is attached to the gauge case, is connected to the source of pressure, the internal pressure causes the tube to expand, whereby circumferential stress is set up.
- The free end of the tube moves and is in turn connected by suitable levers to a rack, which engages with a small pinion mounted on the same spindle as the pointer.
- Thus the pressure applied to the tube causes the rack and pinion to move.
- The pressure is indicated by the pointer over a dial which can be graduated in a suitable scale.
- The Bourdon tube are generally made of bronze or nickel steel.
- The former is generally used for low pressures and the latter for high pressures.
Diaphragm Gauge:
- This type of gauge employs a metallic disc or diaphragm instead of a bent tube.
- This disc or diaphragm is used for actuating the indicated device.
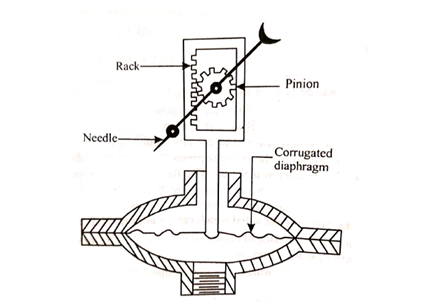
Fig no 11 Diaphragm gauge
- When pressure is applied on the lower side of the diaphragm it is deflected upward.
- This movement of the diaphragm is transmitted to a rack and pinion.
- The latter is attached to the spindle of needle moving on a graduated dial.
- The dial can again be graduated in a suitable scale.
Vacuum gauge:
- Bourdon gauges discussed earlier can be used to measure vacuum instead of pressure.
- Slight changes in the design are required in this purpose.
- Thus, in this case, the tube be bent inward instead of outward as in pressure gauges.
- Vacuum gauges are graduated in millimeters of mercury below atmospheric pressure.
- In such cases, therefore, absolute pressure in millimeters of mercury is the difference between barometer reading and vacuum gauge reading.
- Vacuum gauges are used to measure the vacuum in the condensers etc. If there is leakage, the vacuum will drop.
Q9) Explain hydrostatic pressure force like horizontal, vertical and inclined surface?
A9)
Fluid Statics
- Fluid Statics interacts with the relaxing fluid while Fluid Dynamics explores the flow fluid.
- Any improved power is caused only by normal pressure i.e., pressure. Such a condition is called hydrostatic condition.
- Fluid Statics is also known as Hydrostatics.
- The static fluid cannot have the shear strength to which it operates, and that any force between the liquid and the boundary must operate in a direct way across the boundary.
- As for the liquid at rest, the factor will be proportional. The total number of energy components in any direction will be zero. The sum of the times the power of an object at any point and should be zero.
- Inside the liquid, the pressure is the same at all points in all directions.
- The pressure on the wall of any ship is toward the wall
- The pressure due to the depth is P = ρgh, and is the same for any specific level of the connected liquid.
Fluid Pressure at a point
- If the liquid is dry, then the force acting on any area or area is unique to that area.
- If the force is present in each area of the same boundary, the pressure is said to be the same
Fig no 12 Hydrostatic force on surface
Pascal's Law of Pressure at a Point
- It states that the pressure or pressure somewhere in the static fluid (liquid rest) is equal in all directions. If the fluid does not move according to Pascal's law,
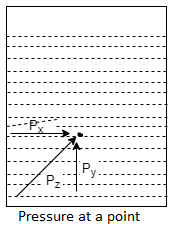
Fig no 13 Pressure at a point
Px = py = pz
Where, px, py and pz pressure point x, y, z respectively.
A typical equation of pressure variability in Static Fluid
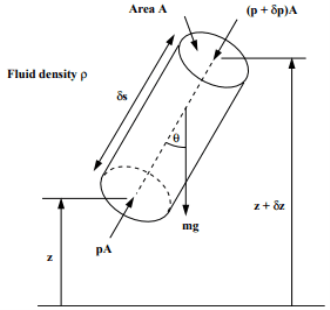
Fig no 14 Pressure variability in static fluid
Dp / d s = -  g cos
g cos 
Vertical Variation of pressure in a fluid under gravity
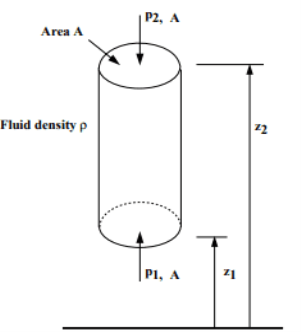
Fig no 15 Vertical Variation of pressure in a fluid
Taking upward as positive, we have
Vertical cylindrical structure of a liquid body = A
Metal size = ρ
The force involved are:
- Force for p1 to A (top) = p1. A
- Force for p2 to A (bottom) = p2. A
- Forcing due to the weight of the material (bottom) = mg
= mass density x volume x g
= ρ.gA.A. (z2 - z1)
Thus in a liquid that is below gravity, the pressure decreases proportionally with the elevation
p2 - p1 = ρgA (z2 - z1)
This is a change in hydrostatic pressure.
Equilibrium of Pressure at Equivalent Static Fluid
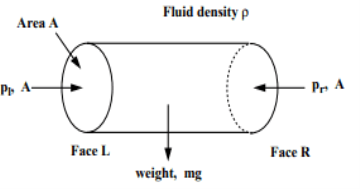
Fig no 16 Pressure act on horizontal surface
Horizontal element of cylindrical cross sectional area = A
Metal size = ρ
Left end pressure = pl
Right end pressure = pr
Equally, the total energy in direction x is zero = pl. A = pr. A
Pl = pr
Therefore, the pressure in the horizontal direction does not change.
Fig no 17 Pressure in horizontal direction
As we know, P1 = pr

Therefore, the pressure at two equal levels is the same.
Total Hydrostatic Force in the Facial Area
- On the surface of a liquid plane submerged in a liquid, or in the airplane inside a gas chamber, or in another part of the aircraft under the same hydrostatic pressure, the total hydrostatic power is given by
F = p. A
Where p is the same pressure and A is the area.
- Generally, the total hydrostatic pressure in any aircraft area is equal to the local product output and the unit pressure at its center of gravity.
F = pcg. A
When the pcg pressure is in the center of gravity.
- To get the same free liquid at rest, the number can be displayed according to the unit weight γ of the liquid.
F = γh'A
Where h 'is the depth of the liquid above the centroid of the immersed area.
Q10) Explain buoyancy stability of floating bodies?
A10)
- Whenever a body is immersed wholly or partially in a fluid it is subjected to an upward force which tends to lift it up.
- The tendency for an immersed body to be lifted up in the fluid due to an upward force opposite to action of gravity is known as buoyancy.
- The force tending to lift up the body under such conditions is known as buoyant force or force of buoyancy.
- The magnitude of the buoyant force can be determined by Archimedes principle which states as follows:
- When a body is immersed in a fluid either wholly or partially it is buoyed or lifted up by a force which is equal to the weight of fluid displaced by the body.
Centre of Buoyancy
- The point of application of the force of buoyancy on the body is known as the center of buoyancy. It is always the center of gravity of the volume of fluid displaced.
Equilibrium of floating and submerged bodies
Stability of floating Body:
The stability of a floating body is determined from the position of Meta-centre (M).
a). Stable Equilibrium
- If the point M is above G, the floating body will be in stable equilibrium as shown in Fig.
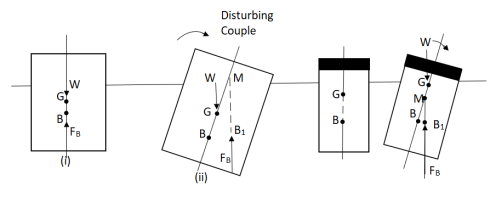
M is above G ( stable equilibrium ). M is below G ( unstable equilibrium )
Fig no 18 Stability of floating bodies
- If a slight angular displacement is given to the floating body in the clockwise direction, the center of buoyancy shifts from B to B1, such that the vertical line through B1 cuts at M.
- Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anti-clockwise direction and thus bringing the floating body in the original position.
b. Unstable Equilibrium:
- If the point M is below G, the floating body will be in unstable equilibrium as shown in fig.
- The disturbing couple is acting in the clockwise direction.
- The couple due to buoyant force FB and W is also acting in clock direction and thus overturning the floating body.
c. Neutral Equilibrium:
- If the point M is at the center of gravity of the body. The floating body will be in neutral equilibrium.
Stability of submerged Body:
- The position of center of gravity ¢er of buoyancy in case of a completely submerged body are fixed.
- Weight W acting vertically downward through G, while the buoyant force FB is acting vertical up through B.
Stable equilibrium :
When W = FB& point B is above G, the body is said to be in stable equilibrium.
Unstable Equilibrium :
If W = FB , but center of buoyancy B is below the center of gravity G, the body is in unstable equilibrium.
Neutral Equilibrium :
If W = FB & point B & G are at the same point, the body is said to be in neutral equilibrium.
Q11) Barometric reading at a place is 75 cm of Hg. Express the pressure intensity of 10 N per cm² is:
(1) m of water
(2) mm of mercury
(3) KN.m^2 abs
A11)
Given:
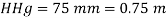
 = 10 N/cm² = 100 kN/m².
= 10 N/cm² = 100 kN/m².
(i) In m of water,
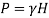
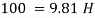
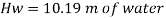
(ii) In mm of mercury

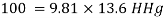
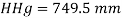
(iii) In kN/m absolute,
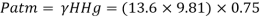

Absolute pressure,

Q12) A gauge on suction side of pump shows a negative pressure of 0.285 bar. Express this pressure in terms of
1. Pressure intensity kPa
2. N/m absolute
3. m of water gauge
4. m of oil (S0.85) absolute
5. Cm of mercury gauge.
Take atmospheric pressure as 76cm of mercury and relative density of mercury as 13.6.
A12)
1 bar = 10'^5 Pa
Gauge vacuum reading
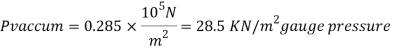
Absolute pressure
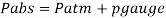
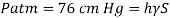

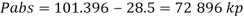
Equivalent head of water (gauge)


Equivalent head of oil (absolute)

Head of mercury (gauge)
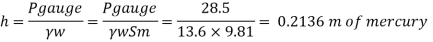

Q13) A cylinder contains a fluid at a gauge pressure of 350kPa. Express the pressure in terms of the column height of (a) water (o 1000kg/m) (b) Hg (S= 13.6). What would be absolute pressure in the cylinder if the atmospheric pressure is 101.3kPa?
A13)
Given:
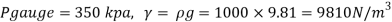
(a) Pressure in term column head of water,


(b) Pressure head in terms of Hg
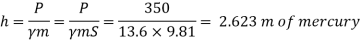
(c) Absolute Pressure
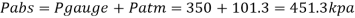
Q14) Mass density of a liquid varies as p = (1000+ 0.008 h). Where 'h' is depth (m) below free surface of liquid. Determine depth at which gauge pressure would be 100 kPa.
A14)
Given: 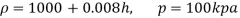
To find: Depth?
Pressure at any point


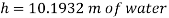
Q15) Measurements of pressure at the base and top of a mountain are 74cm and 60cm of mercury respectively. Workout the height of mountain if air has specific weight 11.97 N/m²
A15)
Pressure at top

Pressure at bottom



Q16) A piezo meter tube is fitted to a tank containing water at a point 600 mm above the tank. The liquid in the manometer is carbon bi Sulphide having a specific gravity of 1.9. Find the height of the free water surface above the bottom of the tank if the piezo meter reading 700 mm. Find also the pressure intensity at the bottom of the tank. Dec. 2005, 4 Marks
A16)
Pressure at end of piezometer
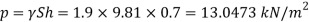
Height of water above point A

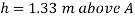
Height of free surface above bottom of tank
H = h +0.6
= 1.33 +0.6 = 1.93m
Pressure at bottom of tank

Q17) A piezometer tube is fitted to a tank containing water at a point 500 mm above the bottom of the tank. The liquid in the manometer is carbon tetrachloride (sp. Gr. 1.6). Find the height of the free water surface above the bottom of the tank if the piezometer reading is 600 mm. Find the pressure intensity at the bottom of the tank.
A17)
For static equilibrium
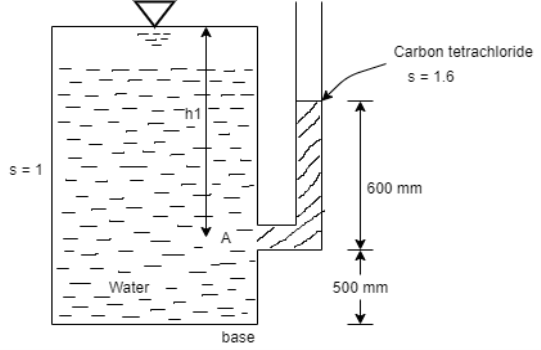
Pressure in the tank at point A= pressure due to piezometric liquid at A
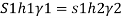


Total height of the free water surface above bottom of tank
h =h₁+0.5 = 0.96 + 0.5 = 1.46 m
Pressure intensity at the bottom of the tank
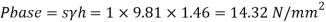
Q18) A simple U-tube manometer is used to measure water pressure in pipe line. The left limb of manometer connected to the pipe and the night limb is open to atmosphere. The mercury level in the left limb is 80mm below the center of the pipe and the level in the right limb in 220mm above the center of the pipe. Calculate the pressure of water in meter and also in km
A18)
Oil

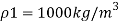
Mercury
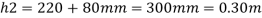

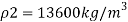

Pressure in the left limb about xx = Pressure in the right limb about x-s
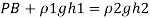
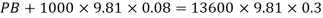
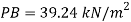
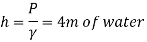
Q19) A U-tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The night limb of the manometer contains mercury and is open to atmosphere. The contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tule 12 cm and the free surface of mercury is in level with the centre of the pipe. It the pressure of water in pipe he is reduced to 9810 N/m². Calculate the new difference in the level of mercury.
A19)
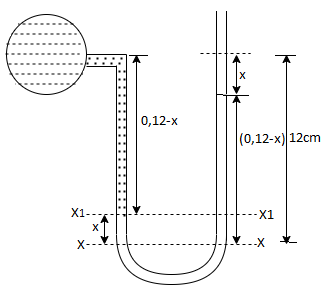
Case I
Given:
h1,=h₂= 12cm=0.12 m.
S2=13.6
Pressure in pipe
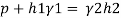
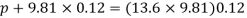

Case II
Since the pressure in the pipe is reduced to 9.81 kN/m² (which is less than 14.83 kN/m²), the mercury in the left limp will be rise. Rise of mercury in the left limb will be equal to the fall of mercury in right limb as the total volume of mercury remains same.
Let x = rise of mercury in left limb= fall in mercury in right limb,
Pressure at new section x₁ - x₁


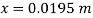
.. New difference of mercury
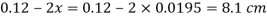
Q20) Fig. P shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer given in the Fig. P. 3.7.15 shows when the vessel is empty. Find the reading of the manometer when the vessel is completely filled with water.
A20)

Case I:
Vessel is empty
Pressure in left limb about x-x= Pressure in right limb about x-x
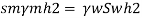
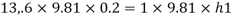
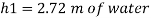
Case II: Vessel is full of water
When pressure is full of water, the pressure in right limb will increase and mercury level will fall by 'y' m, similarly Hg level in left limb will rise by 'y' m
Now consider 7-7 as a datum
Pressure in left limb = Pressure in right limb about z-z
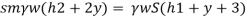
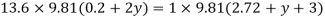
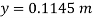
:. Difference of mercury level when the vessel is full of

Q21) A differential manometer is connected at two points A and B of two pipes as shown in Fig. Pipe A contains liquid of specific gravity 1.6, while pipe B contains liquid of specific gravity 0.8. If the pressure at A and B are 11.80 x 10 N/m² and 19.60 x 10 N/m2, find the difference in mercury level in the differential manometer.
A21)
Pipe A
S₁ = 1.6
PA = 11.8 x 10' N/m² = 118 kN/m² 19.62× 10¹ N/m² = 196.2 kN/m²
h₁ = (2+1,5) = 3.5 h₂ = (1.5 + h)
Pipe B
s2= 0.8
h2= 1.5+h
Pressure in left limb = pressure in right limb PA
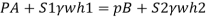
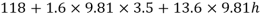
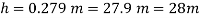
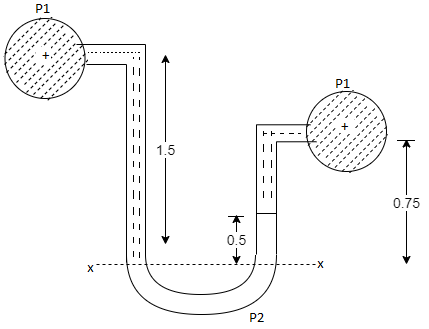
Q22) A U-tube manometer (Fig. P.) measures the pressure difference between two points A and B in a liquid of density PL The U tube contains mercury of density pa. Calculate the difference of pressure between points A and B in a liquid of density p, The u tube contains mercury of density P Calculate the difference of pressure between points A and B if the liquid contain at A is water take a 1.5 m, b=0.75 m and h= 0.50 m.
A22)
Given:

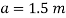
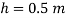
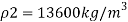

To find :
PA-PB

Pressure in left limb = Pressure in right limb



Q23) Liquid of specific gravity 1.0 flows through pipes A and B at positive pressures of 0.5 bar and 0.25 bar respectively. Pipe A is 1.8 m higher than B. What would be the difference in the levels of U-tube manometer connected to A and B, having manometric liquid of specific gravity 13.6 ? Liquid level in the limb attached to A is lower than that in the order.
A23)
Given:
1 1bar = 10^5 N/m²,
2 P=0.5 bar = 50 kN/m².
3 pB= 0.25 bar 25 kN/m²
Balancing the liquid about x-x in left limb and right limb
Pressure in left limb about x-x= Pressure in right limb about x-x

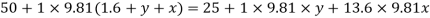
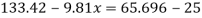
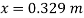
Q24) A pressure gauge, calibrated to read volume of fuel, is used as a fuel gauge. It is connected at the bottom of a fuel tank of area 267 cm². The gauge is calibrated to read maximum volume of 8 liters. If there accumulates 1 cm layer of water in the tank, how much fuel is measured when the gauge shows full scale reading? Assume density of fuel 730 kg/m².
A24)
Given:
Tank base Area A = 267 cm² = 267 x 10 m²
Max. Volume V = 8 liters = 8 x 10¹ m²
Density of fuel p₁ = 730 kg/m
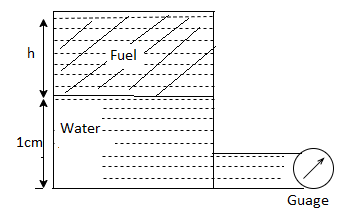
Depth of fuel for maximum volume
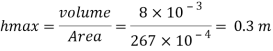
Max. Pressure for which gauge is calibrated

Total pressure due to water + Pressure due to fuel


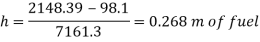
Volume of fuel
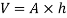
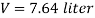
For full scale reading, volume of fuel is 7.64 liter
Q25) Gauge A attached at the bottom of a tank shown in Fig. P. 3.7.7 reads 350 kPa (absolute). What is the height 'h' of water? What is the reading of gauge B?
A25)
Given:
P = 350 (absolute)
Pressure due to mercury
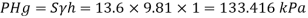
Consider pressure from A up to air
Let 'h' be the height of water
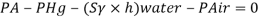
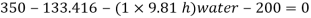
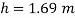
Height of water is 1.69 m
Now consider pressure from air up to gauge B Let P be the gauge pressure at B

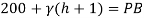
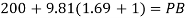
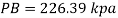
Pressure at B is 226.39 kPa (abs)
Q26) A 6 m deep tank contains 4 m of water and 2 m of oil of relative density 0.8. Determine the pressure at the bottom of the tank.
A26)

Specific weight
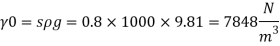
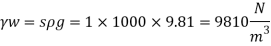
Q27) A closed tank of height 9.0 m is filled with bromine of specific gravity 3.1 to a depth of 2 m and turpentine of specific gravity 0.87 to a depth of 6m. The upper part of the tank contains air under a pressure of 25 kPa (vacuum). Find the absolute pressure at the bottom of the tank in kPa and in cm of mercury Neglect density of air. Consider atmospheric pressure 101.3 kPa.
A27)
Given:
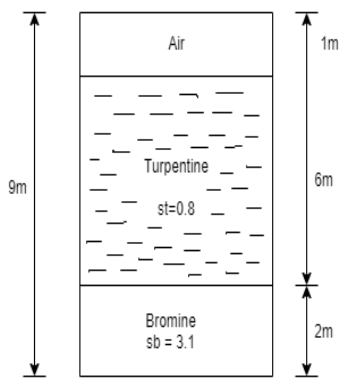
Atmospheric pressure
Patm= 101.3 kpa
Air pressure P=25 kPa (vacuum)
Gauge pressure at bottom of tank
= Air pressure + pressure due to turpentine + pressure due to bromine


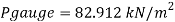
Absolute pressure

Pressure head in term mercury

Q28) The tank shown in Fig. P. Is closed at to and contains air at a pressure of P, Calculate the value of P, for the manometer reading as shown in Fig.
A28)
Given:
h₁ = 10 cm = 0.1 m,
h₂ = 150 cm= 15m
h3 = 200+10-150=60 cm=0.6 m

Consider section X-X, balance the fluid about X-X.
Pressure on left limb about XX= Pressure on right limb about X-X
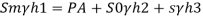
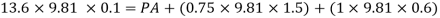
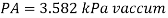
Q29) A vertical rectangular plane surface has width of 1.5 m and depth of 3.0 m. It is placed in water such that the upper edge is 1 m below free water surface. Find the total pressure and the depth of centre of pressure on the rectangular plane.
A29)
Given:
b= 1.5 m,
d = 3.0 m 1m,
s = 1 (water)
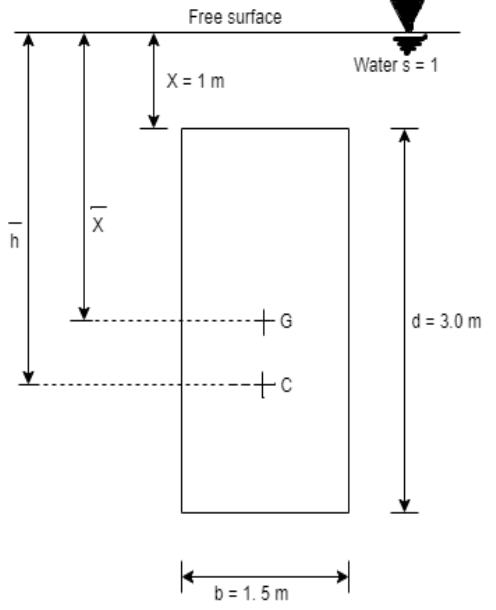
To find: P and h
Area A = b x d=1.5x3=4.5 m²
Distance of centroid of lamina from free surface,
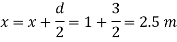
Total of inertia
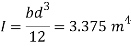
Total pressure,
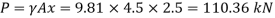
Centre of pressure,

Q30) A rectangular gate 2 m long and 1.5 m wide lies in a vertical plane with its centre 2.5 m below water surface. Calculate magnitude, direction and location of the total force on the gate.
A30)
Given:
x=2.5m, b = 2m, d=1.5m

To find
P and h
Moment of inertia
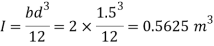
Total pressure

Centre of pressure
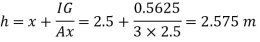
Q31) An isosceles triangular plate of base band altitude 'h' meter is immersed vertically in water with its apex below the base. The base is parallel to and vertical depth of 'd below free surface. Prove that the depth of pressure is equal to (h²-4dh+6d²)/ (3d+h)
A31)
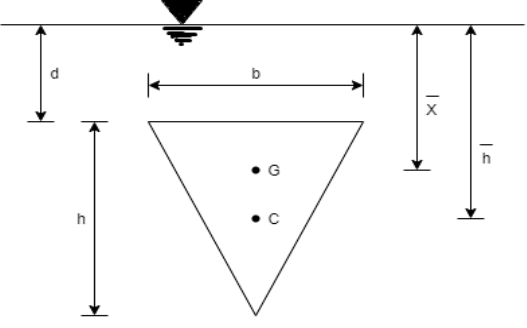
Distance of centroid from free surface
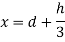
Area of triangle,

Moment of inertia
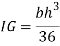
Centre of pressure
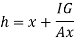
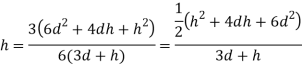
Q32) A circular plate 2.95 m diameter is immersed in water in such a way that its greatest and least depth below the free surface is 4.1 m and 1.6 m respectively. Determine the total pressure on one face of the plate and position of center of pressure.
A32)
Given:
d=2.95 m,
Least depth 1.6 m,
Greatest depth 4.1 m
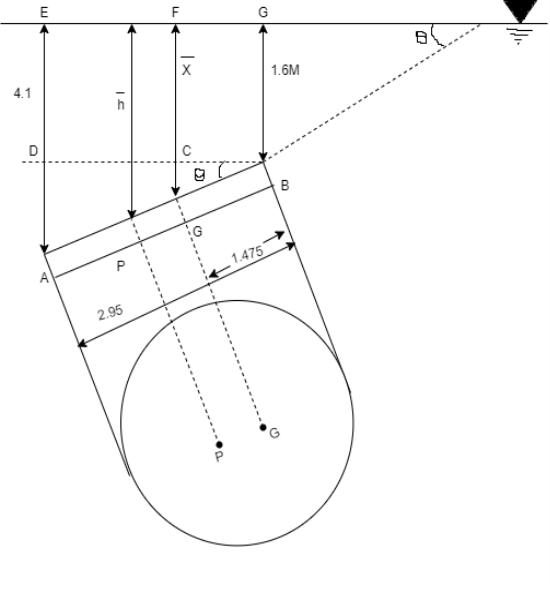
To Find: P and h
Area of plate
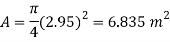
Moment of inertia
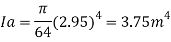
Distance of c. g. Of plate from free surface

1. Total pressure, p
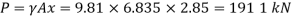
2. Position of center of pressure, h
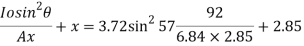
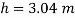
Q33) A square plate 6 m x 6 m is placed in a liquid of specific gravity 0.8 at an angle of 30 with free liquid surface. A square hole 1.5 m in size is cut exactly in the center of the plate. Its greatest and the least depths below the free liquid surface are 4 m and 2 m respectively. Determine the total pressure on one face of the plate and position of center of pressure.
A33)
Given: S=0.8, 0=30°
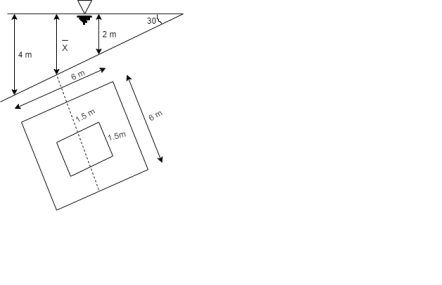
To Find: P and h
Area A=6²-1.5 = 33.75 m²
Position of centroid of lamina from free surface
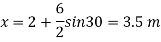
Moment of inertia,
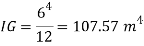
Total pressure,
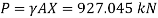
Q34) A solid cube of sides 0.5 m each is made of material of relative density 0.5. Tho cube floats in a liquid of relative density 0.95 with two of its faces horizontal. Examine its stability.
A34)
Given:

Side a=0.5 m
Relative density 0.5 m
Relative density of cube Sc= 0.5
Relative density of liquid S₁ = 0.95
Weight of cube = Weight of liquid displaced
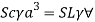
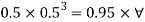

Depth of immersion (h).
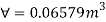
Depth of immersion (h),

Distance of C.G. From O.
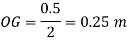
Distance of buoyancy from O.
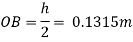
Now, BG= OG-OB=0.25-0.1315 = 0.1185 m

Metacentric height, BM-BG

Negative sign of metacentric height indicates that in unstable equilibrium.
Q35) A rectangular pontoon is 5 m long, 3 m wide and 1.20 m high. The depth of immersion of the pontoon is 0.80 m in sea water. If the centre of gravity is 0.6 m above the bottom of the pontoon, determine the metacentric height. The density for sea water = 1025 kg/m².
A35)

Volume of liquid displaced
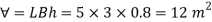
Moment of inertia
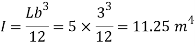
Metacentric height BM BG=

Unit - 2
Fluid Statics
Q1) Explain pressure at a point in fluid pressure?
A1)
- Have you ever seen a human tower? Consider the case of the man in the bottom line. You obviously carry a lot more weight than the guy in the first row. It is the same with the pressure of a liquid in a column. In the liquid column, as the depth increases, the pressure increases with it. And why is this pressure increasing? Because as it deepens, the liquid at lower depth should support the excess liquid as well. So to put it bluntly, we can say that
- Fluid pressure is the pressure within the fluid resulting from the weight of the liquid.
Liquid pressure can be calculated using the following relationships.

Fig no 1 Fluid measurement
P fluid = P + ρ g h
Where,
P = Pressure on the reference area
P fluid is the pressure at a point in a fluid
ρ is the density of the fluid
g acceleration due to gravity (considering earth g = 9.8 m / s)
h height from the reference point
The volume of this liquid can be calculated by dividing the volume of the liquid by considering the volume of the extracted liquid.
ρ = m / v
Where,
m the size of the liquid
v is the amount of liquid considered
When the liquid is under atmospheric pressure there is a total systemic pressure provided by
P fluid = Po + ρ g h
Where,
Po atmospheric pressure
Conditions for Consideration of fluid pressure:
Water pressure is considered in two cases:
- In open condition or open channel flow
- In a closed case or in a closed ditch
The pressure of the liquid given above is static fluid pressure or hydrostatic pressure. The pressure here is considered to be based on the depth of the liquid only because the pressure generated as a result of the flow of the liquid can be considered minimal. The intensity of static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
Remember that here, liquid refers to anything that has the ability to flow. Therefore, this refers to both beverages and gases.
Factors Affecting Fluid Pressure
There are two factors that affect liquid pressure. These two factors are the depth of the liquid and the quantity of it.
- Depth of fluid: As the depth increases, the pressure released by the fluid increases.
- Liquidity: A liquid as strong as water has a greater pressure than a liquid as light as air. The molecules in the denser fluid are close to each other leading to more collisions in a given area. This results in exertion and increased pressure.
Q2) Explain pascals law?
A2)
The pressure of the liquid given above is the constant pressure of water or hydrostatic pressure. The pressure here is considered to be based solely on the depth of the liquid because the pressure generated by the flow of the liquid can be considered minimal. The size of the static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
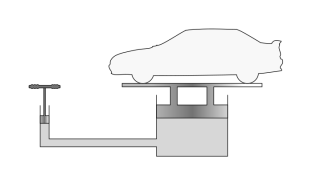
Fig no 2 Pascal's law is the principal behind hydraulic lifting and pressing device
Fig no 3 Pascal law applies for fluid
Pascal's law is defined as
- The change of pressure at any time in the closed liquid at rest is transmitted continuously to all points of the liquid.
- The pressure applied to the liquid in a sealed container is transmitted evenly and is not reduced to all parts of the container and applies with fairness to the closed walls.
- Another explanation: The pressure applied to any part of a closed fluid will be transmitted evenly across all directions of the liquid.
This principle is mathematically defined as:
∆p = ρ g ∆ h
Where
∆p hydrostatic pressure (given by pascals in the SI system), or the difference in pressure in two places within a liquid column, due to the weight of the liquid;
ρ the size of the water (per kilogram per cubic meter in the SI system);
g acceleration due to gravity (usually coastal acceleration due to gravity, meters per second);
∆h the height of the liquid above the measuring point, or the difference in height between two points within a column of water (in meters) .
- An accurate definition of this formula is that the change in pressure between the two heights is due to the weight of the liquid between the heights. Alternatively, the result can be interpreted as a pressure change caused by a potential energy change per unit of liquid due to the presence of a magnetic field. Pressures. Therefore, Pascal's law can be interpreted as any change in pressure applied to any point of fluid being transferred continuously throughout the liquid.
- The formula is a specific mathematical aspect of Navier - Stokes other than the words of inertia and viscosity.
- When the U-tube is filled with water and pistons are fitted at each end, the pressure carried by the left piston will be transferred to all the liquid and below the right piston. (Just four pistons "plugs" can slide freely but inside the tube.)
- The pressure on the left piston against the water will be exactly the same as the water pressure it does when facing the right piston. Suppose the tube on the right is widened and a large area piston is used; for example, the right piston has 50 times the position of the piston on the left.
- When a load of 1 N is placed on the left piston, additional pressure due to the weight of the load is transferred across the liquid and counteracts the larger piston.
- The difference between force and pressure is significant: additional pressure is found throughout the piston area. With an area 50 times larger, there is a 50 times greater force on a larger piston. Therefore, a larger piston will support 50 N load - 50 times the load on a smaller piston.
- Power can be doubled using such a device. One newton input shows the output of 50 newtons. By adding the location of a large piston (or reducing the area of a small piston), the forces can multiply, in fact, by any value. Pascal's foundation supports the operation of a compression machine.
- The hydraulic engine does not break energy savings, because the reduced distance traveled compensates for the increase in energy. When the small piston is removed to the ground by 100 inches, the larger piston will only be raised by fifty inches in this case, or by 2 inches.
- The input power multiplied by the distance transmitted by the small piston is equal to the output power multiplied by the distance transmitted by the large piston; this is just one example of a simple machine that works on the same principle as a machine lever.
- The most common use of Pascal's gas and fluid policy is a vehicle lift that is seen on most service stations (hydraulic jack). The increased air pressure generated by the air compressor is transferred through the air towards the surface of the oil in the underground pool.
- The oil, in turn, exerts pressure on the piston, which lifts the vehicle. The low pressure that exerts the piston lift is almost the same as the air pressure on the car's wheels. Hydraulics are used by modern machines ranging from the smallest to the largest.
- For example, there are pressure pistons on almost all construction equipment where heavy loads are touched.
Q3) Explain pressure variation with temperature and density altitude?
A3)
- When the gas is trapped inside a container with a fixed size (its volume cannot change) and the gas is heated, the particles will gain kinetic energy that will make it faster.
- Gas temperature is equal to the kinetic energy of its molecules. Fast moving particles will collide with container walls more often and with greater force. This causes the strength in the walls of the vessel to increase so the pressure increases.
- When the temperature of a gas is measured in Kelvin's scale, the pressure is equal to the temperature.
In this we can find equality
P1 /T1 = P2 /T2
Where:
P1 is the initial pressure
T1 is the initial temperature
P2 is the final pressure
T2 is the last heat
All temperatures were measured in Kelvin's temperature.
DENSITY ALTITUDE
- Maximum pressure is adjusted by constant temperature. As the temperature rises, the air pressure decreases. In a sense, the height at which a plane “feels” its flight.
- The height of the magnitude is the relative height of the atmospheric conditions where the magnitude of the air can be equal to the magnitude of the air indicated in the viewing area. In other words, the height of the density is the air pressure given as the height above means the sea. The maximum temperature can also be considered as the pressure height adjusted to the ambient temperature.
- Both an increase in temperature and a decrease in atmospheric pressure, and, to a lesser degree, an increase in humidity, will result in an increase in human density. In tropical and subtropical climates, the height of the mass in one area may be much higher than the true elevation.
- For aircraft, maximum altitude is used to test the performance of an airplane aircraft under certain weather conditions. The aviation impacts, as well as the relationship between its indicated airspeed (IAS) and its actual airspeed (TAS), are also subject to changes in wind power. In addition, the force exerted by an aircraft engine is affected by congestion and air conditioning.
Tips for flying at very high altitudes
- I will go in the evening or early morning when temperatures are low.
- Call a local instructor at your destination airport to discuss the flight arrangements at that airport.
- Before taking off for a high-end flight, be aware that your flight is taking off more efficiently with professional hits. Most planes do, but the results are varied and that the first note of the layers can add more drag than lift.
- Make sure the weight of the plane is less than 90 percent of the total weight.
- Do not fill tanks at the top (see previous tip).
- Fly short legs and make another fat stand (a suggestion that is hard to accept, but results in a less pleasant departure).
- Be prepared to take one passenger to the airport with the lowest possible traffic, then return to another. If you are unsure of the circumstances, fly around the pattern once alone without baggage to check the performance of your plane.
- Have an 80% speeding departure from the road area, or have an abortion. That means having 48 IAS knots in Cessna 172 in the middle.
Q4) Explain piezometer and u tube mano meter?
A4)
PIEZOMETER
- A piezometer is the simplest form of manometer which can be used for measuring moderate pressures of liquids.
- It consists of a glass tube inserted in the wall of a vessel or of a pipe, containing liquid whose pressure is to be measured.

Fig no 4 Piezometer tube fitted to open vessel

Fig no 5 Piezometer tube fitted to a closed pipe
- The tube extends vertically upward to such a height that liquid can freely rise in it without overflowing.
- The pressure at any point in the liquid is indicated by the height of the liquid in the tube above that point, which can be read on the scale attached to it.
- Thus if w is the specific weight of the liquid, then the pressure at point A(p) is given by p = wh
- A piezometer tube is not suitable or measuring negative pressure; as in such a case the air will enter in pipe through the tube.
U-TUBE MANOMETER
- Piezometer cannot be employed when large pressures in the lighter liquids are to be measured, since this would require very long tubes, which cannot be handled conveniently.
- Further more gas pressures cannot be measured by piezometer because a gas forms no free atmospheric surface.
- These limitations can be overcome by the use of U-tube manometers.
- A U-tube manometer consists of a glass tube but in U-shape, one end of which is connected to a point at which pressure is to be measured and other end remains open to the atmosphere as shown in fig.

(a). (b)
Fig no 6 Utube manometer
Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)
Let, h1 = height of the light liquid in the left limb above the datum line
h2 = height of the heavy liquid in the right limb above the datum line
h = pressure in pipe, expressed in terms of head
S1 = specific gravity of the light liquid, and
S2 = specific gravity of the heavy liquid
The pressure in the left limb and right limb above the datum line X-X are equal.
Pressure head above X-X line in the left limb = h+h1S1
Pressure head above X-X in the right limb = h2S2
Equating these two pressures, we get
For negative pressure:
Refer to fig(b)
Pressure head above x-x in the left limb=
Pressure head above x-x in the right limb = 0
Equating these two pressures, we get
h + h1S1 + h2S2 = 0 or h = - h2S2 - h1S1
Q5) Explain single column manometer?
A5)
This type of manometer is useful for the measurement of small pressures and is more sensitive than the vertical tube type.
Due to inclination the distance moved by the heavy liquid in the right limb is more.
l = length of the heavy liquid moved in right limb,
Alpha = inclination of right limb horizontal, and
h2 = vertical rise of liquid in right limb from x-x = l sin
h = l sin alpha × S2 - h1S1

Fig no 7 Single column manometer
Q6) Explain u tube differential manometer?
A6)
A U-tube differential manometer is shown in fig.
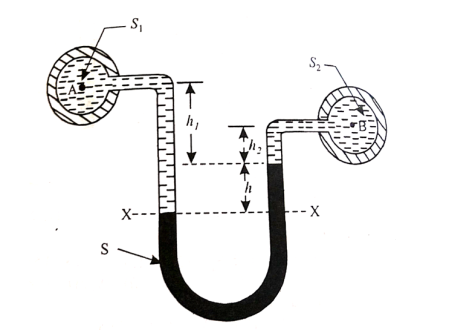
Fig no 8 Utube differential manometer
Let, h = difference of mercury level (heavy liquid) in the U-tube,
h1 = distance of the centre of A, from the mercury level in the left limb
h2 = distance of the centre of B, from the mercury level in the right limb,
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of heavy liquid o mercury
HA = pressure head at A,
HB = pressure head at B
Considering the pressure heads above the datum line x-x, we get
Pressure head in the left limb:
h A + ( h 1 + h ) S1
Pressure head in the right limb:
h B + h 2 × S 2 + h × S
Equating the above pressure heads, we get
h A + ( h1 + h ) S1 = h B + h 2 × S 2 + h× S
( h A - h B ) = h 2 × S 2 + h × S - ( h 1 + h ) S 1
Q7) Explain manometer?
A7)
- A micro manometer can be used - if required in combination with pitot tubes - to measure, measure, measure and calculate velocity and volumetric flow rate. Micro manometers have high accuracy for measuring high-, low- and variability. Observatory Instruments offer different micro manometers, each with a different application.
- One leg of the micro manometer is the source and the other is the inclined tube, which contains a magnifier. The meniscus in the inclined tube is located at a reliable level adjusted by the hairline viewed by the magnifier.
- First of all both the source and the amplifier are the same pressure. The application of pressure at the end of the spring removes the hairline but can be restored to its original position by increasing or lowering the source (mercury sump).
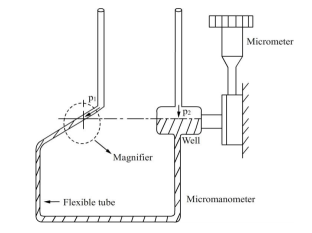
Fig no 9 Micro manometer
Q8) Explain pressure gauge?
A8)
Mechanical Gauges
- The manometers are suitable for comparatively low pressure.
- For high pressures, they become unnecessarily larger even when they are filled with heavy liquids.
- Therefore, for measuring medium and high pressures, we make use of elastic pressure gauges.
- They employ different forms of elastic systems such as tubes, diaphragms or bellows etc. to measure the pressure.
- The elastic deformation of these elements is used to show the effect of pressure. Since these elements are deformed within the elastic limit only, therefore these gauges are sometimes called elastic gauges.
Bourdon tube pressure gauge:
- Bourdon tube pressure gauge is used for measuring high as well as low pressure.
- In this case, the pressure element consists of a metal tube of approximately elliptical cross section.
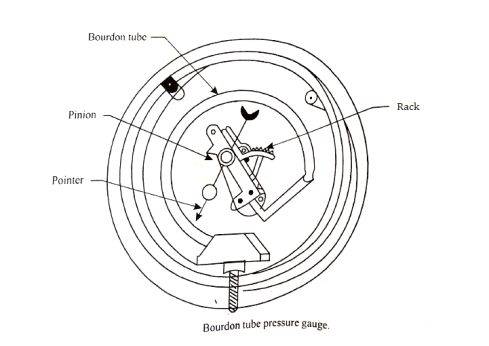
Fig no 10 Bourdon tube pressure gauge
- This tube is bent in the form of a segment of a circle and responds to pressure changes.
- When one end of the tube which is attached to the gauge case, is connected to the source of pressure, the internal pressure causes the tube to expand, whereby circumferential stress is set up.
- The free end of the tube moves and is in turn connected by suitable levers to a rack, which engages with a small pinion mounted on the same spindle as the pointer.
- Thus the pressure applied to the tube causes the rack and pinion to move.
- The pressure is indicated by the pointer over a dial which can be graduated in a suitable scale.
- The Bourdon tube are generally made of bronze or nickel steel.
- The former is generally used for low pressures and the latter for high pressures.
Diaphragm Gauge:
- This type of gauge employs a metallic disc or diaphragm instead of a bent tube.
- This disc or diaphragm is used for actuating the indicated device.

Fig no 11 Diaphragm gauge
- When pressure is applied on the lower side of the diaphragm it is deflected upward.
- This movement of the diaphragm is transmitted to a rack and pinion.
- The latter is attached to the spindle of needle moving on a graduated dial.
- The dial can again be graduated in a suitable scale.
Vacuum gauge:
- Bourdon gauges discussed earlier can be used to measure vacuum instead of pressure.
- Slight changes in the design are required in this purpose.
- Thus, in this case, the tube be bent inward instead of outward as in pressure gauges.
- Vacuum gauges are graduated in millimeters of mercury below atmospheric pressure.
- In such cases, therefore, absolute pressure in millimeters of mercury is the difference between barometer reading and vacuum gauge reading.
- Vacuum gauges are used to measure the vacuum in the condensers etc. If there is leakage, the vacuum will drop.
Q9) Explain hydrostatic pressure force like horizontal, vertical and inclined surface?
A9)
Fluid Statics
- Fluid Statics interacts with the relaxing fluid while Fluid Dynamics explores the flow fluid.
- Any improved power is caused only by normal pressure i.e., pressure. Such a condition is called hydrostatic condition.
- Fluid Statics is also known as Hydrostatics.
- The static fluid cannot have the shear strength to which it operates, and that any force between the liquid and the boundary must operate in a direct way across the boundary.
- As for the liquid at rest, the factor will be proportional. The total number of energy components in any direction will be zero. The sum of the times the power of an object at any point and should be zero.
- Inside the liquid, the pressure is the same at all points in all directions.
- The pressure on the wall of any ship is toward the wall
- The pressure due to the depth is P = ρgh, and is the same for any specific level of the connected liquid.
Fluid Pressure at a point
- If the liquid is dry, then the force acting on any area or area is unique to that area.
- If the force is present in each area of the same boundary, the pressure is said to be the same
Fig no 12 Hydrostatic force on surface
Pascal's Law of Pressure at a Point
- It states that the pressure or pressure somewhere in the static fluid (liquid rest) is equal in all directions. If the fluid does not move according to Pascal's law,
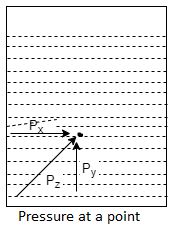
Fig no 13 Pressure at a point
Px = py = pz
Where, px, py and pz pressure point x, y, z respectively.
A typical equation of pressure variability in Static Fluid
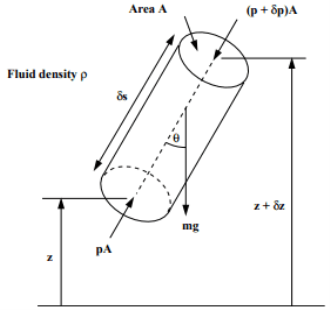
Fig no 14 Pressure variability in static fluid
Dp / d s = -  g cos
g cos 
Vertical Variation of pressure in a fluid under gravity
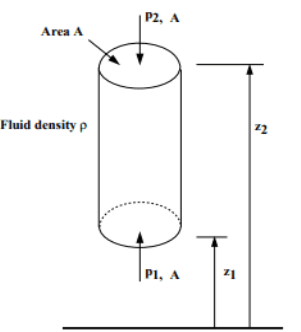
Fig no 15 Vertical Variation of pressure in a fluid
Taking upward as positive, we have
Vertical cylindrical structure of a liquid body = A
Metal size = ρ
The force involved are:
- Force for p1 to A (top) = p1. A
- Force for p2 to A (bottom) = p2. A
- Forcing due to the weight of the material (bottom) = mg
= mass density x volume x g
= ρ.gA.A. (z2 - z1)
Thus in a liquid that is below gravity, the pressure decreases proportionally with the elevation
p2 - p1 = ρgA (z2 - z1)
This is a change in hydrostatic pressure.
Equilibrium of Pressure at Equivalent Static Fluid

Fig no 16 Pressure act on horizontal surface
Horizontal element of cylindrical cross sectional area = A
Metal size = ρ
Left end pressure = pl
Right end pressure = pr
Equally, the total energy in direction x is zero = pl. A = pr. A
Pl = pr
Therefore, the pressure in the horizontal direction does not change.

Fig no 17 Pressure in horizontal direction
As we know, P1 = pr

Therefore, the pressure at two equal levels is the same.
Total Hydrostatic Force in the Facial Area
- On the surface of a liquid plane submerged in a liquid, or in the airplane inside a gas chamber, or in another part of the aircraft under the same hydrostatic pressure, the total hydrostatic power is given by
F = p. A
Where p is the same pressure and A is the area.
- Generally, the total hydrostatic pressure in any aircraft area is equal to the local product output and the unit pressure at its center of gravity.
F = pcg. A
When the pcg pressure is in the center of gravity.
- To get the same free liquid at rest, the number can be displayed according to the unit weight γ of the liquid.
F = γh'A
Where h 'is the depth of the liquid above the centroid of the immersed area.
Q10) Explain buoyancy stability of floating bodies?
A10)
- Whenever a body is immersed wholly or partially in a fluid it is subjected to an upward force which tends to lift it up.
- The tendency for an immersed body to be lifted up in the fluid due to an upward force opposite to action of gravity is known as buoyancy.
- The force tending to lift up the body under such conditions is known as buoyant force or force of buoyancy.
- The magnitude of the buoyant force can be determined by Archimedes principle which states as follows:
- When a body is immersed in a fluid either wholly or partially it is buoyed or lifted up by a force which is equal to the weight of fluid displaced by the body.
Centre of Buoyancy
- The point of application of the force of buoyancy on the body is known as the center of buoyancy. It is always the center of gravity of the volume of fluid displaced.
Equilibrium of floating and submerged bodies
Stability of floating Body:
The stability of a floating body is determined from the position of Meta-centre (M).
a). Stable Equilibrium
- If the point M is above G, the floating body will be in stable equilibrium as shown in Fig.
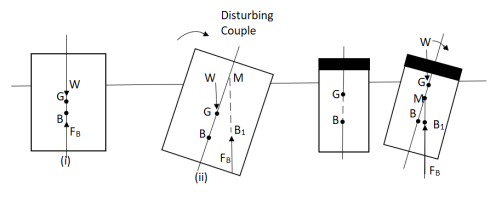
M is above G ( stable equilibrium ). M is below G ( unstable equilibrium )
Fig no 18 Stability of floating bodies
- If a slight angular displacement is given to the floating body in the clockwise direction, the center of buoyancy shifts from B to B1, such that the vertical line through B1 cuts at M.
- Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anti-clockwise direction and thus bringing the floating body in the original position.
b. Unstable Equilibrium:
- If the point M is below G, the floating body will be in unstable equilibrium as shown in fig.
- The disturbing couple is acting in the clockwise direction.
- The couple due to buoyant force FB and W is also acting in clock direction and thus overturning the floating body.
c. Neutral Equilibrium:
- If the point M is at the center of gravity of the body. The floating body will be in neutral equilibrium.
Stability of submerged Body:
- The position of center of gravity ¢er of buoyancy in case of a completely submerged body are fixed.
- Weight W acting vertically downward through G, while the buoyant force FB is acting vertical up through B.
Stable equilibrium :
When W = FB& point B is above G, the body is said to be in stable equilibrium.
Unstable Equilibrium :
If W = FB , but center of buoyancy B is below the center of gravity G, the body is in unstable equilibrium.
Neutral Equilibrium :
If W = FB & point B & G are at the same point, the body is said to be in neutral equilibrium.
Q11) Barometric reading at a place is 75 cm of Hg. Express the pressure intensity of 10 N per cm² is:
(1) m of water
(2) mm of mercury
(3) KN.m^2 abs
A11)
Given:
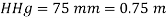
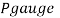 = 10 N/cm² = 100 kN/m².
= 10 N/cm² = 100 kN/m².
(i) In m of water,

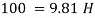

(ii) In mm of mercury

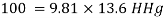
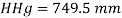
(iii) In kN/m absolute,
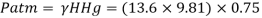
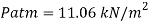
Absolute pressure,

Q12) A gauge on suction side of pump shows a negative pressure of 0.285 bar. Express this pressure in terms of
1. Pressure intensity kPa
2. N/m absolute
3. m of water gauge
4. m of oil (S0.85) absolute
5. Cm of mercury gauge.
Take atmospheric pressure as 76cm of mercury and relative density of mercury as 13.6.
A12)
1 bar = 10'^5 Pa
Gauge vacuum reading
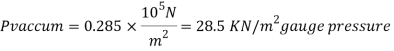
Absolute pressure
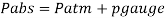
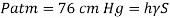
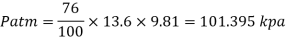
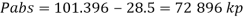
Equivalent head of water (gauge)

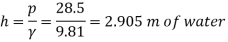
Equivalent head of oil (absolute)
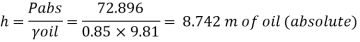
Head of mercury (gauge)


Q13) A cylinder contains a fluid at a gauge pressure of 350kPa. Express the pressure in terms of the column height of (a) water (o 1000kg/m) (b) Hg (S= 13.6). What would be absolute pressure in the cylinder if the atmospheric pressure is 101.3kPa?
A13)
Given:

(a) Pressure in term column head of water,
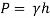

(b) Pressure head in terms of Hg

(c) Absolute Pressure

Q14) Mass density of a liquid varies as p = (1000+ 0.008 h). Where 'h' is depth (m) below free surface of liquid. Determine depth at which gauge pressure would be 100 kPa.
A14)
Given: 
To find: Depth?
Pressure at any point
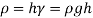


Q15) Measurements of pressure at the base and top of a mountain are 74cm and 60cm of mercury respectively. Workout the height of mountain if air has specific weight 11.97 N/m²
A15)
Pressure at top
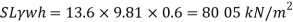
Pressure at bottom
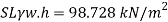
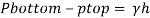
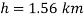
Q16) A piezo meter tube is fitted to a tank containing water at a point 600 mm above the tank. The liquid in the manometer is carbon bi Sulphide having a specific gravity of 1.9. Find the height of the free water surface above the bottom of the tank if the piezo meter reading 700 mm. Find also the pressure intensity at the bottom of the tank. Dec. 2005, 4 Marks
A16)
Pressure at end of piezometer
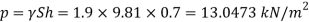
Height of water above point A

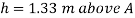
Height of free surface above bottom of tank
H = h +0.6
= 1.33 +0.6 = 1.93m
Pressure at bottom of tank

Q17) A piezometer tube is fitted to a tank containing water at a point 500 mm above the bottom of the tank. The liquid in the manometer is carbon tetrachloride (sp. Gr. 1.6). Find the height of the free water surface above the bottom of the tank if the piezometer reading is 600 mm. Find the pressure intensity at the bottom of the tank.
A17)
For static equilibrium

Pressure in the tank at point A= pressure due to piezometric liquid at A
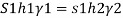

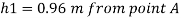
Total height of the free water surface above bottom of tank
h =h₁+0.5 = 0.96 + 0.5 = 1.46 m
Pressure intensity at the bottom of the tank

Q18) A simple U-tube manometer is used to measure water pressure in pipe line. The left limb of manometer connected to the pipe and the night limb is open to atmosphere. The mercury level in the left limb is 80mm below the center of the pipe and the level in the right limb in 220mm above the center of the pipe. Calculate the pressure of water in meter and also in km
A18)
Oil
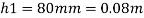
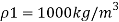
Mercury

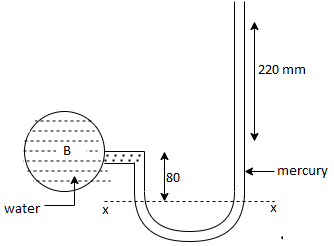

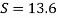
Pressure in the left limb about xx = Pressure in the right limb about x-s
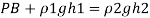
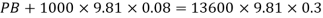
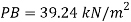
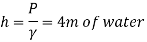
Q19) A U-tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The night limb of the manometer contains mercury and is open to atmosphere. The contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tule 12 cm and the free surface of mercury is in level with the centre of the pipe. It the pressure of water in pipe he is reduced to 9810 N/m². Calculate the new difference in the level of mercury.
A19)
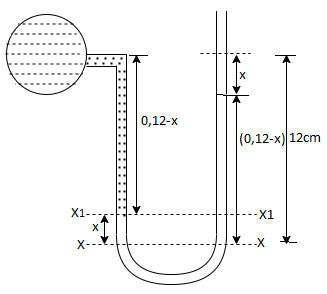
Case I
Given:
h1,=h₂= 12cm=0.12 m.
S2=13.6
Pressure in pipe
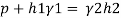


Case II
Since the pressure in the pipe is reduced to 9.81 kN/m² (which is less than 14.83 kN/m²), the mercury in the left limp will be rise. Rise of mercury in the left limb will be equal to the fall of mercury in right limb as the total volume of mercury remains same.
Let x = rise of mercury in left limb= fall in mercury in right limb,
Pressure at new section x₁ - x₁

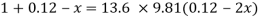

.. New difference of mercury

Q20) Fig. P shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer given in the Fig. P. 3.7.15 shows when the vessel is empty. Find the reading of the manometer when the vessel is completely filled with water.
A20)

Case I:
Vessel is empty
Pressure in left limb about x-x= Pressure in right limb about x-x
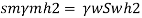
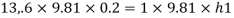
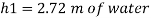
Case II: Vessel is full of water
When pressure is full of water, the pressure in right limb will increase and mercury level will fall by 'y' m, similarly Hg level in left limb will rise by 'y' m
Now consider 7-7 as a datum
Pressure in left limb = Pressure in right limb about z-z

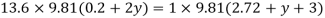

:. Difference of mercury level when the vessel is full of
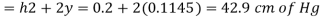
Q21) A differential manometer is connected at two points A and B of two pipes as shown in Fig. Pipe A contains liquid of specific gravity 1.6, while pipe B contains liquid of specific gravity 0.8. If the pressure at A and B are 11.80 x 10 N/m² and 19.60 x 10 N/m2, find the difference in mercury level in the differential manometer.
A21)
Pipe A
S₁ = 1.6
PA = 11.8 x 10' N/m² = 118 kN/m² 19.62× 10¹ N/m² = 196.2 kN/m²
h₁ = (2+1,5) = 3.5 h₂ = (1.5 + h)
Pipe B
s2= 0.8
h2= 1.5+h

Pressure in left limb = pressure in right limb PA

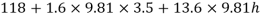
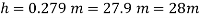
Q22) A U-tube manometer (Fig. P.) measures the pressure difference between two points A and B in a liquid of density PL The U tube contains mercury of density pa. Calculate the difference of pressure between points A and B in a liquid of density p, The u tube contains mercury of density P Calculate the difference of pressure between points A and B if the liquid contain at A is water take a 1.5 m, b=0.75 m and h= 0.50 m.
A22)
Given:
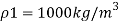



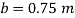
To find :
PA-PB
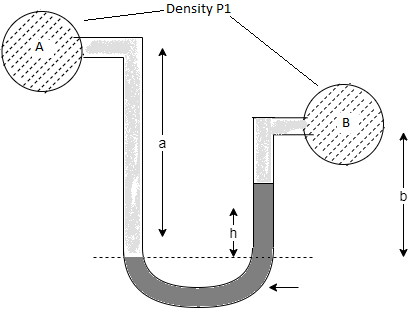
Pressure in left limb = Pressure in right limb
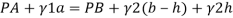
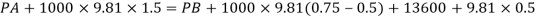

Q23) Liquid of specific gravity 1.0 flows through pipes A and B at positive pressures of 0.5 bar and 0.25 bar respectively. Pipe A is 1.8 m higher than B. What would be the difference in the levels of U-tube manometer connected to A and B, having manometric liquid of specific gravity 13.6 ? Liquid level in the limb attached to A is lower than that in the order.
A23)
Given:
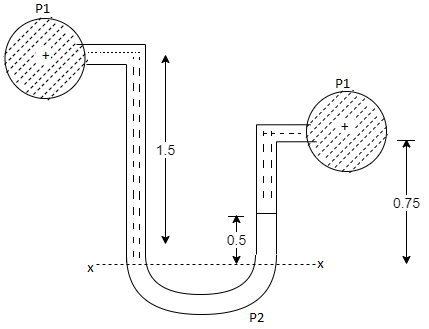
1 1bar = 10^5 N/m²,
2 P=0.5 bar = 50 kN/m².
3 pB= 0.25 bar 25 kN/m²
Balancing the liquid about x-x in left limb and right limb
Pressure in left limb about x-x= Pressure in right limb about x-x
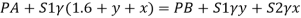
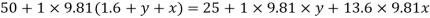
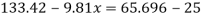

Q24) A pressure gauge, calibrated to read volume of fuel, is used as a fuel gauge. It is connected at the bottom of a fuel tank of area 267 cm². The gauge is calibrated to read maximum volume of 8 liters. If there accumulates 1 cm layer of water in the tank, how much fuel is measured when the gauge shows full scale reading? Assume density of fuel 730 kg/m².
A24)
Given:
Tank base Area A = 267 cm² = 267 x 10 m²
Max. Volume V = 8 liters = 8 x 10¹ m²
Density of fuel p₁ = 730 kg/m
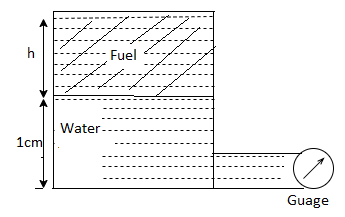
Depth of fuel for maximum volume
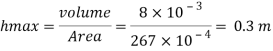
Max. Pressure for which gauge is calibrated
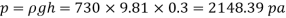
Total pressure due to water + Pressure due to fuel
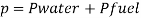
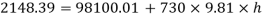

Volume of fuel

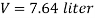
For full scale reading, volume of fuel is 7.64 liter
Q25) Gauge A attached at the bottom of a tank shown in Fig. P. 3.7.7 reads 350 kPa (absolute). What is the height 'h' of water? What is the reading of gauge B?
A25)
Given:
P = 350 (absolute)
Pressure due to mercury
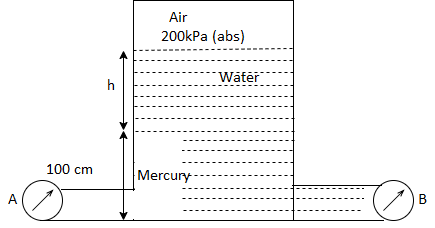

Consider pressure from A up to air
Let 'h' be the height of water

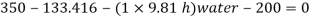
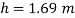
Height of water is 1.69 m
Now consider pressure from air up to gauge B Let P be the gauge pressure at B




Pressure at B is 226.39 kPa (abs)
Q26) A 6 m deep tank contains 4 m of water and 2 m of oil of relative density 0.8. Determine the pressure at the bottom of the tank.
A26)
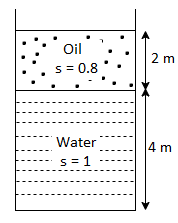
Specific weight


Q27) A closed tank of height 9.0 m is filled with bromine of specific gravity 3.1 to a depth of 2 m and turpentine of specific gravity 0.87 to a depth of 6m. The upper part of the tank contains air under a pressure of 25 kPa (vacuum). Find the absolute pressure at the bottom of the tank in kPa and in cm of mercury Neglect density of air. Consider atmospheric pressure 101.3 kPa.
A27)
Given:
Atmospheric pressure
Patm= 101.3 kpa
Air pressure P=25 kPa (vacuum)
Gauge pressure at bottom of tank
= Air pressure + pressure due to turpentine + pressure due to bromine
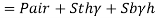
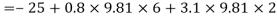

Absolute pressure
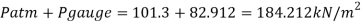
Pressure head in term mercury
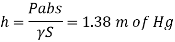
Q28) The tank shown in Fig. P. Is closed at to and contains air at a pressure of P, Calculate the value of P, for the manometer reading as shown in Fig.
A28)
Given:
h₁ = 10 cm = 0.1 m,
h₂ = 150 cm= 15m
h3 = 200+10-150=60 cm=0.6 m
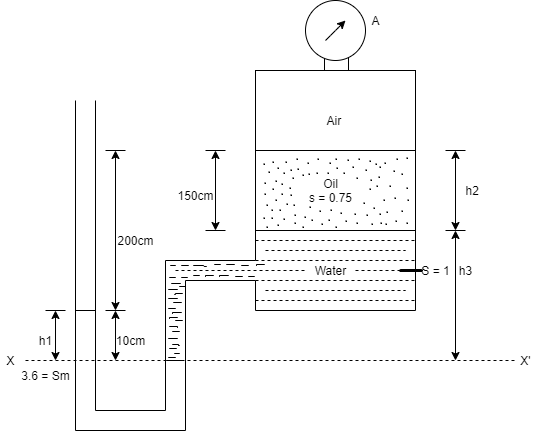
Consider section X-X, balance the fluid about X-X.
Pressure on left limb about XX= Pressure on right limb about X-X
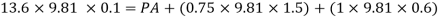

Q29) A vertical rectangular plane surface has width of 1.5 m and depth of 3.0 m. It is placed in water such that the upper edge is 1 m below free water surface. Find the total pressure and the depth of centre of pressure on the rectangular plane.
A29)
Given:
b= 1.5 m,
d = 3.0 m 1m,
s = 1 (water)
To find: P and h
Area A = b x d=1.5x3=4.5 m²
Distance of centroid of lamina from free surface,
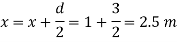
Total of inertia
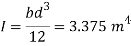
Total pressure,

Centre of pressure,
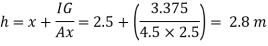
Q30) A rectangular gate 2 m long and 1.5 m wide lies in a vertical plane with its centre 2.5 m below water surface. Calculate magnitude, direction and location of the total force on the gate.
A30)
Given:
x=2.5m, b = 2m, d=1.5m
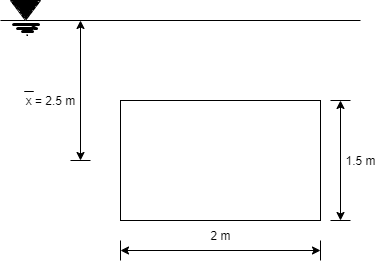
To find
P and h
Moment of inertia
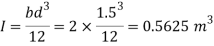
Total pressure
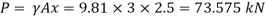
Centre of pressure
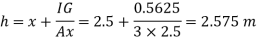
Q31) An isosceles triangular plate of base band altitude 'h' meter is immersed vertically in water with its apex below the base. The base is parallel to and vertical depth of 'd below free surface. Prove that the depth of pressure is equal to (h²-4dh+6d²)/ (3d+h)
A31)

Distance of centroid from free surface

Area of triangle,

Moment of inertia
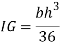
Centre of pressure
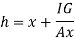
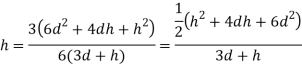
Q32) A circular plate 2.95 m diameter is immersed in water in such a way that its greatest and least depth below the free surface is 4.1 m and 1.6 m respectively. Determine the total pressure on one face of the plate and position of center of pressure.
A32)
Given:
d=2.95 m,
Least depth 1.6 m,
Greatest depth 4.1 m
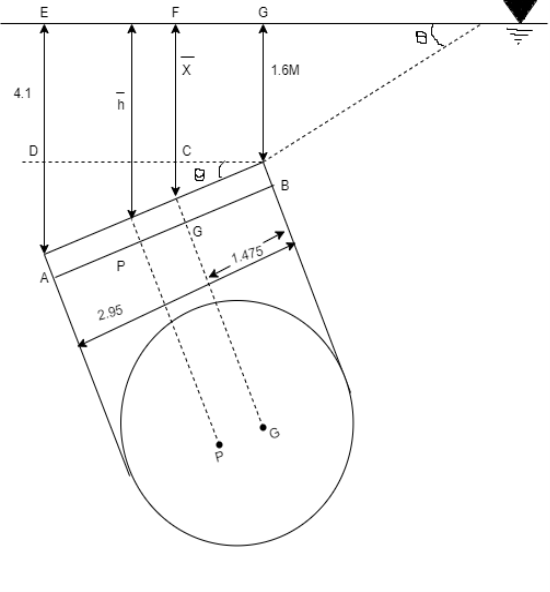
To Find: P and h
Area of plate

Moment of inertia

Distance of c. g. Of plate from free surface
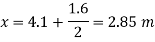
1. Total pressure, p

2. Position of center of pressure, h

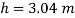
Q33) A square plate 6 m x 6 m is placed in a liquid of specific gravity 0.8 at an angle of 30 with free liquid surface. A square hole 1.5 m in size is cut exactly in the center of the plate. Its greatest and the least depths below the free liquid surface are 4 m and 2 m respectively. Determine the total pressure on one face of the plate and position of center of pressure.
A33)
Given: S=0.8, 0=30°
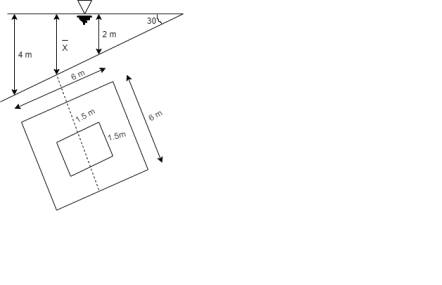
To Find: P and h
Area A=6²-1.5 = 33.75 m²
Position of centroid of lamina from free surface

Moment of inertia,
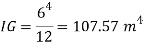
Total pressure,
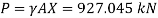
Q34) A solid cube of sides 0.5 m each is made of material of relative density 0.5. Tho cube floats in a liquid of relative density 0.95 with two of its faces horizontal. Examine its stability.
A34)
Given:
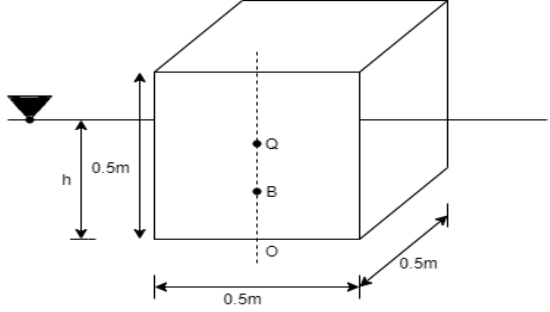
Side a=0.5 m
Relative density 0.5 m
Relative density of cube Sc= 0.5
Relative density of liquid S₁ = 0.95
Weight of cube = Weight of liquid displaced
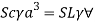
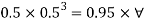
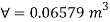
Depth of immersion (h).
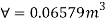
Depth of immersion (h),
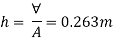
Distance of C.G. From O.
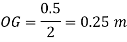
Distance of buoyancy from O.
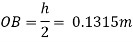
Now, BG= OG-OB=0.25-0.1315 = 0.1185 m
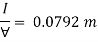
Metacentric height, BM-BG
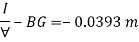
Negative sign of metacentric height indicates that in unstable equilibrium.
Q35) A rectangular pontoon is 5 m long, 3 m wide and 1.20 m high. The depth of immersion of the pontoon is 0.80 m in sea water. If the centre of gravity is 0.6 m above the bottom of the pontoon, determine the metacentric height. The density for sea water = 1025 kg/m².
A35)

Volume of liquid displaced
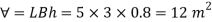
Moment of inertia

Metacentric height BM BG=

Unit - 2
Unit - 2
Unit - 2
Fluid Statics
Q1) Explain pressure at a point in fluid pressure?
A1)
- Have you ever seen a human tower? Consider the case of the man in the bottom line. You obviously carry a lot more weight than the guy in the first row. It is the same with the pressure of a liquid in a column. In the liquid column, as the depth increases, the pressure increases with it. And why is this pressure increasing? Because as it deepens, the liquid at lower depth should support the excess liquid as well. So to put it bluntly, we can say that
- Fluid pressure is the pressure within the fluid resulting from the weight of the liquid.
Liquid pressure can be calculated using the following relationships.
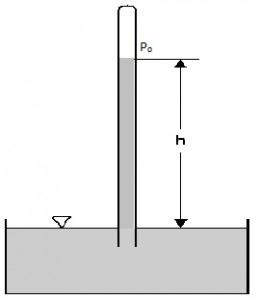
Fig no 1 Fluid measurement
P fluid = P + ρ g h
Where,
P = Pressure on the reference area
P fluid is the pressure at a point in a fluid
ρ is the density of the fluid
g acceleration due to gravity (considering earth g = 9.8 m / s)
h height from the reference point
The volume of this liquid can be calculated by dividing the volume of the liquid by considering the volume of the extracted liquid.
ρ = m / v
Where,
m the size of the liquid
v is the amount of liquid considered
When the liquid is under atmospheric pressure there is a total systemic pressure provided by
P fluid = Po + ρ g h
Where,
Po atmospheric pressure
Conditions for Consideration of fluid pressure:
Water pressure is considered in two cases:
- In open condition or open channel flow
- In a closed case or in a closed ditch
The pressure of the liquid given above is static fluid pressure or hydrostatic pressure. The pressure here is considered to be based on the depth of the liquid only because the pressure generated as a result of the flow of the liquid can be considered minimal. The intensity of static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
Remember that here, liquid refers to anything that has the ability to flow. Therefore, this refers to both beverages and gases.
Factors Affecting Fluid Pressure
There are two factors that affect liquid pressure. These two factors are the depth of the liquid and the quantity of it.
- Depth of fluid: As the depth increases, the pressure released by the fluid increases.
- Liquidity: A liquid as strong as water has a greater pressure than a liquid as light as air. The molecules in the denser fluid are close to each other leading to more collisions in a given area. This results in exertion and increased pressure.
Q2) Explain pascals law?
A2)
The pressure of the liquid given above is the constant pressure of water or hydrostatic pressure. The pressure here is considered to be based solely on the depth of the liquid because the pressure generated by the flow of the liquid can be considered minimal. The size of the static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.

Fig no 2 Pascal's law is the principal behind hydraulic lifting and pressing device
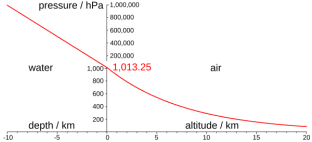
Fig no 3 Pascal law applies for fluid
Pascal's law is defined as
- The change of pressure at any time in the closed liquid at rest is transmitted continuously to all points of the liquid.
- The pressure applied to the liquid in a sealed container is transmitted evenly and is not reduced to all parts of the container and applies with fairness to the closed walls.
- Another explanation: The pressure applied to any part of a closed fluid will be transmitted evenly across all directions of the liquid.
This principle is mathematically defined as:
∆p = ρ g ∆ h
Where
∆p hydrostatic pressure (given by pascals in the SI system), or the difference in pressure in two places within a liquid column, due to the weight of the liquid;
ρ the size of the water (per kilogram per cubic meter in the SI system);
g acceleration due to gravity (usually coastal acceleration due to gravity, meters per second);
∆h the height of the liquid above the measuring point, or the difference in height between two points within a column of water (in meters) .
- An accurate definition of this formula is that the change in pressure between the two heights is due to the weight of the liquid between the heights. Alternatively, the result can be interpreted as a pressure change caused by a potential energy change per unit of liquid due to the presence of a magnetic field. Pressures. Therefore, Pascal's law can be interpreted as any change in pressure applied to any point of fluid being transferred continuously throughout the liquid.
- The formula is a specific mathematical aspect of Navier - Stokes other than the words of inertia and viscosity.
- When the U-tube is filled with water and pistons are fitted at each end, the pressure carried by the left piston will be transferred to all the liquid and below the right piston. (Just four pistons "plugs" can slide freely but inside the tube.)
- The pressure on the left piston against the water will be exactly the same as the water pressure it does when facing the right piston. Suppose the tube on the right is widened and a large area piston is used; for example, the right piston has 50 times the position of the piston on the left.
- When a load of 1 N is placed on the left piston, additional pressure due to the weight of the load is transferred across the liquid and counteracts the larger piston.
- The difference between force and pressure is significant: additional pressure is found throughout the piston area. With an area 50 times larger, there is a 50 times greater force on a larger piston. Therefore, a larger piston will support 50 N load - 50 times the load on a smaller piston.
- Power can be doubled using such a device. One newton input shows the output of 50 newtons. By adding the location of a large piston (or reducing the area of a small piston), the forces can multiply, in fact, by any value. Pascal's foundation supports the operation of a compression machine.
- The hydraulic engine does not break energy savings, because the reduced distance traveled compensates for the increase in energy. When the small piston is removed to the ground by 100 inches, the larger piston will only be raised by fifty inches in this case, or by 2 inches.
- The input power multiplied by the distance transmitted by the small piston is equal to the output power multiplied by the distance transmitted by the large piston; this is just one example of a simple machine that works on the same principle as a machine lever.
- The most common use of Pascal's gas and fluid policy is a vehicle lift that is seen on most service stations (hydraulic jack). The increased air pressure generated by the air compressor is transferred through the air towards the surface of the oil in the underground pool.
- The oil, in turn, exerts pressure on the piston, which lifts the vehicle. The low pressure that exerts the piston lift is almost the same as the air pressure on the car's wheels. Hydraulics are used by modern machines ranging from the smallest to the largest.
- For example, there are pressure pistons on almost all construction equipment where heavy loads are touched.
Q3) Explain pressure variation with temperature and density altitude?
A3)
- When the gas is trapped inside a container with a fixed size (its volume cannot change) and the gas is heated, the particles will gain kinetic energy that will make it faster.
- Gas temperature is equal to the kinetic energy of its molecules. Fast moving particles will collide with container walls more often and with greater force. This causes the strength in the walls of the vessel to increase so the pressure increases.
- When the temperature of a gas is measured in Kelvin's scale, the pressure is equal to the temperature.
In this we can find equality
P1 /T1 = P2 /T2
Where:
P1 is the initial pressure
T1 is the initial temperature
P2 is the final pressure
T2 is the last heat
All temperatures were measured in Kelvin's temperature.
DENSITY ALTITUDE
- Maximum pressure is adjusted by constant temperature. As the temperature rises, the air pressure decreases. In a sense, the height at which a plane “feels” its flight.
- The height of the magnitude is the relative height of the atmospheric conditions where the magnitude of the air can be equal to the magnitude of the air indicated in the viewing area. In other words, the height of the density is the air pressure given as the height above means the sea. The maximum temperature can also be considered as the pressure height adjusted to the ambient temperature.
- Both an increase in temperature and a decrease in atmospheric pressure, and, to a lesser degree, an increase in humidity, will result in an increase in human density. In tropical and subtropical climates, the height of the mass in one area may be much higher than the true elevation.
- For aircraft, maximum altitude is used to test the performance of an airplane aircraft under certain weather conditions. The aviation impacts, as well as the relationship between its indicated airspeed (IAS) and its actual airspeed (TAS), are also subject to changes in wind power. In addition, the force exerted by an aircraft engine is affected by congestion and air conditioning.
Tips for flying at very high altitudes
- I will go in the evening or early morning when temperatures are low.
- Call a local instructor at your destination airport to discuss the flight arrangements at that airport.
- Before taking off for a high-end flight, be aware that your flight is taking off more efficiently with professional hits. Most planes do, but the results are varied and that the first note of the layers can add more drag than lift.
- Make sure the weight of the plane is less than 90 percent of the total weight.
- Do not fill tanks at the top (see previous tip).
- Fly short legs and make another fat stand (a suggestion that is hard to accept, but results in a less pleasant departure).
- Be prepared to take one passenger to the airport with the lowest possible traffic, then return to another. If you are unsure of the circumstances, fly around the pattern once alone without baggage to check the performance of your plane.
- Have an 80% speeding departure from the road area, or have an abortion. That means having 48 IAS knots in Cessna 172 in the middle.
Q4) Explain piezometer and u tube mano meter?
A4)
PIEZOMETER
- A piezometer is the simplest form of manometer which can be used for measuring moderate pressures of liquids.
- It consists of a glass tube inserted in the wall of a vessel or of a pipe, containing liquid whose pressure is to be measured.
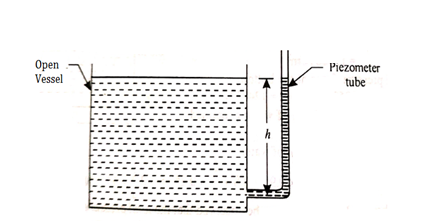
Fig no 4 Piezometer tube fitted to open vessel
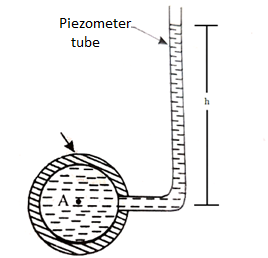
Fig no 5 Piezometer tube fitted to a closed pipe
- The tube extends vertically upward to such a height that liquid can freely rise in it without overflowing.
- The pressure at any point in the liquid is indicated by the height of the liquid in the tube above that point, which can be read on the scale attached to it.
- Thus if w is the specific weight of the liquid, then the pressure at point A(p) is given by p = wh
- A piezometer tube is not suitable or measuring negative pressure; as in such a case the air will enter in pipe through the tube.
U-TUBE MANOMETER
- Piezometer cannot be employed when large pressures in the lighter liquids are to be measured, since this would require very long tubes, which cannot be handled conveniently.
- Further more gas pressures cannot be measured by piezometer because a gas forms no free atmospheric surface.
- These limitations can be overcome by the use of U-tube manometers.
- A U-tube manometer consists of a glass tube but in U-shape, one end of which is connected to a point at which pressure is to be measured and other end remains open to the atmosphere as shown in fig.

(a). (b)
Fig no 6 Utube manometer
Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)
Let, h1 = height of the light liquid in the left limb above the datum line
h2 = height of the heavy liquid in the right limb above the datum line
h = pressure in pipe, expressed in terms of head
S1 = specific gravity of the light liquid, and
S2 = specific gravity of the heavy liquid
The pressure in the left limb and right limb above the datum line X-X are equal.
Pressure head above X-X line in the left limb = h+h1S1
Pressure head above X-X in the right limb = h2S2
Equating these two pressures, we get
For negative pressure:
Refer to fig(b)
Pressure head above x-x in the left limb=
Pressure head above x-x in the right limb = 0
Equating these two pressures, we get
h + h1S1 + h2S2 = 0 or h = - h2S2 - h1S1
Q5) Explain single column manometer?
A5)
This type of manometer is useful for the measurement of small pressures and is more sensitive than the vertical tube type.
Due to inclination the distance moved by the heavy liquid in the right limb is more.
l = length of the heavy liquid moved in right limb,
Alpha = inclination of right limb horizontal, and
h2 = vertical rise of liquid in right limb from x-x = l sin
h = l sin alpha × S2 - h1S1

Fig no 7 Single column manometer
Q6) Explain u tube differential manometer?
A6)
A U-tube differential manometer is shown in fig.
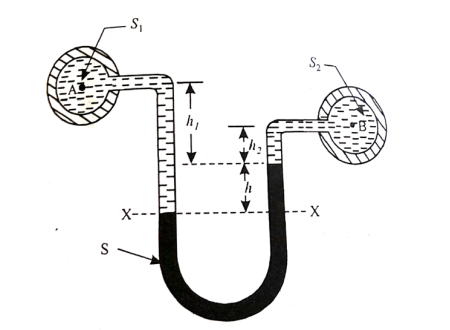
Fig no 8 Utube differential manometer
Let, h = difference of mercury level (heavy liquid) in the U-tube,
h1 = distance of the centre of A, from the mercury level in the left limb
h2 = distance of the centre of B, from the mercury level in the right limb,
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of heavy liquid o mercury
HA = pressure head at A,
HB = pressure head at B
Considering the pressure heads above the datum line x-x, we get
Pressure head in the left limb:
h A + ( h 1 + h ) S1
Pressure head in the right limb:
h B + h 2 × S 2 + h × S
Equating the above pressure heads, we get
h A + ( h1 + h ) S1 = h B + h 2 × S 2 + h× S
( h A - h B ) = h 2 × S 2 + h × S - ( h 1 + h ) S 1
Q7) Explain manometer?
A7)
- A micro manometer can be used - if required in combination with pitot tubes - to measure, measure, measure and calculate velocity and volumetric flow rate. Micro manometers have high accuracy for measuring high-, low- and variability. Observatory Instruments offer different micro manometers, each with a different application.
- One leg of the micro manometer is the source and the other is the inclined tube, which contains a magnifier. The meniscus in the inclined tube is located at a reliable level adjusted by the hairline viewed by the magnifier.
- First of all both the source and the amplifier are the same pressure. The application of pressure at the end of the spring removes the hairline but can be restored to its original position by increasing or lowering the source (mercury sump).

Fig no 9 Micro manometer
Q8) Explain pressure gauge?
A8)
Mechanical Gauges
- The manometers are suitable for comparatively low pressure.
- For high pressures, they become unnecessarily larger even when they are filled with heavy liquids.
- Therefore, for measuring medium and high pressures, we make use of elastic pressure gauges.
- They employ different forms of elastic systems such as tubes, diaphragms or bellows etc. to measure the pressure.
- The elastic deformation of these elements is used to show the effect of pressure. Since these elements are deformed within the elastic limit only, therefore these gauges are sometimes called elastic gauges.
Bourdon tube pressure gauge:
- Bourdon tube pressure gauge is used for measuring high as well as low pressure.
- In this case, the pressure element consists of a metal tube of approximately elliptical cross section.

Fig no 10 Bourdon tube pressure gauge
- This tube is bent in the form of a segment of a circle and responds to pressure changes.
- When one end of the tube which is attached to the gauge case, is connected to the source of pressure, the internal pressure causes the tube to expand, whereby circumferential stress is set up.
- The free end of the tube moves and is in turn connected by suitable levers to a rack, which engages with a small pinion mounted on the same spindle as the pointer.
- Thus the pressure applied to the tube causes the rack and pinion to move.
- The pressure is indicated by the pointer over a dial which can be graduated in a suitable scale.
- The Bourdon tube are generally made of bronze or nickel steel.
- The former is generally used for low pressures and the latter for high pressures.
Diaphragm Gauge:
- This type of gauge employs a metallic disc or diaphragm instead of a bent tube.
- This disc or diaphragm is used for actuating the indicated device.
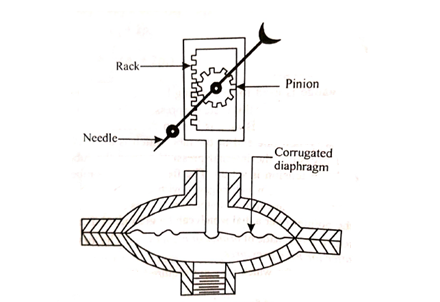
Fig no 11 Diaphragm gauge
- When pressure is applied on the lower side of the diaphragm it is deflected upward.
- This movement of the diaphragm is transmitted to a rack and pinion.
- The latter is attached to the spindle of needle moving on a graduated dial.
- The dial can again be graduated in a suitable scale.
Vacuum gauge:
- Bourdon gauges discussed earlier can be used to measure vacuum instead of pressure.
- Slight changes in the design are required in this purpose.
- Thus, in this case, the tube be bent inward instead of outward as in pressure gauges.
- Vacuum gauges are graduated in millimeters of mercury below atmospheric pressure.
- In such cases, therefore, absolute pressure in millimeters of mercury is the difference between barometer reading and vacuum gauge reading.
- Vacuum gauges are used to measure the vacuum in the condensers etc. If there is leakage, the vacuum will drop.
Q9) Explain hydrostatic pressure force like horizontal, vertical and inclined surface?
A9)
Fluid Statics
- Fluid Statics interacts with the relaxing fluid while Fluid Dynamics explores the flow fluid.
- Any improved power is caused only by normal pressure i.e., pressure. Such a condition is called hydrostatic condition.
- Fluid Statics is also known as Hydrostatics.
- The static fluid cannot have the shear strength to which it operates, and that any force between the liquid and the boundary must operate in a direct way across the boundary.
- As for the liquid at rest, the factor will be proportional. The total number of energy components in any direction will be zero. The sum of the times the power of an object at any point and should be zero.
- Inside the liquid, the pressure is the same at all points in all directions.
- The pressure on the wall of any ship is toward the wall
- The pressure due to the depth is P = ρgh, and is the same for any specific level of the connected liquid.
Fluid Pressure at a point
- If the liquid is dry, then the force acting on any area or area is unique to that area.
- If the force is present in each area of the same boundary, the pressure is said to be the same

Fig no 12 Hydrostatic force on surface
Pascal's Law of Pressure at a Point
- It states that the pressure or pressure somewhere in the static fluid (liquid rest) is equal in all directions. If the fluid does not move according to Pascal's law,
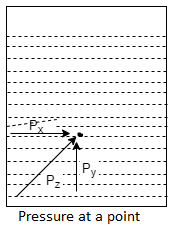
Fig no 13 Pressure at a point
Px = py = pz
Where, px, py and pz pressure point x, y, z respectively.
A typical equation of pressure variability in Static Fluid

Fig no 14 Pressure variability in static fluid
Dp / d s = -  g cos
g cos 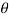
Vertical Variation of pressure in a fluid under gravity
Fig no 15 Vertical Variation of pressure in a fluid
Taking upward as positive, we have
Vertical cylindrical structure of a liquid body = A
Metal size = ρ
The force involved are:
- Force for p1 to A (top) = p1. A
- Force for p2 to A (bottom) = p2. A
- Forcing due to the weight of the material (bottom) = mg
= mass density x volume x g
= ρ.gA.A. (z2 - z1)
Thus in a liquid that is below gravity, the pressure decreases proportionally with the elevation
p2 - p1 = ρgA (z2 - z1)
This is a change in hydrostatic pressure.
Equilibrium of Pressure at Equivalent Static Fluid
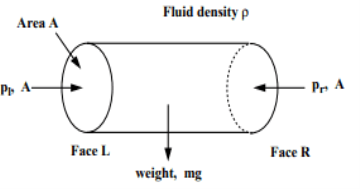
Fig no 16 Pressure act on horizontal surface
Horizontal element of cylindrical cross sectional area = A
Metal size = ρ
Left end pressure = pl
Right end pressure = pr
Equally, the total energy in direction x is zero = pl. A = pr. A
Pl = pr
Therefore, the pressure in the horizontal direction does not change.
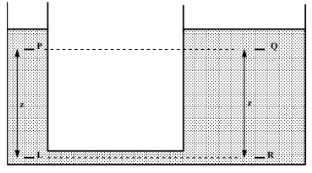
Fig no 17 Pressure in horizontal direction
As we know, P1 = pr

Therefore, the pressure at two equal levels is the same.
Total Hydrostatic Force in the Facial Area
- On the surface of a liquid plane submerged in a liquid, or in the airplane inside a gas chamber, or in another part of the aircraft under the same hydrostatic pressure, the total hydrostatic power is given by
F = p. A
Where p is the same pressure and A is the area.
- Generally, the total hydrostatic pressure in any aircraft area is equal to the local product output and the unit pressure at its center of gravity.
F = pcg. A
When the pcg pressure is in the center of gravity.
- To get the same free liquid at rest, the number can be displayed according to the unit weight γ of the liquid.
F = γh'A
Where h 'is the depth of the liquid above the centroid of the immersed area.
Q10) Explain buoyancy stability of floating bodies?
A10)
- Whenever a body is immersed wholly or partially in a fluid it is subjected to an upward force which tends to lift it up.
- The tendency for an immersed body to be lifted up in the fluid due to an upward force opposite to action of gravity is known as buoyancy.
- The force tending to lift up the body under such conditions is known as buoyant force or force of buoyancy.
- The magnitude of the buoyant force can be determined by Archimedes principle which states as follows:
- When a body is immersed in a fluid either wholly or partially it is buoyed or lifted up by a force which is equal to the weight of fluid displaced by the body.
Centre of Buoyancy
- The point of application of the force of buoyancy on the body is known as the center of buoyancy. It is always the center of gravity of the volume of fluid displaced.
Equilibrium of floating and submerged bodies
Stability of floating Body:
The stability of a floating body is determined from the position of Meta-centre (M).
a). Stable Equilibrium
- If the point M is above G, the floating body will be in stable equilibrium as shown in Fig.
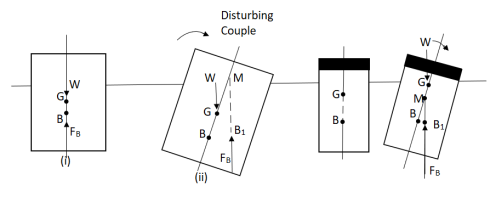
M is above G ( stable equilibrium ). M is below G ( unstable equilibrium )
Fig no 18 Stability of floating bodies
- If a slight angular displacement is given to the floating body in the clockwise direction, the center of buoyancy shifts from B to B1, such that the vertical line through B1 cuts at M.
- Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anti-clockwise direction and thus bringing the floating body in the original position.
b. Unstable Equilibrium:
- If the point M is below G, the floating body will be in unstable equilibrium as shown in fig.
- The disturbing couple is acting in the clockwise direction.
- The couple due to buoyant force FB and W is also acting in clock direction and thus overturning the floating body.
c. Neutral Equilibrium:
- If the point M is at the center of gravity of the body. The floating body will be in neutral equilibrium.
Stability of submerged Body:
- The position of center of gravity ¢er of buoyancy in case of a completely submerged body are fixed.
- Weight W acting vertically downward through G, while the buoyant force FB is acting vertical up through B.
Stable equilibrium :
When W = FB& point B is above G, the body is said to be in stable equilibrium.
Unstable Equilibrium :
If W = FB , but center of buoyancy B is below the center of gravity G, the body is in unstable equilibrium.
Neutral Equilibrium :
If W = FB & point B & G are at the same point, the body is said to be in neutral equilibrium.
Q11) Barometric reading at a place is 75 cm of Hg. Express the pressure intensity of 10 N per cm² is:
(1) m of water
(2) mm of mercury
(3) KN.m^2 abs
A11)
Given:

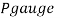 = 10 N/cm² = 100 kN/m².
= 10 N/cm² = 100 kN/m².
(i) In m of water,
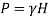
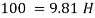
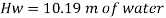
(ii) In mm of mercury

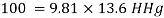
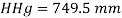
(iii) In kN/m absolute,
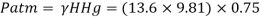
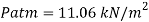
Absolute pressure,

Q12) A gauge on suction side of pump shows a negative pressure of 0.285 bar. Express this pressure in terms of
1. Pressure intensity kPa
2. N/m absolute
3. m of water gauge
4. m of oil (S0.85) absolute
5. Cm of mercury gauge.
Take atmospheric pressure as 76cm of mercury and relative density of mercury as 13.6.
A12)
1 bar = 10'^5 Pa
Gauge vacuum reading

Absolute pressure
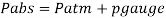

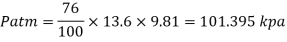

Equivalent head of water (gauge)
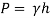

Equivalent head of oil (absolute)
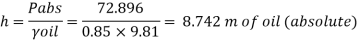
Head of mercury (gauge)
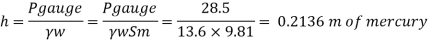

Q13) A cylinder contains a fluid at a gauge pressure of 350kPa. Express the pressure in terms of the column height of (a) water (o 1000kg/m) (b) Hg (S= 13.6). What would be absolute pressure in the cylinder if the atmospheric pressure is 101.3kPa?
A13)
Given:
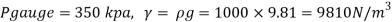
(a) Pressure in term column head of water,
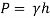

(b) Pressure head in terms of Hg
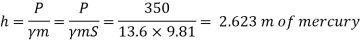
(c) Absolute Pressure
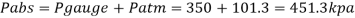
Q14) Mass density of a liquid varies as p = (1000+ 0.008 h). Where 'h' is depth (m) below free surface of liquid. Determine depth at which gauge pressure would be 100 kPa.
A14)
Given: 
To find: Depth?
Pressure at any point

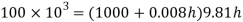

Q15) Measurements of pressure at the base and top of a mountain are 74cm and 60cm of mercury respectively. Workout the height of mountain if air has specific weight 11.97 N/m²
A15)
Pressure at top
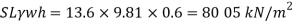
Pressure at bottom
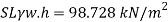


Q16) A piezo meter tube is fitted to a tank containing water at a point 600 mm above the tank. The liquid in the manometer is carbon bi Sulphide having a specific gravity of 1.9. Find the height of the free water surface above the bottom of the tank if the piezo meter reading 700 mm. Find also the pressure intensity at the bottom of the tank. Dec. 2005, 4 Marks
A16)
Pressure at end of piezometer

Height of water above point A
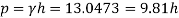
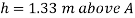
Height of free surface above bottom of tank
H = h +0.6
= 1.33 +0.6 = 1.93m
Pressure at bottom of tank

Q17) A piezometer tube is fitted to a tank containing water at a point 500 mm above the bottom of the tank. The liquid in the manometer is carbon tetrachloride (sp. Gr. 1.6). Find the height of the free water surface above the bottom of the tank if the piezometer reading is 600 mm. Find the pressure intensity at the bottom of the tank.
A17)
For static equilibrium

Pressure in the tank at point A= pressure due to piezometric liquid at A

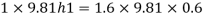
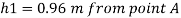
Total height of the free water surface above bottom of tank
h =h₁+0.5 = 0.96 + 0.5 = 1.46 m
Pressure intensity at the bottom of the tank

Q18) A simple U-tube manometer is used to measure water pressure in pipe line. The left limb of manometer connected to the pipe and the night limb is open to atmosphere. The mercury level in the left limb is 80mm below the center of the pipe and the level in the right limb in 220mm above the center of the pipe. Calculate the pressure of water in meter and also in km
A18)
Oil
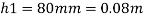
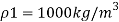
Mercury

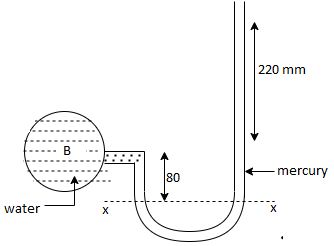

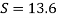
Pressure in the left limb about xx = Pressure in the right limb about x-s


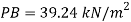
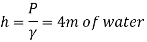
Q19) A U-tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The night limb of the manometer contains mercury and is open to atmosphere. The contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tule 12 cm and the free surface of mercury is in level with the centre of the pipe. It the pressure of water in pipe he is reduced to 9810 N/m². Calculate the new difference in the level of mercury.
A19)

Case I
Given:
h1,=h₂= 12cm=0.12 m.
S2=13.6
Pressure in pipe
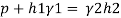
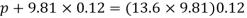

Case II
Since the pressure in the pipe is reduced to 9.81 kN/m² (which is less than 14.83 kN/m²), the mercury in the left limp will be rise. Rise of mercury in the left limb will be equal to the fall of mercury in right limb as the total volume of mercury remains same.
Let x = rise of mercury in left limb= fall in mercury in right limb,
Pressure at new section x₁ - x₁

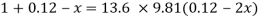
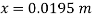
.. New difference of mercury
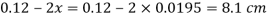
Q20) Fig. P shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer given in the Fig. P. 3.7.15 shows when the vessel is empty. Find the reading of the manometer when the vessel is completely filled with water.
A20)

Case I:
Vessel is empty
Pressure in left limb about x-x= Pressure in right limb about x-x

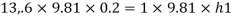
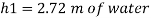
Case II: Vessel is full of water
When pressure is full of water, the pressure in right limb will increase and mercury level will fall by 'y' m, similarly Hg level in left limb will rise by 'y' m
Now consider 7-7 as a datum
Pressure in left limb = Pressure in right limb about z-z
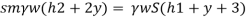

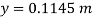
:. Difference of mercury level when the vessel is full of

Q21) A differential manometer is connected at two points A and B of two pipes as shown in Fig. Pipe A contains liquid of specific gravity 1.6, while pipe B contains liquid of specific gravity 0.8. If the pressure at A and B are 11.80 x 10 N/m² and 19.60 x 10 N/m2, find the difference in mercury level in the differential manometer.
A21)
Pipe A
S₁ = 1.6
PA = 11.8 x 10' N/m² = 118 kN/m² 19.62× 10¹ N/m² = 196.2 kN/m²
h₁ = (2+1,5) = 3.5 h₂ = (1.5 + h)
Pipe B
s2= 0.8
h2= 1.5+h
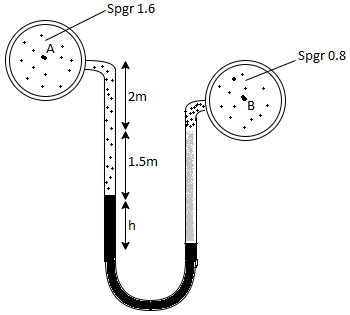
Pressure in left limb = pressure in right limb PA

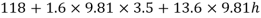
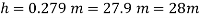
Q22) A U-tube manometer (Fig. P.) measures the pressure difference between two points A and B in a liquid of density PL The U tube contains mercury of density pa. Calculate the difference of pressure between points A and B in a liquid of density p, The u tube contains mercury of density P Calculate the difference of pressure between points A and B if the liquid contain at A is water take a 1.5 m, b=0.75 m and h= 0.50 m.
A22)
Given:


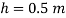

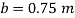
To find :
PA-PB
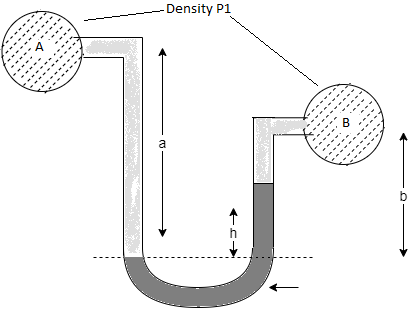
Pressure in left limb = Pressure in right limb

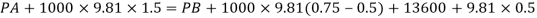
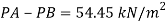
Q23) Liquid of specific gravity 1.0 flows through pipes A and B at positive pressures of 0.5 bar and 0.25 bar respectively. Pipe A is 1.8 m higher than B. What would be the difference in the levels of U-tube manometer connected to A and B, having manometric liquid of specific gravity 13.6 ? Liquid level in the limb attached to A is lower than that in the order.
A23)
Given:
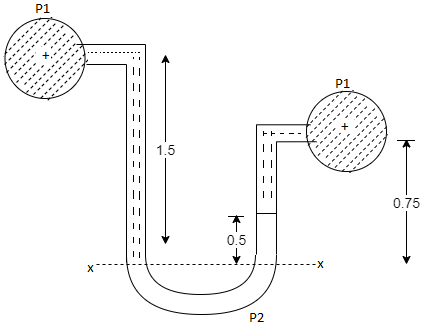
1 1bar = 10^5 N/m²,
2 P=0.5 bar = 50 kN/m².
3 pB= 0.25 bar 25 kN/m²
Balancing the liquid about x-x in left limb and right limb
Pressure in left limb about x-x= Pressure in right limb about x-x
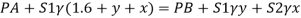

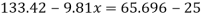
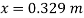
Q24) A pressure gauge, calibrated to read volume of fuel, is used as a fuel gauge. It is connected at the bottom of a fuel tank of area 267 cm². The gauge is calibrated to read maximum volume of 8 liters. If there accumulates 1 cm layer of water in the tank, how much fuel is measured when the gauge shows full scale reading? Assume density of fuel 730 kg/m².
A24)
Given:
Tank base Area A = 267 cm² = 267 x 10 m²
Max. Volume V = 8 liters = 8 x 10¹ m²
Density of fuel p₁ = 730 kg/m
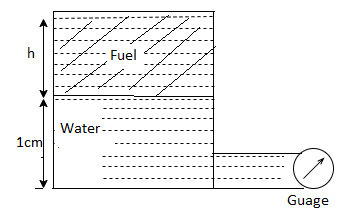
Depth of fuel for maximum volume
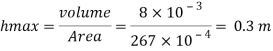
Max. Pressure for which gauge is calibrated
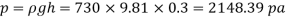
Total pressure due to water + Pressure due to fuel

Volume of fuel

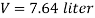
For full scale reading, volume of fuel is 7.64 liter
Q25) Gauge A attached at the bottom of a tank shown in Fig. P. 3.7.7 reads 350 kPa (absolute). What is the height 'h' of water? What is the reading of gauge B?
A25)
Given:
P = 350 (absolute)
Pressure due to mercury
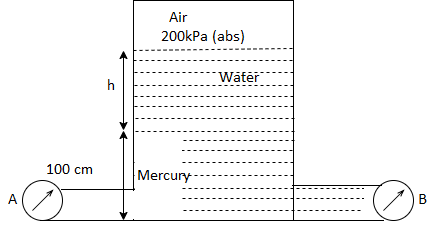

Consider pressure from A up to air
Let 'h' be the height of water
Height of water is 1.69 m
Now consider pressure from air up to gauge B Let P be the gauge pressure at B
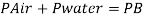

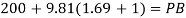
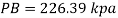
Pressure at B is 226.39 kPa (abs)
Q26) A 6 m deep tank contains 4 m of water and 2 m of oil of relative density 0.8. Determine the pressure at the bottom of the tank.
A26)
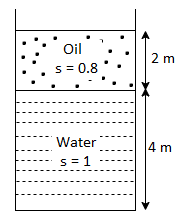
Specific weight
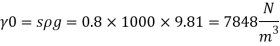
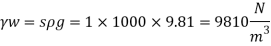
Q27) A closed tank of height 9.0 m is filled with bromine of specific gravity 3.1 to a depth of 2 m and turpentine of specific gravity 0.87 to a depth of 6m. The upper part of the tank contains air under a pressure of 25 kPa (vacuum). Find the absolute pressure at the bottom of the tank in kPa and in cm of mercury Neglect density of air. Consider atmospheric pressure 101.3 kPa.
A27)
Given:
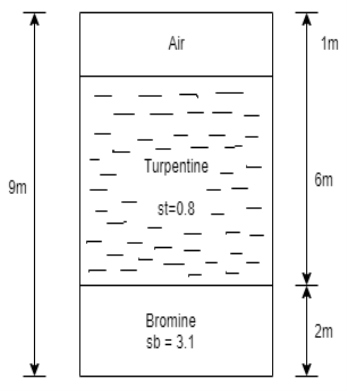
Atmospheric pressure
Patm= 101.3 kpa
Air pressure P=25 kPa (vacuum)
Gauge pressure at bottom of tank
= Air pressure + pressure due to turpentine + pressure due to bromine
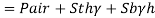


Absolute pressure

Pressure head in term mercury
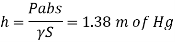
Q28) The tank shown in Fig. P. Is closed at to and contains air at a pressure of P, Calculate the value of P, for the manometer reading as shown in Fig.
A28)
Given:
h₁ = 10 cm = 0.1 m,
h₂ = 150 cm= 15m
h3 = 200+10-150=60 cm=0.6 m
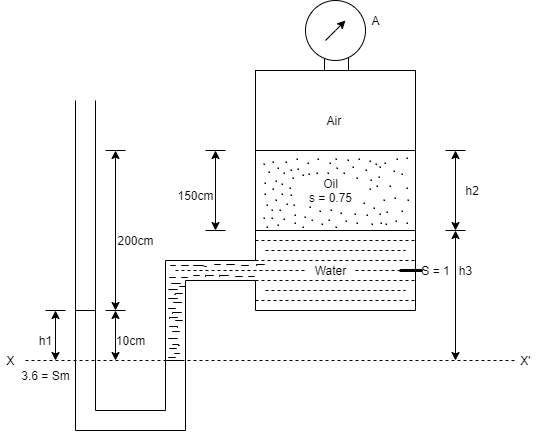
Consider section X-X, balance the fluid about X-X.
Pressure on left limb about XX= Pressure on right limb about X-X
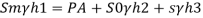


Q29) A vertical rectangular plane surface has width of 1.5 m and depth of 3.0 m. It is placed in water such that the upper edge is 1 m below free water surface. Find the total pressure and the depth of centre of pressure on the rectangular plane.
A29)
Given:
b= 1.5 m,
d = 3.0 m 1m,
s = 1 (water)

To find: P and h
Area A = b x d=1.5x3=4.5 m²
Distance of centroid of lamina from free surface,

Total of inertia
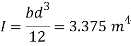
Total pressure,
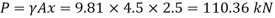
Centre of pressure,
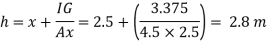
Q30) A rectangular gate 2 m long and 1.5 m wide lies in a vertical plane with its centre 2.5 m below water surface. Calculate magnitude, direction and location of the total force on the gate.
A30)
Given:
x=2.5m, b = 2m, d=1.5m
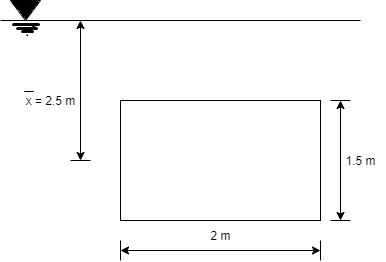
To find
P and h
Moment of inertia
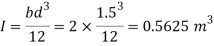
Total pressure
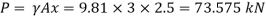
Centre of pressure

Q31) An isosceles triangular plate of base band altitude 'h' meter is immersed vertically in water with its apex below the base. The base is parallel to and vertical depth of 'd below free surface. Prove that the depth of pressure is equal to (h²-4dh+6d²)/ (3d+h)
A31)

Distance of centroid from free surface
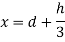
Area of triangle,

Moment of inertia
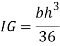
Centre of pressure
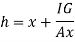

Q32) A circular plate 2.95 m diameter is immersed in water in such a way that its greatest and least depth below the free surface is 4.1 m and 1.6 m respectively. Determine the total pressure on one face of the plate and position of center of pressure.
A32)
Given:
d=2.95 m,
Least depth 1.6 m,
Greatest depth 4.1 m

To Find: P and h
Area of plate

Moment of inertia
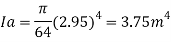
Distance of c. g. Of plate from free surface
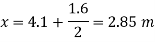
1. Total pressure, p
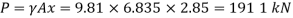
2. Position of center of pressure, h
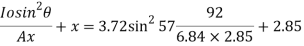
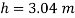
Q33) A square plate 6 m x 6 m is placed in a liquid of specific gravity 0.8 at an angle of 30 with free liquid surface. A square hole 1.5 m in size is cut exactly in the center of the plate. Its greatest and the least depths below the free liquid surface are 4 m and 2 m respectively. Determine the total pressure on one face of the plate and position of center of pressure.
A33)
Given: S=0.8, 0=30°
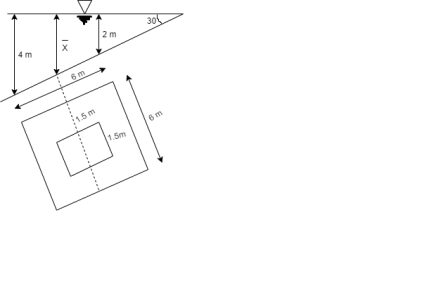
To Find: P and h
Area A=6²-1.5 = 33.75 m²
Position of centroid of lamina from free surface

Moment of inertia,

Total pressure,

Q34) A solid cube of sides 0.5 m each is made of material of relative density 0.5. Tho cube floats in a liquid of relative density 0.95 with two of its faces horizontal. Examine its stability.
A34)
Given:
Side a=0.5 m
Relative density 0.5 m
Relative density of cube Sc= 0.5
Relative density of liquid S₁ = 0.95
Weight of cube = Weight of liquid displaced
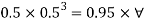
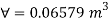
Depth of immersion (h).
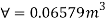
Depth of immersion (h),
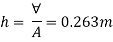
Distance of C.G. From O.
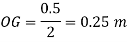
Distance of buoyancy from O.
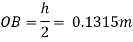
Now, BG= OG-OB=0.25-0.1315 = 0.1185 m

Metacentric height, BM-BG

Negative sign of metacentric height indicates that in unstable equilibrium.
Q35) A rectangular pontoon is 5 m long, 3 m wide and 1.20 m high. The depth of immersion of the pontoon is 0.80 m in sea water. If the centre of gravity is 0.6 m above the bottom of the pontoon, determine the metacentric height. The density for sea water = 1025 kg/m².
A35)
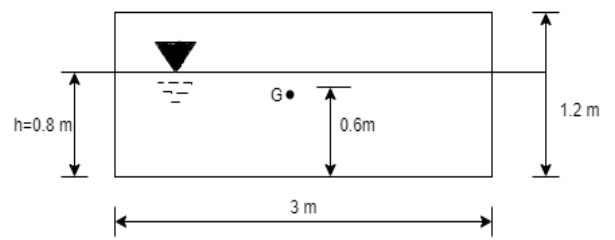
Volume of liquid displaced
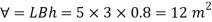
Moment of inertia

Metacentric height BM BG=