Unit - 6
Dimensional Analysis and Hydraulic Similitude
Q1) Explain Buckingham pi method?
A1)
- When a large number of physical variables are involved Rayleigh’s method of dimensional analysis becomes increasingly laborious and cumbersome.
- Buckingham’s method is an improvement over the Rayleigh’s method.
- Buckingham’s designated the dimensionless group by the letter Π. It is therefore often called Buckingham Π-Method.
- The Buckingham’s Π-Method states as follows:
“If there are n variables in a dimensionally homogeneous equation and if these variables contain fundamental dimensions (such as M, L, T, etc.) then the variables are arranged into (n-m) dimensionless terms.
- These dimensionless terms are called Π– terms.”
Mathematically, if any variable X1, depends on independent variables, X2, X3, X4,…… Xn; the functional equation may be written as
 -------- 1
-------- 1
Equation 1 can also be written as
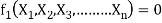 -------- 2
-------- 2
It is dimensionally homogeneous equation and contains n variables.
If there are m fundamental dimensions, then according to Buckingham’s Π – theorem, it [equation] can be written in terms of number of Π – terms in which number of Π terms is equal to (n-m).
Hence equation 2 becomes as
 --------3
--------3
Each dimensionless 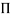 – term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
– term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
These m variables which appear repeated in each of  – terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
– terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
Let in the above case X2, X3 and X4 are the repeating variables if the fundamental dimensions m(M, L, T) = 3, then each term is written as:
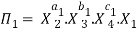

.
.
.
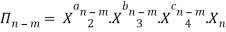 -------- 4
-------- 4
Where a1, b1, c1, a2, b2, c2 etc. are the constants, which are determined by considering dimensional homogeneity. These values are substituted in equation 4 and values of  are obtained. These values of Π’s are substituted in equation 3.
are obtained. These values of Π’s are substituted in equation 3.
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:
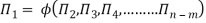
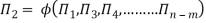
Q2) Explain the term Reynold Number.
A2)
Reynolds number
- Reynolds (Re) number helps to predict flow patterns in various fluid flow conditions. In low Reynolds numbers, the flow is usually dominated by laminar (sheet-like) flow, while at high Reynolds numbers the flow is often chaotic.
- Confusion is caused by variations in the speed of the curve and direction, which can sometimes combine or incite opposition to the full flow direction (eddy currents). These eddy currents begin to compress the flow, applying energy to the process, which in turn increases the chances of explosion. Reynolds numbers are immeasurably important for liquid mechanics.
- Reynolds number has a wide range of applications, ranging from the liquid flow of the pipe to the air flow over the wing of the aircraft. It is used to predict the transition from laminar to turbulent travel, and is used to measure the same flow conditions but with different sizes, such as between aircraft model in the air tunnel and a full-size version.
- Early predictor of turbulence and the ability to calculate the measurement results can be used to help predict liquid performance at a larger scale, such as in air and ground or water movement and thus to have climate-related and climate-related results.
- Reynolds number is a measure of the weak energy and viscous energy within a fluid that affects the corresponding internal movements due to the different velocities of the fluid. The region in which this force changes function is known as the boundary membrane, as the surface is enclosed within a pipe.
- The same effect is achieved by introducing high-velocity fluid currents into low-velocity fluid, like hot gases emitted by flames in the air. The movement associated with this creates a liquid tension, which is a factor in promoting turbulent flow.
- The opposite of this effect is the viscosity of the fluid, which usually prevents turbulence. Reynolds' number measures the relative importance of these two types of energy in the given flow conditions, and is an indication of when the turbulent flow will occur in a given situation.
- This ability to predict the onset of flow flows is an important invention of mechanical devices such as plumbing or wing systems, but Reynolds' number is also used to measure dynamic water problems, and is used to determine the dynamic similarity between two different fluids, such as between a model aircraft, and its full version.
- Such measurements are not online and the use of Reynolds numbers in both cases allows for enhanced rating features.
With respect to laminar and turbulent flow regimes:
- Laminar flow occurs with low Reynolds numbers, in which viscous forces are prominent, and are characterized by smooth, consistent movements;
- Turbulent flow occurs at high Reynolds numbers and is dominated by weak forces, often producing eddy, turbulence and other flow conflicts.
Reynolds' number is described as
Re = u L / 
Where:
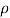 is the humidity (SI units: kg / m3)
is the humidity (SI units: kg / m3)
u is flow speed (m / s)
L different line size (m) (see paragraphs below this article for examples)
μ is the strong viscosity of the fluid (Pa · s or N · s / m2 or kg / (m · s))
 is the kinematic viscosity of fluid (m2 / s).
is the kinematic viscosity of fluid (m2 / s).
- Reynolds' number can be defined in a variety of situations where the fluid is a facial-related movement.
- These definitions usually include liquid properties of mass and viscosity, as well as the velocity and length of the element or the size of the element (L in the above figure). This size is a matter for the meeting - for example radius and scope work equally well to define sections or circles, but one is chosen by the meeting. On planes or ships, length or width can be used.
- The flow of the pipe, or liquid-moving phase, the internal diameter is widely used today. Other shapes such as rectangular pipes or non-circular objects have the same specified width. For liquefaction fluids such as compressed gases or fluid viscosity fluids such as non-Newtonia fluids, special rules apply. Speed can also be a matter of assembly in some cases, especially for renewable vessels.
- In practice, matching Reynolds' number is not enough in itself to ensure consistency. The flow of fluid is usually chaotic, and very small changes in the shape and appearance of the surface of the conjunctiva can lead to very different flow. However, Reynolds numbers are a very important guide and are widely used.
Q3) An oil of specific gravity 0.9 and viscosity 0.9 poise is to be transported at the rate of 1000 l/s through a. 1.2 m diameter pipe. Tests were conducted on a 10 cm diameter pipe using water at .20°C. Viscosity of water at 20°C is 0.01 poise. Find the rate of flow in the model.
A3)
Prototype
D = 1.2 m.
Sp = 0.9,
Model
Dm = 10 cm = 0.1 m
Sm = 1
μp = 0.9 poise. μm = 0.01 poise = 1 x 10-² poise
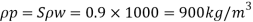
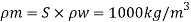
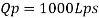
To find: Velocity and flow rate.
Since it is pipe flow, Reynolds’s number must be applied.
(Re)model = (R) prototype






Rate of flow through model
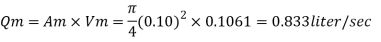
Q4) From the following data, find the scale ratio of model Velocity of water 1 m/'s through circular pipe. Prototype: Velocity of oil 0.12 ms through 50 mm diameter pipe. Assume kinematic viscosity of water 0.01 cms and that of oil 0.008 cm/s. Assume dynamic similarity. Also find the diameter of pipe used for model.
A4)
Prototype
Vp -012 m/s
Dp = 50mm = 0.05 m
Vp = 0.006 cm²/sec
Model
Vm= 1m/s
Dm=?
Vm= 0.01 cm^2/sec
To find:
Since it is pipe flow, Reynold's ember mast be applied
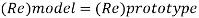

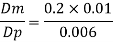


Model scale ratio is 1:5
Now, diameter of model pipe
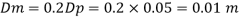
Q5) Water at 15.6°C flows at 3.5 m/s in a 150 mm diameter pipe. At what velocity must a fuel oil at 32.6°C flow in a 75 mm diameter pipe for the flow to be dynamic similar? v.-1.13 x 10 m/s and 2.96 x 10 m/s.
A5)
Water
Dw = 150 mm = 0.15 m
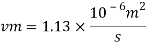
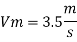
Oil
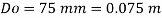

To find: Velocity of oil V.
Since it is pipe flow, Reynold's number must be applied
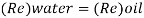
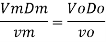

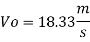
The velocity of cl at 32.6°C is 15.33 m'k
Q6) A ship has a length of 150 m and wetted area 3000 m² A model of this ship 5 m in length when towed in fresh water (p= 1000 kg/m) at 2 m/s produces a resistance of 40N. Calculate (1) corresponding speed of the ship. (i) the shaft power required to propel the ship at this speed through sea water (p=1030 kg/m). Take the propeller efficiency as 75%
A6)
Model
Lm= 5 m

Vm= 2 m/s
Fm = 40 N
Prototype
Lp= 150 m
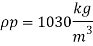
Ap= 3000m^2
Propeller efficiency= n= 75 %
To find:
Speed of ship Vp
Since it is ship motion Reynolds number must be applied



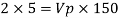
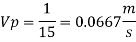
Ratio of drag force
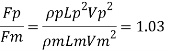
Drag force on prototype
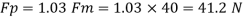

Actual power input
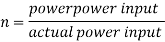

Q7) A ship 300 m long moves in seawater whose density is 1030 kg/m A1.75 Model of this ship is to be tested in a wind tunnel. The velocity of air in wind tunnel is 29 m/s the resistance of the model is 60 N. Determine velocity and resistance of the ship in seawater. Air density is 1.24 kg/m Kinematic viscosity of air=0.018 stokes Kinematic viscosity of seawater 0,01 stokes.
A7)
Given:
Prototype
Scale 1:75
Lp = 300 m
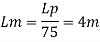
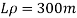


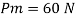

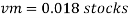
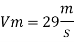
To find:
Vp and Fp
Since it is ship motion Reynolds number must be applied

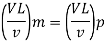

Drag force ratio
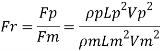
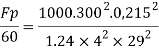
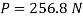
Q8) In a geometrically similar model of weir the discharge is 0.15 m².s.. if the scale of the model is 1/50 find the discharge of the prototype.
A8)
Given:
Discharge per meter length = 0.15 m/sec.
Scale ratio Lr = Lp/Lm = 50
To find: qp
Since it is a spillway, Froude Number must be applicable.
The discharge ratio for spillway is given by
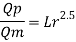
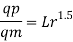

Q9) The performance of a spillway is to be studied by means of a model constructed to a scale of 1:9. Determine: (1) Rate of flow in the model for a prototype discharge of 1400 m/s. (2) Energy lost in the prototype if the energy loss in model is 0.3 kW
A9)
Given:
Scale of model 1:9
Lr = 9
Discharge of proto type Q = 1400 m^3 /s
Since it is a spillway, Froude number must be applicable.
Using discharge scale ratio
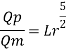
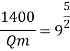

Energy loss
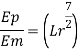

Q10) In the model test of a spillway the discharge per meter length is 1/6 m^3/sec if the scale of the model is 1/36 find the discharge per meter run of the prototype.
A10) Given:
Qm = 1/6 m^3/sec
Lr = Lp/Lm = 36
To find: QP
Since it is a spillway, Froude Number must be applicable. The discharge ratio for spillway is given by
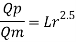


Q11) Find the suitable scale for model of a spillway if maximum discharge available in the laboratory is 10 L.P.S. And the prototype discharge is 168.07 m/sec.
A11)
Given:
Q=10 lps = 10 x10³ m³/sec;
Qp = 168.07 m^3/sec
Since it is a spillway, Froude Number must be applicable. Using discharge scale ratio

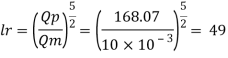
Model scale should be 1:49.
Q12) A ship model of scale 1/60 is towed through sea water at a speed of 1:1 m/s A force of 2.1 N is required to tow the model. Determine the speed of ship and the propulsive force on the ship if the prototype is subjected to wave resistance only.
A12)
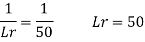
Speed of model Vm=1.1 m/s

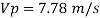
Resistance to prototype in sea water
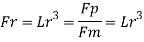

Q13) Explain the terms:
- Froude number
- Mach number
- Weber number
- Euler number
A13)
Froude number
Froude’s number, Fr, is an infinite number that describes the various states of open channel flow. Froude's number is a measure of gravity and gravity.
Gravity (number) - moves water down
Inertia (denominator) - shows its willingness to do so.
Fr = v / √ (g D)
Where:
V = Water speed
D = Hydraulic depth (flow area / over width)
g = Gravity
When:
Fr = 1, critical flow
Fr> 1, basic flow (fast flow)
Fr <1, poor flow (slow / silent)
- Froude's number is the measure of the flow signals such as waves, sand formation, flow / depth of contact in the cross section or between large rocks.
- The denominator represents the slower wave surface on the surface of water compared to the speed of the water, called wave celerity. In the flow of critical flow is similar to the flow of speed. Any facial distortion will remain standing. In a continuous flow the flow is controlled from below and the information is transmitted above. This condition leads to post-water effects. Excellent flow is controlled upwards and disturbances are transmitted downstream.
- Wave propagation can be used to illustrate these flow conditions: A stick placed in water will form a V-wave pattern below. If the flow is small waves will appear in front of the rod. If the flow is a critical wave it will have a 45o angle. If the flow is excessive the rising waves will appear and the wave angle will be below 45°.
Mach number
Mach (M or Ma) number is an infinite magnitude in the force of a liquid that represents the rate of flow rate beyond the local speed limit.
M = u / c
Where: M local Mack number,
u is the local velocity flow in relation to boundaries (either internal, such as something flow-focused, or external, as a channel), and
c is the speed of the sound in the middle, in the air which varies with the square root of the thermodynamic temperature.
- By definition, in March 1, the local flow speed is equal to the speed of the sound. In March 0.65, 65% is subsonic speed, and, on March 1.35, 35% is faster than supersonic speed.
- Pilots who use high-performance aircraft use the aircraft number to indicate the actual air conditioning of the vehicle, but the flow path around the vehicle varies in size by three, depending on the local area number.
- The local speed of the noise, which is why Mach's number also depends on the temperature of the surrounding gas. Mach number is used primarily to determine the limitations at which the flow can be treated as an inconsistent flow.
- The contents can be gas or liquid. The boundary can move in the middle, or it can be set while the center is flowing, or they can both go, at different speeds: what matters is their relative relative speed.
- A boundary can be the boundary of an object centered on an internal object, or a channel such as a microphone, design or air channel that transmits a medium. Since Mach's number is defined as a two-speed ratio, it is an infinite number.
- If M <0.2-0.3 and the flow are not too volatile and visually impaired, the reduction results will be smaller and easier to measure the flow rate can be used.
Weber number
Weber (We) is a flawless number for liquid technologies that are often useful in analyzing fluid flow where there is a connection between two different liquids, especially multiphase flow with tightly curved surfaces. Named by Moritz Weber (1871–1951).
It can be considered as a measure of the relative importance of fluid inertia compared to groundwater. The quantity helps to test the small flow of the film and the formation of droplets and bubbles.
Euler number
In the statistics, the Euler numbers sequence En numbers (A122045 sequence in OEIS) described the extension of the Taylor series
1/ cosh t = 2 / et + e-t
Where cosh t is hyperbolic cosine. Euler numbers are associated with a specific number of Euler polynomials, namely:
E n = 2 n E n (1/ 2)
Euler's numbers come from the growing series of Taylor's secretive and hyperbolic secant activities. The latter is a function in the definition. They also appear in combinations, especially when calculating the number of exchange permissions for a set with a number of items.
Unit - 6
Dimensional Analysis and Hydraulic Similitude
Q1) Explain Buckingham pi method?
A1)
- When a large number of physical variables are involved Rayleigh’s method of dimensional analysis becomes increasingly laborious and cumbersome.
- Buckingham’s method is an improvement over the Rayleigh’s method.
- Buckingham’s designated the dimensionless group by the letter Π. It is therefore often called Buckingham Π-Method.
- The Buckingham’s Π-Method states as follows:
“If there are n variables in a dimensionally homogeneous equation and if these variables contain fundamental dimensions (such as M, L, T, etc.) then the variables are arranged into (n-m) dimensionless terms.
- These dimensionless terms are called Π– terms.”
Mathematically, if any variable X1, depends on independent variables, X2, X3, X4,…… Xn; the functional equation may be written as
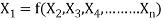 -------- 1
-------- 1
Equation 1 can also be written as
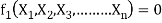 -------- 2
-------- 2
It is dimensionally homogeneous equation and contains n variables.
If there are m fundamental dimensions, then according to Buckingham’s Π – theorem, it [equation] can be written in terms of number of Π – terms in which number of Π terms is equal to (n-m).
Hence equation 2 becomes as
 --------3
--------3
Each dimensionless  – term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
– term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
These m variables which appear repeated in each of 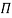 – terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
– terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
Let in the above case X2, X3 and X4 are the repeating variables if the fundamental dimensions m(M, L, T) = 3, then each term is written as:


.
.
.
 -------- 4
-------- 4
Where a1, b1, c1, a2, b2, c2 etc. are the constants, which are determined by considering dimensional homogeneity. These values are substituted in equation 4 and values of  are obtained. These values of Π’s are substituted in equation 3.
are obtained. These values of Π’s are substituted in equation 3.
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:
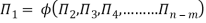

Q2) Explain the term Reynold Number.
A2)
Reynolds number
- Reynolds (Re) number helps to predict flow patterns in various fluid flow conditions. In low Reynolds numbers, the flow is usually dominated by laminar (sheet-like) flow, while at high Reynolds numbers the flow is often chaotic.
- Confusion is caused by variations in the speed of the curve and direction, which can sometimes combine or incite opposition to the full flow direction (eddy currents). These eddy currents begin to compress the flow, applying energy to the process, which in turn increases the chances of explosion. Reynolds numbers are immeasurably important for liquid mechanics.
- Reynolds number has a wide range of applications, ranging from the liquid flow of the pipe to the air flow over the wing of the aircraft. It is used to predict the transition from laminar to turbulent travel, and is used to measure the same flow conditions but with different sizes, such as between aircraft model in the air tunnel and a full-size version.
- Early predictor of turbulence and the ability to calculate the measurement results can be used to help predict liquid performance at a larger scale, such as in air and ground or water movement and thus to have climate-related and climate-related results.
- Reynolds number is a measure of the weak energy and viscous energy within a fluid that affects the corresponding internal movements due to the different velocities of the fluid. The region in which this force changes function is known as the boundary membrane, as the surface is enclosed within a pipe.
- The same effect is achieved by introducing high-velocity fluid currents into low-velocity fluid, like hot gases emitted by flames in the air. The movement associated with this creates a liquid tension, which is a factor in promoting turbulent flow.
- The opposite of this effect is the viscosity of the fluid, which usually prevents turbulence. Reynolds' number measures the relative importance of these two types of energy in the given flow conditions, and is an indication of when the turbulent flow will occur in a given situation.
- This ability to predict the onset of flow flows is an important invention of mechanical devices such as plumbing or wing systems, but Reynolds' number is also used to measure dynamic water problems, and is used to determine the dynamic similarity between two different fluids, such as between a model aircraft, and its full version.
- Such measurements are not online and the use of Reynolds numbers in both cases allows for enhanced rating features.
With respect to laminar and turbulent flow regimes:
- Laminar flow occurs with low Reynolds numbers, in which viscous forces are prominent, and are characterized by smooth, consistent movements;
- Turbulent flow occurs at high Reynolds numbers and is dominated by weak forces, often producing eddy, turbulence and other flow conflicts.
Reynolds' number is described as
Re = u L / 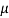
Where:
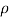 is the humidity (SI units: kg / m3)
is the humidity (SI units: kg / m3)
u is flow speed (m / s)
L different line size (m) (see paragraphs below this article for examples)
μ is the strong viscosity of the fluid (Pa · s or N · s / m2 or kg / (m · s))
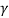 is the kinematic viscosity of fluid (m2 / s).
is the kinematic viscosity of fluid (m2 / s).
- Reynolds' number can be defined in a variety of situations where the fluid is a facial-related movement.
- These definitions usually include liquid properties of mass and viscosity, as well as the velocity and length of the element or the size of the element (L in the above figure). This size is a matter for the meeting - for example radius and scope work equally well to define sections or circles, but one is chosen by the meeting. On planes or ships, length or width can be used.
- The flow of the pipe, or liquid-moving phase, the internal diameter is widely used today. Other shapes such as rectangular pipes or non-circular objects have the same specified width. For liquefaction fluids such as compressed gases or fluid viscosity fluids such as non-Newtonia fluids, special rules apply. Speed can also be a matter of assembly in some cases, especially for renewable vessels.
- In practice, matching Reynolds' number is not enough in itself to ensure consistency. The flow of fluid is usually chaotic, and very small changes in the shape and appearance of the surface of the conjunctiva can lead to very different flow. However, Reynolds numbers are a very important guide and are widely used.
Q3) An oil of specific gravity 0.9 and viscosity 0.9 poise is to be transported at the rate of 1000 l/s through a. 1.2 m diameter pipe. Tests were conducted on a 10 cm diameter pipe using water at .20°C. Viscosity of water at 20°C is 0.01 poise. Find the rate of flow in the model.
A3)
Prototype
D = 1.2 m.
Sp = 0.9,
Model
Dm = 10 cm = 0.1 m
Sm = 1
μp = 0.9 poise. μm = 0.01 poise = 1 x 10-² poise

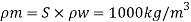

To find: Velocity and flow rate.
Since it is pipe flow, Reynolds’s number must be applied.
(Re)model = (R) prototype
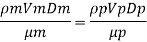

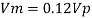


Rate of flow through model

Q4) From the following data, find the scale ratio of model Velocity of water 1 m/'s through circular pipe. Prototype: Velocity of oil 0.12 ms through 50 mm diameter pipe. Assume kinematic viscosity of water 0.01 cms and that of oil 0.008 cm/s. Assume dynamic similarity. Also find the diameter of pipe used for model.
A4)
Prototype
Vp -012 m/s
Dp = 50mm = 0.05 m
Vp = 0.006 cm²/sec
Model
Vm= 1m/s
Dm=?
Vm= 0.01 cm^2/sec
To find:
Since it is pipe flow, Reynold's ember mast be applied
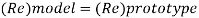

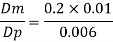

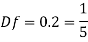
Model scale ratio is 1:5
Now, diameter of model pipe
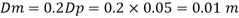
Q5) Water at 15.6°C flows at 3.5 m/s in a 150 mm diameter pipe. At what velocity must a fuel oil at 32.6°C flow in a 75 mm diameter pipe for the flow to be dynamic similar? v.-1.13 x 10 m/s and 2.96 x 10 m/s.
A5)
Water
Dw = 150 mm = 0.15 m
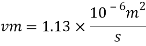
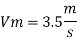
Oil
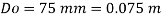
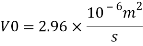
To find: Velocity of oil V.
Since it is pipe flow, Reynold's number must be applied
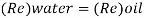
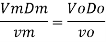
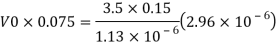
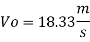
The velocity of cl at 32.6°C is 15.33 m'k
Q6) A ship has a length of 150 m and wetted area 3000 m² A model of this ship 5 m in length when towed in fresh water (p= 1000 kg/m) at 2 m/s produces a resistance of 40N. Calculate (1) corresponding speed of the ship. (i) the shaft power required to propel the ship at this speed through sea water (p=1030 kg/m). Take the propeller efficiency as 75%
A6)
Model
Lm= 5 m

Vm= 2 m/s
Fm = 40 N
Prototype
Lp= 150 m
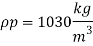
Ap= 3000m^2
Propeller efficiency= n= 75 %
To find:
Speed of ship Vp
Since it is ship motion Reynolds number must be applied


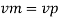

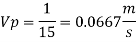
Ratio of drag force
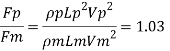
Drag force on prototype

Actual power input

Q7) A ship 300 m long moves in seawater whose density is 1030 kg/m A1.75 Model of this ship is to be tested in a wind tunnel. The velocity of air in wind tunnel is 29 m/s the resistance of the model is 60 N. Determine velocity and resistance of the ship in seawater. Air density is 1.24 kg/m Kinematic viscosity of air=0.018 stokes Kinematic viscosity of seawater 0,01 stokes.
A7)
Given:
Prototype
Scale 1:75
Lp = 300 m

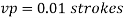
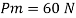

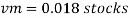

To find:
Vp and Fp
Since it is ship motion Reynolds number must be applied
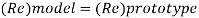


Drag force ratio



Q8) In a geometrically similar model of weir the discharge is 0.15 m².s.. if the scale of the model is 1/50 find the discharge of the prototype.
A8)
Given:
Discharge per meter length = 0.15 m/sec.
Scale ratio Lr = Lp/Lm = 50
To find: qp
Since it is a spillway, Froude Number must be applicable.
The discharge ratio for spillway is given by

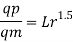
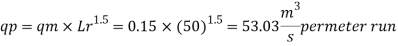
Q9) The performance of a spillway is to be studied by means of a model constructed to a scale of 1:9. Determine: (1) Rate of flow in the model for a prototype discharge of 1400 m/s. (2) Energy lost in the prototype if the energy loss in model is 0.3 kW
A9)
Given:
Scale of model 1:9
Lr = 9
Discharge of proto type Q = 1400 m^3 /s
Since it is a spillway, Froude number must be applicable.
Using discharge scale ratio
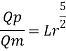
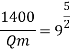
Energy loss

Q10) In the model test of a spillway the discharge per meter length is 1/6 m^3/sec if the scale of the model is 1/36 find the discharge per meter run of the prototype.
A10) Given:
Qm = 1/6 m^3/sec
Lr = Lp/Lm = 36
To find: QP
Since it is a spillway, Froude Number must be applicable. The discharge ratio for spillway is given by


Q11) Find the suitable scale for model of a spillway if maximum discharge available in the laboratory is 10 L.P.S. And the prototype discharge is 168.07 m/sec.
A11)
Given:
Q=10 lps = 10 x10³ m³/sec;
Qp = 168.07 m^3/sec
Since it is a spillway, Froude Number must be applicable. Using discharge scale ratio

Model scale should be 1:49.
Q12) A ship model of scale 1/60 is towed through sea water at a speed of 1:1 m/s A force of 2.1 N is required to tow the model. Determine the speed of ship and the propulsive force on the ship if the prototype is subjected to wave resistance only.
A12)

Speed of model Vm=1.1 m/s
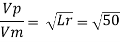

Resistance to prototype in sea water
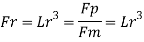
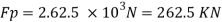
Q13) Explain the terms:
- Froude number
- Mach number
- Weber number
- Euler number
A13)
Froude number
Froude’s number, Fr, is an infinite number that describes the various states of open channel flow. Froude's number is a measure of gravity and gravity.
Gravity (number) - moves water down
Inertia (denominator) - shows its willingness to do so.
Fr = v / √ (g D)
Where:
V = Water speed
D = Hydraulic depth (flow area / over width)
g = Gravity
When:
Fr = 1, critical flow
Fr> 1, basic flow (fast flow)
Fr <1, poor flow (slow / silent)
- Froude's number is the measure of the flow signals such as waves, sand formation, flow / depth of contact in the cross section or between large rocks.
- The denominator represents the slower wave surface on the surface of water compared to the speed of the water, called wave celerity. In the flow of critical flow is similar to the flow of speed. Any facial distortion will remain standing. In a continuous flow the flow is controlled from below and the information is transmitted above. This condition leads to post-water effects. Excellent flow is controlled upwards and disturbances are transmitted downstream.
- Wave propagation can be used to illustrate these flow conditions: A stick placed in water will form a V-wave pattern below. If the flow is small waves will appear in front of the rod. If the flow is a critical wave it will have a 45o angle. If the flow is excessive the rising waves will appear and the wave angle will be below 45°.
Mach number
Mach (M or Ma) number is an infinite magnitude in the force of a liquid that represents the rate of flow rate beyond the local speed limit.
M = u / c
Where: M local Mack number,
u is the local velocity flow in relation to boundaries (either internal, such as something flow-focused, or external, as a channel), and
c is the speed of the sound in the middle, in the air which varies with the square root of the thermodynamic temperature.
- By definition, in March 1, the local flow speed is equal to the speed of the sound. In March 0.65, 65% is subsonic speed, and, on March 1.35, 35% is faster than supersonic speed.
- Pilots who use high-performance aircraft use the aircraft number to indicate the actual air conditioning of the vehicle, but the flow path around the vehicle varies in size by three, depending on the local area number.
- The local speed of the noise, which is why Mach's number also depends on the temperature of the surrounding gas. Mach number is used primarily to determine the limitations at which the flow can be treated as an inconsistent flow.
- The contents can be gas or liquid. The boundary can move in the middle, or it can be set while the center is flowing, or they can both go, at different speeds: what matters is their relative relative speed.
- A boundary can be the boundary of an object centered on an internal object, or a channel such as a microphone, design or air channel that transmits a medium. Since Mach's number is defined as a two-speed ratio, it is an infinite number.
- If M <0.2-0.3 and the flow are not too volatile and visually impaired, the reduction results will be smaller and easier to measure the flow rate can be used.
Weber number
Weber (We) is a flawless number for liquid technologies that are often useful in analyzing fluid flow where there is a connection between two different liquids, especially multiphase flow with tightly curved surfaces. Named by Moritz Weber (1871–1951).
It can be considered as a measure of the relative importance of fluid inertia compared to groundwater. The quantity helps to test the small flow of the film and the formation of droplets and bubbles.
Euler number
In the statistics, the Euler numbers sequence En numbers (A122045 sequence in OEIS) described the extension of the Taylor series
1/ cosh t = 2 / et + e-t
Where cosh t is hyperbolic cosine. Euler numbers are associated with a specific number of Euler polynomials, namely:
E n = 2 n E n (1/ 2)
Euler's numbers come from the growing series of Taylor's secretive and hyperbolic secant activities. The latter is a function in the definition. They also appear in combinations, especially when calculating the number of exchange permissions for a set with a number of items.
Unit - 6
Unit - 6
Dimensional Analysis and Hydraulic Similitude
Q1) Explain Buckingham pi method?
A1)
- When a large number of physical variables are involved Rayleigh’s method of dimensional analysis becomes increasingly laborious and cumbersome.
- Buckingham’s method is an improvement over the Rayleigh’s method.
- Buckingham’s designated the dimensionless group by the letter Π. It is therefore often called Buckingham Π-Method.
- The Buckingham’s Π-Method states as follows:
“If there are n variables in a dimensionally homogeneous equation and if these variables contain fundamental dimensions (such as M, L, T, etc.) then the variables are arranged into (n-m) dimensionless terms.
- These dimensionless terms are called Π– terms.”
Mathematically, if any variable X1, depends on independent variables, X2, X3, X4,…… Xn; the functional equation may be written as
 -------- 1
-------- 1
Equation 1 can also be written as
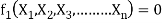 -------- 2
-------- 2
It is dimensionally homogeneous equation and contains n variables.
If there are m fundamental dimensions, then according to Buckingham’s Π – theorem, it [equation] can be written in terms of number of Π – terms in which number of Π terms is equal to (n-m).
Hence equation 2 becomes as
 --------3
--------3
Each dimensionless 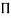 – term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
– term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
These m variables which appear repeated in each of  – terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
– terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
Let in the above case X2, X3 and X4 are the repeating variables if the fundamental dimensions m(M, L, T) = 3, then each term is written as:
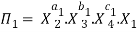
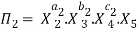
.
.
.
 -------- 4
-------- 4
Where a1, b1, c1, a2, b2, c2 etc. are the constants, which are determined by considering dimensional homogeneity. These values are substituted in equation 4 and values of  are obtained. These values of Π’s are substituted in equation 3.
are obtained. These values of Π’s are substituted in equation 3.
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:
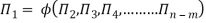
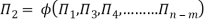
Q2) Explain the term Reynold Number.
A2)
Reynolds number
- Reynolds (Re) number helps to predict flow patterns in various fluid flow conditions. In low Reynolds numbers, the flow is usually dominated by laminar (sheet-like) flow, while at high Reynolds numbers the flow is often chaotic.
- Confusion is caused by variations in the speed of the curve and direction, which can sometimes combine or incite opposition to the full flow direction (eddy currents). These eddy currents begin to compress the flow, applying energy to the process, which in turn increases the chances of explosion. Reynolds numbers are immeasurably important for liquid mechanics.
- Reynolds number has a wide range of applications, ranging from the liquid flow of the pipe to the air flow over the wing of the aircraft. It is used to predict the transition from laminar to turbulent travel, and is used to measure the same flow conditions but with different sizes, such as between aircraft model in the air tunnel and a full-size version.
- Early predictor of turbulence and the ability to calculate the measurement results can be used to help predict liquid performance at a larger scale, such as in air and ground or water movement and thus to have climate-related and climate-related results.
- Reynolds number is a measure of the weak energy and viscous energy within a fluid that affects the corresponding internal movements due to the different velocities of the fluid. The region in which this force changes function is known as the boundary membrane, as the surface is enclosed within a pipe.
- The same effect is achieved by introducing high-velocity fluid currents into low-velocity fluid, like hot gases emitted by flames in the air. The movement associated with this creates a liquid tension, which is a factor in promoting turbulent flow.
- The opposite of this effect is the viscosity of the fluid, which usually prevents turbulence. Reynolds' number measures the relative importance of these two types of energy in the given flow conditions, and is an indication of when the turbulent flow will occur in a given situation.
- This ability to predict the onset of flow flows is an important invention of mechanical devices such as plumbing or wing systems, but Reynolds' number is also used to measure dynamic water problems, and is used to determine the dynamic similarity between two different fluids, such as between a model aircraft, and its full version.
- Such measurements are not online and the use of Reynolds numbers in both cases allows for enhanced rating features.
With respect to laminar and turbulent flow regimes:
- Laminar flow occurs with low Reynolds numbers, in which viscous forces are prominent, and are characterized by smooth, consistent movements;
- Turbulent flow occurs at high Reynolds numbers and is dominated by weak forces, often producing eddy, turbulence and other flow conflicts.
Reynolds' number is described as
Re = u L / 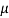
Where:
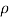 is the humidity (SI units: kg / m3)
is the humidity (SI units: kg / m3)
u is flow speed (m / s)
L different line size (m) (see paragraphs below this article for examples)
μ is the strong viscosity of the fluid (Pa · s or N · s / m2 or kg / (m · s))
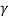 is the kinematic viscosity of fluid (m2 / s).
is the kinematic viscosity of fluid (m2 / s).
- Reynolds' number can be defined in a variety of situations where the fluid is a facial-related movement.
- These definitions usually include liquid properties of mass and viscosity, as well as the velocity and length of the element or the size of the element (L in the above figure). This size is a matter for the meeting - for example radius and scope work equally well to define sections or circles, but one is chosen by the meeting. On planes or ships, length or width can be used.
- The flow of the pipe, or liquid-moving phase, the internal diameter is widely used today. Other shapes such as rectangular pipes or non-circular objects have the same specified width. For liquefaction fluids such as compressed gases or fluid viscosity fluids such as non-Newtonia fluids, special rules apply. Speed can also be a matter of assembly in some cases, especially for renewable vessels.
- In practice, matching Reynolds' number is not enough in itself to ensure consistency. The flow of fluid is usually chaotic, and very small changes in the shape and appearance of the surface of the conjunctiva can lead to very different flow. However, Reynolds numbers are a very important guide and are widely used.
Q3) An oil of specific gravity 0.9 and viscosity 0.9 poise is to be transported at the rate of 1000 l/s through a. 1.2 m diameter pipe. Tests were conducted on a 10 cm diameter pipe using water at .20°C. Viscosity of water at 20°C is 0.01 poise. Find the rate of flow in the model.
A3)
Prototype
D = 1.2 m.
Sp = 0.9,
Model
Dm = 10 cm = 0.1 m
Sm = 1
μp = 0.9 poise. μm = 0.01 poise = 1 x 10-² poise
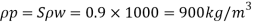
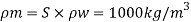
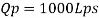
To find: Velocity and flow rate.
Since it is pipe flow, Reynolds’s number must be applied.
(Re)model = (R) prototype
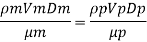


Rate of flow through model
Q4) From the following data, find the scale ratio of model Velocity of water 1 m/'s through circular pipe. Prototype: Velocity of oil 0.12 ms through 50 mm diameter pipe. Assume kinematic viscosity of water 0.01 cms and that of oil 0.008 cm/s. Assume dynamic similarity. Also find the diameter of pipe used for model.
A4)
Prototype
Vp -012 m/s
Dp = 50mm = 0.05 m
Vp = 0.006 cm²/sec
Model
Vm= 1m/s
Dm=?
Vm= 0.01 cm^2/sec
To find:
Since it is pipe flow, Reynold's ember mast be applied

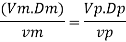
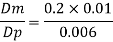
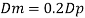
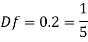
Model scale ratio is 1:5
Now, diameter of model pipe
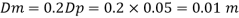
Q5) Water at 15.6°C flows at 3.5 m/s in a 150 mm diameter pipe. At what velocity must a fuel oil at 32.6°C flow in a 75 mm diameter pipe for the flow to be dynamic similar? v.-1.13 x 10 m/s and 2.96 x 10 m/s.
A5)
Water
Dw = 150 mm = 0.15 m

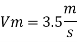
Oil
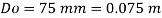

To find: Velocity of oil V.
Since it is pipe flow, Reynold's number must be applied

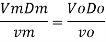
The velocity of cl at 32.6°C is 15.33 m'k
Q6) A ship has a length of 150 m and wetted area 3000 m² A model of this ship 5 m in length when towed in fresh water (p= 1000 kg/m) at 2 m/s produces a resistance of 40N. Calculate (1) corresponding speed of the ship. (i) the shaft power required to propel the ship at this speed through sea water (p=1030 kg/m). Take the propeller efficiency as 75%
A6)
Model
Lm= 5 m
Vm= 2 m/s
Fm = 40 N
Prototype
Lp= 150 m

Ap= 3000m^2
Propeller efficiency= n= 75 %
To find:
Speed of ship Vp
Since it is ship motion Reynolds number must be applied
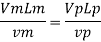
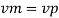
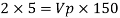
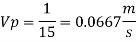
Ratio of drag force
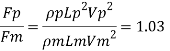
Drag force on prototype
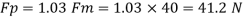

Actual power input
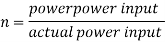
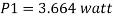
Q7) A ship 300 m long moves in seawater whose density is 1030 kg/m A1.75 Model of this ship is to be tested in a wind tunnel. The velocity of air in wind tunnel is 29 m/s the resistance of the model is 60 N. Determine velocity and resistance of the ship in seawater. Air density is 1.24 kg/m Kinematic viscosity of air=0.018 stokes Kinematic viscosity of seawater 0,01 stokes.
A7)
Given:
Prototype
Scale 1:75
Lp = 300 m
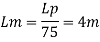
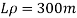


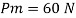
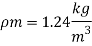
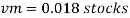

To find:
Vp and Fp
Since it is ship motion Reynolds number must be applied

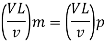
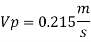
Drag force ratio
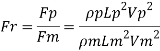
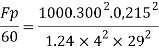

Q8) In a geometrically similar model of weir the discharge is 0.15 m².s.. if the scale of the model is 1/50 find the discharge of the prototype.
A8)
Given:
Discharge per meter length = 0.15 m/sec.
Scale ratio Lr = Lp/Lm = 50
To find: qp
Since it is a spillway, Froude Number must be applicable.
The discharge ratio for spillway is given by

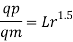
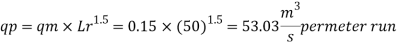
Q9) The performance of a spillway is to be studied by means of a model constructed to a scale of 1:9. Determine: (1) Rate of flow in the model for a prototype discharge of 1400 m/s. (2) Energy lost in the prototype if the energy loss in model is 0.3 kW
A9)
Given:
Scale of model 1:9
Lr = 9
Discharge of proto type Q = 1400 m^3 /s
Since it is a spillway, Froude number must be applicable.
Using discharge scale ratio
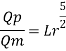
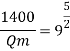
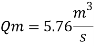
Energy loss
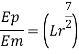
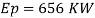
Q10) In the model test of a spillway the discharge per meter length is 1/6 m^3/sec if the scale of the model is 1/36 find the discharge per meter run of the prototype.
A10) Given:
Qm = 1/6 m^3/sec
Lr = Lp/Lm = 36
To find: QP
Since it is a spillway, Froude Number must be applicable. The discharge ratio for spillway is given by
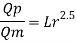
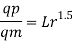

Q11) Find the suitable scale for model of a spillway if maximum discharge available in the laboratory is 10 L.P.S. And the prototype discharge is 168.07 m/sec.
A11)
Given:
Q=10 lps = 10 x10³ m³/sec;
Qp = 168.07 m^3/sec
Since it is a spillway, Froude Number must be applicable. Using discharge scale ratio

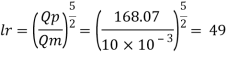
Model scale should be 1:49.
Q12) A ship model of scale 1/60 is towed through sea water at a speed of 1:1 m/s A force of 2.1 N is required to tow the model. Determine the speed of ship and the propulsive force on the ship if the prototype is subjected to wave resistance only.
A12)
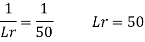
Speed of model Vm=1.1 m/s
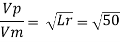
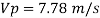
Resistance to prototype in sea water
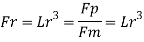
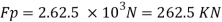
Q13) Explain the terms:
- Froude number
- Mach number
- Weber number
- Euler number
A13)
Froude number
Froude’s number, Fr, is an infinite number that describes the various states of open channel flow. Froude's number is a measure of gravity and gravity.
Gravity (number) - moves water down
Inertia (denominator) - shows its willingness to do so.
Fr = v / √ (g D)
Where:
V = Water speed
D = Hydraulic depth (flow area / over width)
g = Gravity
When:
Fr = 1, critical flow
Fr> 1, basic flow (fast flow)
Fr <1, poor flow (slow / silent)
- Froude's number is the measure of the flow signals such as waves, sand formation, flow / depth of contact in the cross section or between large rocks.
- The denominator represents the slower wave surface on the surface of water compared to the speed of the water, called wave celerity. In the flow of critical flow is similar to the flow of speed. Any facial distortion will remain standing. In a continuous flow the flow is controlled from below and the information is transmitted above. This condition leads to post-water effects. Excellent flow is controlled upwards and disturbances are transmitted downstream.
- Wave propagation can be used to illustrate these flow conditions: A stick placed in water will form a V-wave pattern below. If the flow is small waves will appear in front of the rod. If the flow is a critical wave it will have a 45o angle. If the flow is excessive the rising waves will appear and the wave angle will be below 45°.
Mach number
Mach (M or Ma) number is an infinite magnitude in the force of a liquid that represents the rate of flow rate beyond the local speed limit.
M = u / c
Where: M local Mack number,
u is the local velocity flow in relation to boundaries (either internal, such as something flow-focused, or external, as a channel), and
c is the speed of the sound in the middle, in the air which varies with the square root of the thermodynamic temperature.
- By definition, in March 1, the local flow speed is equal to the speed of the sound. In March 0.65, 65% is subsonic speed, and, on March 1.35, 35% is faster than supersonic speed.
- Pilots who use high-performance aircraft use the aircraft number to indicate the actual air conditioning of the vehicle, but the flow path around the vehicle varies in size by three, depending on the local area number.
- The local speed of the noise, which is why Mach's number also depends on the temperature of the surrounding gas. Mach number is used primarily to determine the limitations at which the flow can be treated as an inconsistent flow.
- The contents can be gas or liquid. The boundary can move in the middle, or it can be set while the center is flowing, or they can both go, at different speeds: what matters is their relative relative speed.
- A boundary can be the boundary of an object centered on an internal object, or a channel such as a microphone, design or air channel that transmits a medium. Since Mach's number is defined as a two-speed ratio, it is an infinite number.
- If M <0.2-0.3 and the flow are not too volatile and visually impaired, the reduction results will be smaller and easier to measure the flow rate can be used.
Weber number
Weber (We) is a flawless number for liquid technologies that are often useful in analyzing fluid flow where there is a connection between two different liquids, especially multiphase flow with tightly curved surfaces. Named by Moritz Weber (1871–1951).
It can be considered as a measure of the relative importance of fluid inertia compared to groundwater. The quantity helps to test the small flow of the film and the formation of droplets and bubbles.
Euler number
In the statistics, the Euler numbers sequence En numbers (A122045 sequence in OEIS) described the extension of the Taylor series
1/ cosh t = 2 / et + e-t
Where cosh t is hyperbolic cosine. Euler numbers are associated with a specific number of Euler polynomials, namely:
E n = 2 n E n (1/ 2)
Euler's numbers come from the growing series of Taylor's secretive and hyperbolic secant activities. The latter is a function in the definition. They also appear in combinations, especially when calculating the number of exchange permissions for a set with a number of items.
Unit - 6
Unit - 6
Dimensional Analysis and Hydraulic Similitude
Q1) Explain Buckingham pi method?
A1)
- When a large number of physical variables are involved Rayleigh’s method of dimensional analysis becomes increasingly laborious and cumbersome.
- Buckingham’s method is an improvement over the Rayleigh’s method.
- Buckingham’s designated the dimensionless group by the letter Π. It is therefore often called Buckingham Π-Method.
- The Buckingham’s Π-Method states as follows:
“If there are n variables in a dimensionally homogeneous equation and if these variables contain fundamental dimensions (such as M, L, T, etc.) then the variables are arranged into (n-m) dimensionless terms.
- These dimensionless terms are called Π– terms.”
Mathematically, if any variable X1, depends on independent variables, X2, X3, X4,…… Xn; the functional equation may be written as
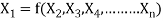 -------- 1
-------- 1
Equation 1 can also be written as
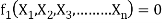 -------- 2
-------- 2
It is dimensionally homogeneous equation and contains n variables.
If there are m fundamental dimensions, then according to Buckingham’s Π – theorem, it [equation] can be written in terms of number of Π – terms in which number of Π terms is equal to (n-m).
Hence equation 2 becomes as
 --------3
--------3
Each dimensionless 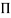 – term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
– term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
These m variables which appear repeated in each of 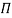 – terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
– terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimentions and they themselves do not form a dimensionless parameter.
Let in the above case X2, X3 and X4 are the repeating variables if the fundamental dimensions m(M, L, T) = 3, then each term is written as:


.
.
.
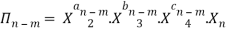 -------- 4
-------- 4
Where a1, b1, c1, a2, b2, c2 etc. are the constants, which are determined by considering dimensional homogeneity. These values are substituted in equation 4 and values of  are obtained. These values of Π’s are substituted in equation 3.
are obtained. These values of Π’s are substituted in equation 3.
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:


Q2) Explain the term Reynold Number.
A2)
Reynolds number
- Reynolds (Re) number helps to predict flow patterns in various fluid flow conditions. In low Reynolds numbers, the flow is usually dominated by laminar (sheet-like) flow, while at high Reynolds numbers the flow is often chaotic.
- Confusion is caused by variations in the speed of the curve and direction, which can sometimes combine or incite opposition to the full flow direction (eddy currents). These eddy currents begin to compress the flow, applying energy to the process, which in turn increases the chances of explosion. Reynolds numbers are immeasurably important for liquid mechanics.
- Reynolds number has a wide range of applications, ranging from the liquid flow of the pipe to the air flow over the wing of the aircraft. It is used to predict the transition from laminar to turbulent travel, and is used to measure the same flow conditions but with different sizes, such as between aircraft model in the air tunnel and a full-size version.
- Early predictor of turbulence and the ability to calculate the measurement results can be used to help predict liquid performance at a larger scale, such as in air and ground or water movement and thus to have climate-related and climate-related results.
- Reynolds number is a measure of the weak energy and viscous energy within a fluid that affects the corresponding internal movements due to the different velocities of the fluid. The region in which this force changes function is known as the boundary membrane, as the surface is enclosed within a pipe.
- The same effect is achieved by introducing high-velocity fluid currents into low-velocity fluid, like hot gases emitted by flames in the air. The movement associated with this creates a liquid tension, which is a factor in promoting turbulent flow.
- The opposite of this effect is the viscosity of the fluid, which usually prevents turbulence. Reynolds' number measures the relative importance of these two types of energy in the given flow conditions, and is an indication of when the turbulent flow will occur in a given situation.
- This ability to predict the onset of flow flows is an important invention of mechanical devices such as plumbing or wing systems, but Reynolds' number is also used to measure dynamic water problems, and is used to determine the dynamic similarity between two different fluids, such as between a model aircraft, and its full version.
- Such measurements are not online and the use of Reynolds numbers in both cases allows for enhanced rating features.
With respect to laminar and turbulent flow regimes:
- Laminar flow occurs with low Reynolds numbers, in which viscous forces are prominent, and are characterized by smooth, consistent movements;
- Turbulent flow occurs at high Reynolds numbers and is dominated by weak forces, often producing eddy, turbulence and other flow conflicts.
Reynolds' number is described as
Re = u L / 
Where:
 is the humidity (SI units: kg / m3)
is the humidity (SI units: kg / m3)
u is flow speed (m / s)
L different line size (m) (see paragraphs below this article for examples)
μ is the strong viscosity of the fluid (Pa · s or N · s / m2 or kg / (m · s))
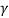 is the kinematic viscosity of fluid (m2 / s).
is the kinematic viscosity of fluid (m2 / s).
- Reynolds' number can be defined in a variety of situations where the fluid is a facial-related movement.
- These definitions usually include liquid properties of mass and viscosity, as well as the velocity and length of the element or the size of the element (L in the above figure). This size is a matter for the meeting - for example radius and scope work equally well to define sections or circles, but one is chosen by the meeting. On planes or ships, length or width can be used.
- The flow of the pipe, or liquid-moving phase, the internal diameter is widely used today. Other shapes such as rectangular pipes or non-circular objects have the same specified width. For liquefaction fluids such as compressed gases or fluid viscosity fluids such as non-Newtonia fluids, special rules apply. Speed can also be a matter of assembly in some cases, especially for renewable vessels.
- In practice, matching Reynolds' number is not enough in itself to ensure consistency. The flow of fluid is usually chaotic, and very small changes in the shape and appearance of the surface of the conjunctiva can lead to very different flow. However, Reynolds numbers are a very important guide and are widely used.
Q3) An oil of specific gravity 0.9 and viscosity 0.9 poise is to be transported at the rate of 1000 l/s through a. 1.2 m diameter pipe. Tests were conducted on a 10 cm diameter pipe using water at .20°C. Viscosity of water at 20°C is 0.01 poise. Find the rate of flow in the model.
A3)
Prototype
D = 1.2 m.
Sp = 0.9,
Model
Dm = 10 cm = 0.1 m
Sm = 1
μp = 0.9 poise. μm = 0.01 poise = 1 x 10-² poise

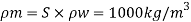

To find: Velocity and flow rate.
Since it is pipe flow, Reynolds’s number must be applied.
(Re)model = (R) prototype
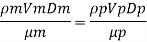
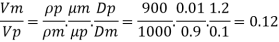
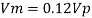
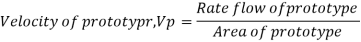
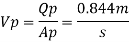
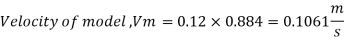
Rate of flow through model
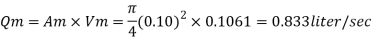
Q4) From the following data, find the scale ratio of model Velocity of water 1 m/'s through circular pipe. Prototype: Velocity of oil 0.12 ms through 50 mm diameter pipe. Assume kinematic viscosity of water 0.01 cms and that of oil 0.008 cm/s. Assume dynamic similarity. Also find the diameter of pipe used for model.
A4)
Prototype
Vp -012 m/s
Dp = 50mm = 0.05 m
Vp = 0.006 cm²/sec
Model
Vm= 1m/s
Dm=?
Vm= 0.01 cm^2/sec
To find:
Since it is pipe flow, Reynold's ember mast be applied

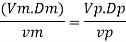
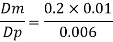
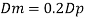

Model scale ratio is 1:5
Now, diameter of model pipe
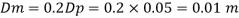
Q5) Water at 15.6°C flows at 3.5 m/s in a 150 mm diameter pipe. At what velocity must a fuel oil at 32.6°C flow in a 75 mm diameter pipe for the flow to be dynamic similar? v.-1.13 x 10 m/s and 2.96 x 10 m/s.
A5)
Water
Dw = 150 mm = 0.15 m
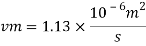

Oil
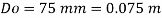

To find: Velocity of oil V.
Since it is pipe flow, Reynold's number must be applied
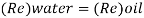
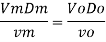
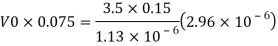
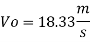
The velocity of cl at 32.6°C is 15.33 m'k
Q6) A ship has a length of 150 m and wetted area 3000 m² A model of this ship 5 m in length when towed in fresh water (p= 1000 kg/m) at 2 m/s produces a resistance of 40N. Calculate (1) corresponding speed of the ship. (i) the shaft power required to propel the ship at this speed through sea water (p=1030 kg/m). Take the propeller efficiency as 75%
A6)
Model
Lm= 5 m

Vm= 2 m/s
Fm = 40 N
Prototype
Lp= 150 m
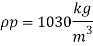
Ap= 3000m^2
Propeller efficiency= n= 75 %
To find:
Speed of ship Vp
Since it is ship motion Reynolds number must be applied
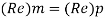
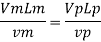

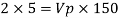
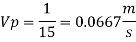
Ratio of drag force
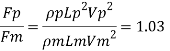
Drag force on prototype
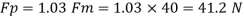

Actual power input

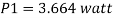
Q7) A ship 300 m long moves in seawater whose density is 1030 kg/m A1.75 Model of this ship is to be tested in a wind tunnel. The velocity of air in wind tunnel is 29 m/s the resistance of the model is 60 N. Determine velocity and resistance of the ship in seawater. Air density is 1.24 kg/m Kinematic viscosity of air=0.018 stokes Kinematic viscosity of seawater 0,01 stokes.
A7)
Given:
Prototype
Scale 1:75
Lp = 300 m
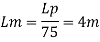
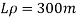
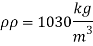
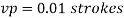
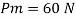
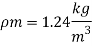
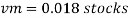
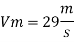
To find:
Vp and Fp
Since it is ship motion Reynolds number must be applied
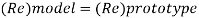

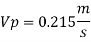
Drag force ratio

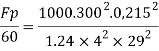
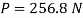
Q8) In a geometrically similar model of weir the discharge is 0.15 m².s.. if the scale of the model is 1/50 find the discharge of the prototype.
A8)
Given:
Discharge per meter length = 0.15 m/sec.
Scale ratio Lr = Lp/Lm = 50
To find: qp
Since it is a spillway, Froude Number must be applicable.
The discharge ratio for spillway is given by
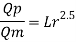
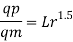

Q9) The performance of a spillway is to be studied by means of a model constructed to a scale of 1:9. Determine: (1) Rate of flow in the model for a prototype discharge of 1400 m/s. (2) Energy lost in the prototype if the energy loss in model is 0.3 kW
A9)
Given:
Scale of model 1:9
Lr = 9
Discharge of proto type Q = 1400 m^3 /s
Since it is a spillway, Froude number must be applicable.
Using discharge scale ratio
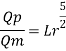

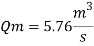
Energy loss

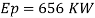
Q10) In the model test of a spillway the discharge per meter length is 1/6 m^3/sec if the scale of the model is 1/36 find the discharge per meter run of the prototype.
A10) Given:
Qm = 1/6 m^3/sec
Lr = Lp/Lm = 36
To find: QP
Since it is a spillway, Froude Number must be applicable. The discharge ratio for spillway is given by

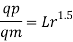
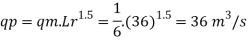
Q11) Find the suitable scale for model of a spillway if maximum discharge available in the laboratory is 10 L.P.S. And the prototype discharge is 168.07 m/sec.
A11)
Given:
Q=10 lps = 10 x10³ m³/sec;
Qp = 168.07 m^3/sec
Since it is a spillway, Froude Number must be applicable. Using discharge scale ratio
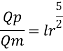

Model scale should be 1:49.
Q12) A ship model of scale 1/60 is towed through sea water at a speed of 1:1 m/s A force of 2.1 N is required to tow the model. Determine the speed of ship and the propulsive force on the ship if the prototype is subjected to wave resistance only.
A12)
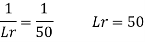
Speed of model Vm=1.1 m/s


Resistance to prototype in sea water
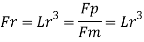
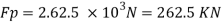
Q13) Explain the terms:
- Froude number
- Mach number
- Weber number
- Euler number
A13)
Froude number
Froude’s number, Fr, is an infinite number that describes the various states of open channel flow. Froude's number is a measure of gravity and gravity.
Gravity (number) - moves water down
Inertia (denominator) - shows its willingness to do so.
Fr = v / √ (g D)
Where:
V = Water speed
D = Hydraulic depth (flow area / over width)
g = Gravity
When:
Fr = 1, critical flow
Fr> 1, basic flow (fast flow)
Fr <1, poor flow (slow / silent)
- Froude's number is the measure of the flow signals such as waves, sand formation, flow / depth of contact in the cross section or between large rocks.
- The denominator represents the slower wave surface on the surface of water compared to the speed of the water, called wave celerity. In the flow of critical flow is similar to the flow of speed. Any facial distortion will remain standing. In a continuous flow the flow is controlled from below and the information is transmitted above. This condition leads to post-water effects. Excellent flow is controlled upwards and disturbances are transmitted downstream.
- Wave propagation can be used to illustrate these flow conditions: A stick placed in water will form a V-wave pattern below. If the flow is small waves will appear in front of the rod. If the flow is a critical wave it will have a 45o angle. If the flow is excessive the rising waves will appear and the wave angle will be below 45°.
Mach number
Mach (M or Ma) number is an infinite magnitude in the force of a liquid that represents the rate of flow rate beyond the local speed limit.
M = u / c
Where: M local Mack number,
u is the local velocity flow in relation to boundaries (either internal, such as something flow-focused, or external, as a channel), and
c is the speed of the sound in the middle, in the air which varies with the square root of the thermodynamic temperature.
- By definition, in March 1, the local flow speed is equal to the speed of the sound. In March 0.65, 65% is subsonic speed, and, on March 1.35, 35% is faster than supersonic speed.
- Pilots who use high-performance aircraft use the aircraft number to indicate the actual air conditioning of the vehicle, but the flow path around the vehicle varies in size by three, depending on the local area number.
- The local speed of the noise, which is why Mach's number also depends on the temperature of the surrounding gas. Mach number is used primarily to determine the limitations at which the flow can be treated as an inconsistent flow.
- The contents can be gas or liquid. The boundary can move in the middle, or it can be set while the center is flowing, or they can both go, at different speeds: what matters is their relative relative speed.
- A boundary can be the boundary of an object centered on an internal object, or a channel such as a microphone, design or air channel that transmits a medium. Since Mach's number is defined as a two-speed ratio, it is an infinite number.
- If M <0.2-0.3 and the flow are not too volatile and visually impaired, the reduction results will be smaller and easier to measure the flow rate can be used.
Weber number
Weber (We) is a flawless number for liquid technologies that are often useful in analyzing fluid flow where there is a connection between two different liquids, especially multiphase flow with tightly curved surfaces. Named by Moritz Weber (1871–1951).
It can be considered as a measure of the relative importance of fluid inertia compared to groundwater. The quantity helps to test the small flow of the film and the formation of droplets and bubbles.
Euler number
In the statistics, the Euler numbers sequence En numbers (A122045 sequence in OEIS) described the extension of the Taylor series
1/ cosh t = 2 / et + e-t
Where cosh t is hyperbolic cosine. Euler numbers are associated with a specific number of Euler polynomials, namely:
E n = 2 n E n (1/ 2)
Euler's numbers come from the growing series of Taylor's secretive and hyperbolic secant activities. The latter is a function in the definition. They also appear in combinations, especially when calculating the number of exchange permissions for a set with a number of items.