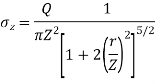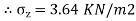Unit - 2

Stress Distribution in Soils

Q1) What is Stress distribution?

A1)

• Stresses in soil is caused by the self-weight of soil and /or structural loads, applied at or below the surface.
• The study of stress distribution in soils have many applications to field problems where transmission and distribution of stresses is in large and extensive masses of soil. [e.g., transmission of wheel loads through embankments to culverts, pressure of foundation to soil strata below footings, pressures from isolated footings transmitted to retaining walls and transmission of wheel loads through stabilized soil pavements to sub-grades below.] This study is useful to the prediction of settlements of buildings, bridges and embankments.

Q2) What are the normal and shear stresses on plane?

A2)

• There are two principal stresses like major and minor principal stresses are to be considered and third principal stress in the third direction is not much relevance. Major principal stress (): The normal stress without shear stress acting on the major principal plane is called as major principal stress ().
• Minor principal stress (): the normal stress without shear stress acting on the minor principal plane is called as minor principal stress ().
• The intermediate principal stress () is not much: relevant, hence not considered in the many problems in geotechnical engineering, only major principal stress (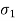) and minor principal stress (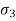) are important.
• Following equation shows the equation of circle,

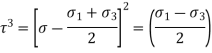
Normal stress

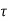= shear stress

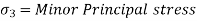
The co-ordinates of centre of circle are 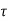= 0 and

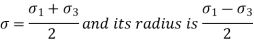
Stress Distribution on horizontal and vertical planes:

Pressure distribution diagram on horizontal plane:

• Consider a horizontal plane at a depth Z from point of application of load Q
• Hence the vertical stress on horizontal plane due to point load acting at surface is

=

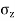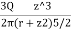
Where 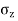=Vertical stress on horizontal plane

Z=Depth from the point of application of load

r=horizontal distance of a point from a point load

Q = point load

Pressure Distribution Diagram on a Vertical Plane:

• Consider a vertical plane at radial distance r from a point load acting on the surface of soil mass, The equation is useful to calculate stress on a vertical plane.

e.g., Let Q= 150 KN and r=3m

=

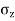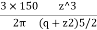
Following table gives the values of a, for different depths.

Z(m)	(KN/m2)
1m	0.295
2m	0.94
3m	1.407
4m	1.467
5m	1.328
6m	1.1388

Q3) Explain Boussinesque’s Theory?

A3)

The problem of stress evaluation at a point inside soil mass due to point load acting on the surface of a homogeneous, elastic, isotropic and semi-infinite medium of soil mass has solved by BoussinesQ

Assumptions Made by Boussinesq:

1. The soil medium is an elastic, homogeneous, isotropic and semi-infinite medium.
2. The soil medium obeys Hooke's law.
3. The self-weight of the soil is ignored.
4. The soil is initially unstressed.
5. The change in soil volume due to load application is neglected.
6. The top surface of the soil is free of shear stress and only point load is acting at a point.

• Consider a point load Q acting at point O. Consider point 'S' inside soil mass where is acting.

Fig.: Vertical stress due to point load

=

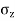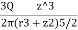
Where r= radial distance of point S from axis of load

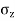= Vertical stress at point 'S'

R =Polar radial co-ordinate

The above Equation (iii) can be written as

= KB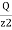    where, KB=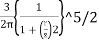

KB is Boussinesq's influence factor.

Shear stress at point S due to point load Q is,

Trz=^5/2

The typical values of KB are as follows:

Table: Values of influence factor for r/z ratios

Q4) Explain Boussinesq's Theory for Circular Load?

A4)

• Consider the loaded circular area of radius a, 'q' is uniformly distributed load intensity on circular area. Consider elemental ring of radius 'r' and thickness dr.

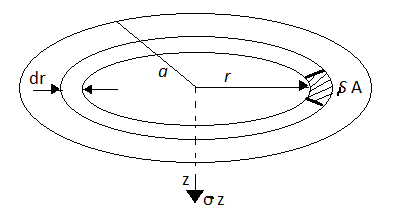
Fig.: Vertical stress on circular area

• Consider point 'P' at depth Z from the centre of loaded area.
• The vertical stress at a depth. 'Z' under the centre of circular area of diameter 'a' is,

=

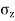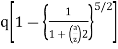
Q5) Explain Westergaard's Theory?

A5)

• Boussinesq's theory for determination of vertical stress in a soil mass is for isotropic soils. But if soil deposits like sedimentary deposits are generally made up of thin layers of sand and homogeneous clay strata (i.e. anisotropic).
• Westergaard's theory for solution of stresses is related to such soils only. This theory is more suitable for stratified soil layers (i.c. Sedimentary deposits).

Assumptions in Westergaard's theory:

1. The soil mass is an elastic medium.
2. The modulus of elasticity (E) of soil is constant.
3. The soil mass is semi-infinite in extent i.e. boundary surface is ground level itself but extends infinitely in all other directions.
4. The soil mass is anisotropic i.e. properties are not same throughout the soil mass.

The vertical stress from Fig.

Where,ɳ=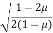             

The 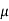value of 0.2 to 0.3 in above equation is quite realistic for many types of stratified soil deposits.In many cases,for practical purposes 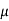is taken as zero.

=

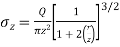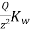
Where,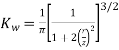

is called Westergard influence factor.

Table: Westergard Influence factor

Q6) What are the assumptions made by Boussinnesq?

A6)

Assumptions made by Boussinnesq are as follows:

1. The soil medium is an elastic, homogeneous, isotropic and semi-infinite medium.
2. The soil medium obeys Hooke's law.
3. The self weight of the soil is ignored.
4. The soil is initially unstressed.
5. The change in soil volume due to load application is neglected.
6. The top surface of the soil is free of shear stress and only point load is acting at a point.

Q7) What are the assumptions made by Westergaard’s theory?

A7)

1. The soil mass is an elastic medium.
2. The modulus of elasticity (E) of soil is constant.
3. The soil mass is semi-infinite in extent i.e. boundary surface is ground level itself but extends infinitely in all other directions.
4. The soil mass is anisotropic i.e. properties are not same throughout the soil mass.

Q8) What is Pressure bulb?

A8)

• Pressure bulb is also known as Isobar.
• 'Isobar' is a line or contour joining points of equal vertical stress inside soil mass.
• Isobar is a spatial curve which shows the same vertical pressure at all points in a horizontal plane at equal radial distances from the load. This stress isobar is bulb in shape hence it is called as pressure bulb. The area outside the pressure bulb is assumed to have negligible stresses. The zone within which the stresses have a significant effect on the settlement of structures is known as the pressure bulb.

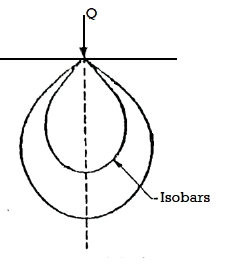
Fig.: Isobar

• The Boussinesq Equation for vertical stress due to point load is,

=

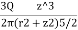
• Stress isobars for different vertical stress intensity can be plotted.

Q9) What is Newmark’s charts and their use?

A9)

• Newmark’s impact chart is used to decide the vertical strain underside of uniformly loaded bendy regions for any form of soil.
• This technique is derived from the Boussinesq’s equation for factor load through integration.

Construction and applications:

• Newmark’s impact chart is built through building a concentric circle. When the circles are similarly through drawing radially lines, which might be similarly spaced. The radius of the circle is R/z values.
• z is the intensity underneath to uniformly loaded location wherein growing pressure is obtained
• Today name duration of chart B, plot the pinnacle view our plan for the loaded location of the corresponding scale.
• Newmark’s impact chart location over the factor wherein the pressure is decided through finding the middle of the chart.
• Count the range of factors and the part of the chat enclosed through the plan of the loaded location.

Q10) A concentrated load of 40 KN is applied vertically on ground surface. Determine the vertical stress intensities at the following points:

1)At a depth of 3m below the point of application of the load.

2)At a depth of 1m and at a radial distance of 3m from the line of action of load.

A10)

1) Given: Z=3m,Q=40KN

Here r=0 due to stress intensity below the point of application of load.

To find stress intensity()

Using Boussinesq’s equation as,

=

=

∴

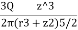
2)To find stress intensity at a depth of 1m and at a radial distance of 3m from the load

Here Z=depth=1m and r=radial distance=3m

Using Boussinesq’s equation as,

=

=

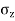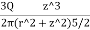
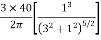
Q11) A concentrated load of 100 kN acts on the surface of homogenous soil mass of large extent. Find the stress intensity at a depth of 4 meters directly under the load. Use Bossinesq’s equation.

A11)

Given:

Q=100KN

Z=depth=4m

Since the stress intensity is directly under the load ,r=0

To find stress intensity (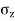) by Bossinesq’s equation,

=

=

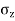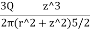
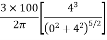
Q12) A concentrated load of 300KN is applied at the ground surface. Compute the vertical pressure.

1)at a depth of 6m below the load

2)at a distance of 5m at the same depth

A12)

Given:

Q=300KN, z=6m, r=5m

1. To compute the vertical pressure at a depth of 6m below the load:

Using Boussinesq’s equation as,

=

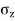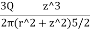
Since the stress intensity directly below the load,r=0

=

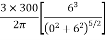
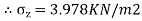
2.To compute vertical stress at a horizontal distance of 5m

Here z=6m, and r=5m

=

=

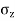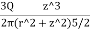
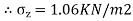
Q13) A load of 1000KN acts as a point load at the surface of a soil mass. Estimate the stress at appoint 3m below and 4m away from the point of action of the load by Bossinesq’s formula. Compare the value with the result from westergaard’s theory.

A13)

Given:

Q=load=1000KN

Z=3m, r=4m

1. As per Boussinesq’s theory

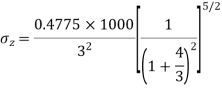
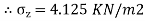
2. As per Westergaard theory: