Unit – 2
Reduction formula for integrals
Q1) What is the reduction formula for 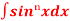 ?
?
A1)
Let, Iⁿ = 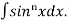 =
=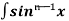 sinxdx , if n>1
sinxdx , if n>1
Taking 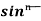 ¹x as first function and sinx as second function, integrate by parts,
¹x as first function and sinx as second function, integrate by parts,
Iⁿ = -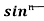 ¹x cosx – (n -1)
¹x cosx – (n -1) cosx(-cosx)dx
cosx(-cosx)dx
= -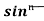 ¹x cosx + (n - 1)
¹x cosx + (n - 1)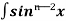 cos²xdx
cos²xdx
= -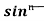 ¹x cosx + (n - 1)
¹x cosx + (n - 1) ( 1 - sin²x) dx
( 1 - sin²x) dx
= -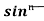 ¹x cosx + (n - 1)
¹x cosx + (n - 1)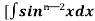 -
- 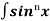 dx
dx
= -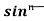 ¹x cosx + (n - 1) [ Iⁿ ‾ ² - Iⁿ]
¹x cosx + (n - 1) [ Iⁿ ‾ ² - Iⁿ]
By solving above
Iⁿ =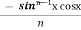 +
+ 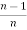 Iⁿ‾²
Iⁿ‾²
This is the reduction formula for 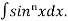
Q2) Evaluate  .
.
A2)
We will apply reduction formula to evaluate,
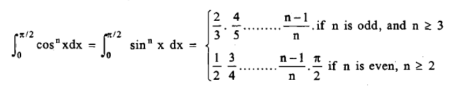
So, here n = 5, which is odd, we will get ,
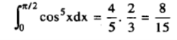
Q3) Evaluate 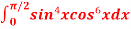 by using reduction formula.
by using reduction formula.
A3)
Here, m = 4, n = 6,
Now we will apply above reduction formula,
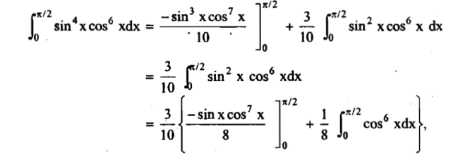
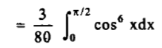
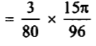
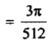
Q4) Give the reduction for 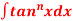 .
.
A4)
Let
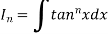
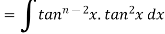
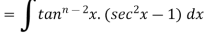
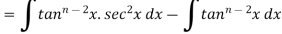
Thus, the required reduction formula is-
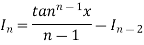
Q5) Evaluate  by using reduction formula.
by using reduction formula.
A5)
Put n = 6, 4, and 2 successively in the reduction formula for 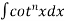 , we obtain-
, we obtain-
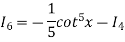
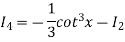
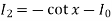
Thus
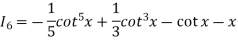
Q6) If 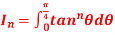 then prove that
then prove that 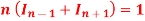
A6)
The reduction formula for 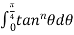 is-
is-
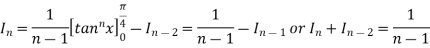
On changing n to n+1, we get-

Or
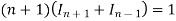
Hence proved
Q7) Give the properties of improper integrals.
A7)
Properties-
1. The definite integral applies only if a<b, but it would be appropriate to include the case a = b and a>b as well, in that case-
If a = b, then
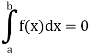
And if a>b, then
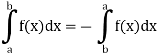
2. Integral of a constant function-
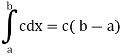
3. Constant multiple property-
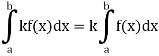
4. Interval union property-
If a < c < b, then
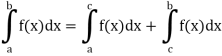
5. Inequality-
If c and d are constants such that 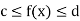 for all x in [a, b], then
for all x in [a, b], then
c (b – a)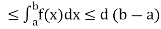
Note- if a function f: [a,b] →R is continuous, then the function ‘f’ is always Integrable.
Q8) Evaluate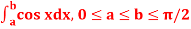 .
.
A8)
Here we notice that f:x→cos x is a decreasing function on [a, b],
Therefore, by the definition of the definite integrals-
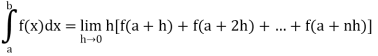
Then
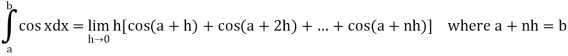
Now,
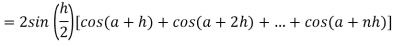
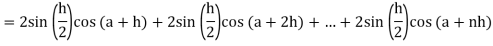

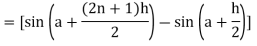
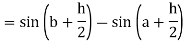
Here 
Thus
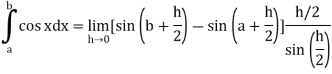
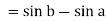
Q9) Evaluate 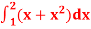
A9)
Here  is an increasing function on [1, 2]
is an increasing function on [1, 2]
So that,
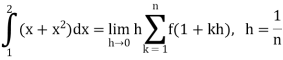
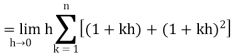
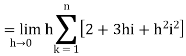
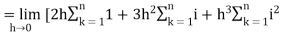 …. (1)
…. (1)
We know that-

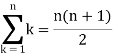
And 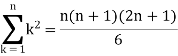
Then equation (1) becomes-

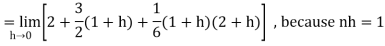
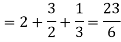
Q10) Evaluate-

A10)
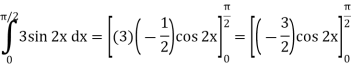
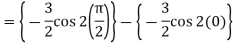
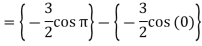
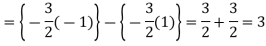
Q11) What do you understand by improper integrals over finite intervals?
A11)
(1) Let f is function defined on (a, b] and 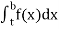 exists for all t ∈ (a,b), then
exists for all t ∈ (a,b), then
If 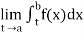 exists, then we define the improper integral of f over (a, b] as follows-
exists, then we define the improper integral of f over (a, b] as follows-
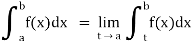
(2) Let f is function defined on [a, b) and  exists for all t ∈ (a,b), then
exists for all t ∈ (a,b), then
If 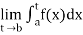 exists, then we define the improper integral of f over [a, b) as follows-
exists, then we define the improper integral of f over [a, b) as follows-
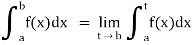
(3) Let f is function defined on [a, c) and (c, b]. If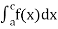 and
and 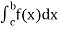 exist
exist
Then we define the improper integral of f over [a, b] as follows-
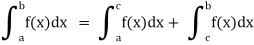
Q12) Evaluate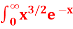 dx
dx
A12)
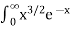 dx =
dx = 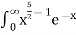 dx
dx
= Γ (5/2)
= Γ (3/2+ 1)
= 3/2 Γ (3/2)
= 3/2. ½ Γ (½)
= 3/2. ½ π
= ¾ π
Q13) Evaluate 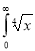
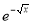 dx.
dx.
A13)
Let 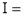
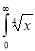
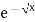 dx
dx
X | 0 | 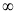 |
t | 0 | 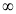 |
Put 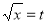 or
or 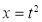 ;dx =2t dt
;dx =2t dt
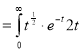 dt
dt
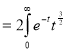 dt
dt
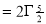


Q14) Evaluate I = 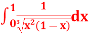
A14)
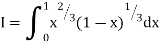
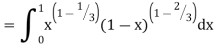
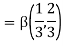
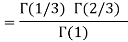
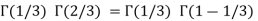
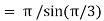
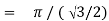
= 2 π/3
Q15) Prove that:
If 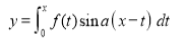 , then show that
, then show that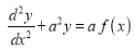 .
.
A15)
We have given that
 - - - - - - - - - - - - - - - - (1)
- - - - - - - - - - - - - - - - (1)
Then we have to prove that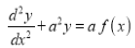 .
.
Differentiating by DUIS rule (Leibnitz’s Rule), we have
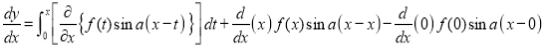
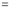
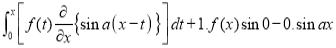
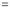
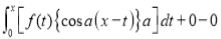
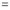
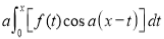
Again differentiating by DUIS rule (Leibnitz’s Rule), we have
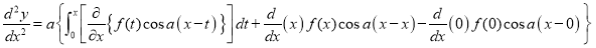
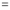
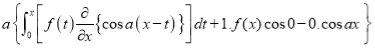
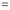
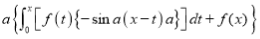

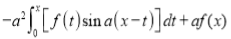
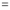
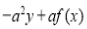
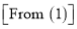
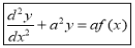
This is the desired result.
(ii)If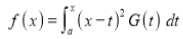 , then prove that
, then prove that .
.
We have given that
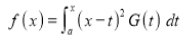 - - - - - - - - - - - - - - - - (1)
- - - - - - - - - - - - - - - - (1)
Then we have to prove that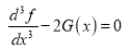 .
.
Differentiating by DUIS rule (Leibnitz’s Rule), we have
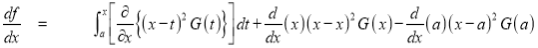
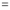

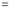
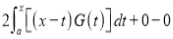
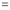
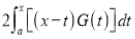
Again differentiating by DUIS rule (Leibnitz’s Rule), we have
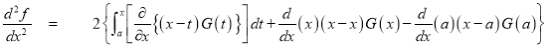
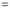
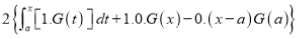
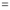

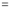
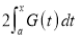
Again differentiating by DUIS rule (Leibnitz’s Rule), we have
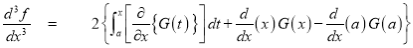
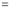

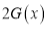

Q16) Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
A16)
Let,
y = 2 – x ………………..(1)
And y² = 2 (2 – x) ………………..(2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2) ,
We know that,
Area = 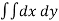
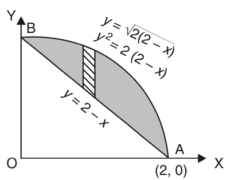
Here we will find the area as below,
Area = 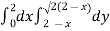
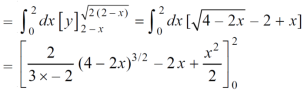
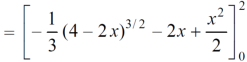
Which gives,
= ( - 4 + 4 /2 ) + 8 / 3 = 2 / 3.
Q17) Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.
A17)
We have,
r = a(1+cosθ) …………………….(1)
And
r = a ……………………………….(2)
On solving these equations by eliminating r , we get
a(1+cosθ) = a
(1+cosθ) = 1
Cosθ = 0
Here a θ varies from – π/2 to π/2
Limit of r will be a and 1+cosθ)
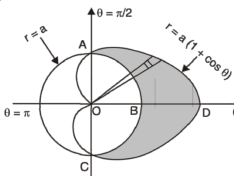
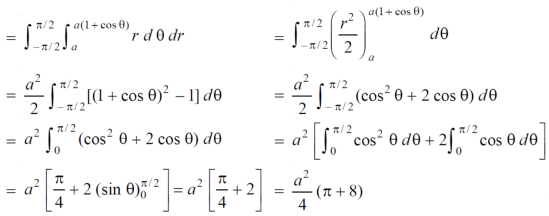
Which is the required area.
Q18) Calculate the volume generated by the revolution of a cardioid,
r = a ( 1 – cosθ) about its axis
A18)
Here, r = a ( 1 – cosθ)
Volume =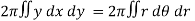
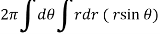
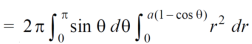
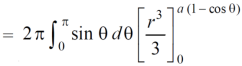
=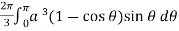
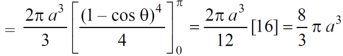
Which is the volume of generated by cardioid.
Q19) Find the area enclosed by the curves  and if the area is rotated
and if the area is rotated  about the x-axis then determine the volume of the solid of revolution.
about the x-axis then determine the volume of the solid of revolution.
A19)
We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-
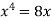
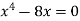
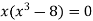
We get,
x = 0 and x = 2
The curve of the given equations will look like as follows-
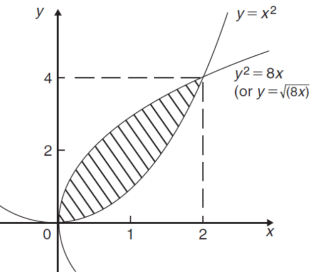
Then,
The area of the shaded region will be-
A = 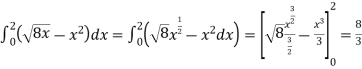
So that the area will be 8/3 square unit.
The volume will be
= (volume produced by revolving 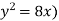 – (volume produced by revolving
– (volume produced by revolving 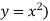
= 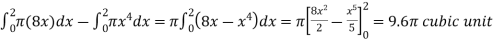
Q20) Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1 , 3].
A20)
The graph of the function f(x) = 1/x will look like-
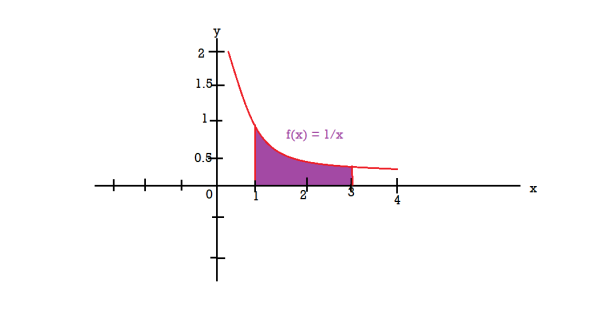
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]
Then the volume of the solid will be-
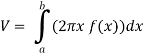
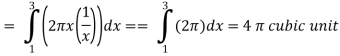
Q21) Find the mass of a plate formed by the coordinate planes and the plane-
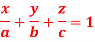
The variable density 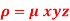
A21)
Here we the mass will be-
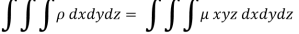
The limits of y are from y = 0 to y = b(1 – x/a) and limits of x are from 0 to a.
Therefore the required mass will be-
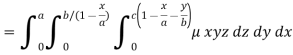
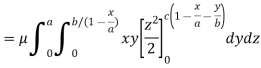
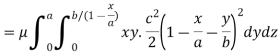
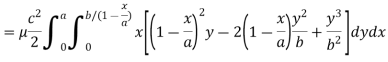
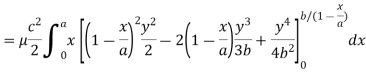
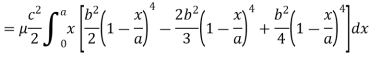
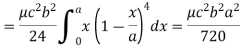
Which is the required answer.
Unit – 2
Reduction formula for integrals
Q1) What is the reduction formula for 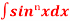 ?
?
A1)
Let, Iⁿ = 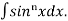 =
=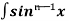 sinxdx , if n>1
sinxdx , if n>1
Taking 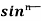 ¹x as first function and sinx as second function, integrate by parts,
¹x as first function and sinx as second function, integrate by parts,
Iⁿ = -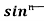 ¹x cosx – (n -1)
¹x cosx – (n -1)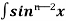 cosx(-cosx)dx
cosx(-cosx)dx
= -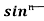 ¹x cosx + (n - 1)
¹x cosx + (n - 1)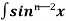 cos²xdx
cos²xdx
= -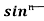 ¹x cosx + (n - 1)
¹x cosx + (n - 1)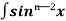 ( 1 - sin²x) dx
( 1 - sin²x) dx
= -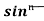 ¹x cosx + (n - 1)
¹x cosx + (n - 1)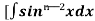 -
-  dx
dx
= -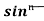 ¹x cosx + (n - 1) [ Iⁿ ‾ ² - Iⁿ]
¹x cosx + (n - 1) [ Iⁿ ‾ ² - Iⁿ]
By solving above
Iⁿ =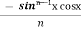 +
+  Iⁿ‾²
Iⁿ‾²
This is the reduction formula for 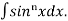
Q2) Evaluate  .
.
A2)
We will apply reduction formula to evaluate,
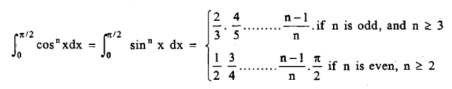
So, here n = 5, which is odd, we will get ,
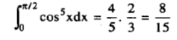
Q3) Evaluate 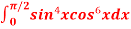 by using reduction formula.
by using reduction formula.
A3)
Here, m = 4, n = 6,
Now we will apply above reduction formula,
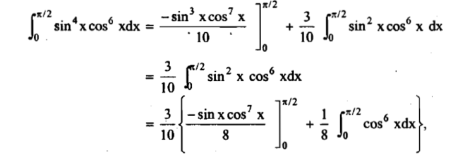

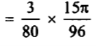

Q4) Give the reduction for 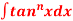 .
.
A4)
Let
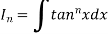
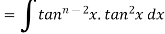
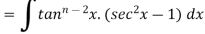
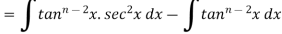
Thus, the required reduction formula is-
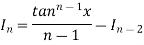
Q5) Evaluate 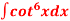 by using reduction formula.
by using reduction formula.
A5)
Put n = 6, 4, and 2 successively in the reduction formula for 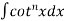 , we obtain-
, we obtain-
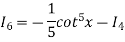
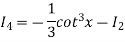
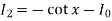
Thus
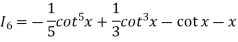
Q6) If 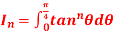 then prove that
then prove that 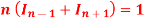
A6)
The reduction formula for 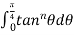 is-
is-
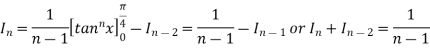
On changing n to n+1, we get-
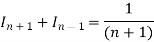
Or
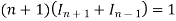
Hence proved
Q7) Give the properties of improper integrals.
A7)
Properties-
1. The definite integral applies only if a<b, but it would be appropriate to include the case a = b and a>b as well, in that case-
If a = b, then
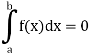
And if a>b, then
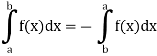
2. Integral of a constant function-
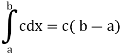
3. Constant multiple property-
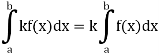
4. Interval union property-
If a < c < b, then

5. Inequality-
If c and d are constants such that 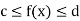 for all x in [a, b], then
for all x in [a, b], then
c (b – a)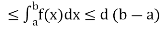
Note- if a function f: [a,b] →R is continuous, then the function ‘f’ is always Integrable.
Q8) Evaluate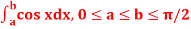 .
.
A8)
Here we notice that f:x→cos x is a decreasing function on [a, b],
Therefore, by the definition of the definite integrals-
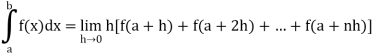
Then
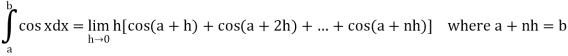
Now,
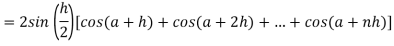
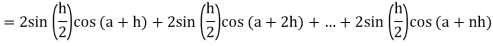

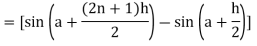
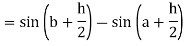
Here 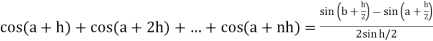
Thus
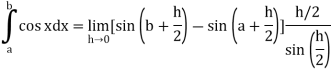
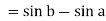
Q9) Evaluate 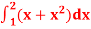
A9)
Here 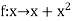 is an increasing function on [1, 2]
is an increasing function on [1, 2]
So that,
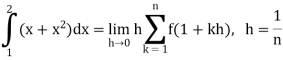
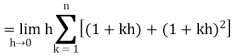
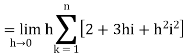
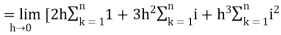 …. (1)
…. (1)
We know that-
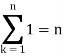
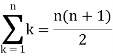
And 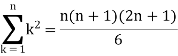
Then equation (1) becomes-
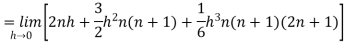
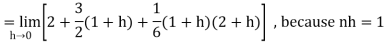
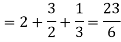
Q10) Evaluate-

A10)
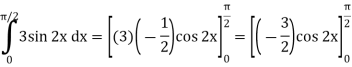
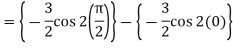
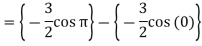
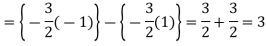
Q11) What do you understand by improper integrals over finite intervals?
A11)
(1) Let f is function defined on (a, b] and  exists for all t ∈ (a,b), then
exists for all t ∈ (a,b), then
If 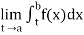 exists, then we define the improper integral of f over (a, b] as follows-
exists, then we define the improper integral of f over (a, b] as follows-
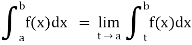
(2) Let f is function defined on [a, b) and 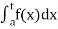 exists for all t ∈ (a,b), then
exists for all t ∈ (a,b), then
If 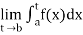 exists, then we define the improper integral of f over [a, b) as follows-
exists, then we define the improper integral of f over [a, b) as follows-
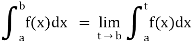
(3) Let f is function defined on [a, c) and (c, b]. If and
and 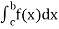 exist
exist
Then we define the improper integral of f over [a, b] as follows-
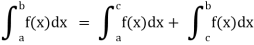
Q12) Evaluate dx
dx
A12)
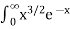 dx =
dx = 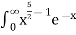 dx
dx
= Γ (5/2)
= Γ (3/2+ 1)
= 3/2 Γ (3/2)
= 3/2. ½ Γ (½)
= 3/2. ½ π
= ¾ π
Q13) Evaluate 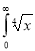
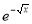 dx.
dx.
A13)
Let 
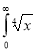
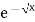 dx
dx
X | 0 | 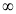 |
t | 0 |  |
Put 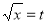 or
or 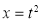 ;dx =2t dt
;dx =2t dt
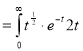 dt
dt
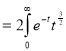 dt
dt
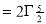
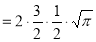
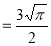
Q14) Evaluate I = 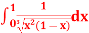
A14)
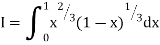
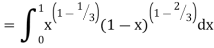

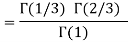
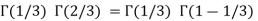
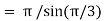
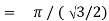
= 2 π/3
Q15) Prove that:
If 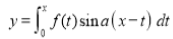 , then show that
, then show that .
.
A15)
We have given that
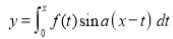 - - - - - - - - - - - - - - - - (1)
- - - - - - - - - - - - - - - - (1)
Then we have to prove that .
.
Differentiating by DUIS rule (Leibnitz’s Rule), we have

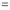
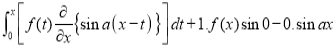
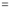
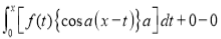
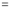
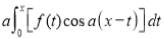
Again differentiating by DUIS rule (Leibnitz’s Rule), we have
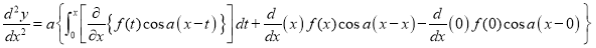
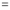
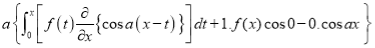
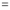
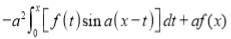
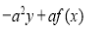
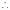
This is the desired result.
(ii)If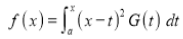 , then prove that
, then prove that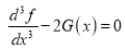 .
.
We have given that
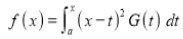 - - - - - - - - - - - - - - - - (1)
- - - - - - - - - - - - - - - - (1)
Then we have to prove that .
.
Differentiating by DUIS rule (Leibnitz’s Rule), we have
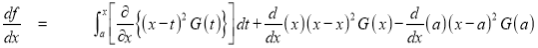
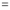

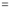
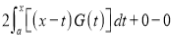
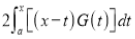
Again differentiating by DUIS rule (Leibnitz’s Rule), we have
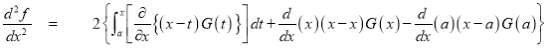
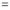
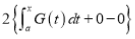
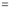
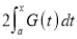
Again differentiating by DUIS rule (Leibnitz’s Rule), we have
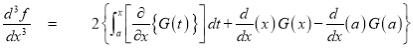
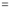
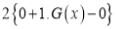
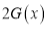
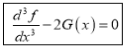
Q16) Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
A16)
Let,
y = 2 – x ………………..(1)
And y² = 2 (2 – x) ………………..(2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2) ,
We know that,
Area = 
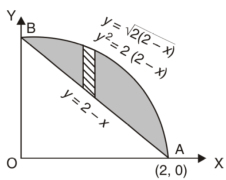
Here we will find the area as below,
Area = 
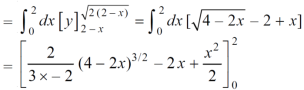
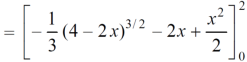
Which gives,
= ( - 4 + 4 /2 ) + 8 / 3 = 2 / 3.
Q17) Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.
A17)
We have,
r = a(1+cosθ) …………………….(1)
And
r = a ……………………………….(2)
On solving these equations by eliminating r , we get
a(1+cosθ) = a
(1+cosθ) = 1
Cosθ = 0
Here a θ varies from – π/2 to π/2
Limit of r will be a and 1+cosθ)
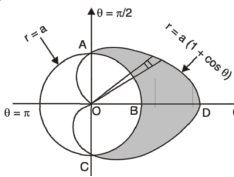
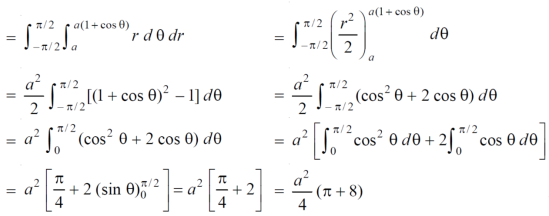
Which is the required area.
Q18) Calculate the volume generated by the revolution of a cardioid,
r = a ( 1 – cosθ) about its axis
A18)
Here, r = a ( 1 – cosθ)
Volume =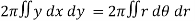
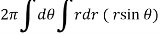
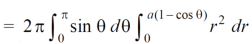
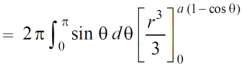
=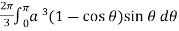
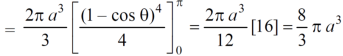
Which is the volume of generated by cardioid.
Q19) Find the area enclosed by the curves  and if the area is rotated
and if the area is rotated  about the x-axis then determine the volume of the solid of revolution.
about the x-axis then determine the volume of the solid of revolution.
A19)
We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-
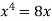
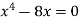
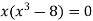
We get,
x = 0 and x = 2
The curve of the given equations will look like as follows-
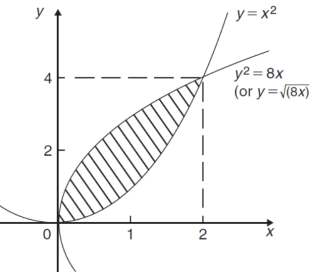
Then,
The area of the shaded region will be-
A = 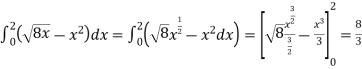
So that the area will be 8/3 square unit.
The volume will be
= (volume produced by revolving  – (volume produced by revolving
– (volume produced by revolving 
= 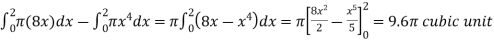
Q20) Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1 , 3].
A20)
The graph of the function f(x) = 1/x will look like-
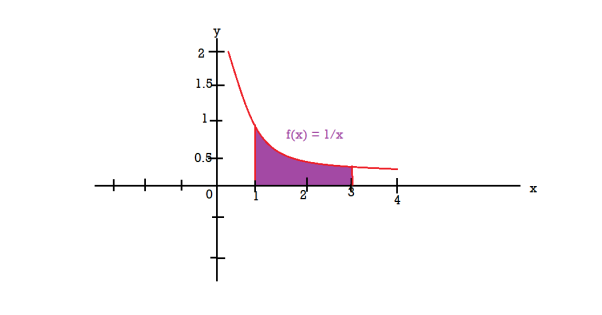
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]
Then the volume of the solid will be-
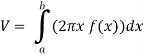
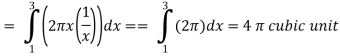
Q21) Find the mass of a plate formed by the coordinate planes and the plane-
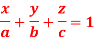
The variable density 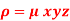
A21)
Here we the mass will be-
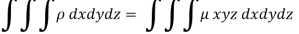
The limits of y are from y = 0 to y = b(1 – x/a) and limits of x are from 0 to a.
Therefore the required mass will be-
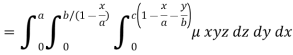
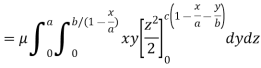
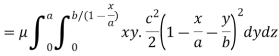
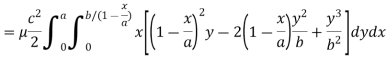
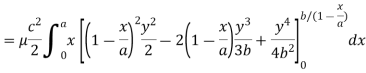
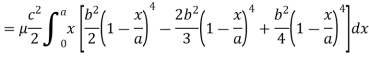

Which is the required answer.