Unit - 3
Vector Spaces
Q1) Are 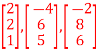 linearly independent?
linearly independent?
A1) Independent if 
Has only the trivial solution 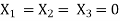


Q2) Check whether the vectors 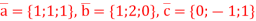 are independent.
are independent.
A2) Calculate the coefficients in which a linear combination of these vectors vector.
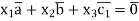
This vector equation can be written as a system of linear equations
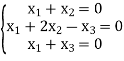
Solve this system using the gauss method
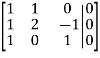
From 2 row we subtract the 1-th row; from 3row we subtract the 1-th row:
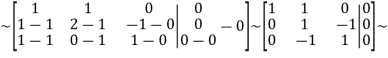
From 1 row we subtract the 2row; for 3 row add 2 row:
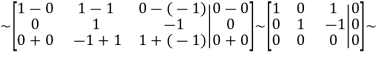
This solution shows that the system has many solutions, i.e exist nonzero combination c such that the linear combination of 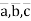 is equal to the zero vector,
is equal to the zero vector,
For Example, 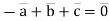
Means vectors 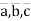 are linearly dependent.
are linearly dependent.
Answer: Vectors 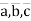 are linearly dependent.
are linearly dependent.
Q3) Is the set S = {(1,1),(1,-1)} a basis for 
- Does S span
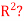 2. IS S linearly independent?
2. IS S linearly independent?
A3) Solve 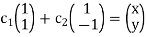
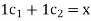
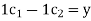
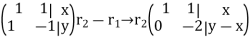
This system is consistent for every x and y, therefore S spans 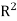
2.IS S linearly independent?
Solve
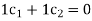
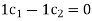

The system has a unique solution 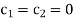 (trivial solution)
(trivial solution)
Therefore, S is linearly independent.
Consequently, S is a basis for 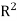
Q4)
A4) Is a basis for the vector space 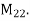
1.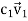 +
+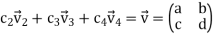
Is equivalent to:
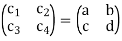
Which is consistent for every a,b,c and d.
Therefore, S spans 
2. +
+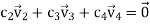 is equivalent to:
is equivalent to:
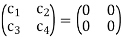
The system has only the trivial solution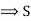 is linearly independent.
is linearly independent.
Consequently, S is a basis for 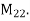
Q5) Let L: V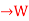 . Then ker L is a subspace of V.
. Then ker L is a subspace of V.
A5) Proof: Notice that if L(v)=0 and L(u)=0, then for any constants c,d, L(cu+dv)=0.
Then by the subspace theorem, the kernel of L is a subspace of V.
This theorem has a nice interpretation in terms of the eigenspace of L. Suppose L has a zero eigenvalue. Then the associated eigenspace consists of all vectors v such that Lv=0v=0; in other words, the 0-eigenspace of L is exactly the kernel of L
Returning to the previous example, let L(x,y) =(x+y,x+2y,y). L is clearly not surjective, Since L sends 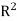 to a plane in
to a plane in 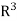 .
.
Notice that if x = L(v) and y = L(v), then for any constants c,d then cx+dy=L(cx+du). Then the subspace theorem strikes again, and we have the following theorem.
Q6)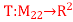 defined by
defined by  is linear. Describe its kernel and range and give the dimension of each.
is linear. Describe its kernel and range and give the dimension of each.
A6) It should be clear that  if, and only if, b= -a and d= -c. The kernel of T is therefore all matrices of the form
if, and only if, b= -a and d= -c. The kernel of T is therefore all matrices of the form
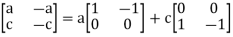
The two matrices 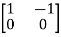 and
and 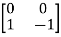 are not scalar multiples of each other, so they must be linearly independent. Therefore, the dimension of ker(T) is two.
are not scalar multiples of each other, so they must be linearly independent. Therefore, the dimension of ker(T) is two.
Now suppose that we have any vector 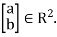 Clearly
Clearly 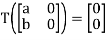 . So, the range of T of
. So, the range of T of 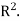 Thus the dimension of ran(T)is two.
Thus the dimension of ran(T)is two.
Q7)  defined by T(ax+b) = 2bx-a is linear. Describe its kernel and range and give the dimension of each.
defined by T(ax+b) = 2bx-a is linear. Describe its kernel and range and give the dimension of each.
A7) T(ax+b) =2bx-a=0 if, and only if, both a and b are zero. Therefore, the kernel of T is only the zero polynomial. By definition, the dimension of the subspace consisting of only the zero vector is zero, so ker(T) has dimension zero.
Suppose that we take a random polynomial cx+d in the codomain. If we consider the polynomial -dx+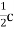 in the domain we see that
in the domain we see that
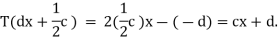
This shows that the range of T is all of 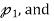 it has dimension two.
it has dimension two.
Q8) Is the given, matrix Invertible 
A8)
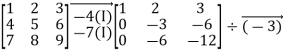

A fail to be invertible, since rref(A)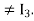
Q9) Given 3 3 Rectangular Matrix
3 Rectangular Matrix

A9) The augumented matrix is as follows
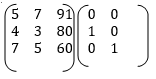
After applying the Gauss-Jordan elimination method:
The inverse of a matrix is as follows,
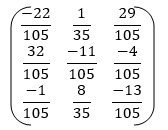
Q10) Find the inverse of

A10)
Step 1: Adjoin the identity matrix to the right side of A:
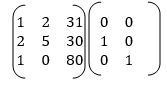
Step 2: Apply row operations to this matrix until the left side is reduced to I. The computations are:
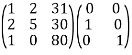 R2
R2  R2-R1 , R3
R2-R1 , R3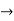 R3-R1
R3-R1
 R3
R3  R3 + 2R2
R3 + 2R2
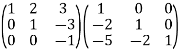 R1
R1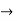 R1 -3R3 , R2
R1 -3R3 , R2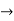 R2+3R3
R2+3R3
 R1
R1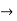 R1-2R2
R1-2R2
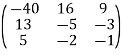
Step 3: Conclusion: The inverse matrix is:
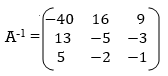
Q11) Find the inverse of matrix A given below:

A11) Let A = IA
Or
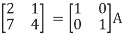

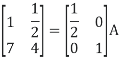

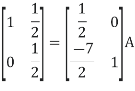
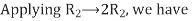
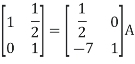

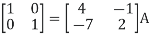
Thus, the inverse of matrix A is given by I =
Therefore,
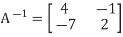
Q12) Theorem: Let ( ) be a basis of V and (
) be a basis of V and ( ) an arbitrary list of vectors in W. Then there exists a unique linear map
) an arbitrary list of vectors in W. Then there exists a unique linear map

A12) Proof: First we verify that there is at most one linear map T with 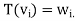 . Take any
. Take any 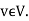 Since (
Since (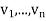 ) is a basis of V there are unique scalars
) is a basis of V there are unique scalars 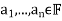 such that
such that 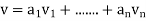 . By linearity we must have
. By linearity we must have
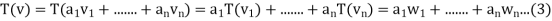
And hence T(v) is completely determined. To show existence, use (3) to define T. It remains to show that this T is linear and that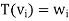 . These two conditions are not hard to show and are left to the reader.
. These two conditions are not hard to show and are left to the reader.
The set of linear maps 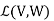 is itself a vector space. For S,T
is itself a vector space. For S,T addition is defined as
addition is defined as
(S+T)v = S v + Tv 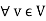
For a 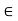 F an T
F an T 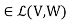 scalar multiplication is defined as
scalar multiplication is defined as
(aT)(v) = a(Tv) 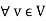
We should verify that S+T and aT are indeed linear maps again and that all properties of a vector space is satisfied.
I.e., associavity, identity and distributive property. Hence by the above properties we conclude that the given transformation is linear transformation.
Q13) Consider a linear map Tv: 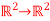 which rotates vectors be an angle 0
which rotates vectors be an angle 0  . From a known statement we have the corresponding matrix for this linear transformation is given below, solve for linear mapping
. From a known statement we have the corresponding matrix for this linear transformation is given below, solve for linear mapping

A13) the composition of two rotations b angles are given by v and v’ that is
TV’TV is clearly the rotation TV+V’ hence we must have
Av+v’ = Av’Av
The left hand side of this equation is given by
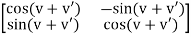
And the right hand-side is,
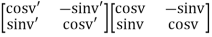 =
= 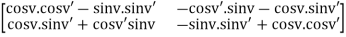
Comparing corresponding entries we find the claim that Tv’Tv = Tv+v’ is equivalent to well-known addition formulas
Cos(v+v’) = cosv. Cosv’ – sinv. Sinv’
Sin(v+v’) = cosv’. Sinv +cosv. Sinv’.
Q14) Let T  L
L  be defined by T(p(x)) = 2xp’(x), and let B1 =
be defined by T(p(x)) = 2xp’(x), and let B1 = 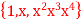 be a basis of
be a basis of 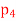 (R). Determine
(R). Determine 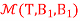
A14) First we will calculate the images of the basis vectors in B1 under the linear transformation T.
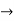 T(1) = 2x(1)’ = 2x(0) = 0(1) + 0(x) + 0(x2) + 0(x3) + 0(x4)
T(1) = 2x(1)’ = 2x(0) = 0(1) + 0(x) + 0(x2) + 0(x3) + 0(x4)
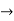 T(x) = 2x(x)’ = 2x(1) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
T(x) = 2x(x)’ = 2x(1) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
 T(x2) = 2x(x2)’ = 2x(2x) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
T(x2) = 2x(x2)’ = 2x(2x) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
 T(x3) = 2x(x3)’ = 2x(3x3) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
T(x3) = 2x(x3)’ = 2x(3x3) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
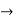 T(x4) = 2x(x4)’ = 2x (4x3) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
T(x4) = 2x(x4)’ = 2x (4x3) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
Therefore, we can now construct our matrix as follows.
The first column of 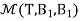 corresponds to the co-efficients determinend by T(1).
corresponds to the co-efficients determinend by T(1).
The second column corresponds to the co-efficients determined by T(x) and so fourth
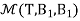 =
= 
Q15) Let T  L(M22, M22) be defined by T
L(M22, M22) be defined by T  =
= 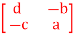 for a,b,c,d
for a,b,c,d  R and let B1 =
R and let B1 = 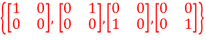 be a basis of M22.Determine
be a basis of M22.Determine 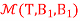
A15) we will first calculate the images of our basic vectors under T.
T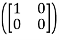 =
= 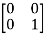 = 0
= 0 + 0
+ 0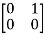 + 0
+ 0 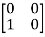 + 1
+ 1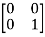
T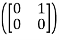 =
= 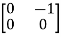 = 0
= 0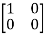 -1
-1 + 0
+ 0 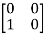 + 0
+ 0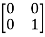
T 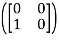 =
= 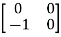 = 0
= 0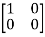 + 0
+ 0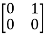 -1
-1  + 0
+ 0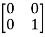
T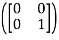 =
= 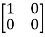 = 1
= 1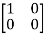 + 0
+ 0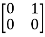 + 0
+ 0 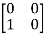 +0
+0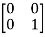
Therefore, we construct
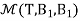 =
= 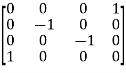
Q16) Prove that 
A16)
We have
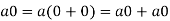
We can write 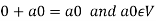
So that,
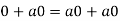
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
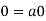
Q17) The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 
2. 
A17)
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 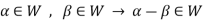
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
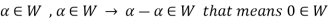
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 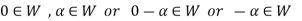
So that the additive inverse of each element of W is also in W.
So that-

Thus W is closed with respect to vector addition.
Q18) If the set S = 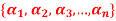 of vector V(F) is linearly independent, then none of the vectors
of vector V(F) is linearly independent, then none of the vectors 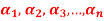 can be zero vector.
can be zero vector.
A18)
Let 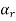 be equal to zero vector where
be equal to zero vector where 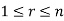
Then 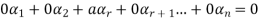
For any 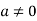 in F.
in F.
Here 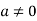 therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
Hence none of the vectors can be zero.
We can conclude that a set of vectors which contains the zero vector is necessarily linear dependent.