Unit - 2
Semiconductors
Q1) For a p-type Ge ni = 2.1x1019m-3 density of boron =3.2x1023 atoms m-3. The electron and hole mobility are 0.4 and 0.2 m2V-1s-1. Calculate conductivity before and after addition of boron?
A1) Before adding boron
 = q (p
= q (p p+n
p+n n)
n)
= ni q (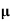 p+
p+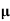 n) = 2.1x1019x1.6x10-19x(0.4+0.2)=2.016 S/m-1
n) = 2.1x1019x1.6x10-19x(0.4+0.2)=2.016 S/m-1
After adding boron
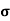 = q p
= q p p
p
= 3.2x1023x1.6x10-19x0.2=10.24x103S/m-1
Q2) Determine the density of the donor atoms which have been added to the intrinsic Ge to make it a n-type material of resistivity 0.1x10-2ohm-m. Mobility of electron in n-type semiconductor is 0.5m2V-1s-1.
A2)  = q (n
= q (n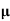 n)
n)
n=  /q
/q n
n
 = 1/
= 1/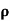
n= 1/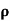 q
q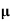 n = 1/(0.1x10-2x0.5x1.6x10-19) = 1.25x1022m-3
n = 1/(0.1x10-2x0.5x1.6x10-19) = 1.25x1022m-3
Q3) The intrinsic carrier density at room temperature in Ge is 3.4x1019m-3. If electron and hole mobilities are 0.4 and 0.2 m2V-1s-1 respectively. Calculate its resistivity?
A3) 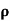 = 1/
= 1/
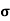 =ni q (
=ni q (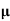 p+
p+ n) = 3.4x1019x 1.6x10-19(0.4+0.2) = 3.264S/m-1
n) = 3.4x1019x 1.6x10-19(0.4+0.2) = 3.264S/m-1
 = 1/
= 1/ = 1/3.264 = 0.31ohm-m
= 1/3.264 = 0.31ohm-m
Q4) The electron and hole mobilities in In-Sb are 6 and 0.2 m2V-1s-1 respectively. At room temperature resistivity of In-Sb is 2x10-4ohm-m. Find intrinsic carrier concentration assuming the material to be intrinsic?
A4) 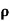 = 1/
= 1/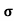
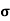 =ni q (
=ni q ( p+
p+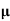 n)
n)
ni = 1/ 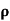 q (
q (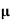 p+
p+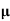 n) = 1/2x10-4x1.6x10-19(6+0.2) = 5.04x1021m-3
n) = 1/2x10-4x1.6x10-19(6+0.2) = 5.04x1021m-3
Q5) An electric field of 90Vm-1 is applied to n-type semiconductor. Determine the current density in sample given electron mobility 0.4 m2V-1s-1, n=5.9x1020m-3?
A5) J= E
E
 = nq
= nq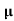 n = 5.9x1020x1.6x10-19x0.4=37.36S/m-1
n = 5.9x1020x1.6x10-19x0.4=37.36S/m-1
J=3.39x103
Q6) Determine the density of the donor atoms which have been added to the intrinsic Ge to make it a n-type material of resistivity 0.5x10-2ohm-m. Mobility of electron in n-type semiconductor is 0.8m2V-1s-1.
A6) 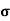 = q (n
= q (n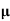 n)
n)
n= 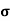 /q
/q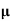 n
n
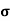 = 1/
= 1/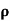
n= 1/ q
q n = 1/(0.5x10-2x0.8x1.6x10-19) = 1.56x1021m-3
n = 1/(0.5x10-2x0.8x1.6x10-19) = 1.56x1021m-3
Q7) Calculate the drift current density in a semiconductor for a given electric field. For germanium sample at T=300oK where ND = 0 and NA =1x1015 cm-3 ni = 2.4x1013 cm-3. Assume electron and hole mobility to be 3900 cm2/V-sec and 1900 cm2/V-sec. Applied electric field is E= 40V/cm?
A7) As NA>>ND
p0 = ½ {(NA- ND) + (NA- ND)2+4ni2)1/2}
p0 = 5x1014cm-3
n= ni2/NA
n= 5.76x1011cm-3
J = q (p p+n
p+n n) E
n) E
For extrinsic p-type semiconductor
J = q NA p E =1.6x10-19x1900x1015x40 =12.16 A/cm2
p E =1.6x10-19x1900x1015x40 =12.16 A/cm2
Q8) The resistance of a wire is 20 Ω. What will be new resistance, if it is stretched uniformly 8 times its original length?
A8) R1 = 20 Ω, R2=?
Let the original length (l1) be l.
The new length, l2 = 8l1 (i.e) l2 =8l
The original resistance, R = ρ [ l1 / A1]
The new resistance
R2 = 
Though the wire is stretched, its volume is unchanged.
Initial volume = Final volume
A1l1= A2l2 , A1l = A28l
A1 / A2 = 8l / l = 8
By dividing equation R2 by equation R1, we get

Substituting the value of A1/A2, we get
R2 / R1 = 8 ×8 = 64 2
R2 = 64 × 20=1280 Ω
Hence, stretching the length of the wire has increased its resistance.
Q9) Consider a rectangular block of metal of height A, width B and length C as shown in the figure.
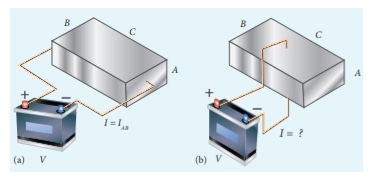
If a potential difference of V is applied between the two faces A and B of the block (figure (a)), the current IAB is observed. Find the current that flows if the same potential difference V is applied between the two faces B and C of the block (figure (b)). Give your answers in terms of IAB.
A9)
In the first case, the resistance of the block

Q10) Compute the resistivity of the given material whose resistance is 2 Ω; area of cross-section and length are 25cm2 and 15 cm respectively?
A10)
Given
R = 2 Ω
l = 15 cm = 0.15 m
A = 25 cm2 = 0.25 m2
Resistivity formula is
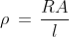
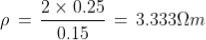
Q11) The length and area of wire are given as 0.2 m and 0.5 m2 respectively. The resistance of that wire is 3 Ω, calculate the resistivity?
A11)
Given
R = 3 Ω
l = 0.2 m and
A = 0.5 m2
Resistivity formula is


Q12) Determine thermal equilibrium of electron and hole concentration for an n-type silicon semiconductor at T=300oK where ND = 1x1016cm-3 and NA =0. Assume ni = 1.5 x 1010cm-3?
A12) The majority carrier concentration
n0 = ½ {(ND- NA) + (ND- NA)2+4ni2)1/2}
n0 = 1016 cm-3
The minority carrier concentration
p0 = ni2/ND
p0 = 2.25x x104 cm-3
Q13) Determine thermal equilibrium of electron and hole concentration for doping concentration at T=300oK where ND = 4x1013cm-3 and NA =0. Assume ni = 2.4 x 1013cm-3?
A13) The majority carrier concentration
n0 = ½ {(ND- NA) + (ND- NA)2+4ni2)1/2}
n0 =3.12x1013 cm-3
The minority carrier concentration
p0 = ni2/ND
p0 = 1.45x x1013 cm-3
Q14) Determine thermal equilibrium of electron and hole concentration in n-type semiconductor at T=300oK where ND = 2x1016cm-3 and NA =12x1015 cm-3. Assume ni = 1.5 x 1010cm-3?
A14) The majority carrier concentration
n0 = ½ {(ND- NA) + (ND- NA)2+4ni2)1/2}
n0 =4x1015 cm-3
The minority carrier concentration
p0 = ni2/ND
p0 = 11.25x x103 cm-3
Q15) The intrinsic carrier density is 1.5 × 1016 m–3. If the mobility of electron and hole are 0.13 and 0.05 m2 V–1 s–1, calculate the conductivity.
A15)
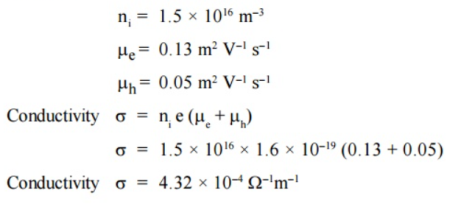
Q16) The Intrinsic carrier density at room temperature in Ge is 2.37 × 1019 m3 if the electron and hole mobilities are 0.38 and 0.18 m2 V–1 s–1 respectively, calculate the resistivity.
A16)
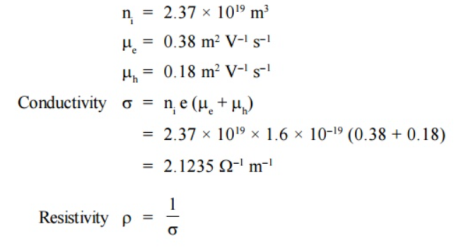
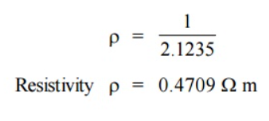
Q17) In a P-type germanium, ni = 2.1 × 1019 m–3density of boran 4.5 × 1023 atoms /m3. The electron and hole mobility are 0.4 and 0.2 m2 v–1 s–1 respectively. What is its conductivity before and after addition of boron atoms.
A17)

Q18) For an intrinsic Semiconductor with a band gap of 0.7 eV, determine the position of EF at T = 300 K if m*h = 6m*e.
A18)

Q19) Find the resistance of an intrinsic Ge rod 1 mm long, 1 mm wide and 1 mm thick at 300 K. The intrinsic carrier density 2.5 ×1019 m–3 is at 300 K and the mobility of electron and hole are 0.39 and 0.19 m2 v–1 s–1.
A19)

Q20) The intrinsic carrier density of a semiconductor is 2.1 × 1019 m–3. The electron and hole mobilities are 0.4 and 0.2 m2 V–1 s–1 respectively. Calculate the conductivity.
A20)

Q21) What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?
A21)
(a)For the electron:
Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s.
Then, momentum
p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s)
p = 4.92 × 10–24 kg m/s
De Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s
λ= 0.135 nm
(b)For the ball:
Mass m’ = 0.150 kg,
Speed v ’= 30.0 m/s.
Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s)
p’= 4.50 kg m/s
De Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m
The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement.
Q22) What is the de Broglie wavelength associated with an electron, accelerated through a potential difference of 100 volts?
A22)
Accelerating potential V = 100 V. The de Broglie wavelength λ is
λ= h /p = 1 227/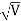 nm
nm
λ.1 227/ nm = 0.123 nm
nm = 0.123 nm
The de Broglie wavelength associated with an electron in this case is of the order of x ray wavelengths.
Q23) What is Heisenberg’s Uncertainty Principle?
A23)
According to classical physics, given the initial conditions and the forces acting on a system, the future behaviour (unique path) of this physical system can be determined exactly. That is, if the initial coordinates , velocity
, velocity  , and all the forces acting on the particle are known, the position
, and all the forces acting on the particle are known, the position  , and velocity
, and velocity  are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.
are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.
Does this hold for the microphysical world?
Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle.
In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:

This principle indicates that, although it is possible to measure the momentum or position of a particle accurately, it is not possible to measure these two observables simultaneously to an arbitrary accuracy. That is, we cannot localize a microscopic particle without giving to it a rather large momentum.
We cannot measure the position without disturbing it; there is no way to carry out such a measurement passively as it is bound to change the momentum.
To understand this, consider measuring the position of a macroscopic object (you can consider a car) and the position of a microscopic system (you can consider an electron in an atom). On the one hand, to locate the position of a macroscopic object, you need simply to observe it; the light that strikes it and gets reflected to the detector (your eyes or a measuring device) can in no measurable way affect the motion of the object.
On the other hand, to measure the position of an electron in an atom, you must use radiation of very short wavelength (the size of the atom). The energy of this radiation is high enough to change tremendously the momentum of the electron; the mere observation of the electron affects its motion so much that it can knock it entirely out of its orbit.
It is therefore impossible to determine the position and the momentum simultaneously to arbitrary accuracy. If a particle were localized, its wave function would become zero everywhere else and its wave would then have a very short wavelength.
Q24) The uncertainty in the momentum of a ball travelling at 20m/s is 1×10−6 of its momentum. Calculate the uncertainty in position? Mass of the ball is given as 0.5kg.
A24)
Given
v = 20m/s,
m = 0.5kg,
h = 6.626 × 10-34 m2 kg / s
Δp =p×1×10−6
As we know that,
P = m×v = 0.5×20 = 10kgm/s
Δp = 10×1×10−6
Δp = 10-5
Heisenberg Uncertainty principle formula is given as,
∆x∆p 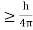
∆x 
∆x 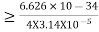
∆x =0.527 x 10-29 m
Q25) Prove non-existence of electrons in the nucleus?
A25)
One of the applications is to prove that electron cannot exist inside the nucleus.
But to prove it, let us assume that electrons exist in the nucleus.
As the radius of the nucleus in approximately 10-14m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by
According to uncertainty principle
∆x ∆p =h/2π
Thus ∆p=h/2π∆x
Or ∆p=6.62 x10-34/2 x 3.14 x 10-14
Or ∆p=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron then the momentum of electron should be at least of this order that is p=1.05*10-20 kg m/sec.
An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formula
E = 
Therefore, if the electron exists in the nucleus, it should have an energy of the order of 19.6 MeV.
However, it is observed that beta-particles (electrons) ejected from the nucleus during b – decay have energies of approximately 3 Me V, which is quite different from the calculated value of 19.6 MeV.
Another reason that electron cannot exist inside the nucleus is that experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.
Therefore, it is confirmed that electrons do not exist inside the nucleus.
Q26) Discuss applications of Heisenberg uncertainty principle?
A26)
The Heisenberg uncertainty principle based on quantum physics explains a number of facts which could not be explained by classical physics.
- Non-existence of electrons in the nucleus
One of the applications is to prove that electron cannot exist inside the nucleus.
But to prove it, let us assume that electrons exist in the nucleus.
As the radius of the nucleus in approximately 10-14m. If electron is to exist inside the nucleus, then uncertainty in the position of the electron is given by
According to uncertainty principle
∆x ∆p =h/2π
Thus ∆p=h/2π∆x
Or ∆p=6.62 x10-34/2 x 3.14 x 10-14
Or ∆p=1.05 x 10-20 kg m/ sec
If this is p the uncertainty in the momentum of electron then the momentum of electron should be at least of this order that is p=1.05*10-20 kg m/sec.
An electron having this much high momentum must have a velocity comparable to the velocity of light. Thus, its energy should be calculated by the following relativistic formula
E = 
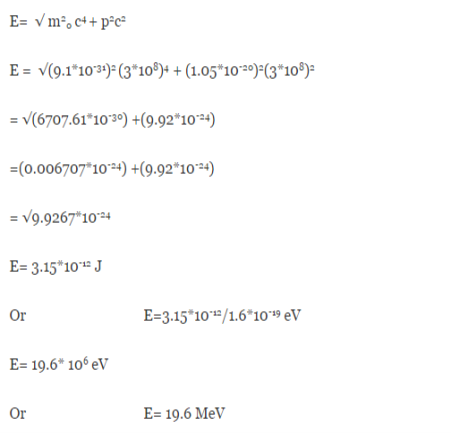
Therefore, if the electron exists in the nucleus, it should have an energy of the order of 19.6 MeV.
However, it is observed that beta-particles (electrons) ejected from the nucleus during b – decay have energies of approximately 3 Me V, which is quite different from the calculated value of 19.6 MeV.
Another reason that electron cannot exist inside the nucleus is that experimental results show that no electron or particle in the atom possess energy greater than 4 MeV.
Therefore, it is confirmed that electrons do not exist inside the nucleus.
2. Calculation of zero-point energy
The minimum energy of a system at o k (zero kelvin) is called zero-point energy.
Consider a particle which is confined to move under the influence of potential of dimensions a. Since the particle may be present anywhere in these dimensions, so uncertainty in position
∆x = a/2 (half the diameter).
According to uncertainty principle
∆x∆px = ℏ/2
Or
Thus ∆px= ℏ /2∆x
∆px= ℏ /2a/2 = ℏ /a
Uncertainty in momentum of particle along x-axis is
∆px= ℏ /a
Assuming the momentum of particle to be at least equal to uncertainty in it, the lowest possible value of K.E. Of particle is given by
K.E. = 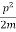 =
=  =
=
Where m is the mass of the particle.
Energy even at O K is given by the above equation. This minimum energy is called the zero-point energy.
This implies that even at zero kelvin, the particle is never at rest. If it is so, then ∆pX = 0, which is not possible. [It gives ∆x = ∞]
3. Existence of proton, neutron and alpha particles within the nucleus.
We know that the rest mass of the protons and neutron is of the order of
1.67x 10-27 kg. Hence, the value of momentum 5.27 x 10-21 kg-m/sec from calculation and also the value of v come out to be 3x 105m/sec.
The corresponding value of kinetic energy of a neutron or a proton is
E =  =8.33 x 10-15J =
=8.33 x 10-15J = eV
eV
 52.05 keV
52.05 keV
Since the rest mass of the a-particle is nearly four times the proton mass, therefore the alpha particle should have a minimum kinetic energy of one fourth of 52.05 keV, or about 13 keV. Since the energy carried by the protons or neutrons emitted by the nuclei are greater than 52 keV and for a-particle more than 13 keV, these particles can exist in the nuclei.
4. Size of Elementary cell in Phase space
We have studied in our previous class that state of a microsystem is defined by six variables – three are due to position and three due to momentum.
Hence, a system of N particles needs 6 N variables
If ∆ x and ∆px be the uncertainly in position and in momentum measurements then
∆ x ∆ px =  ;
;
Similarly, ∆ y ∆ py =  ,
,
And ∆ z ∆ pz =  ,
,
Multiplying these three equations, we get
∆ x ∆ y ∆ z ∆ px ∆ py ∆ pz = (  )3 in the units (J3 S3).
)3 in the units (J3 S3).
The above product is called the volume of elementary cell in phase space.
So, volume of an elementary cell in phase space  10-101 units, (for quantum statistics) being
10-101 units, (for quantum statistics) being 
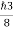 .
.
5. Accurate limit of frequency of radiation emitted by an atom
Consider the radiation emitted from an excited atom. The energy of this atom will decrease when it emits one or more photons of characteristic frequency.
The average period between excitation of the atom and the release of energy is about 10-8 seconds.
Thus, uncertainly in energy is
∆ E 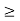
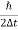
Or ∆ E 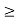
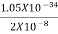 J
J
Or ∆ E 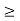 5.3 x 10-27 J
5.3 x 10-27 J
Frequency of light is uncertain by
∆ ν = 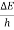 =
= 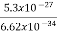 Hz
Hz  0.8 x 107 Hz
0.8 x 107 Hz
As a result, the radiation from an excited atom does not have the noted precise frequency new ν - ∆ ν and ν + ∆ ν.
Q27) Derive the Schrodinger wave equation?
A27)
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So, we have
E= K+V = mv2+V(x) =
mv2+V(x) =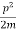 +V(x) ……….. (1)
+V(x) ……….. (1)
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk.
Using this equation (1) for the energy will become
ℏω =  + V(x) ……….. (2)
+ V(x) ……….. (2)
A wave with frequency ω and wave number k can be written as usual as
Ψ (x, t) =Aei(kx−ωt) ……….. (3)
The above equation is for one dimensional and for three dimensional we can write it as
ψ (r, t) =Aei(k·r−ωt) ……….. (4)
But here we will stick to one dimension only.
 =−iωψ ⇒ ωψ=
=−iωψ ⇒ ωψ=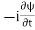 ……….. (5)
……….. (5)
 =−k2ψ ⇒ k2ψ = -
=−k2ψ ⇒ k2ψ = -  ……….. (6)
……….. (6)
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain
ℏ(ωψ) = 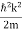 ψ+ V(x) ψ ⇒
ψ+ V(x) ψ ⇒  = -
= - 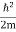
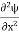 + V(x) ψ ……….. (7)
+ V(x) ψ ……….. (7)
This is the time-dependent Schrodinger equation.
If we put the x and t in above equation then equation (7) takes the form as given below
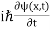 = -
= - 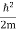
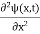 + V(x) ψ(x,t) ……….. (8)
+ V(x) ψ(x,t) ……….. (8)
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the 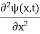 term becomes ∇2ψ.
term becomes ∇2ψ.
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However, we already know the solution as we used this function ψ (x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
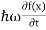 = -
= - 
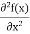 + V(x) f(x) ……….. (9)
+ V(x) f(x) ……….. (9)
We already know that E=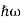 . However, ψ (x, t) is general convention to also use the letter ψ to denote the spatial part. So, we will now replace f(x) with ψ(x)
. However, ψ (x, t) is general convention to also use the letter ψ to denote the spatial part. So, we will now replace f(x) with ψ(x)
Eψ = - 
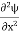 + V(x) ψ ……….. (10)
+ V(x) ψ ……….. (10)
This is called the time-independent Schrodinger equation.
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.
All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics.
Q28) The mass of an electron is 9.1×10–31 kg. Its uncertainty in velocity is 5.7×105 m/sec. Calculate uncertainty in its position?
A28)
Given m= 9×10–31
ΔV= 5.7×105 m/sec
Δx=?
h= 6.6×10–34 Joule-Sec.
Δx.Δv ≥h/4πm
Δx≥h/4πmΔv
≥6.6×10–34/9×3.14×9.1×10–31×5.7×105
≥ 0.010×10–8
≥ 1×10–10m
Q29) The mass of a ball is 0.15 kg & its uncertainty in position to 10–10m. What is the value of uncertainty in its velocity?
A29)
Given
m=0.15 kg.
h=6.6×10-34 Joule-Sec.
Δx = 10 –10 m
Δv=?
Δx.Δv ≥h/4πm
Δv≥h/4πmΔx
≥6.6×10-34/4×3.14×0.15×10–10
≥ 3.50×10–24m
Q30) The mass of a bullet is 10gm & uncertainty in its velocity is 5.25×10–26 cm/sec. Calculate the uncertainty in its position?
A30)
m=10 gm. h=6.6×10–27 erg-sec
Δv= 5.25×10–26 cm
Δx=?
Δx.Δv ≥h/4πm
Δx≥h/4πmΔv
≥6.6×10-34/4×3.14×10×5.25×10–26
≥ 0.10×10–2m
≥ 1×10–3 cm