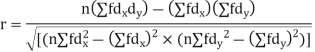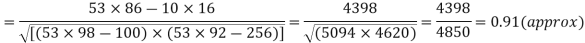Unit - 5
Probability & Statistics
Q1) Define the null and alternative hypothesis.
A1)
Simple and composite hypotheses-
If a hypothesis specifies only one value or exact value of the population parameter then it is known as a simple hypothesis., and if a hypothesis specifies not just one value but a range of values that the population parameter may assume is called a composite hypothesis.
The null and alternative hypothesis
The hypothesis is to be tested as called the null hypothesis.
The hypothesis which complements the null hypothesis is called the alternative hypothesis.
In the example of a car, the claim is 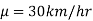 , and its complement is
, and its complement is 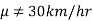 .
.
The null and alternative hypothesis can be formulated as-
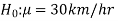
And
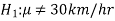
Q2) Define two types of error.
A2)
Type-1 and Type-2 error-
Type-1 error-
The decision relating to the rejection of null hypo. When it is true is called a type-1 error.
The probability of type-1 error is called the size of the test, it is denoted by  , and defined as-
, and defined as-

Note-
 is the probability of a correct decision.
is the probability of a correct decision.
Type-2 error-
The decision relating to the non-rejection of null hypo. When it is false is called a type-1 error.
It is denoted by 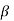 and defined as-
and defined as-

Decision |
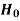 | 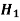 |
Reject 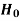 | Type-1 error | Correct decision |
Do not reject 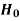 | Correct decision | Type-2 error |
Q3) How do we test the hypothesis for the population mean by using Z-test.
A3)
For testing the null hypothesis, the test statistic Z is given as-
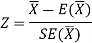

The sampling distribution of the test statistics depends upon variance 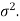
So that there are two cases-
Case-1: when 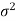 is known -
is known -
The test statistic follows the normal distribution with mean 0, and variance unity when the sample size is large as the population under study is normal or non-normal. If the sample size is small then test statistic Z follows the normal distribution only when the population under study is normal. Thus,

Case-2: when 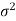 is unknown –
is unknown –
We estimate the value of 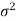 by using the value of sample variance
by using the value of sample variance
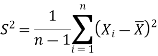
Then the test statistic becomes-
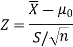
After that, we calculate the value of the test statistic as may be the case (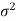 is known or unknown), and compare it with the critical value at the prefixed level of significance α.
is known or unknown), and compare it with the critical value at the prefixed level of significance α.
Q4) A manufacturer of ballpoint pens claims that a certain pen manufactured by him has a mean writing-life of at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with a standard deviation of 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at a 1% level of significance?
A4)
It is given that-
The specified value of the population mean =  = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25
The null and alternative hypothesis will be-
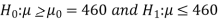
Also, the alternative hypothesis left-tailed so that the test is left tailed test.
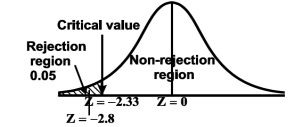
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should use a t-test for if the writing-life of the pen follows a normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by


We get the critical value of left tailed Z test at 1% level of significance is 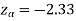
Since the calculated value of test statistic Z (= ‒2.8,) is less than the critical value
(= −2.33), that means the calculated value of test statistic Z lies in the rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at a 1% level of significance.
Q5) A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has an average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with a standard deviation of 90 hours. Should the company accept the new brand at a 5% level of significance?
A5)
Here we have-
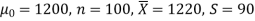
The company may accept the new CFL light when the average life of
CFL light is greater than 1200 hours. So the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So our claim is 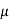 > 1200 and its complement is
> 1200 and its complement is 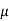 ≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,

Since the alternative hypothesis is right-tailed so the test is right-tailed.
Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use a t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for a Z-test instead of a t-test.
Therefore, the test statistic is given by
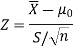
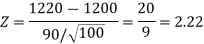
The critical values for a right-tailed test at a 5% level of significance is
 1.645
1.645
Since the calculated value of test statistic Z (= 2.22) is greater than the critical value (= 1.645), that means it lies in the rejection region so we reject the null hypothesis and support the alternative hypothesis i.e. we support our claim at a 5% level of significance
Thus, we conclude that the sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs
Q6) A tyre manufacturer claims that the average life of a particular category of his tyre is 18000 km when used under normal driving conditions. A random sample of 16 tyres was tested. The mean and SD of life of the tyres in the sample were 20000 km and 6000 km respectively.
Assuming that the life of the tyres is normally distributed, test the claim of the manufacturer at a 1% level of significance using the appropriate test.
A6)
Here we have-
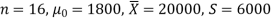
We want to test that manufacturer’s claim is true that the average
Life (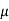 ) of tyres is 18000 km. So claim is μ = 18000 and its complement
) of tyres is 18000 km. So claim is μ = 18000 and its complement
Is μ ≠ 18000. Since the claim contains the equality sign so we can take
The claim as the null hypothesis and complement as the alternative
Hypothesis. Thus,

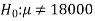
Here, population SD is unknown and the population under study is given to
Be normal.
So here can use t-test-
For testing the null hypothesis, the test statistic t is given by-
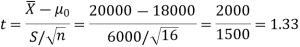
The critical value of test statistic t for two-tailed test corresponding (n-1) = 15 df at 1% level of significance are 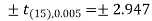
Since the calculated value of test statistic t (= 1.33) is less than the critical (tabulated) value (= 2.947) and greater than that critical value (= − 2.947), that means the calculated value of test statistic lies in the non-rejection region, so we do not reject the null hypothesis. We conclude that the sample fails to provide sufficient evidence against the claim so we may assume that manufacturer’s claim is true.
Q7) Two sources of raw materials are under consideration by a bulb manufacturing company. Both sources seem to have similar characteristics but the company is not sure about their respective uniformity. A sample of 12 lots from source A yields a variance of 125 and a sample of 10 lots from source B yields a variance of 112. Is it likely that the variance of source A significantly differs from the variance of source B at significance level α = 0.01?
A7)
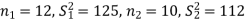
The null and alternative hypothesis will be-
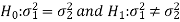
Since the alternative hypothesis is two-tailed so the test is two-tailed.
Here, we want to test the hypothesis about two population variances and sample sizes 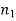 = 12(< 30) and
= 12(< 30) and 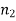 = 10 (< 30) are small. Also, populations under study are normal and both samples are independent.
= 10 (< 30) are small. Also, populations under study are normal and both samples are independent.
So we can go for F-test for two population variances.
The test statistic is-
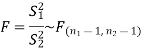
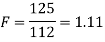
The critical (tabulated) value of test statistic F for the two-tailed test corresponding 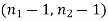 = (11, 9) df at 5% level of significance are
= (11, 9) df at 5% level of significance are 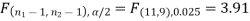 and
and
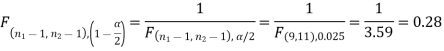
Since the calculated value of test statistic (= 1.11) is less than the critical value (= 3.91) and greater than the critical value (= 0.28), that means the calculated value of test statistic lies in the non-rejection region, so we do not reject the null hypothesis and reject the alternative hypothesis. We conclude that samples provide us sufficient evidence against the claim so we may assume that the variances of source A and B differ.
Q8) In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
A8)
The corresponding frequencies are
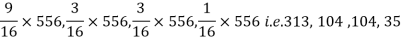
Hence,
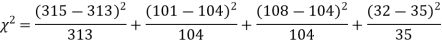
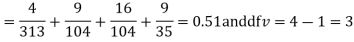
For v = 3, we have 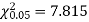
Since the calculated value of 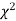 is much less than
is much less than 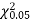 there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
For v = 3, we have 
Since the calculated value of 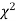 is much less than
is much less than 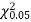 there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
Q9) Find the mean deviation of the following frequency distribution.
Class | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
Frequency | 8 | 10 | 12 | 9 | 5 |
A9) Let 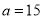
Class | Mid value 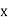 | Frequency 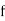 |  | 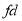 | 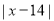 | 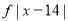 |
0-6 6-12 12-18 18-24 24-30 | 3 9 15 21 27 | 8 10 12 9 5 | -12 -6 0 6 12 | -96 -60 0 54 60 | 11 5 1 7 13 | 88 50 12 63 65 |
Total |
| 44 |
| -42 |
| 278 |
Mean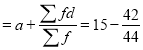
Average deviation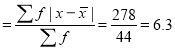
Q10) Find the value of Median from the following data.
No.of days for which absent (less than) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
No.of students | 29 | 224 | 465 | 582 | 634 | 644 | 650 | 653 | 655 |
A10) The given cumulative frequency distribution will first be converted into ordinary frequency as under
Class Interval | Cumulative frequency | Ordinary frequency |
0-5 5-10 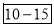 15-20 20-25 25-35 30-35 35-40 40-45 | 29  465 582 634 644 650 653 655 | 29=29 224-29=195 465-224= 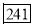 582-465=117 634-582=52 644-634=10 650-644=6 653-650=3 655-653=2 |
Median= size of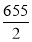 or 327.5th item
or 327.5th item
327.5th item lies in 10-15 which is the median class.
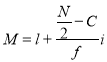
Where 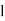 stands for lower limit of median class,
stands for lower limit of median class,
N stands for the total frequency,
C stands for the cumulative frequency just preceding the median class,
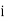 Stand’s for class interval
Stand’s for class interval
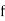 Stand’s for frequency for the median class.
Stand’s for frequency for the median class.
Median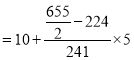
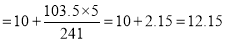
Q11) Calculate the median, quartiles and the quartile coefficient of Skewness from the following data:
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 |
No. Of Persons | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
A11) Here total frequency .
.
The cumulative frequency table is
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 |
 | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
 | 12 | 30 | 65 | 107 | 157 | 202 | 222 | 230 |
Now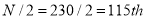 item which lies in 110-120 group.
item which lies in 110-120 group.
 Median or
Median or 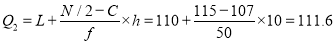
Also 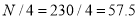 i.e.
i.e. 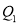 is
is 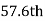 or
or 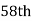 item which lies in 90-100 group.
item which lies in 90-100 group.
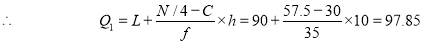
Similarly, 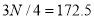 i.e.,
i.e.,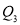 is
is 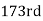 item which lies in 120-130 group.
item which lies in 120-130 group.
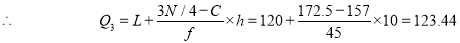
Hence quartile coefficient of skewness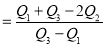
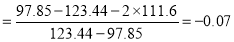 (approx.)
(approx.)
Q12) Psychological tests of intelligence and of engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and engineering ratio (E.R). Calculate the co-efficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R | 105 | 104 | 102 | 101 | 99 | 98 | 96 | 92 | 93 | 92 |
E.R | 101 | 103 | 100 | 98 | 96 | 104 | 92 | 94 | 97 | 94 |
A12) We construct the following table:
Student | Intelligence ratio 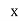 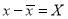 | Engineering ratio  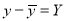 |  | 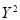 | 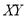 |
A B C D E F G H I J | 100 6 104 5 102 3 101 2 100 1 99 0 98 -1 96 -3 93 -6 92 -7 | 101 3 103 5 100 2 98 0 95 -3 96 -2 104 6 92 -6 97 -1 94 -4 | 36 25 9 4 1 0 1 9 36 49 | 9 25 4 0 9 4 36 36 1 16 | 18 25 6 0 -3 0 -6 18 6 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, mean of 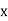 i.e.,
i.e., 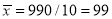 and mean of
and mean of 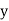 , i.e.,
, i.e., 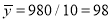
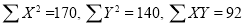
Substituting these values in the formula (1), we have
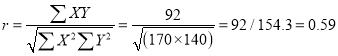
Q13) In a partially destroyed laboratory record, only the lines of regression of y on x and x on y are available as 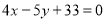 and
and  respectively. Calculate
respectively. Calculate 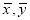 and the coefficient of correlation between x and y.
and the coefficient of correlation between x and y.
A13) Since the regression lines pass through , therefore,
, therefore,
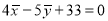 ,
, 
Solving these equations, we get 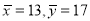
Rewriting the line of regression of y on x as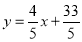 , we get
, we get
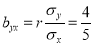 …. (i)
…. (i)
Rewriting the line of regression of x on y as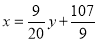 , we get
, we get
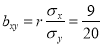 …. (ii)
…. (ii)
Multiplying (i) and (ii), we get
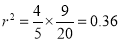

Hence 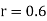 , the positive sign being taken as
, the positive sign being taken as 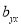 and
and 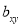 both are positive.
both are positive.
Q14) Explain Moments, Skewness and Kurtosis
A14)
MOMENT GENERATING FUNCTION
The moment generating function of the variate 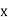 about
about 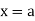 is defined as the expected value of
is defined as the expected value of 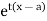 and is denoted
and is denoted  .
.
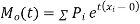
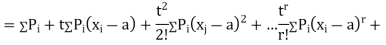
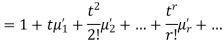
Where 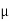 , ‘ is the moment of order
, ‘ is the moment of order 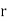 about
about 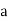
Hence 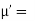 coefficient of
coefficient of  or
or 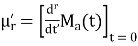
Again 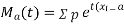 )
) 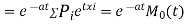
Thus the moment generating function about the point 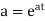 moment generating function about the origin.
moment generating function about the origin.
SKEWNESS:
Skewness denotes the opposite of symmetry. It is lack of symmetry. In a symmetrical series, the mode, the median, and the arithmetic average are identical.
Coefficient of skewness 
KURTOSIS: It measures the degree of peakedness of a distribution and is given by Measure of kurtosis.
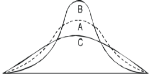
Negative skewness Positive skewness A: Mesokurtic B: Leptokurtic
C: Playkurtic
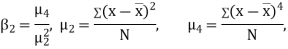
If 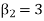 , the curve is normal or mesokurtic.
, the curve is normal or mesokurtic.
If 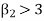 , the curve is peaked or leptokurtic.
, the curve is peaked or leptokurtic.
If 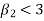 , the curve is flat topped or platykurtic
, the curve is flat topped or platykurtic
Q15) The first four moments about the working mean 28.5 of distribution are 0.2 94, 7.1 44, 42.409 and 454.98. Calculate the moments about the mean. Also evaluate 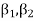 and comment upon the skewness and kurtosis of the distribution.
and comment upon the skewness and kurtosis of the distribution.
A15)
The first four moments about the arbitrary origin 28.5 are 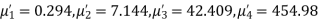
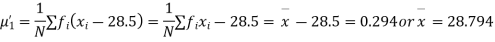
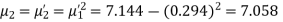
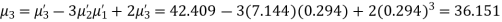
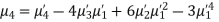
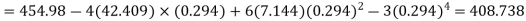
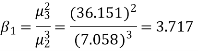
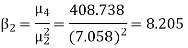
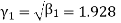 , which indicates considerable skewness of the distribution.
, which indicates considerable skewness of the distribution.
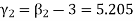 , which shows that the distribution is leptokurtic.
, which shows that the distribution is leptokurtic.
Q16) Calculate the median, quartiles and the quartile coefficient of skewness from the following data:
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
No. Of persons | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
A16)
Here total frequency 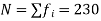
The cumulative frequency table is
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
Frequency | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Cumulative Frequency | 12 | 30 | 65 | 107 | 157 | 202 | 222 | 230 |
Now, N/2 =230/2= 115th item which lies in 110 – 120 group.
Median or 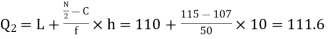
Also, 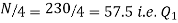 is 57.5th or 58th item which lies in 90-100 group.
is 57.5th or 58th item which lies in 90-100 group.
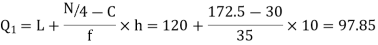
Similarly 3N/4 = 172.5 i.e. 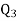 is 173rd item which lies in 120-130 group.
is 173rd item which lies in 120-130 group.

Hence quartile coefficient of skewness = 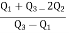
Q17) The correlation table given below shows that the ages of husband and wife of 53 married couples living together on the census night of 1991. Calculate the coefficient of correlation between the age of the husband and that of the wife.
Age of husband | Age of wife | Total | ||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | |||
15-25 | 1 | 1 | - | - | - | - | 2 | |
25-35 | 2 | 12 | 1 | - | - | - | 15 | |
35-45 | - | 4 | 10 | 1 | - | - | 15 | |
45-55 | - | - | 3 | 6 | 1 | - | 10 | |
55-65 | - | - | - | 2 | 4 | 2 | 8 | |
65-75 | - | - | - | - | 1 | 2 | 3 | |
Total | 3 | 17 | 14 | 9 | 6 | 4 | 53 | |
A17)
Age of husband | Age of wife x series | Suppose 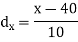  | |||||||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
Total f | |||||||
Years | Midpoint x | 20 | 30 | 40 | 50 | 60 | 70 | ||||||
Age group | Midpoint y |
|
| -20 | -10 | 0 | 10 | 20 | 30 |  | 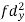 | 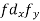 | |
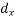  | -2 | -1 | 0 | 1 | 2 | 3 | |||||||
15-25 | 20 | -20 | -2 | 4 1 | 2 1 |
|
|
|
| 2 | -4 | 8 | 6 |
25-35 | 30 | -10 | -1 | 4 2 | 12 12 | 0 1 |
|
|
| 15 | -15 | 15 | 16 |
35-45 | 40 | 0 | 0 |
| 0 4 | 0 10 | 0 1 |
|
| 15 | 0 | 0 | 0 |
45-55 | 50 |
|
|
|
| 0 3 | 6 6 | 2 1 |
| 10 | 10 | 10 | 8 |
55-65 | 60 |
|
|
|
|
| 4 2 | 16 4 | 12 2 | 8 | 16 | 32 | 32 |
65-75 | 70 |
|
|
|
|
|
| 6 1 | 18 2 | 3 | 9 | 27 | 24 |
Total f | 3 | 17 | 14 | 9 | 6 | 4 | 53 = n | 16 | 92 | 86 | |||
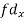 | -6 | -17 | 0 | 9 | 12 | 12 | 10 | Thick figures in small sqs. For 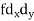 Check: 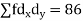 From both sides | |||||
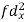 | 12 | 17 | 0 | 9 | 24 | 36 | 98 | ||||||
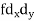 | 8 | 14 | 0 | 10 | 24 | 30 | 86 | ||||||
With the help of the above correlation table, we have