Unit - 3

Concurrency and Synchronization

Q1) Describe process synchronization?

A1) Process Synchronization is the task of coordinating the execution of processes in a way that no two processes can have access to the same shared data and resources.

It is specially needed in a multi-process system when multiple processes are running together, and more than one processes try to gain access to the same shared resource or data at the same time.

This can lead to the inconsistency of shared data. So the change made by one process not necessarily reflected when other processes accessed the same shared data. To avoid this type of inconsistency of data, the processes need to be synchronized with each other.

How Process Synchronization Works?

For Example, process A changing the data in a memory location while another process B is trying to read the data from the same memory location. There is a high probability that data read by the second process will be erroneous.

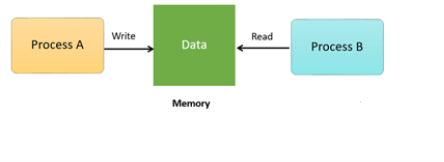
Fig 1: Memory

Sections of a Program

Here, are four essential elements of the critical section:

●        Entry Section: It is part of the process which decides the entry of a particular process.

●        Critical Section: This part allows one process to enter and modify the shared variable.

●        Exit Section: Exit section allows the other process that are waiting in the Entry Section, to enter into the Critical Sections. It also checks that a process that finished its execution should be removed through this Section.

●        Remainder Section: All other parts of the Code, which is not in Critical, Entry, and Exit Section, are known as the Remainder Section.

Q2) What is the critical section problem?

A2) The critical Section is the part of a program that tries to access shared resources. That resource is also any resource in a very pc sort of a memory location, organization, computer hardware, or any IO device.

The vital section can not be dead by quite one method at an identical time; software faces difficulties in permitting and disallowing the processes from coming into the vital section.

The vital section downside is employed to style a group of protocols which might make sure that the Race condition among the processes can ne'er arise.

To synchronize the cooperative processes, our main task is to resolve the vital section downside. We want to supply an answer in such a way that the subsequent conditions are glad.

Requirements of Synchronization mechanisms

Fig 2 - Synchronization mechanisms

1. Progress

Progress means that if one process doesn't need to execute into a critical section then it should not stop other processes to get into the critical section.

2.     Bounded Waiting

We should be able to predict the waiting time for every process to get into the critical section. The process must not be endlessly waiting for getting into the critical section.

3.     Architectural Neutrality

Our mechanism must be architectural natural. It means that if our solution is working fine on one architecture then it should also run on the other ones as well.

Q3) Define semaphore?

A3) Semaphores are integer variables that are utilized to provide solution to the critical section problem.

A semaphore is represented by S and apart from initialization it is utilize by two atomic operations, wait( ) and signal( ) for process synchronization.

Wait( ): The wait operation decreases the value of S, in case it is positive. On the other hand in case S is negative or zero, at that point no activity is performed.

Wait(S)

{

While (S<=0);

S- - ;

}

Signal( ): The signal( ) operation increases the value of its semaphore S.

Signal(S)

{

S++;

}

All changes to the integer value of the semaphore in the wait () and signal() function must be executed individually. That is, the point at which one process adjusts the semaphore value, no other process can at the same time change that equivalent semaphore value.

Furthermore, on account of wait (S), the testing of the integer value of (S ≤ 0), with its conceivable adjustment (S- - ), must be executed without interruption.

Q4) Write the properties of semaphore?

A4) Properties of Semaphores

●        It's basic and consistently have a non-negative integer value.

●        Works with numerous processes.

●        Can have a wide range of critical section with various semaphores.

●        Each critical section has exceptional access semaphores.

●        Can allow numerous processes into the critical section at the same time, if desirable.

Q5) What are the types of semaphore?

A5) Types of Semaphores

There are two primary categories of semaphores for example counting semaphores and binary semaphores. Insights regarding these are given as below:

1. Counting Semaphores: These are integer number value semaphores and have an unlimited value space. These semaphores are utilized to facilitate the resource access, where the semaphore count is the quantity of accessible resources. On the off chance that the resources are added, semaphore count naturally increases and if the resources are removed, the count is decremented.
2. Binary Semaphores: The binary semaphores resemble counting semaphores yet their value is limited to 0 and 1. The wait( ) function possibly works when the semaphore is 1 and the signal operation succeeds when semaphore is 0. It is sometimes simpler to execute binary semaphores than counting semaphores.

Q6) Write the usage of semaphore?

A6) Semaphore Usage

●        In practice, semaphores can take on one of two structures:

●        Binary semaphores can have one of the two values, 0 or 1. They can be utilized to provide solution to the critical section problem as portrayed above, and can be utilized as mutexes on systems that don't give a different mutex mechanism. The utilization of mutexes for this reason is given in figure below.

Do {

Waiting (mutex);

// critical section

Signal (mutex);

//remainder section

} while (true);

Mutual-exclusion usage with semaphores

●        Counting semaphores can take on any integer value, and are generally used to count the remaining number of some resource. The counter is defined to the value of such resources available in the system, and at point the counting semaphore is more than zero, at that point a process can enter a critical section and utilize one of the resources. When the counter gets up to zero (or negative in certain executions), then the process obstructs another process free a resource and increase the counting semaphore with a signal call.

Semaphores can likewise be utilized to synchronize certain tasks between processes. For instance, assume it is significant that process P1 execute instruction S1 before process P2 executes instruction S2.

●        First we make a semaphore named sync that is shared by the two processes, and defined it to zero.

●        At that point in process P1 we embed the code:

S1;

Signal( sync );

●        And in process P2 we embed the code:

Wait( sync );

S2;

●        Since sync was initialized to 0, process P2 will block on the wait until P1 executes the call to signal.

Q7) What are the advantages and disadvantages of semaphore?

A7) Advantages of Semaphores

Some of the benefits of semaphores are as per the following:

1. Semaphores permit just one process into the critical section. They follow the mutual exclusion standard carefully and are substantially more effective than some different techniques for synchronization.
2. There is no resource wastage in view of busy waiting in semaphores as processor time isn't wasted pointlessly to check if a condition is satisfied to enable a process to get to the critical section.
3. Semaphores are implemented in the machine independent code of the microkernel. So they are machine independent.

Disadvantages of Semaphores

Some of the disadvantages of semaphores are as per the following:

1. Semaphores are complicated so the wait and signal function must be designed in the right order to avoid deadlocks.
2. Semaphores are unfeasible for last scale use as their utilization prompts loss of modularity. This happens in light of the fact that the wait and signal tasks avoid the formation of an organized design for the system.
3. Semaphores may prompt a priority inversion where low priority processes may access the critical section first and high priority processes later.

Q8) Explain reader writer problem?

A8) The readers-writers problem is a classical problem of process synchronization, it relates to a data set such as a file that is shared between more than one process at a time. Among these various processes, some are Readers - which can only read the data set; they do not perform any updates, some are Writers - can both read and write in the data sets.

The readers-writers problem is used for managing synchronization among various reader and writer process so that there are no problems with the data sets, i.e. no inconsistency is generated.

Let's understand with an example - If two or more than two readers want to access the file at the same point in time there will be no problem. However, in other situations like when two writers or one reader and one writer wants to access the file at the same point of time, there may occur some problems, hence the task is to design the code in such a manner that if one reader is reading then no writer is allowed to update at the same point of time, similarly, if one writer is writing no reader is allowed to read the file at that point of time and if one writer is updating a file other writers should not be allowed to update the file at the same point of time. However, multiple readers can access the object at the same time.

Let us understand the possibility of reading and writing with the table given below:

TABLE 1

The solution of readers and writers can be implemented using binary semaphores.

We use two binary semaphores "write" and "mutex", where binary semaphore can be defined as:

Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:

1. Wait(S)  
2. {  
3. While(S <= 0) ;  
4. S--;  
5. }  
6.  
7. 2. signal(S)  
8. {  
9. S++;  
10. }  

From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop (because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.

The below code will provide the solution of the reader-writer problem, reader and writer process codes are given as follows -

Code for Reader Process

The code of the reader process is given below -

1. Static int readcount = 0;  
2. Wait (mutex);  
3. Readcount ++; // on each entry of reader increment readcount  
4. If (readcount == 1)  
5. {  
6.  Wait (write);  
7. }  
8. Signal(mutex);  
9.  
10. --READ THE FILE?  
11.  
12. Wait(mutex);  
13. Readcount --; // on every exit of reader decrement readcount  
14. If (readcount == 0)  
15. {  
16.  Signal (write);  
17. }  
18. Signal(mutex);  

In the above code of reader, mutex and write are semaphores that have an initial value of 1, whereas the read count variable has an initial value as 0. Both mutex and write are common in reader and writer process code, semaphore mutex ensures mutual exclusion and semaphore write handles the writing mechanism.

The read count variable denotes the number of readers accessing the file concurrently.

The moment variable read count becomes 1, wait operation is used to write semaphore which decreases the value by one. This means that a writer is not allowed how to access the file anymore. On completion of the read operation, read count is decremented by one. When read count becomes 0, the signal operation which is used to write permits a writer to access the file.

Code for Writer Process

The code that defines the writer process is given below:

1. Wait(write);  
2. WRITE INTO THE FILE  
3. Signal(wrt);  

If a writer wishes to access the file, wait operation is performed on write semaphore, which decrements write to 0 and no other writer can access the file. On completion of the writing job by the writer who was accessing the file, the signal operation is performed on write.

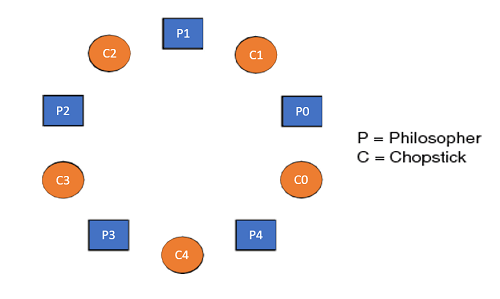
Q9) Describe the dining philosopher problem?

A9) The dining philosopher's problem is the classical problem of synchronization which says that Five philosophers are sitting around a circular table and their job is to think and eat alternatively. A bowl of noodles is placed at the center of the table along with five chopsticks for each of the philosophers. To eat a philosopher needs both their right and a left chopstick. A philosopher can only eat if both immediate left and right chopsticks of the philosopher is available. In case if both immediate left and right chopsticks of the philosopher are not available then the philosopher puts down their (either left or right) chopstick and starts thinking again.

The dining philosopher demonstrates a large class of concurrency control problems hence it's a classic synchronization problem.

Fig 3 - Five Philosophers sitting around the table

Dining Philosophers Problem- Let's understand the Dining Philosophers Problem with the below code, we have used fig 1 as a reference to make you understand the problem exactly. The five Philosophers are represented as P0, P1, P2, P3, and P4 and five chopsticks by C0, C1, C2, C3, and C4.

1. Void Philosopher  
2. {  
3. While(1)  
4.  {  
5.   Take_chopstick[i];  
6.   Take_chopstick[ (i+1) % 5] ;  
7.   . .  
8.   . EATING THE NOODLE  
9.   .  
10.   Put_chopstick[i] );  
11.   Put_chopstick[ (i+1) % 5] ;  
12.   .  
13.   . THINKING  
14.  }  
15. }  

Let's discuss the above code:

Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute take_chopstick[i]; by doing this it holds C0 chopstick after that it execute take_chopstick[ (i+1) % 5]; by doing this it holds C1 chopstick( since i =0, therefore (0 + 1) % 5 = 1)

Similarly suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute take_chopstick[i]; by doing this it holds C1 chopstick after that it execute take_chopstick[ (i+1) % 5]; by doing this it holds C2 chopstick( since i =1, therefore (1 + 1) % 5 = 2)

But Practically Chopstick C1 is not available as it has already been taken by philosopher P0, hence the above code generates problems and produces race condition.

Q10) What is the solution for dining philosopher problem?

A10) The solution of the Dining Philosophers Problem

We use a semaphore to represent a chopstick and this truly acts as a solution of the Dining Philosophers Problem. Wait and Signal operations will be used for the solution of the Dining Philosophers Problem, for picking a chopstick wait operation can be executed while for releasing a chopstick signal semaphore can be executed.

Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:

1. 1. wait(S)  
2. {  
3. While( S <= 0) ;  
4. S--;  
5. }  
6.  
7. 2. signal(S)  
8. {  
9. S++;  
10. }  

From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop (because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.

The structure of the chopstick is an array of a semaphore which is represented as shown below -

1. Semaphore C[5];  

Initially, each element of the semaphore C0, C1, C2, C3, and C4 are initialized to 1 as the chopsticks are on the table and not picked up by any of the philosophers.

Let's modify the above code of the Dining Philosopher Problem by using semaphore operations wait and signal, the desired code looks like

1. Void Philosopher  
2. {  
3. While(1)  
4.  {  
5.   Wait( take_chopstickC[i] );  
6.   Wait( take_chopstickC[(i+1) % 5] ) ;  
7.   . .  
8.   . EATING THE NOODLE  
9.   .  
10.   Signal( put_chopstickC[i] );  
11.   Signal( put_chopstickC[ (i+1) % 5] ) ;  
12.   .  
13.   . THINKING  
14.  }  
15. }  

In the above code, first wait operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows philosopher i have picked up the chopsticks from its left and right. The eating function is performed after that.

On completion of eating by philosopher i the, signal operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows that the philosopher i have eaten and put down both the left and right chopsticks. Finally, the philosopher starts thinking again.

Let's understand how the above code is giving a solution to the dining philosopher problem?

Let value of i = 0( initial value ), Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it holds C0 chopstick and reduces semaphore C0 to 0, after that it execute Wait( take_chopstickC[(i+1) % 5] ); by doing this it holds C1 chopstick( since i =0, therefore (0 + 1) % 5 = 1) and reduces semaphore C1 to 0

Similarly, suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it will try to hold C1 chopstick but will not be able to do that, since the value of semaphore C1 has already been set to 0 by philosopher P0, therefore it will enter into an infinite loop because of which philosopher P1 will not be able to pick chopstick C1 whereas if Philosopher P2 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it holds C2 chopstick and reduces semaphore C2 to 0, after that, it executes Wait( take_chopstickC[(i+1) % 5] ); by doing this it holds C3 chopstick( since i =2, therefore (2 + 1) % 5 = 3) and reduces semaphore C3 to 0.

Hence the above code is providing a solution to the dining philosopher problem, A philosopher can only eat if both immediate left and right chopsticks of the philosopher are available else philosopher needs to wait. Also at one go two independent philosophers can eat simultaneously (i.e., philosopher P0 and P2, P1 and P3 & P2 and P4 can eat simultaneously as all are the independent processes and they are following the above constraint of dining philosopher problem)

Q11) Explain the sleeping barber problem?

A11) Problem: The analogy is predicated upon a theoretical barber look with one barber. There's a barber look that has one barber, one chair, and n chairs for waiting for patrons if there are any to sit down on the chair.

• If there's no client, then the barber sleeps in his chair.

• When a client arrives, he has got to awaken the barber.

• If there are many purchasers and therefore the barber is cutting a customer’s hair, then the remaining customers either wait if their ar empty chairs within the {waiting room|lounge|waiting ara|room} or they leave if no chairs are empty.

Fig 4 - Example

Solution: the answer to the current downside includes 3 semaphores. First is for the customer that counts the quantity of consumers' gift within the room (customer within the chair isn't enclosed as a result of he's not waiting). Second, the barber zero or one is employed to inform whether or not the barber is idle or is functioning, and therefore the third mutex is employed to supply the mutual exclusion that is needed for the method to execute. Within the solution, the client has the record of the quantity {of clients|of consumers|of shoppers} waiting within the room if the quantity of consumers is adequate to the number of chairs within the room then the approaching customer leaves the store.

When the barber shows up within the morning, he executes the procedure barber, inflicting him to the dam on the semaphore customers as a result of it's at the start zero. Then the barber goes to sleep till the primary client comes up.

When a client arrives, he executes the client procedure the client acquires the mutex for coming into the crucial region, if another client enters thenceforth, the other won't be able to something till the primary one has free the mutex. The client then checks the chairs within the {waiting room|lounge|waiting ara|room} if waiting customers are less then the number of chairs then he sits otherwise he leaves and releases the mutex.

If the chair is accessible then the client sits within the room and increments the variable waiting price and additionally will increase the customer’s semaphore this wakes up the barber if he's sleeping.

At now, the client and barber are each awake, and therefore the barber is prepared to relinquish that person a haircut. Once the haircut is over, the client exits the procedure, and if there aren't any customers in the room barber sleeps.

Fig 5 - Example

Algorithm for Sleeping Barber problem:

Q12) What is the solution for the critical section problem?

A12) The following are some typical critical section solutions:

​​1. Peterson Solution:  When a process is in a critical condition, the other process can only run the remaining code, and vice versa.

This strategy, created by Peterson, is commonly used to ensure that only one process in the critical region operates at any one moment.

Let's say there are N processes (P1, P2,... PN), and each of them must enter the Critical Section at some point. The default value of the FLAG[] array of size N is false. As a result, if a process wishes to reach the crucial area, its flag must be set to true.

The process number waiting to enter the Critical Section is indicated by the variable TURN. When a process exits the crucial section, it changes the TURN to a different number from the list of ready processes.

Program

PROCESS Pi

FLAG[i] = true

While( (turn != i) AND (CS is !free) ){ wait;

}

CRITICAL SECTION FLAG[i] = false

Turn = j; //choose another process

2. Synchronization Hardware: Hardware can occasionally assist in the resolution of crucial section issues. Some operating systems provide a lock feature. When a process enters a crucial section, it is given a lock, which it must release when it exits the critical area. As a result, other processes are unable to access a crucial area if one is already present.

3. Mutex Locks: Mutex Locks are a stringent software approach in which a process is handed a LOCK over critical resources in the entering section of code. This LOCK can be used in the critical phase of the procedure and then removed in the exit section.

4. Semaphore Solution: Semaphore is a shared non-negative variable between threads. It's a signaling system that uses a thread waiting on a semaphore to send a message to another thread. For process synchronization, it uses wait and signal.

Example

WAIT ( S );

While ( S <= 0 );

S = S - 1;

SIGNAL ( S ):

S = S + 1;